人教版八年级数学上册《因式分解-公式法》第2课时 课件(共31张PPT)
文档属性
| 名称 | 人教版八年级数学上册《因式分解-公式法》第2课时 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 21:36:36 | ||
图片预览









文档简介
(共31张PPT)
因式分解——公式法
(第二课时)
复习引入
请你根据所学知识将下面的多项式分解因式:
1
2
因式分解的一般步骤是什么?
问题
有公因式先提公因式,再检查是否可用平方差公式.
复习引入
请你根据所学知识将下面的多项式分解因式:
1
2
因式分解的平方差公式与整式乘法的平方差公式有什么关系
问题
方向相反的等式变形.
复习引入
请你根据所学知识将下面的多项式分解因式:
1
2
除了平方差公式我们还学过其他乘法公式吗?
问题
乘法公式中的完全平方公式:
,
,
因式分解中的完全平方公式:
探究新知
观察多项式:
,
1
共有几项?
2
这三项有什么特点?
三项.
有两项是两数的平方和,一项为这两数乘积的 倍.
归纳
我们把 与 这样的式子叫做完全平方式.
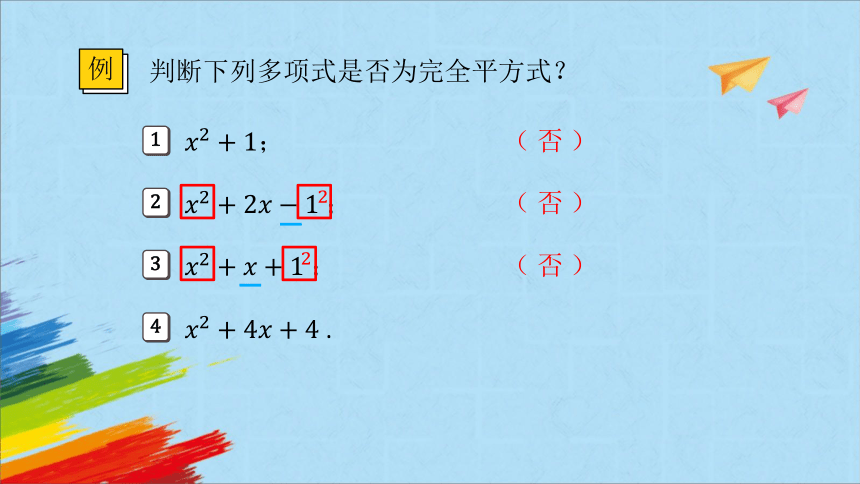
判断下列多项式是否为完全平方式?
例
1
;
2
;
3
;
4
.
( 否 )
( 否 )
( 否 )
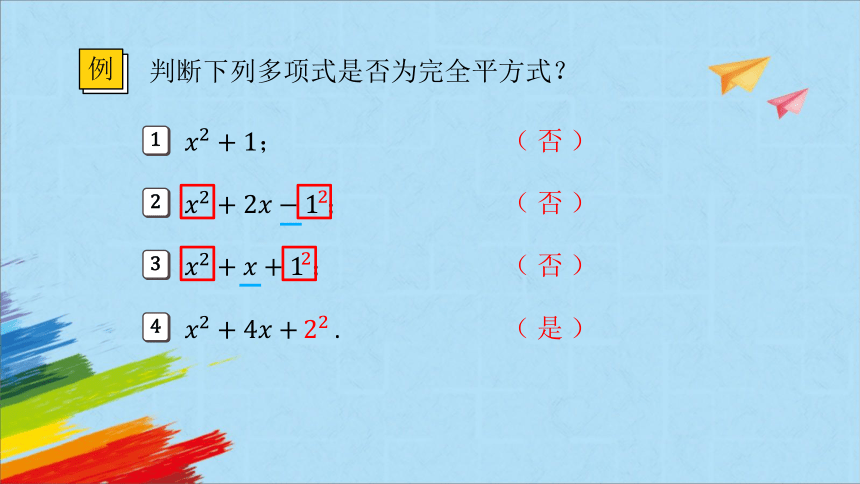
判断下列多项式是否为完全平方式?
例
1
;
2
;
3
;
4
.
( 否 )
( 否 )
( 否 )
( 是 )
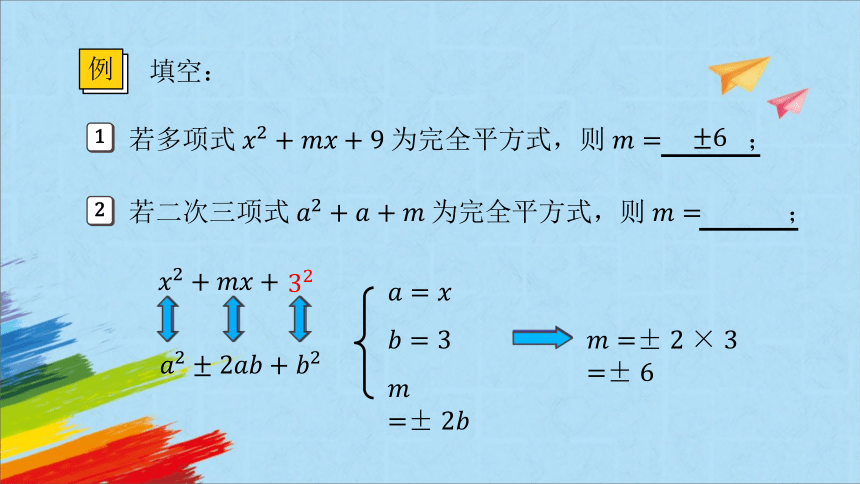
填空:
例
1
2
若多项式 为完全平方式,则 ;
若二次三项式 为完全平方式,则 ;
填空:
例
1
2
若多项式 为完全平方式,则 ;
若二次三项式 为完全平方式,则 ;
填空:
例
1
2
若多项式 为完全平方式,则 ;
若二次三项式 为完全平方式,则 ;
归纳
完全平方式:
符号表示: ;
文字表述:
两数的平方和加上(或减去)这两数乘积的 倍.
探究新知
你能将完全平方式 和 分解因式吗?
,
即:
两个数的平方和加上(或减去)这两个数的积的 倍,等于这两个数的和(或差)的平方.
分解因式:
例
1
分析
,
,
,
所以 是一个完全平方式,即
;
分解因式:
例
1
;
解:
原式
分解因式:
例
2
;
解:
原式
分解因式:
例
3
.
解:
原式
归纳
1
2
利用完全平方公式因式分解的关键是识别完全平方式;
多项式分解因式时要先观察是否有公因式,有公因式要先提公因式,再判断多项式因式是否可以继续分解.
先找某两数平方和
再验证两数积的 倍
利用完全平方公式因式分解
利用简便方法计算.
例
利用简便方法计算.
例
解:
原式
巩固练习
分解因式:
1
1
;
2
3
.
解:
1
巩固练习
分解因式:
1
1
;
2
3
.
解:
2
巩固练习
分解因式:
1
1
;
2
3
.
解:
3
巩固练习
在括号中填入适当的式子,使等式成立:
2
1
;
等号左边为完全平方式:
巩固练习
在括号中填入适当的式子,使等式成立:
2
2
.
等号左边为完全平方式:
,,
.
巩固练习
计算:
3
.
解:
知识拓展
若 , 为任意实数,且 ,,则 , 的大小关系是 .
, 为任意实数,
.
.
解:
.
课
堂
小
结
完全平方式:
1
利用完全平方公式因式分解:
2
形如 的式子是完全平方式;
课后作业
下列多项式是不是完全平方式?为什么?
1
1
;
2
;
3
;
4
.
课后作业
因式分解:
2
1
;
2
;
3
;
4
5
.
因式分解——公式法
(第二课时)
复习引入
请你根据所学知识将下面的多项式分解因式:
1
2
因式分解的一般步骤是什么?
问题
有公因式先提公因式,再检查是否可用平方差公式.
复习引入
请你根据所学知识将下面的多项式分解因式:
1
2
因式分解的平方差公式与整式乘法的平方差公式有什么关系
问题
方向相反的等式变形.
复习引入
请你根据所学知识将下面的多项式分解因式:
1
2
除了平方差公式我们还学过其他乘法公式吗?
问题
乘法公式中的完全平方公式:
,
,
因式分解中的完全平方公式:
探究新知
观察多项式:
,
1
共有几项?
2
这三项有什么特点?
三项.
有两项是两数的平方和,一项为这两数乘积的 倍.
归纳
我们把 与 这样的式子叫做完全平方式.
判断下列多项式是否为完全平方式?
例
1
;
2
;
3
;
4
.
( 否 )
( 否 )
( 否 )
判断下列多项式是否为完全平方式?
例
1
;
2
;
3
;
4
.
( 否 )
( 否 )
( 否 )
( 是 )
填空:
例
1
2
若多项式 为完全平方式,则 ;
若二次三项式 为完全平方式,则 ;
填空:
例
1
2
若多项式 为完全平方式,则 ;
若二次三项式 为完全平方式,则 ;
填空:
例
1
2
若多项式 为完全平方式,则 ;
若二次三项式 为完全平方式,则 ;
归纳
完全平方式:
符号表示: ;
文字表述:
两数的平方和加上(或减去)这两数乘积的 倍.
探究新知
你能将完全平方式 和 分解因式吗?
,
即:
两个数的平方和加上(或减去)这两个数的积的 倍,等于这两个数的和(或差)的平方.
分解因式:
例
1
分析
,
,
,
所以 是一个完全平方式,即
;
分解因式:
例
1
;
解:
原式
分解因式:
例
2
;
解:
原式
分解因式:
例
3
.
解:
原式
归纳
1
2
利用完全平方公式因式分解的关键是识别完全平方式;
多项式分解因式时要先观察是否有公因式,有公因式要先提公因式,再判断多项式因式是否可以继续分解.
先找某两数平方和
再验证两数积的 倍
利用完全平方公式因式分解
利用简便方法计算.
例
利用简便方法计算.
例
解:
原式
巩固练习
分解因式:
1
1
;
2
3
.
解:
1
巩固练习
分解因式:
1
1
;
2
3
.
解:
2
巩固练习
分解因式:
1
1
;
2
3
.
解:
3
巩固练习
在括号中填入适当的式子,使等式成立:
2
1
;
等号左边为完全平方式:
巩固练习
在括号中填入适当的式子,使等式成立:
2
2
.
等号左边为完全平方式:
,,
.
巩固练习
计算:
3
.
解:
知识拓展
若 , 为任意实数,且 ,,则 , 的大小关系是 .
, 为任意实数,
.
.
解:
.
课
堂
小
结
完全平方式:
1
利用完全平方公式因式分解:
2
形如 的式子是完全平方式;
课后作业
下列多项式是不是完全平方式?为什么?
1
1
;
2
;
3
;
4
.
课后作业
因式分解:
2
1
;
2
;
3
;
4
5
.
