人教版八年级数学上册《因式分解-公式法》第1课时 课件(共32张PPT)
文档属性
| 名称 | 人教版八年级数学上册《因式分解-公式法》第1课时 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 21:40:38 | ||
图片预览










文档简介
(共32张PPT)
因式分解——公式法
(第一课时)
复习引入
把一个多项式化成几个整式的积的形式,这样的变形叫做因式分解.
什么叫做因式分解?
问题
我们已学习过什么因式分解的方法?
问题
提公因式法.
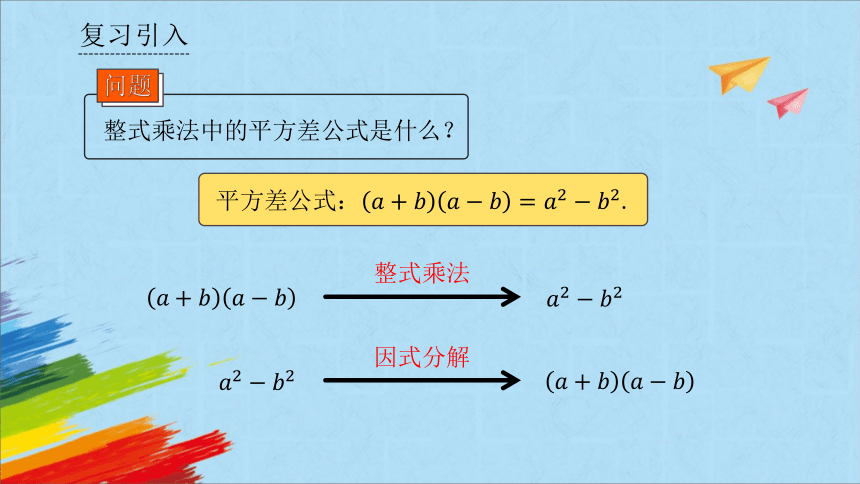
复习引入
平方差公式:.
整式乘法中的平方差公式是什么?
问题
整式乘法
因式分解
探究新知
这样我们就得到了 因式分解的方法:
两个数的平方差,等于这两个数的和与这两个数的差的积.
利用平方差公式法因式分解时,多项式需具备什么特点?
探究新知
公式左边:
1
多项式有两项;
2
这两项异号;
3
两项是平方差.
公式右边:
两个数的和与这两个数的差的乘积的形式.
1
2
3
判断下列各式能否用平方差公式因式分解:
练习
4
5
6
原式
原式
1
分解因式:
例
2
1
分解因式:
例
解:
原式
分解因式:
例
2
设:,
即:
分解因式:
例
2
原式
解:
A
B
D
下列因式分解错误的是( )
练习
C
分析
分析
A
B
D
C
下列因式分解错误的是( )
练习
分析
A
B
D
C
下列因式分解错误的是( )
练习
分析
A
B
D
C
下列因式分解错误的是( )
练习
1
分解因式:
例
2
1
分解因式:
例
解:
原式
还可以继续分解!
此时,因式分解彻底了吗?
分解因式:
例
解:
原式
有公因式
2
因式分解的步骤
1
若多项式中有公因式,应先提取公因式,再进一步分解因式;
2
剩余因式若有两项,异号,两项是平方差,则用平方差公式继续分解因式.
注意
每个因式要分解到不能继续分解为止.
分解因式:
练习
1
2
3
4
分解因式:
练习
1
解:
原式
原式
分解因式:
练习
解:
原式
2
分解因式:
练习
解:
原式
可以继续分解
3
分解因式:
练习
解:
原式
4
1
利用因式分解计算:
例
2
1
利用因式分解计算:
例
可用平方差公式分解
解:
原式
利用因式分解计算:
例
先提取公因数
解:
原式
2
如图,在一块长为 的正方形纸片的四角,各减去一个边长为 的正方形,求剩余部分面积是多少?若 ,,求剩余部分面积.
例
解:
把 带入:
剩
剩
答:剩余部分面积为 .
想一想:我们今天学习了哪些知识?
课
堂
小
结
利用平方差公式分解因式:
1
1
多项式有两项;
2
这两项异号;
3
两项是平方差.
两个数的和与这两个数的差的乘积.
注意
公式中的字母 , 可以表示数、单项式或多项式.
课
堂
小
结
利用平方差公式分解因式步骤:
2
1
若多项式中有公因式,应先提取公因式,再进一步分解因式;
2
剩余因式若有两项,异号,两项是平方差,则用平方差公式继续分解因式.
拓展提升
如图, 个正方形由小到大套在一起,从外向里相间画上阴影,最里面一个小正方形没有画阴影,最外面一层画阴影,最外面的正方形的边长为 ,向里依次为 ,,..., ,那么在这个图形中,所有画阴影部分的面积和是多少?
解:
阴影
答:阴影部分的面积和为
课后作业
下列各式能否用平方差公式分解因式?为什么?
1
1
2
3
4
1
2
3
4
分解因式:
2
已知 ,,
求 的值和 , 的值.
3
因式分解——公式法
(第一课时)
复习引入
把一个多项式化成几个整式的积的形式,这样的变形叫做因式分解.
什么叫做因式分解?
问题
我们已学习过什么因式分解的方法?
问题
提公因式法.
复习引入
平方差公式:.
整式乘法中的平方差公式是什么?
问题
整式乘法
因式分解
探究新知
这样我们就得到了 因式分解的方法:
两个数的平方差,等于这两个数的和与这两个数的差的积.
利用平方差公式法因式分解时,多项式需具备什么特点?
探究新知
公式左边:
1
多项式有两项;
2
这两项异号;
3
两项是平方差.
公式右边:
两个数的和与这两个数的差的乘积的形式.
1
2
3
判断下列各式能否用平方差公式因式分解:
练习
4
5
6
原式
原式
1
分解因式:
例
2
1
分解因式:
例
解:
原式
分解因式:
例
2
设:,
即:
分解因式:
例
2
原式
解:
A
B
D
下列因式分解错误的是( )
练习
C
分析
分析
A
B
D
C
下列因式分解错误的是( )
练习
分析
A
B
D
C
下列因式分解错误的是( )
练习
分析
A
B
D
C
下列因式分解错误的是( )
练习
1
分解因式:
例
2
1
分解因式:
例
解:
原式
还可以继续分解!
此时,因式分解彻底了吗?
分解因式:
例
解:
原式
有公因式
2
因式分解的步骤
1
若多项式中有公因式,应先提取公因式,再进一步分解因式;
2
剩余因式若有两项,异号,两项是平方差,则用平方差公式继续分解因式.
注意
每个因式要分解到不能继续分解为止.
分解因式:
练习
1
2
3
4
分解因式:
练习
1
解:
原式
原式
分解因式:
练习
解:
原式
2
分解因式:
练习
解:
原式
可以继续分解
3
分解因式:
练习
解:
原式
4
1
利用因式分解计算:
例
2
1
利用因式分解计算:
例
可用平方差公式分解
解:
原式
利用因式分解计算:
例
先提取公因数
解:
原式
2
如图,在一块长为 的正方形纸片的四角,各减去一个边长为 的正方形,求剩余部分面积是多少?若 ,,求剩余部分面积.
例
解:
把 带入:
剩
剩
答:剩余部分面积为 .
想一想:我们今天学习了哪些知识?
课
堂
小
结
利用平方差公式分解因式:
1
1
多项式有两项;
2
这两项异号;
3
两项是平方差.
两个数的和与这两个数的差的乘积.
注意
公式中的字母 , 可以表示数、单项式或多项式.
课
堂
小
结
利用平方差公式分解因式步骤:
2
1
若多项式中有公因式,应先提取公因式,再进一步分解因式;
2
剩余因式若有两项,异号,两项是平方差,则用平方差公式继续分解因式.
拓展提升
如图, 个正方形由小到大套在一起,从外向里相间画上阴影,最里面一个小正方形没有画阴影,最外面一层画阴影,最外面的正方形的边长为 ,向里依次为 ,,..., ,那么在这个图形中,所有画阴影部分的面积和是多少?
解:
阴影
答:阴影部分的面积和为
课后作业
下列各式能否用平方差公式分解因式?为什么?
1
1
2
3
4
1
2
3
4
分解因式:
2
已知 ,,
求 的值和 , 的值.
3
