人教版八年级数学上册13.4最短路径问题(2)教学课件(共23张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.4最短路径问题(2)教学课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 20:35:38 | ||
图片预览





文档简介
(共23张PPT)
最短路径问题
(第二课时)
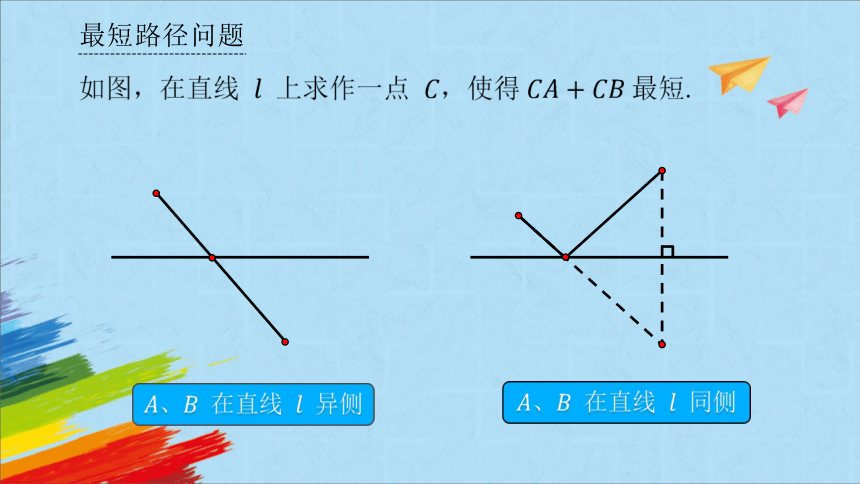
最短路径问题
如图,在直线 上求作一点 ,使得最短.
在直线 异侧
在直线 同侧
例:造桥选址问题
如图, 和 两地在一条河的两岸,现要在河上造一座桥 . 桥造在何处可使从 到 的路径 最短(假定河的两岸是平行的直线,桥要与河垂直)
例
当点 在直线 的什么位置时, 最小?
当点 在直线 的什么位置时, 最小?
思考
问题能否简化?
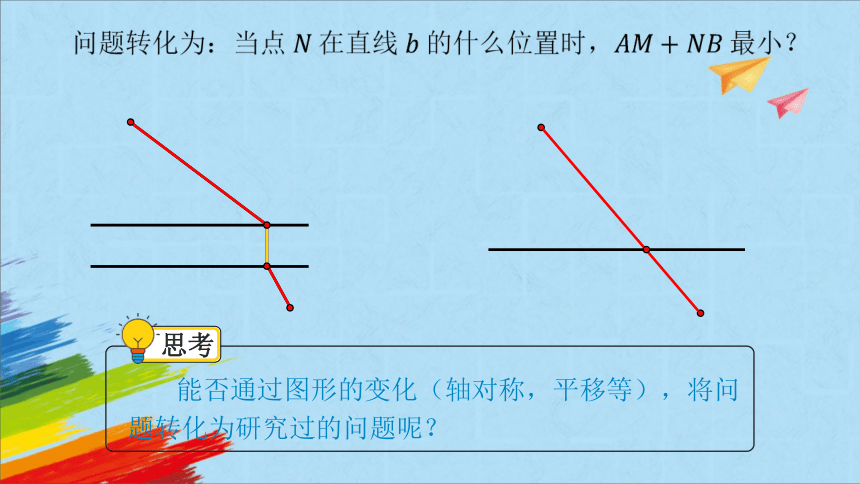
问题转化为:当点 在直线 的什么位置时, 最小?
思考
能否通过图形的变化(轴对称,平移等),将问题转化为研究过的问题呢?
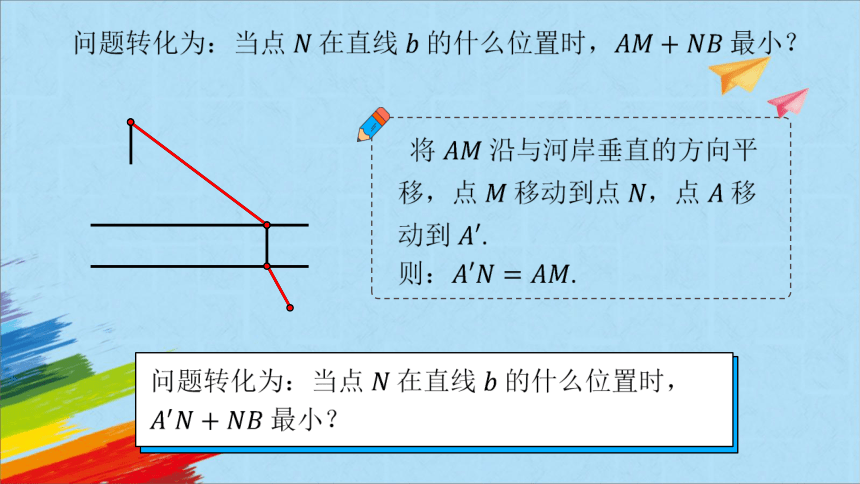
将 沿与河岸垂直的方向平移,点 移动到点 ,点 移动到 .
则:.
问题转化为:当点 在直线 的什么位置时, 最小?
问题转化为:当点 在直线 的什么位置时, 最小?
连接 ,交直线 于点 .点 即为所求.
问题转化为:当点 在直线 的什么位置时, 最小?
作法
将 沿与河岸垂直的方向平移到 ,
使得 的长度等于桥长.
连接 ,交直线 于点 .
点 即为所求.
过 作 于 ,
线段 即为桥的位置.
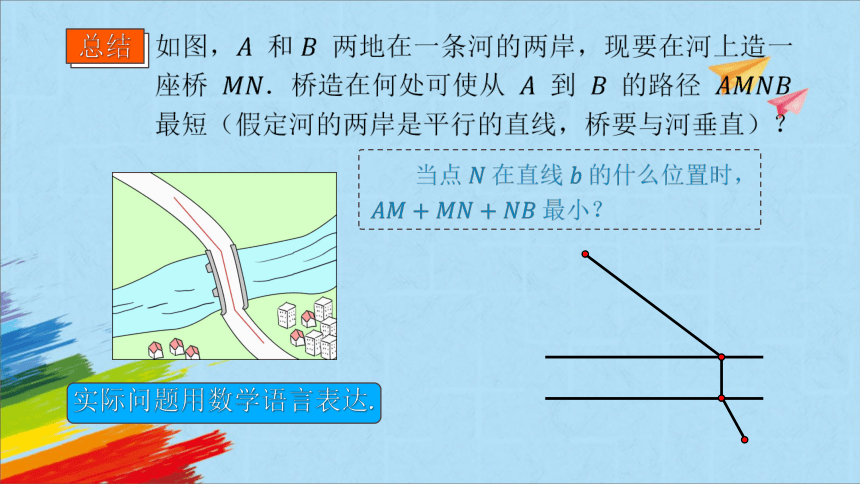
总结
如图, 和 两地在一条河的两岸,现要在河上造一座桥 .桥造在何处可使从 到 的路径 最短(假定河的两岸是平行的直线,桥要与河垂直)?
实际问题用数学语言表达.
当点 在直线 的什么位置时, 最小?
当点 在直线 的什么位置时, 最小?
当点 在直线 的什么位置时, 最小?
总结
利用平移,实现线段的转移.
转化1
当点 在直线 的什么位置时, 最小?
转化2
把已知问题转化成容易解决的问题.
造桥选址问题
实际问题用数学语言表达.
1
2
利用平移,实现线段的转移.
3
把已知问题转化成容易解决的问题.
只需证明:
.
只需证明:
.
如何证明这条路径 最短?
思考
.
只需证明:
由两点之间,线段最短可证.
如何证明这条路径 最短?
思考
在直线 上任取一点 ,过 作 .
即 .
由平移性质可知,,.
连接 ,,.
.
.
由两点之间,线段最短可知:
.
即 .
造桥选址问题
实际问题用数学语言表达.
1
2
利用平移,实现线段的转移.
3
把已知问题转化成容易解决的问题.
4
用符号语言进行推理和表达.
已知线段 ,点 在直线 的同侧,在直线 上求作两点 ,(点 在点 的左侧)且 ,使得四边形 的周长最小.
练习
思考
哪些点是定点?
哪些点是动点?
问题转化为:
当点 在什么位置时, 最小.
问题是否可以简化?
思考
问题转化为:当点 在什么位置时, 最小.
思考
通过哪种图形的变化(轴对称,平移等),可以将问题转化为研究过的问题呢
问题转化为:当点 在什么位置时, 最小.
将 沿直线 的方向平移,点 移动到 ,点 移动到点 .
则:.
问题转化为:
当点 在什么位置时, 最小.
作 关于直线 的对称点 .
连接 ,与直线 交于一点即为所求点 .
在直线 上求作两点 ,,使得四边形 的周长最小.
问题
问题转化为:当点 在什么位置时, 最小.
将点 沿直线 方向平移至 ,使得 .
连接 ,与直线 交于一点即为所求点 .
作法
作 关于直线 的对称点 .
在点 左侧取点 ,
使得 ,即为所求点 .
练习
已知线段 ,点 在直线 的同侧,在直线 上求作两点 ,(点 在点 的左侧)且 ,使得四边形 的周长最小.
练习
思考
你能证明此时四边形 的周长最小吗?
已知线段 ,点 在直线 的同侧,在直线 上求作两点 ,(点 在点 的左侧)且 ,使得四边形 的周长最小.
最短路径问题
造桥选址问题
练习
课
堂
小
结
化归思想.
课
堂
小
结
利用轴对称、平移等变化,把已知问题转化为容易解决的问题.
两点之间,线段最短.
依据
方法
思想
课后作业
点 、、 在直线 的同侧,在直线 上,求作一点 ,使得四边形 的周长最小.
最短路径问题
(第二课时)
最短路径问题
如图,在直线 上求作一点 ,使得最短.
在直线 异侧
在直线 同侧
例:造桥选址问题
如图, 和 两地在一条河的两岸,现要在河上造一座桥 . 桥造在何处可使从 到 的路径 最短(假定河的两岸是平行的直线,桥要与河垂直)
例
当点 在直线 的什么位置时, 最小?
当点 在直线 的什么位置时, 最小?
思考
问题能否简化?
问题转化为:当点 在直线 的什么位置时, 最小?
思考
能否通过图形的变化(轴对称,平移等),将问题转化为研究过的问题呢?
将 沿与河岸垂直的方向平移,点 移动到点 ,点 移动到 .
则:.
问题转化为:当点 在直线 的什么位置时, 最小?
问题转化为:当点 在直线 的什么位置时, 最小?
连接 ,交直线 于点 .点 即为所求.
问题转化为:当点 在直线 的什么位置时, 最小?
作法
将 沿与河岸垂直的方向平移到 ,
使得 的长度等于桥长.
连接 ,交直线 于点 .
点 即为所求.
过 作 于 ,
线段 即为桥的位置.
总结
如图, 和 两地在一条河的两岸,现要在河上造一座桥 .桥造在何处可使从 到 的路径 最短(假定河的两岸是平行的直线,桥要与河垂直)?
实际问题用数学语言表达.
当点 在直线 的什么位置时, 最小?
当点 在直线 的什么位置时, 最小?
当点 在直线 的什么位置时, 最小?
总结
利用平移,实现线段的转移.
转化1
当点 在直线 的什么位置时, 最小?
转化2
把已知问题转化成容易解决的问题.
造桥选址问题
实际问题用数学语言表达.
1
2
利用平移,实现线段的转移.
3
把已知问题转化成容易解决的问题.
只需证明:
.
只需证明:
.
如何证明这条路径 最短?
思考
.
只需证明:
由两点之间,线段最短可证.
如何证明这条路径 最短?
思考
在直线 上任取一点 ,过 作 .
即 .
由平移性质可知,,.
连接 ,,.
.
.
由两点之间,线段最短可知:
.
即 .
造桥选址问题
实际问题用数学语言表达.
1
2
利用平移,实现线段的转移.
3
把已知问题转化成容易解决的问题.
4
用符号语言进行推理和表达.
已知线段 ,点 在直线 的同侧,在直线 上求作两点 ,(点 在点 的左侧)且 ,使得四边形 的周长最小.
练习
思考
哪些点是定点?
哪些点是动点?
问题转化为:
当点 在什么位置时, 最小.
问题是否可以简化?
思考
问题转化为:当点 在什么位置时, 最小.
思考
通过哪种图形的变化(轴对称,平移等),可以将问题转化为研究过的问题呢
问题转化为:当点 在什么位置时, 最小.
将 沿直线 的方向平移,点 移动到 ,点 移动到点 .
则:.
问题转化为:
当点 在什么位置时, 最小.
作 关于直线 的对称点 .
连接 ,与直线 交于一点即为所求点 .
在直线 上求作两点 ,,使得四边形 的周长最小.
问题
问题转化为:当点 在什么位置时, 最小.
将点 沿直线 方向平移至 ,使得 .
连接 ,与直线 交于一点即为所求点 .
作法
作 关于直线 的对称点 .
在点 左侧取点 ,
使得 ,即为所求点 .
练习
已知线段 ,点 在直线 的同侧,在直线 上求作两点 ,(点 在点 的左侧)且 ,使得四边形 的周长最小.
练习
思考
你能证明此时四边形 的周长最小吗?
已知线段 ,点 在直线 的同侧,在直线 上求作两点 ,(点 在点 的左侧)且 ,使得四边形 的周长最小.
最短路径问题
造桥选址问题
练习
课
堂
小
结
化归思想.
课
堂
小
结
利用轴对称、平移等变化,把已知问题转化为容易解决的问题.
两点之间,线段最短.
依据
方法
思想
课后作业
点 、、 在直线 的同侧,在直线 上,求作一点 ,使得四边形 的周长最小.
