人教版八年级数学上册13.4 最短路径问题(1)教学课件(共39张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.4 最短路径问题(1)教学课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 00:00:00 | ||
图片预览




文档简介
(共39张PPT)
最短路径问题
(第一课时)
最值问题
最多
最长
最胖
最少
最短
最瘦
“最短路径问题”
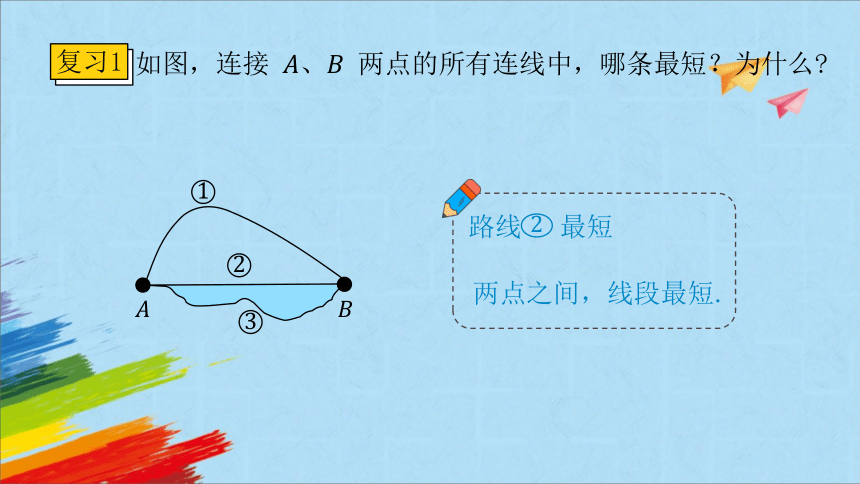
如图,连接 、 两点的所有连线中,哪条最短?为什么
复习1
2
1
3
路线 最短
2
两点之间,线段最短.
点是直线外一点,点 与该直线 上各点连接的所有线段中,哪条最短?为什么?
最短
1
1
1
1
1
1
1
垂线段最短
复习2
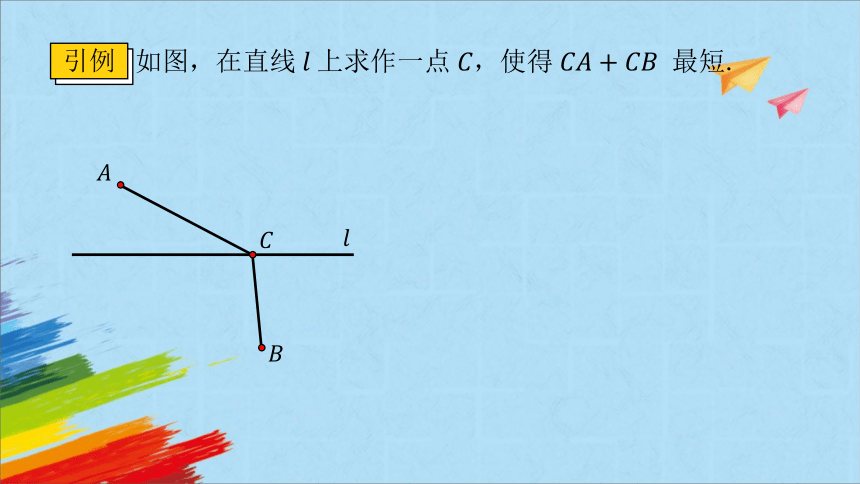
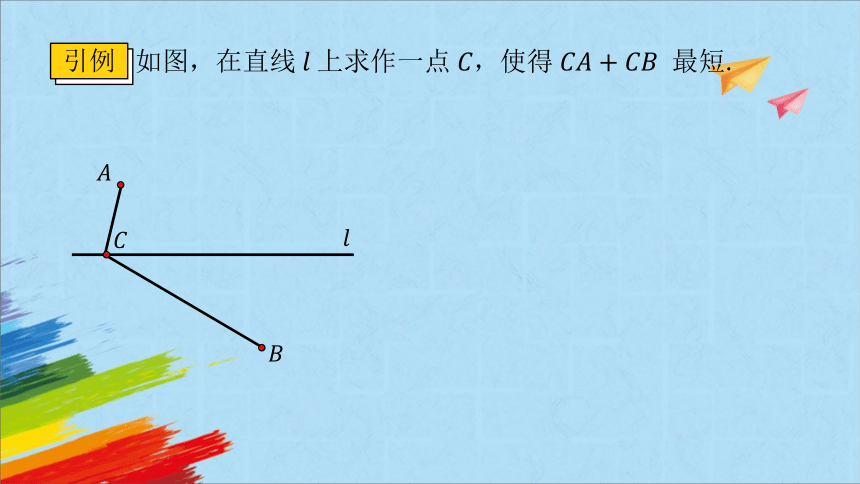
如图,在直线上求作一点,使得 最短.
引例
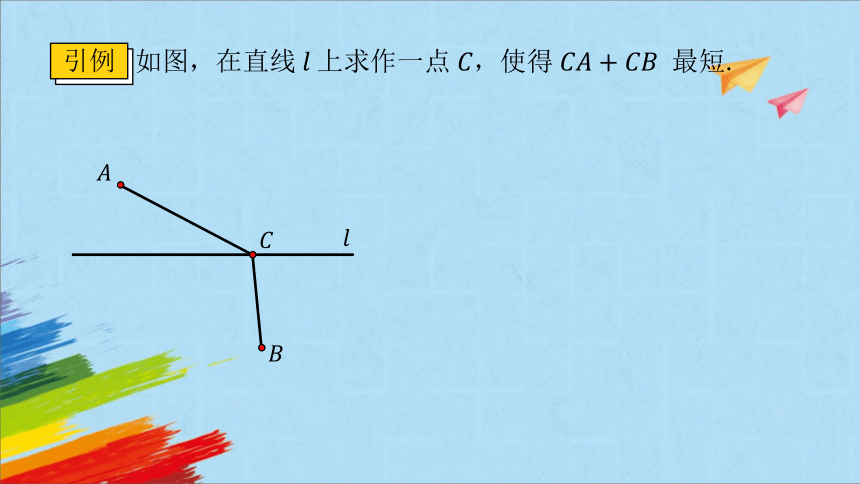
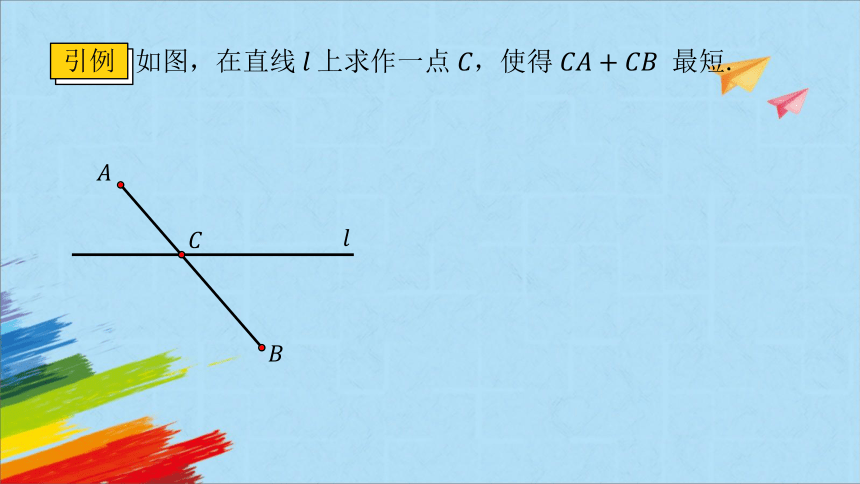
如图,在直线上求作一点,使得 最短.
引例
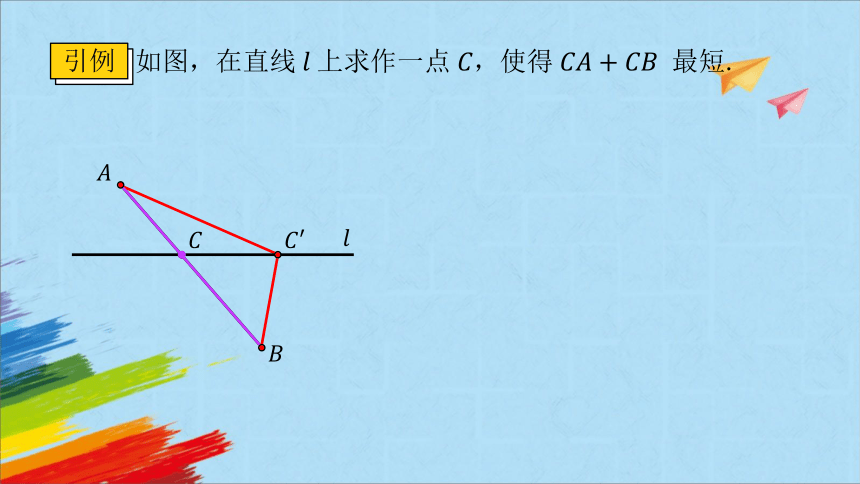
如图,在直线上求作一点,使得 最短.
引例
如图,在直线上求作一点,使得 最短.
引例
如图,在直线上求作一点,使得 最短.
引例
如图,在直线上求作一点,使得 最短.
引例
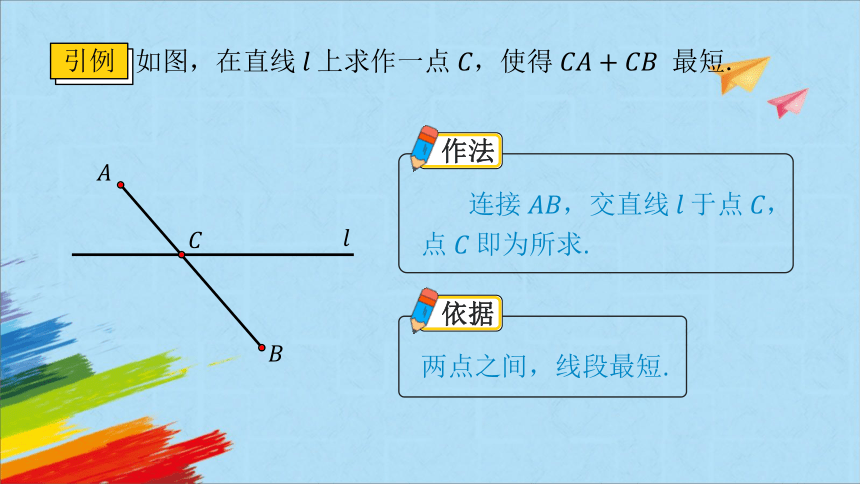
如图,在直线上求作一点,使得 最短.
作法
, .
依据
.
引例
如图,牧马人从地出发,到一条笔直的河边 饮马,然后到 地,牧马人到河边的什么地方饮马,可使所走的路径最短?
例
如图,在直线 上求作一点,使 最短.
文字语言
符号语言
图形语言
如图,在直线 上求作一点,使 最短.
例
如图,在直线 上求作一点,使 最短.
例
如图,在直线 上求作一点,使 最短.
例
如图,在直线 上求作一点,使 最短.
例
如图,在直线 上求作一点,使 最短.
例
如图,在直线 上求作一点,使 最短.
例
如图,在直线 上求作一点,使 最短.
例
在直线 同侧
在直线 异侧
引例
能否通过图形的变化(轴对称、平移等),将问题转化为我们研究过的问题呢
思考
如图,在直线 上求作一点,使 最短.
例
如图,在直线 上求作一点,使 最短.
例
问题转化为:
在直线 上求作一点 使 最短.
如图,在直线 上求作一点,使 最短.
例
作法
;
;
.
如图,在直线 上求作一点,使 最短.
例
思考
证明
,
,.
如图,在直线 上求作一点,使 最短.
例
思考
证明
,
,
,.
如图,牧马人从地出发,到一条笔直的河边 饮马,然后到 地,牧马人到河边的什么地方饮马,可使所走的路径最短?
例
如图,在直线 上求作一点,使 最短.
例
总结
1
将实际问题抽象成数学问题,用数学语言表达.
2
利用轴对称转移线段,将问题转化为研究过的引例:即两点之间,线段最短的问题.
3
用符号语言证明结论.
有两棵树位置如图,树的底部分别为 地上有一只昆虫沿着—的路径在地面上爬行. 小树顶处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶 处. 问小鸟飞至之间何处时,飞行距离最短,在图中画出该点的位置.
练习
,.
,.
作法
;
;
.
,.
作法
;
;
.
有两棵树位置如图,树的底部分别为 地上有一只昆虫沿着—的路径在地面上爬行. 小树顶处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶 处. 问小鸟飞至之间何处时,飞行距离最短,在图中画出该点的位置.
练习
作法
;
;
.
如图,已知点,点 分别是等边三角形 中、 边的中点,,点 是 边上的动点,则 的最小值为 .
例
1
1
1
1
1
如图,已知点,点 分别是等边三角形 中、 边的中点,,点 是 边上的动点,则 的最小值为 .
例
1
1
1
1
1
如图,已知点,点 分别是等边三角形 中、 边的中点,,点 是 边上的动点,则 的最小值为 .
例
利用轴对称转移线段,将问题转化为研究过两点之间,线段最短的问题.
方法
问题
和,作哪个点的对称点更好?
如图,已知点,点 分别是等边三角形 中、 边的中点,,点 是 边上的动点,则 的最小值为 .
例
.
思路
.
.
如图,已知点,点 分别是等边三角形 中、 边的中点,,点 是 边上的动点,则 的最小值为 .
例
.
.
.
思路
,
.
如图,已知点,点 分别是等边三角形 中、 边的中点,,点 是 边上的动点,则 的最小值为 .
例
总结
1
分析题目中的定点和动点,转化为我们熟悉的最短路径问题.
2
利用等边三角形的轴对称性找到合适的对称点.
课
堂
小
结
1
最短路径问题
如图,在直线 上求作一点,使得 最短.
在直线 异侧
在直线 同侧
课
堂
小
结
1
最短路径问题
两点之间,线段最短
依据
利用轴对称实现线段的转移
关键
2
需要注意的细节
区分哪些是定点,哪些是动点,哪条直线是对称轴利用图形的轴对称性,会简化过程.
课后作业
如图, 为 边上的两个定点,在 边上求作一点,使 最短.
最短路径问题
(第一课时)
最值问题
最多
最长
最胖
最少
最短
最瘦
“最短路径问题”
如图,连接 、 两点的所有连线中,哪条最短?为什么
复习1
2
1
3
路线 最短
2
两点之间,线段最短.
点是直线外一点,点 与该直线 上各点连接的所有线段中,哪条最短?为什么?
最短
1
1
1
1
1
1
1
垂线段最短
复习2
如图,在直线上求作一点,使得 最短.
引例
如图,在直线上求作一点,使得 最短.
引例
如图,在直线上求作一点,使得 最短.
引例
如图,在直线上求作一点,使得 最短.
引例
如图,在直线上求作一点,使得 最短.
引例
如图,在直线上求作一点,使得 最短.
引例
如图,在直线上求作一点,使得 最短.
作法
, .
依据
.
引例
如图,牧马人从地出发,到一条笔直的河边 饮马,然后到 地,牧马人到河边的什么地方饮马,可使所走的路径最短?
例
如图,在直线 上求作一点,使 最短.
文字语言
符号语言
图形语言
如图,在直线 上求作一点,使 最短.
例
如图,在直线 上求作一点,使 最短.
例
如图,在直线 上求作一点,使 最短.
例
如图,在直线 上求作一点,使 最短.
例
如图,在直线 上求作一点,使 最短.
例
如图,在直线 上求作一点,使 最短.
例
如图,在直线 上求作一点,使 最短.
例
在直线 同侧
在直线 异侧
引例
能否通过图形的变化(轴对称、平移等),将问题转化为我们研究过的问题呢
思考
如图,在直线 上求作一点,使 最短.
例
如图,在直线 上求作一点,使 最短.
例
问题转化为:
在直线 上求作一点 使 最短.
如图,在直线 上求作一点,使 最短.
例
作法
;
;
.
如图,在直线 上求作一点,使 最短.
例
思考
证明
,
,.
如图,在直线 上求作一点,使 最短.
例
思考
证明
,
,
,.
如图,牧马人从地出发,到一条笔直的河边 饮马,然后到 地,牧马人到河边的什么地方饮马,可使所走的路径最短?
例
如图,在直线 上求作一点,使 最短.
例
总结
1
将实际问题抽象成数学问题,用数学语言表达.
2
利用轴对称转移线段,将问题转化为研究过的引例:即两点之间,线段最短的问题.
3
用符号语言证明结论.
有两棵树位置如图,树的底部分别为 地上有一只昆虫沿着—的路径在地面上爬行. 小树顶处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶 处. 问小鸟飞至之间何处时,飞行距离最短,在图中画出该点的位置.
练习
,.
,.
作法
;
;
.
,.
作法
;
;
.
有两棵树位置如图,树的底部分别为 地上有一只昆虫沿着—的路径在地面上爬行. 小树顶处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶 处. 问小鸟飞至之间何处时,飞行距离最短,在图中画出该点的位置.
练习
作法
;
;
.
如图,已知点,点 分别是等边三角形 中、 边的中点,,点 是 边上的动点,则 的最小值为 .
例
1
1
1
1
1
如图,已知点,点 分别是等边三角形 中、 边的中点,,点 是 边上的动点,则 的最小值为 .
例
1
1
1
1
1
如图,已知点,点 分别是等边三角形 中、 边的中点,,点 是 边上的动点,则 的最小值为 .
例
利用轴对称转移线段,将问题转化为研究过两点之间,线段最短的问题.
方法
问题
和,作哪个点的对称点更好?
如图,已知点,点 分别是等边三角形 中、 边的中点,,点 是 边上的动点,则 的最小值为 .
例
.
思路
.
.
如图,已知点,点 分别是等边三角形 中、 边的中点,,点 是 边上的动点,则 的最小值为 .
例
.
.
.
思路
,
.
如图,已知点,点 分别是等边三角形 中、 边的中点,,点 是 边上的动点,则 的最小值为 .
例
总结
1
分析题目中的定点和动点,转化为我们熟悉的最短路径问题.
2
利用等边三角形的轴对称性找到合适的对称点.
课
堂
小
结
1
最短路径问题
如图,在直线 上求作一点,使得 最短.
在直线 异侧
在直线 同侧
课
堂
小
结
1
最短路径问题
两点之间,线段最短
依据
利用轴对称实现线段的转移
关键
2
需要注意的细节
区分哪些是定点,哪些是动点,哪条直线是对称轴利用图形的轴对称性,会简化过程.
课后作业
如图, 为 边上的两个定点,在 边上求作一点,使 最短.
