全等三角形(3)[上学期]
文档属性
| 名称 | 全等三角形(3)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 304.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-28 08:40:00 | ||
图片预览




文档简介
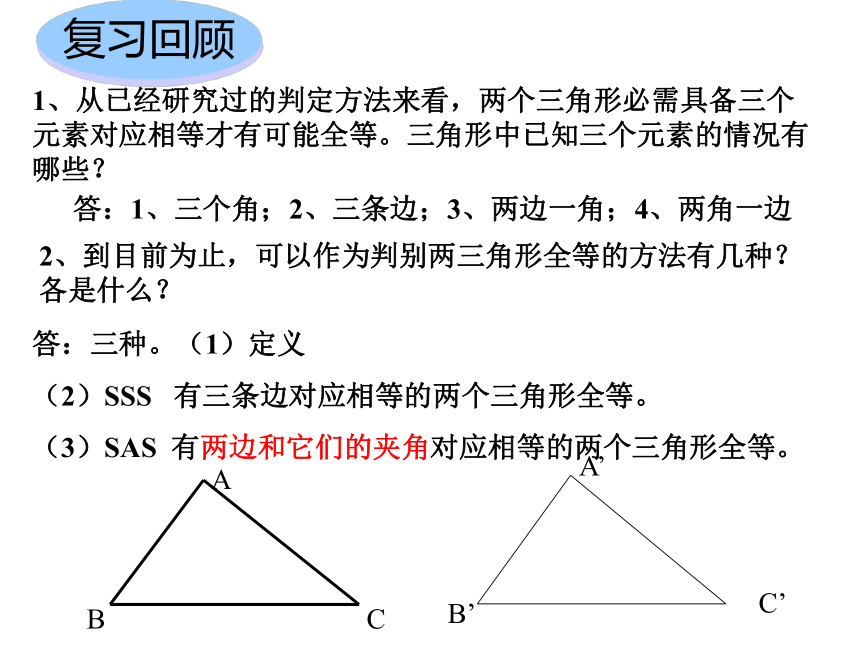
课件19张PPT。全等三角形的条件(三)1、从已经研究过的判定方法来看,两个三角形必需具备三个元素对应相等才有可能全等。三角形中已知三个元素的情况有哪些?答:1、三个角;2、三条边;3、两边一角;4、两角一边2、到目前为止,可以作为判别两三角形全等的方法有几种?各是什么?答:三种。(1)定义
(2)SSS 有三条边对应相等的两个三角形全等。
(3)SAS 有两边和它们的夹角对应相等的两个三角形全等。复习回顾 小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块于原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么?帮帮忙为了解决这个问题,现在让我们以前后桌为一组,共同完成一个实验。实验任意画一个△ABC。
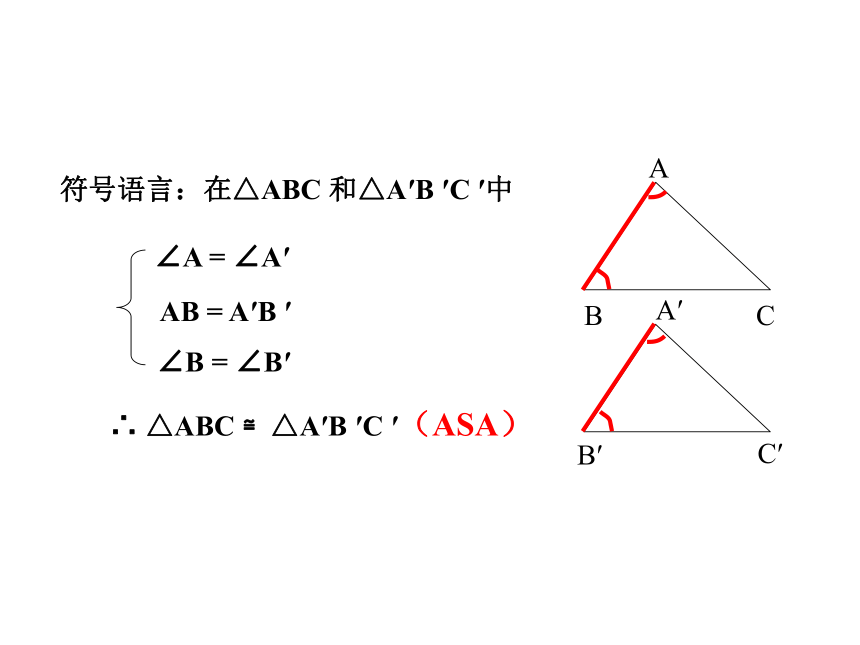
前桌两位同学都各自画△A′B′C′,使A′B′=AB, ∠ A′= ∠ A, ∠ B′= ∠ B; 后桌两位同学各自画△A?B ? C ?,使B ? C ? =BC, ∠ B ? = ∠ B, ∠ C ? = ∠ C(即使两角和它们的夹边对应相等)
把画好的△A′B′C′和△A?B ? C ?剪下,放到△ABC上,你发现了什么?1、按要求画出三角形,并与同伴进行交流。做一做 两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。结论:(1) ∠A=60°、∠B=80°、AB=2cm
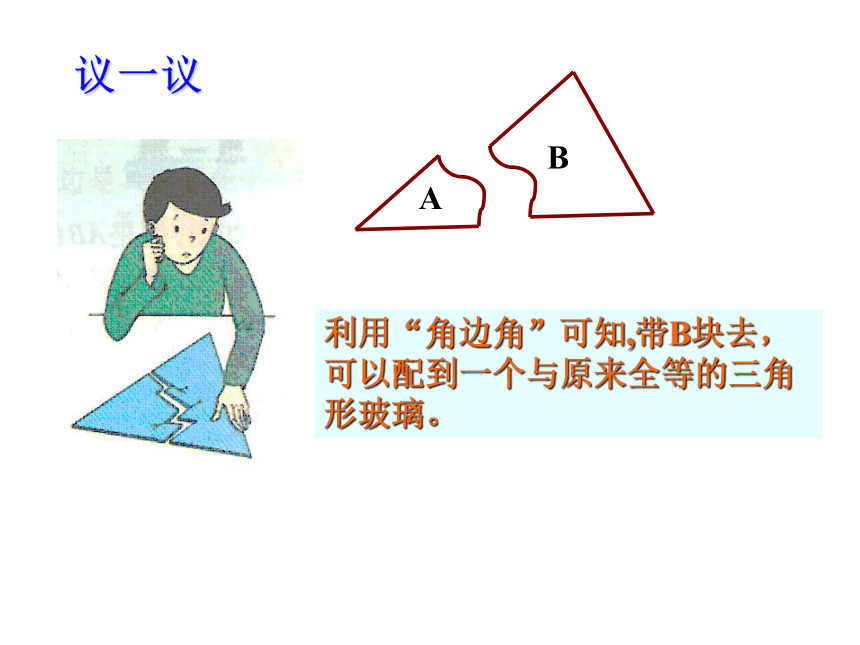
(2)∠A=60°、 ∠B=45°、AB=3cm利用“角边角”可知,带B块去,可以配到一个与原来全等的三角形玻璃。AB议一议探 究 在△ABC 和△DEF 中,CB=EF ,∠A=∠D,∠B=∠E,△ABC 与△DEF全等吗?能利用角边角条件证明你的结论吗?结论: 两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”例1、如图 ,D在AB上,E在AC上AB=AC,∠B=∠C,求证:AD=AE试一试BEDCA证明 :在△ABC和△ADE中
∠A=∠A(公共角)
AC=AE(已知)
∠C=∠E(已知)
∴△ABC≌△ADE(ASA)
∴AB=AD(全等三角形的对应边相等)
又∵AE=AC(已知)
∴BE=DC
O例3 :如图所示, ∠ABC= ∠DCB, ∠ACB= ∠DBC,
求证:AC=DB证明: ∵在△ABC与△DCB中
∠ABC=∠DCB (已知)
∠ACB= ∠DBC (已知)
BC=CB (公共边)
∴ △ABC ≌△DCB (AAS)
∴ AC=DB(全等三角形的对应边相等)探 究 三个角对应相等的两个三角形全等吗?不全等。如: 今天我们经历了对符合两角一边的条件的所有三角形进行画图验证,探索出三角形全等的另两个条件,它们分别是: 两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。 两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”小 结:已知: ∠E= ∠C,EO=CO
求证: △BEO≌ △DCO 练习:如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?思考题12已知: ∠1= ∠2, ∠E= ∠C,
AC=AE
求证:AB=AD ∠B= ∠D证明: ∵ ∠1= ∠2
∴ ∠1+ ∠EAC= ∠2+ ∠EAC
∴ ∠BAC= ∠DAE在△BAC和 △DAE中
∠BAC= ∠DAE
AC=AE
∠C= ∠E
∴△ BAC ≌△ DAE (ASA)
∴AB=AD(全等三角形的对应边相等)
∠B=∠D (全等三角形的对应边相等)BADCE已知: ∠1= ∠2,
∠E= ∠C,AC=AE
D、A、B在一条直线上
求证:点A为线段DB中点证明:∵ ∠1= ∠2
∴ ∠1+ ∠3= ∠2+ ∠3
∴ ∠ DAE = ∠ BAC
在△DAE和△BAC中
∠ DAE = ∠ BAC
AE=AC
∠E= ∠C
∴ △DAE△BAC(ASA)
∴AD=AB
∴点A为线段DB中点例4123再见!
(2)SSS 有三条边对应相等的两个三角形全等。
(3)SAS 有两边和它们的夹角对应相等的两个三角形全等。复习回顾 小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块于原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么?帮帮忙为了解决这个问题,现在让我们以前后桌为一组,共同完成一个实验。实验任意画一个△ABC。
前桌两位同学都各自画△A′B′C′,使A′B′=AB, ∠ A′= ∠ A, ∠ B′= ∠ B; 后桌两位同学各自画△A?B ? C ?,使B ? C ? =BC, ∠ B ? = ∠ B, ∠ C ? = ∠ C(即使两角和它们的夹边对应相等)
把画好的△A′B′C′和△A?B ? C ?剪下,放到△ABC上,你发现了什么?1、按要求画出三角形,并与同伴进行交流。做一做 两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。结论:(1) ∠A=60°、∠B=80°、AB=2cm
(2)∠A=60°、 ∠B=45°、AB=3cm利用“角边角”可知,带B块去,可以配到一个与原来全等的三角形玻璃。AB议一议探 究 在△ABC 和△DEF 中,CB=EF ,∠A=∠D,∠B=∠E,△ABC 与△DEF全等吗?能利用角边角条件证明你的结论吗?结论: 两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”例1、如图 ,D在AB上,E在AC上AB=AC,∠B=∠C,求证:AD=AE试一试BEDCA证明 :在△ABC和△ADE中
∠A=∠A(公共角)
AC=AE(已知)
∠C=∠E(已知)
∴△ABC≌△ADE(ASA)
∴AB=AD(全等三角形的对应边相等)
又∵AE=AC(已知)
∴BE=DC
O例3 :如图所示, ∠ABC= ∠DCB, ∠ACB= ∠DBC,
求证:AC=DB证明: ∵在△ABC与△DCB中
∠ABC=∠DCB (已知)
∠ACB= ∠DBC (已知)
BC=CB (公共边)
∴ △ABC ≌△DCB (AAS)
∴ AC=DB(全等三角形的对应边相等)探 究 三个角对应相等的两个三角形全等吗?不全等。如: 今天我们经历了对符合两角一边的条件的所有三角形进行画图验证,探索出三角形全等的另两个条件,它们分别是: 两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。 两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”小 结:已知: ∠E= ∠C,EO=CO
求证: △BEO≌ △DCO 练习:如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?思考题12已知: ∠1= ∠2, ∠E= ∠C,
AC=AE
求证:AB=AD ∠B= ∠D证明: ∵ ∠1= ∠2
∴ ∠1+ ∠EAC= ∠2+ ∠EAC
∴ ∠BAC= ∠DAE在△BAC和 △DAE中
∠BAC= ∠DAE
AC=AE
∠C= ∠E
∴△ BAC ≌△ DAE (ASA)
∴AB=AD(全等三角形的对应边相等)
∠B=∠D (全等三角形的对应边相等)BADCE已知: ∠1= ∠2,
∠E= ∠C,AC=AE
D、A、B在一条直线上
求证:点A为线段DB中点证明:∵ ∠1= ∠2
∴ ∠1+ ∠3= ∠2+ ∠3
∴ ∠ DAE = ∠ BAC
在△DAE和△BAC中
∠ DAE = ∠ BAC
AE=AC
∠E= ∠C
∴ △DAE△BAC(ASA)
∴AD=AB
∴点A为线段DB中点例4123再见!
