人教版九年级数学上册《点和圆的位置关系》第2课时 课件(共25张PPT)
文档属性
| 名称 | 人教版九年级数学上册《点和圆的位置关系》第2课时 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 22:03:58 | ||
图片预览


文档简介
(共25张PPT)
(第二课时)
点和圆的位置关系
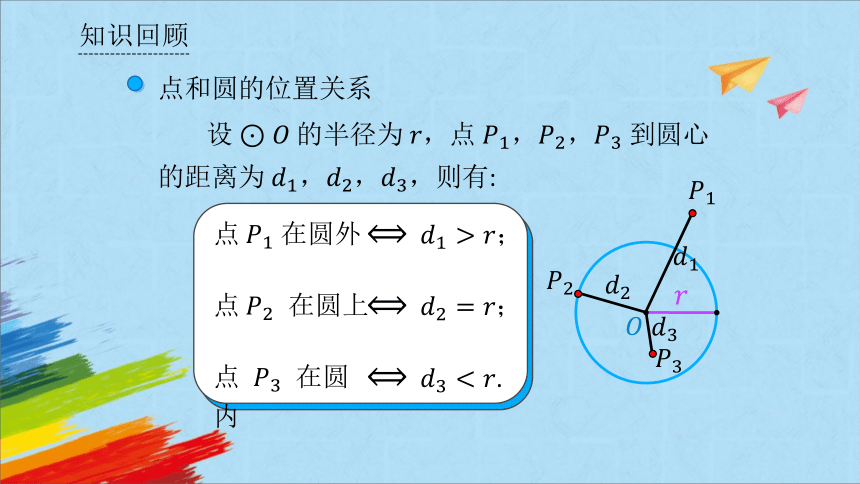
知识回顾
半径为 ,点, 到圆心的距离为,,则有:
点在圆外
;
点 在圆上
;
点 在圆内
.
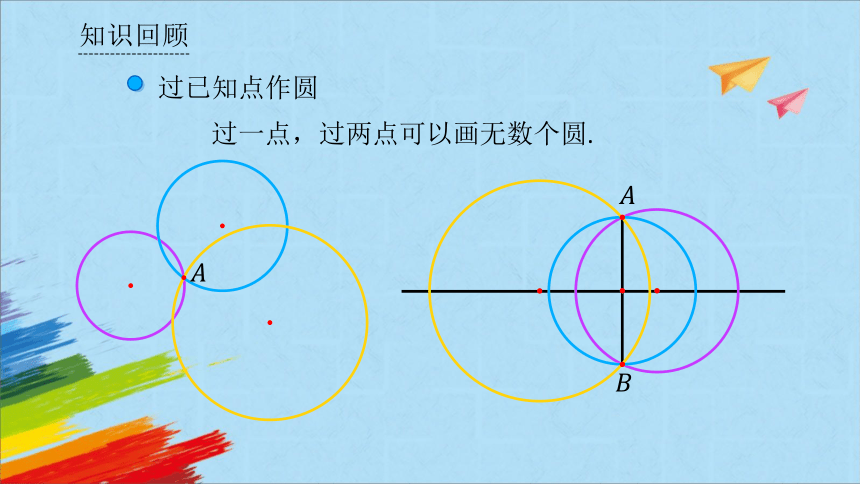
知识回顾
.
探究“过已知点作圆”
经过三个已知点 作圆.
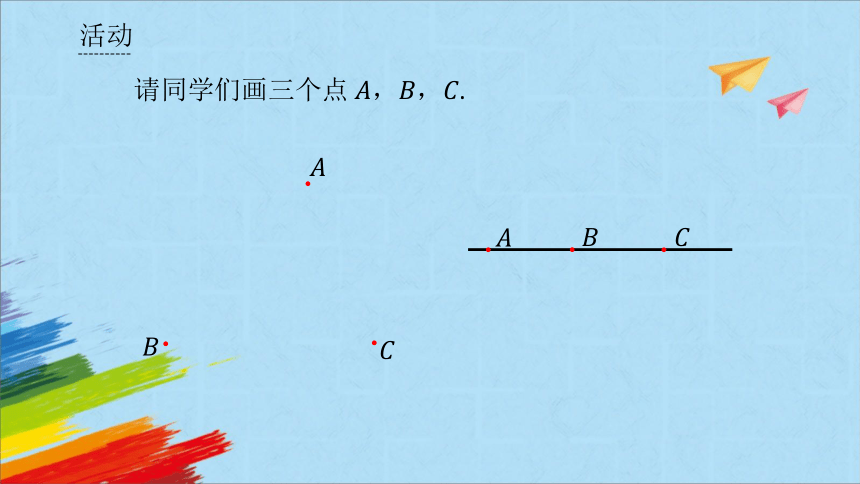
活动
请同学们画三个点.
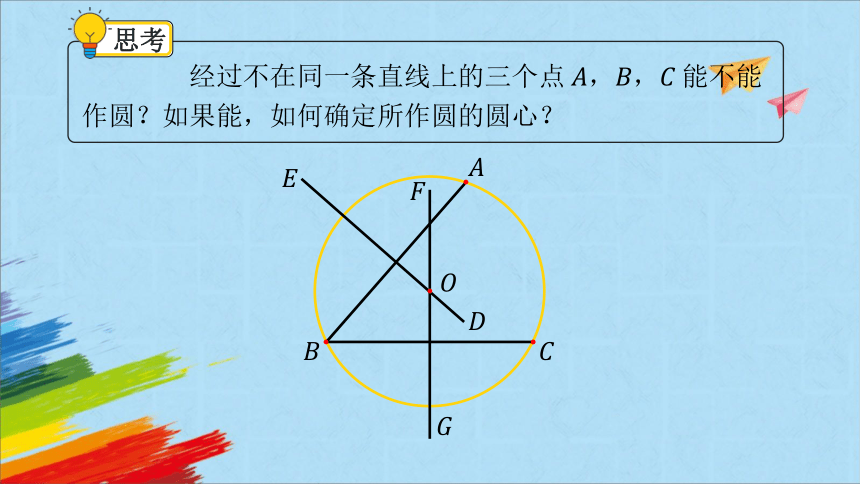
经过不在同一条直线上的三个点能不能作圆?如果能,如何确定所作圆的圆心?
思考
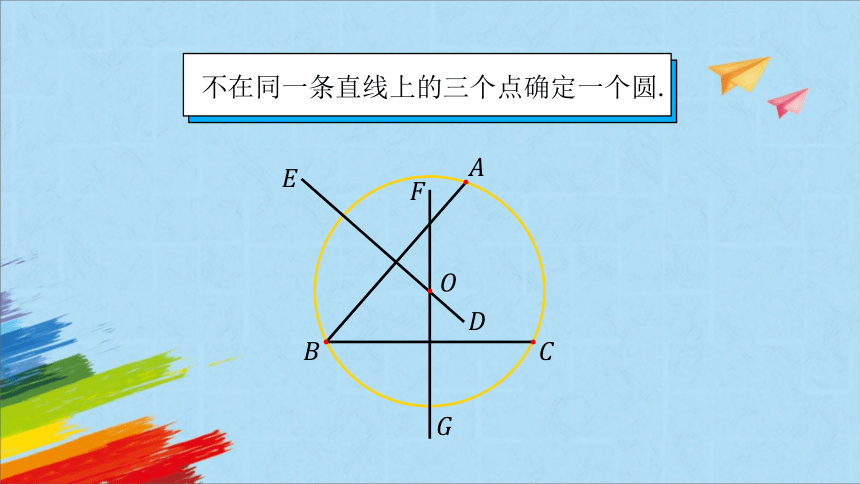
不在同一条直线上的三个点确定一个圆.
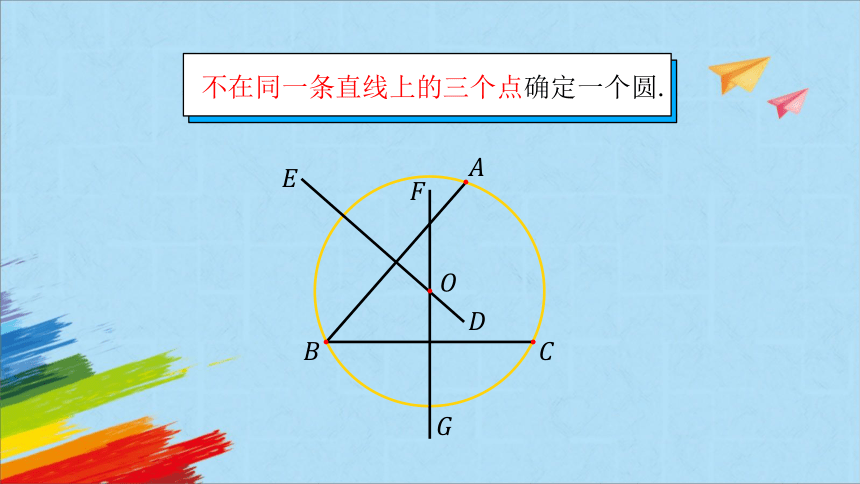
不在同一条直线上的三个点确定一个圆.
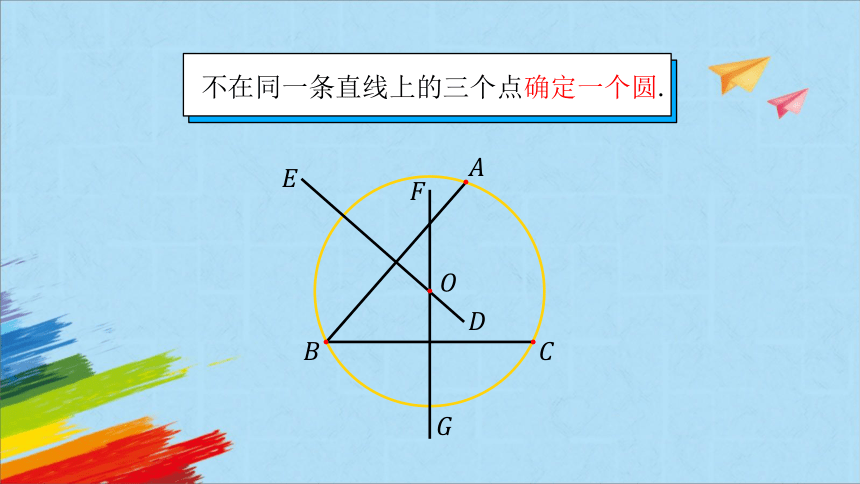
不在同一条直线上的三个点确定一个圆.
三角形的外接圆;圆的内接三角形;外心.
概念
外心是三角形三边的垂直平分线的交点;
外心到三角形顶点的距离相等.
请作出锐角三角形、直角三角形、钝角三角形的外接圆.这些外接圆的圆心在什么位置?
试一试
三角形内
斜边中点
三角形外
巩固练习
如图, 所在的直线垂直平分线段,怎么用这样的工具找到圆形工件的圆心?
1
巩固练习
小腾家的圆形镜子损坏了,他要定制一个大小相同的新镜子,如何测量镜子的半径?
2
巩固练习
已知,△ 中,若,,求△ 的外接圆半径.
3
解:
直角三角形的外心在斜边的中点,斜边就是直径,
根据勾股定理得,
所以△ 的外接圆半径为.
经过同一条直线上的三个点能作出一个圆吗?如何证明你的结论?
思考
证明
经过同一条直线上的三点不能作圆.
假设命题的结论不成立,经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立,这种方法叫做反证法.
巩固练习
判断下列说法是否正确
4
任意的一个三角形一定有一个外接圆
三角形的外心到三角形各顶点的距离相等
巩固练习
若一个三角形的外心在一边上,则此三角形的形状为( )
5
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
课
堂
小
结
半径为 ,点, 到圆心的距离为,,则有:
点在圆外
;
点 在圆上
;
点 在圆内
.
课
堂
小
结
.
.
假设命题的结论不成立,经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立,这种方法叫做反证法.
课后作业
如图,分别作出锐角三角形、直角三角形和钝角三角形的外接圆,它们外心的位置有什么特点?
1
课后作业
如图是一名考古学家发现的一块古代车轮的碎片,你能帮他找出这个轮子的半径吗?说出你的理由.
2
请用反证法证明“两直线平行,同位角相等”.
试一试
已知:
求证:.
假设不正确
经过任意四个点是不是可以作一个圆?
思考
四个点都在同一条直线上;
四个点中,有三个点在同一条直线上,而另一个点不在这条直线上;
四个点中的任意三点,都不在同一直线上.
(第二课时)
点和圆的位置关系
知识回顾
半径为 ,点, 到圆心的距离为,,则有:
点在圆外
;
点 在圆上
;
点 在圆内
.
知识回顾
.
探究“过已知点作圆”
经过三个已知点 作圆.
活动
请同学们画三个点.
经过不在同一条直线上的三个点能不能作圆?如果能,如何确定所作圆的圆心?
思考
不在同一条直线上的三个点确定一个圆.
不在同一条直线上的三个点确定一个圆.
不在同一条直线上的三个点确定一个圆.
三角形的外接圆;圆的内接三角形;外心.
概念
外心是三角形三边的垂直平分线的交点;
外心到三角形顶点的距离相等.
请作出锐角三角形、直角三角形、钝角三角形的外接圆.这些外接圆的圆心在什么位置?
试一试
三角形内
斜边中点
三角形外
巩固练习
如图, 所在的直线垂直平分线段,怎么用这样的工具找到圆形工件的圆心?
1
巩固练习
小腾家的圆形镜子损坏了,他要定制一个大小相同的新镜子,如何测量镜子的半径?
2
巩固练习
已知,△ 中,若,,求△ 的外接圆半径.
3
解:
直角三角形的外心在斜边的中点,斜边就是直径,
根据勾股定理得,
所以△ 的外接圆半径为.
经过同一条直线上的三个点能作出一个圆吗?如何证明你的结论?
思考
证明
经过同一条直线上的三点不能作圆.
假设命题的结论不成立,经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立,这种方法叫做反证法.
巩固练习
判断下列说法是否正确
4
任意的一个三角形一定有一个外接圆
三角形的外心到三角形各顶点的距离相等
巩固练习
若一个三角形的外心在一边上,则此三角形的形状为( )
5
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
课
堂
小
结
半径为 ,点, 到圆心的距离为,,则有:
点在圆外
;
点 在圆上
;
点 在圆内
.
课
堂
小
结
.
.
假设命题的结论不成立,经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立,这种方法叫做反证法.
课后作业
如图,分别作出锐角三角形、直角三角形和钝角三角形的外接圆,它们外心的位置有什么特点?
1
课后作业
如图是一名考古学家发现的一块古代车轮的碎片,你能帮他找出这个轮子的半径吗?说出你的理由.
2
请用反证法证明“两直线平行,同位角相等”.
试一试
已知:
求证:.
假设不正确
经过任意四个点是不是可以作一个圆?
思考
四个点都在同一条直线上;
四个点中,有三个点在同一条直线上,而另一个点不在这条直线上;
四个点中的任意三点,都不在同一直线上.
同课章节目录
