人教版九年级数学上册《点和圆的位置关系》第1课时 课件(共28张PPT)
文档属性
| 名称 | 人教版九年级数学上册《点和圆的位置关系》第1课时 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 22:05:09 | ||
图片预览




文档简介
(共28张PPT)
(第一课时)
点和圆的位置关系
下图是一位射击运动员,六发子弹在射击靶上留下的痕迹.
射击靶由许多同心圆构成的,这些圆的圆心相同,半径不同.你知道击中靶的不同位置的成绩是如何计算的吗?
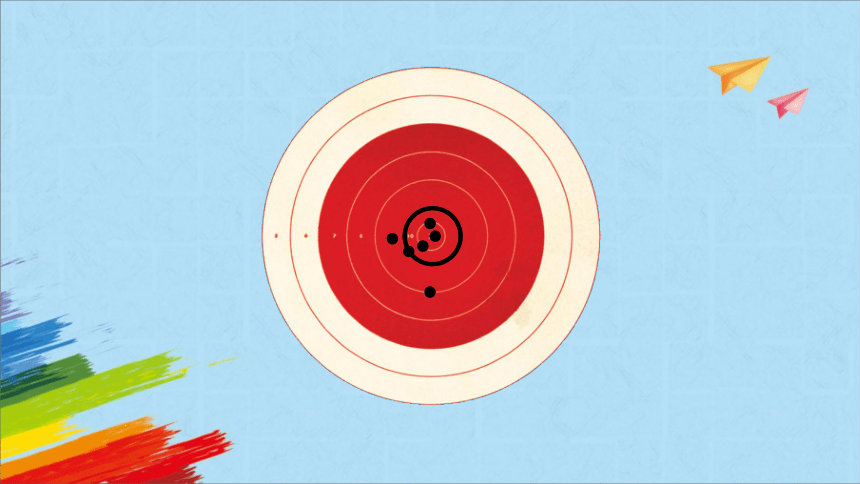
请同学们观察点和圆的位置关系,对这六个点进行分类.
点在圆外
点在圆上
点在圆内
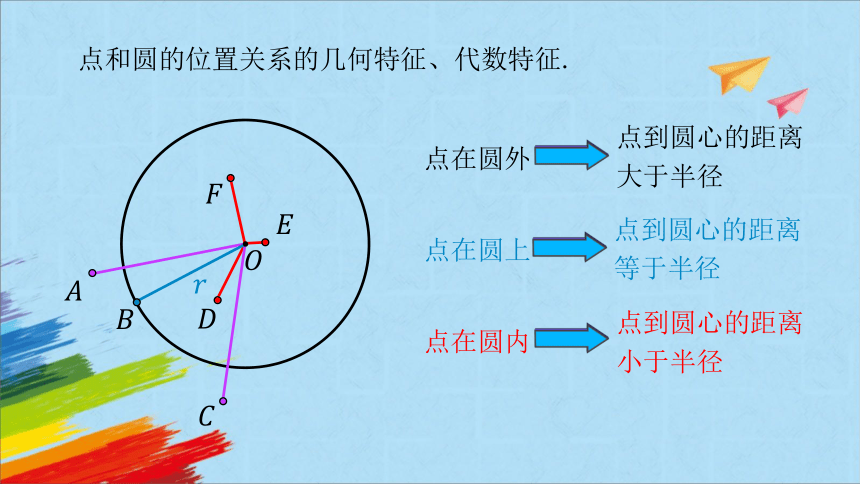
点和圆的位置关系的几何特征、代数特征.
点在圆外
点在圆上
点在圆内
点到圆心的距离大于半径
点到圆心的距离等于半径
点到圆心的距离小于半径
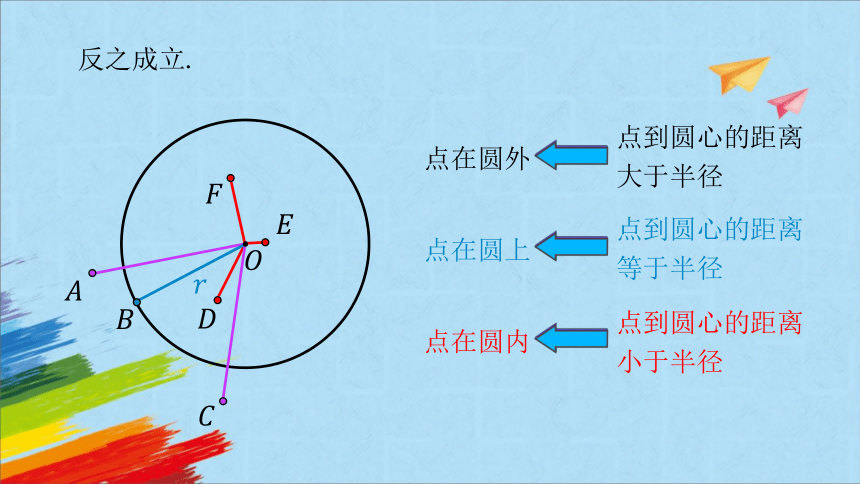
反之成立.
点在圆外
点在圆上
点在圆内
点到圆心的距离大于半径
点到圆心的距离等于半径
点到圆心的距离小于半径
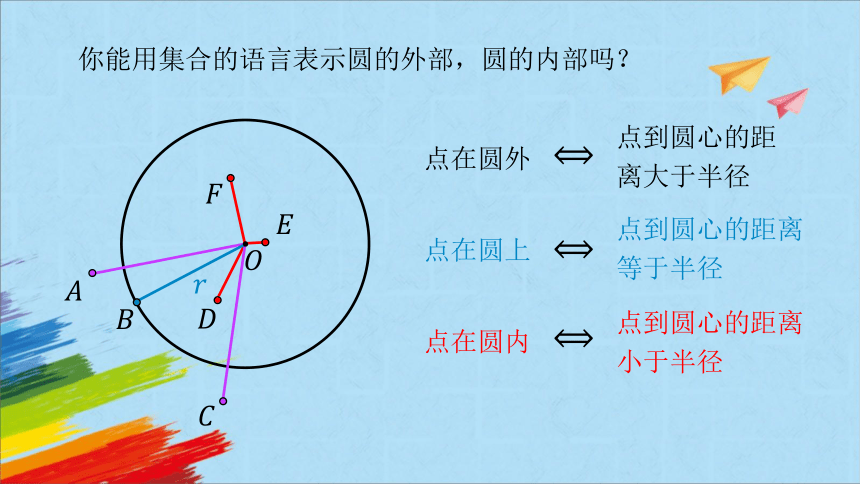
你能用集合的语言表示圆的外部,圆的内部吗?
点在圆外
点在圆上
点在圆内
点到圆心的距离大于半径
点到圆心的距离等于半径
点到圆心的距离小于半径
基本概念
点在圆外
;
点在圆上
;
点在圆内
.
巩固练习
画出由所有到已知点 的距离大于或等于并且小于或等于的点组成的图形.
1
巩固练习
画出由所有到已知点 的距离大于或等于并且小于或等于的点组成的图形.
1
巩固练习
画出由所有到已知点 的距离大于或等于并且小于或等于的点组成的图形.
1
弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击成绩越好.
巩固练习
体育课上,小明和小丽的铅球成绩分别是和,他们投出的铅球分别落在图中哪个区域内
2
小明
小丽
巩固练习
的面积为 :
3
若,则点 在 ;
若,则点 在 ;
若 ,则点 在圆上;
若点 不在圆外,则 .
圆外
圆内
类比探究
两点确定一条直线.
几点确定一个圆
探究“过已知点作圆”
我们知道,已知圆心和半径,可以作一个圆. 经过一个已知点 能不能作圆,这样的圆你能作出多少个?经过两个已知点, 能不能作圆?如果能,圆心分布有什么特点?
思考
探究“过已知点作圆”
经过一个已知点作圆.
结论
过一点可以画无数个圆.
圆心为这个点以外任意一点.
探究“过已知点作圆”
经过两个已知点 作圆.
结论
过两点可以画无数个圆.
圆心在两点所连线段的垂直平分线上.
经过三个已知点 作圆.
思考
巩固练习
.
4
以点 为圆心, 为半径作圆,则点 与圆 的位置关系如何?
以点 为圆心, 为半径作圆,则点 与圆 的位置关系如何?
以点 为圆心, 为半径作圆,则点 与圆 的位置关系如何?
巩固练习
.
4
以点 为圆心, 为半径作圆,则点 与圆 的位置关系如何?
巩固练习
.
4
以点 为圆心, 为半径作圆,则点 与圆 的位置关系如何?
巩固练习
.
4
以点 为圆心, 为半径作圆,则点 与圆 的位置关系如何?
课
堂
小
结
半径为 ,点, 到圆心的距离为,,则有:
点在圆外
;
点 在圆上
;
点 在圆内
.
课
堂
小
结
.
课后作业
的半径为,根据下列点 到圆心 的距离,判断点 和 的位置关系:
1
.
的半径为,当 时,点 在 ;当 时,点 在圆内;当 时,点 不在圆外.
2
课后作业
已知,画半径为 的圆,使它经过两点. 这样的圆能画出多少个?如果半径为呢?
3
思考:经过三个已知点 作圆.
4
(第一课时)
点和圆的位置关系
下图是一位射击运动员,六发子弹在射击靶上留下的痕迹.
射击靶由许多同心圆构成的,这些圆的圆心相同,半径不同.你知道击中靶的不同位置的成绩是如何计算的吗?
请同学们观察点和圆的位置关系,对这六个点进行分类.
点在圆外
点在圆上
点在圆内
点和圆的位置关系的几何特征、代数特征.
点在圆外
点在圆上
点在圆内
点到圆心的距离大于半径
点到圆心的距离等于半径
点到圆心的距离小于半径
反之成立.
点在圆外
点在圆上
点在圆内
点到圆心的距离大于半径
点到圆心的距离等于半径
点到圆心的距离小于半径
你能用集合的语言表示圆的外部,圆的内部吗?
点在圆外
点在圆上
点在圆内
点到圆心的距离大于半径
点到圆心的距离等于半径
点到圆心的距离小于半径
基本概念
点在圆外
;
点在圆上
;
点在圆内
.
巩固练习
画出由所有到已知点 的距离大于或等于并且小于或等于的点组成的图形.
1
巩固练习
画出由所有到已知点 的距离大于或等于并且小于或等于的点组成的图形.
1
巩固练习
画出由所有到已知点 的距离大于或等于并且小于或等于的点组成的图形.
1
弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击成绩越好.
巩固练习
体育课上,小明和小丽的铅球成绩分别是和,他们投出的铅球分别落在图中哪个区域内
2
小明
小丽
巩固练习
的面积为 :
3
若,则点 在 ;
若,则点 在 ;
若 ,则点 在圆上;
若点 不在圆外,则 .
圆外
圆内
类比探究
两点确定一条直线.
几点确定一个圆
探究“过已知点作圆”
我们知道,已知圆心和半径,可以作一个圆. 经过一个已知点 能不能作圆,这样的圆你能作出多少个?经过两个已知点, 能不能作圆?如果能,圆心分布有什么特点?
思考
探究“过已知点作圆”
经过一个已知点作圆.
结论
过一点可以画无数个圆.
圆心为这个点以外任意一点.
探究“过已知点作圆”
经过两个已知点 作圆.
结论
过两点可以画无数个圆.
圆心在两点所连线段的垂直平分线上.
经过三个已知点 作圆.
思考
巩固练习
.
4
以点 为圆心, 为半径作圆,则点 与圆 的位置关系如何?
以点 为圆心, 为半径作圆,则点 与圆 的位置关系如何?
以点 为圆心, 为半径作圆,则点 与圆 的位置关系如何?
巩固练习
.
4
以点 为圆心, 为半径作圆,则点 与圆 的位置关系如何?
巩固练习
.
4
以点 为圆心, 为半径作圆,则点 与圆 的位置关系如何?
巩固练习
.
4
以点 为圆心, 为半径作圆,则点 与圆 的位置关系如何?
课
堂
小
结
半径为 ,点, 到圆心的距离为,,则有:
点在圆外
;
点 在圆上
;
点 在圆内
.
课
堂
小
结
.
课后作业
的半径为,根据下列点 到圆心 的距离,判断点 和 的位置关系:
1
.
的半径为,当 时,点 在 ;当 时,点 在圆内;当 时,点 不在圆外.
2
课后作业
已知,画半径为 的圆,使它经过两点. 这样的圆能画出多少个?如果半径为呢?
3
思考:经过三个已知点 作圆.
4
同课章节目录
