人教版九年级数学上册《二次函数y=a(x-h)?+k的图象和性质》第1课时 课件(共22张PPT)
文档属性
| 名称 | 人教版九年级数学上册《二次函数y=a(x-h)?+k的图象和性质》第1课时 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 00:00:00 | ||
图片预览


文档简介
(共22张PPT)
二次函数
的图象和性质
(第一课时)
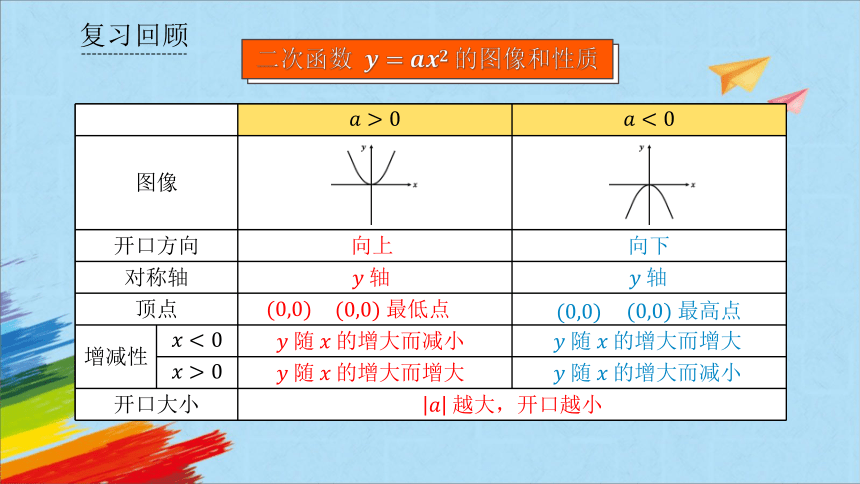
二次函数 的图像和性质
复习回顾
图像
开口方向
对称轴
顶点
增减性
开口大小
图像
开口方向
对称轴
顶点
增减性
开口大小 向上
向下
轴
轴
最低点
最高点
随 的增大而减小
随 的增大而增大
随 的增大而增大
随 的增大而减小
越大,开口越小
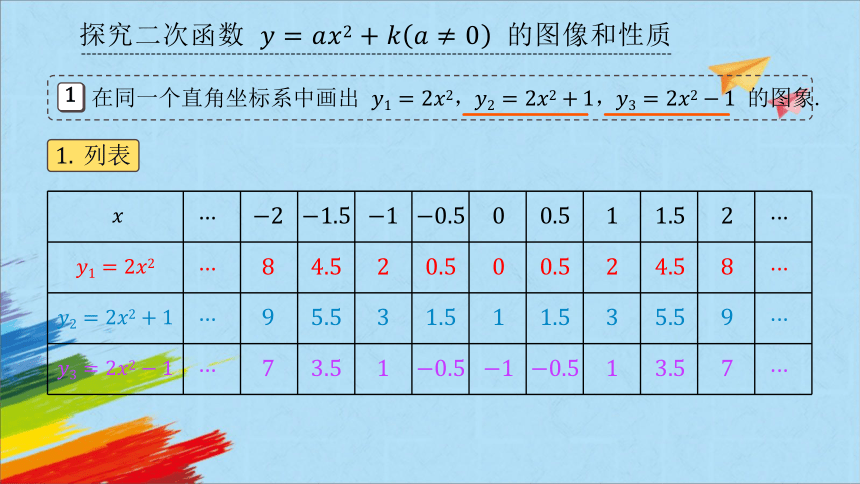
探究二次函数 的图像和性质
1
在同一个直角坐标系中画出 ,, 的图象.
列表
···
···
···
···
···
···
···
···
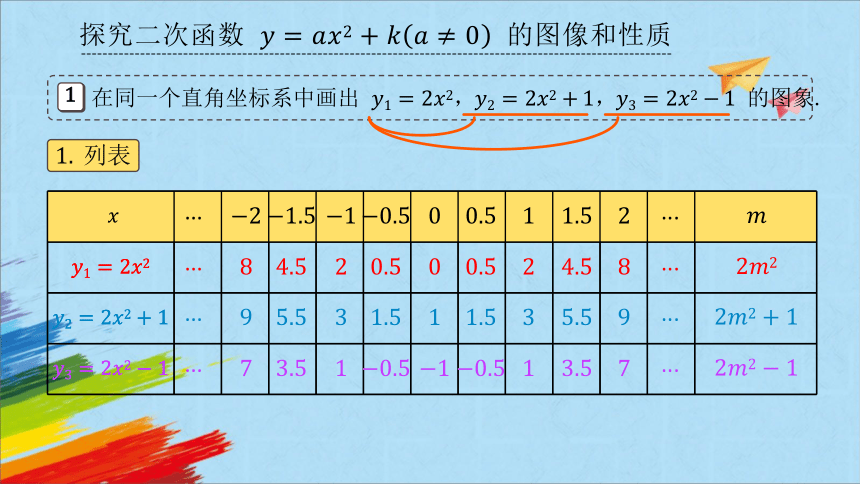
探究二次函数 的图像和性质
1
在同一个直角坐标系中画出 ,, 的图象.
列表
···
···
···
···
···
···
···
···
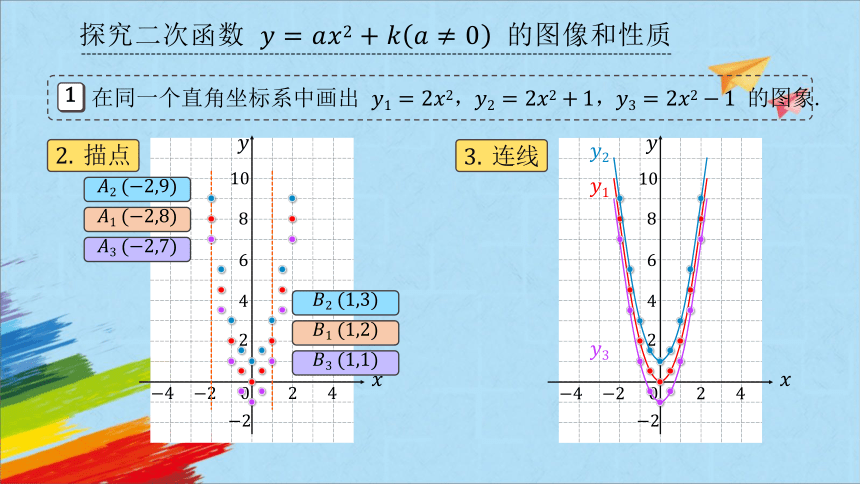
探究二次函数 的图像和性质
描点
1
在同一个直角坐标系中画出 ,, 的图象.
探究二次函数 的图像和性质
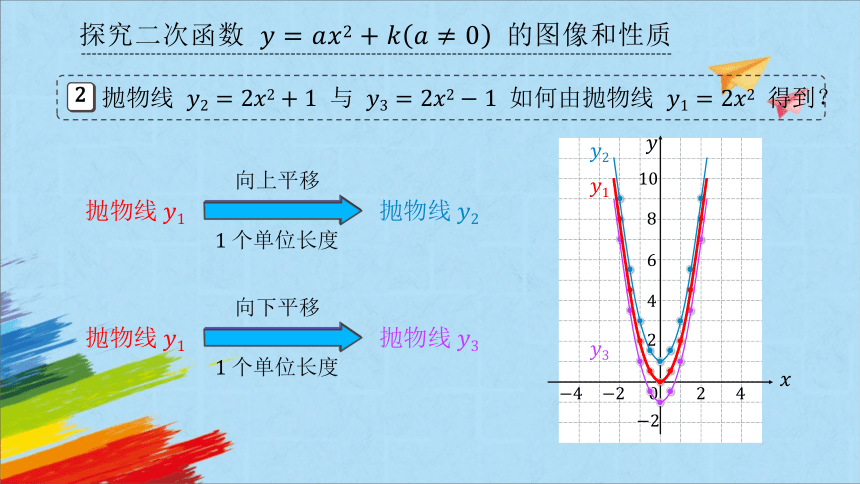
2
抛物线 与 如何由抛物线 得到?
抛物线
抛物线
向上平移
个单位长度
抛物线
抛物线
向下平移
个单位长度
探究二次函数 的图像和性质
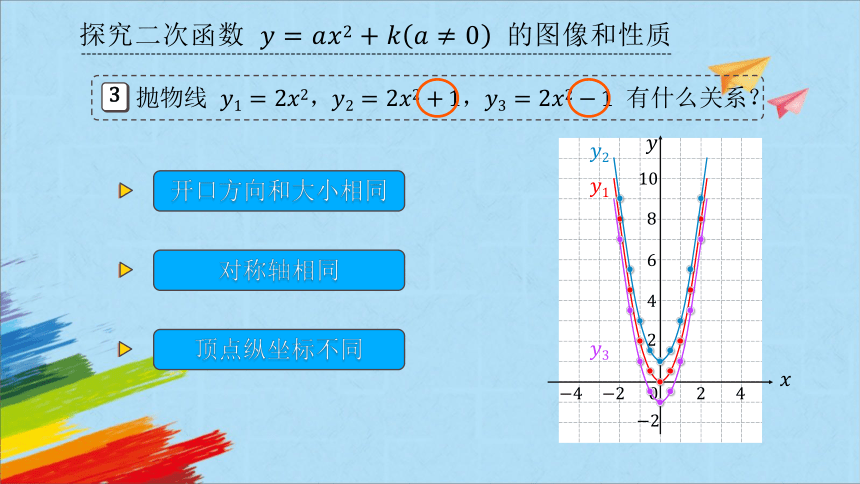
3
抛物线 ,, 有什么关系?
开口方向和大小相同
对称轴相同
顶点纵坐标不同
探究二次函数 的图像和性质
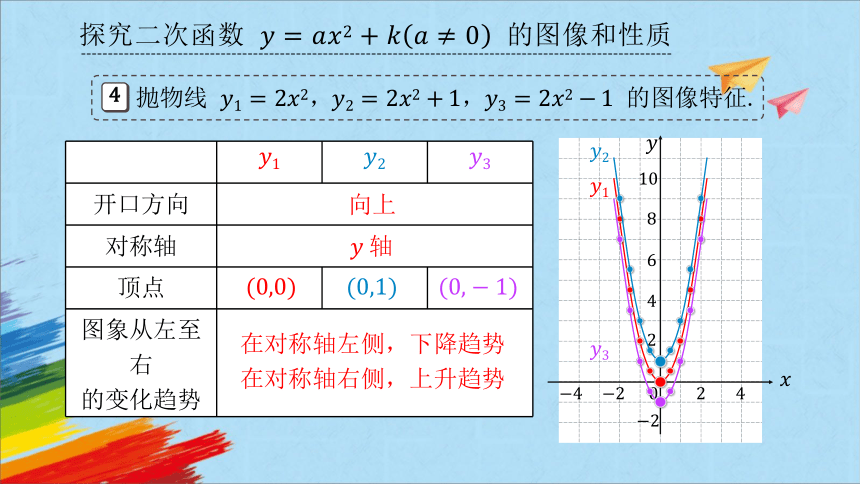
4
抛物线 ,, 的图像特征.
开口方向 对称轴 顶点
图象从左至右 的变化趋势 向上
轴
在对称轴左侧,下降趋势
在对称轴右侧,上升趋势
例题分析
在同一直角坐标系中画出 , 和 的图象,并说明 , 如何由 的图象得到.
题中二次函数均满足 的形式,但此时 ,它又会引起图像的哪些变化呢?是开口,对称轴,顶点,还是
图像的变化趋势呢?
思考
例题分析
在同一直角坐标系中画出 , 和 的图象,并说明 , 如何由 的图象得到.
···
···
···
···
···
···
···
···
···
···
···
···
···
···
···
···
例题分析
在同一直角坐标系中画出 , 和 的图象,并说明 , 如何由 的图象得到.
例题分析
在同一直角坐标系中画出 , 和 的图象,并说明 , 如何由 的图象得到.
的图象向上平移 个单位长度
得到 的图象;
的图象向下平移 个单位长度
得到 的图象.
图像
开口方向
对称轴
顶点
图象从左至右 的变化趋势 在对称轴左侧
在对称轴右侧
图像
开口方向
对称轴
顶点
图象从左至右 的变化趋势 在对称轴左侧
在对称轴右侧
探究二次函数 的图像和性质
5
抛物线 的图像特征.
向上
向下
轴
轴
最低点
最高点
下降趋势
上升趋势
上升趋势
下降趋势
探究二次函数 的图像和性质
6
抛物线 的性质.
图像特征
函数性质
顶点
最值
最低点
最高点
有最小值是
有最大值是
探究二次函数 的图像和性质
6
抛物线 的性质.
图像从左至右的变化趋势
在对称轴左侧
在对称轴右侧
下降
上升
上升
增减性
随 的增大而减小
随 的增大而增大
随 的增大而增大
随 的增大而减小
探究二次函数 的图像和性质
7
抛物线 可以如何由抛物线 得到?
当
向上平移 个单位长度
顶点
顶点
当
向下平移 || 个单位长度
分析
相同,则两条抛物线的形状是相同,可以通过平移得到.
巩固练习
抛物线 的开口 ,对称轴是 ,
图象存在最 点,坐标是 ,当 时, 随 的增大而增大,当 时, 随 的增大而减小.
向下
轴
高
1
巩固练习
把抛物线 向下平移 个单位长度,可以得到抛物线
,再向上平移 个单位长度,可以得到抛物线
.
2
向下平移
两个单位长度
顶点
向上平移
个单位长度
分析
顶点的平移可以代替抛物线的平移.
图像
开口方向
对称轴
顶点
图象从左至右 的变化趋势 在对称轴左侧
在对称轴右侧
图像
开口方向
对称轴
顶点
图象从左至右 的变化趋势 在对称轴左侧
在对称轴右侧
图像
开口方向
对称轴
顶点
图象从左至右 的变化趋势 在对称轴左侧
在对称轴右侧
课
堂
小
结
通过本节课的学习,学到了关于 的哪些知识呢?
向上
向下
轴
轴
最低点
最高点
下降趋势
上升趋势
上升趋势
下降趋势
最值
增减性
最值
增减性
最值
增减性
课
堂
小
结
随 的增大而减小
随 的增大而增大
随 的增大而增大
随 的增大而减小
有最小值
有最大值
通过本节课的学习,学到了关于 的哪些知识呢?
课
堂
小
结
通过本节课的学习,学到了关于 的哪些知识呢?
当
向上平移 个单位长度
当
向下平移 || 个单位长度
抛物线 的顶点坐标是 ,对称轴 ,
当 时, 有最 值是 ;它可以由抛物线
向 平移 个单位长度得到.
已知抛物线 经过点 .
将上述抛物线向下平移 个单位长度,求所得抛物线的解析式;
若点 为抛物线 上一点,直线 轴于 ,,
沿 轴平移抛物线 ,使之经过点 ,求平移后所得抛物
线的解析式.
1
2
课后作业
二次函数
的图象和性质
(第一课时)
二次函数 的图像和性质
复习回顾
图像
开口方向
对称轴
顶点
增减性
开口大小
图像
开口方向
对称轴
顶点
增减性
开口大小 向上
向下
轴
轴
最低点
最高点
随 的增大而减小
随 的增大而增大
随 的增大而增大
随 的增大而减小
越大,开口越小
探究二次函数 的图像和性质
1
在同一个直角坐标系中画出 ,, 的图象.
列表
···
···
···
···
···
···
···
···
探究二次函数 的图像和性质
1
在同一个直角坐标系中画出 ,, 的图象.
列表
···
···
···
···
···
···
···
···
探究二次函数 的图像和性质
描点
1
在同一个直角坐标系中画出 ,, 的图象.
探究二次函数 的图像和性质
2
抛物线 与 如何由抛物线 得到?
抛物线
抛物线
向上平移
个单位长度
抛物线
抛物线
向下平移
个单位长度
探究二次函数 的图像和性质
3
抛物线 ,, 有什么关系?
开口方向和大小相同
对称轴相同
顶点纵坐标不同
探究二次函数 的图像和性质
4
抛物线 ,, 的图像特征.
开口方向 对称轴 顶点
图象从左至右 的变化趋势 向上
轴
在对称轴左侧,下降趋势
在对称轴右侧,上升趋势
例题分析
在同一直角坐标系中画出 , 和 的图象,并说明 , 如何由 的图象得到.
题中二次函数均满足 的形式,但此时 ,它又会引起图像的哪些变化呢?是开口,对称轴,顶点,还是
图像的变化趋势呢?
思考
例题分析
在同一直角坐标系中画出 , 和 的图象,并说明 , 如何由 的图象得到.
···
···
···
···
···
···
···
···
···
···
···
···
···
···
···
···
例题分析
在同一直角坐标系中画出 , 和 的图象,并说明 , 如何由 的图象得到.
例题分析
在同一直角坐标系中画出 , 和 的图象,并说明 , 如何由 的图象得到.
的图象向上平移 个单位长度
得到 的图象;
的图象向下平移 个单位长度
得到 的图象.
图像
开口方向
对称轴
顶点
图象从左至右 的变化趋势 在对称轴左侧
在对称轴右侧
图像
开口方向
对称轴
顶点
图象从左至右 的变化趋势 在对称轴左侧
在对称轴右侧
探究二次函数 的图像和性质
5
抛物线 的图像特征.
向上
向下
轴
轴
最低点
最高点
下降趋势
上升趋势
上升趋势
下降趋势
探究二次函数 的图像和性质
6
抛物线 的性质.
图像特征
函数性质
顶点
最值
最低点
最高点
有最小值是
有最大值是
探究二次函数 的图像和性质
6
抛物线 的性质.
图像从左至右的变化趋势
在对称轴左侧
在对称轴右侧
下降
上升
上升
增减性
随 的增大而减小
随 的增大而增大
随 的增大而增大
随 的增大而减小
探究二次函数 的图像和性质
7
抛物线 可以如何由抛物线 得到?
当
向上平移 个单位长度
顶点
顶点
当
向下平移 || 个单位长度
分析
相同,则两条抛物线的形状是相同,可以通过平移得到.
巩固练习
抛物线 的开口 ,对称轴是 ,
图象存在最 点,坐标是 ,当 时, 随 的增大而增大,当 时, 随 的增大而减小.
向下
轴
高
1
巩固练习
把抛物线 向下平移 个单位长度,可以得到抛物线
,再向上平移 个单位长度,可以得到抛物线
.
2
向下平移
两个单位长度
顶点
向上平移
个单位长度
分析
顶点的平移可以代替抛物线的平移.
图像
开口方向
对称轴
顶点
图象从左至右 的变化趋势 在对称轴左侧
在对称轴右侧
图像
开口方向
对称轴
顶点
图象从左至右 的变化趋势 在对称轴左侧
在对称轴右侧
图像
开口方向
对称轴
顶点
图象从左至右 的变化趋势 在对称轴左侧
在对称轴右侧
课
堂
小
结
通过本节课的学习,学到了关于 的哪些知识呢?
向上
向下
轴
轴
最低点
最高点
下降趋势
上升趋势
上升趋势
下降趋势
最值
增减性
最值
增减性
最值
增减性
课
堂
小
结
随 的增大而减小
随 的增大而增大
随 的增大而增大
随 的增大而减小
有最小值
有最大值
通过本节课的学习,学到了关于 的哪些知识呢?
课
堂
小
结
通过本节课的学习,学到了关于 的哪些知识呢?
当
向上平移 个单位长度
当
向下平移 || 个单位长度
抛物线 的顶点坐标是 ,对称轴 ,
当 时, 有最 值是 ;它可以由抛物线
向 平移 个单位长度得到.
已知抛物线 经过点 .
将上述抛物线向下平移 个单位长度,求所得抛物线的解析式;
若点 为抛物线 上一点,直线 轴于 ,,
沿 轴平移抛物线 ,使之经过点 ,求平移后所得抛物
线的解析式.
1
2
课后作业
同课章节目录
