人教版九年级数学上册22.1.3二次函数y=a(x-h)?+k的图象和性质 第4课时教学课件(共24张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.1.3二次函数y=a(x-h)?+k的图象和性质 第4课时教学课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
二次函数 的图象和性质
(第四课时)
温故知新
二次函数的图象的顶点坐标为 ,对称轴为 .
若,当 时,有最 值 ;
当 时,随的增大而减小;当 时,随的增大而增大.
若,当 时,有最 值 ;
当 时,随的增大而减小;当 时,随的增大而增大.
小
大
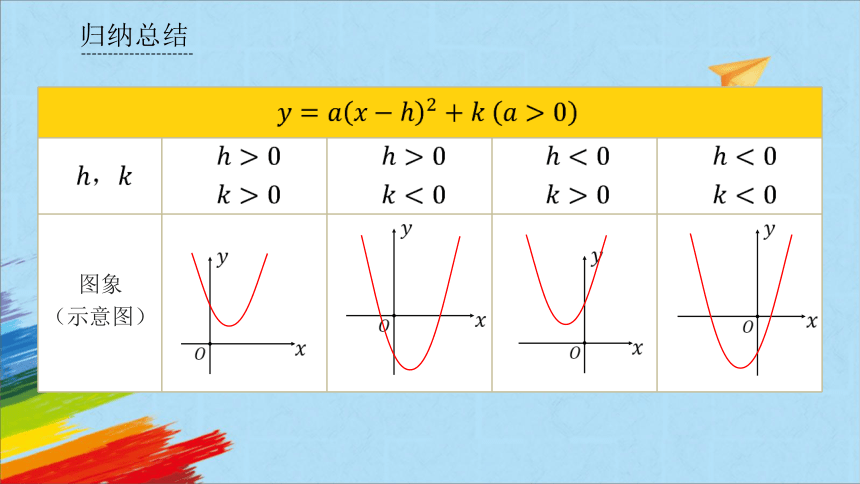
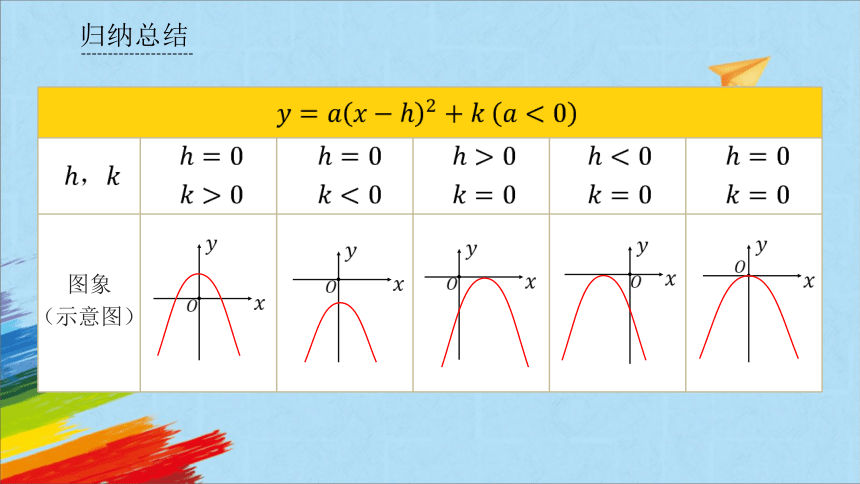
归纳总结
图象
(示意图)
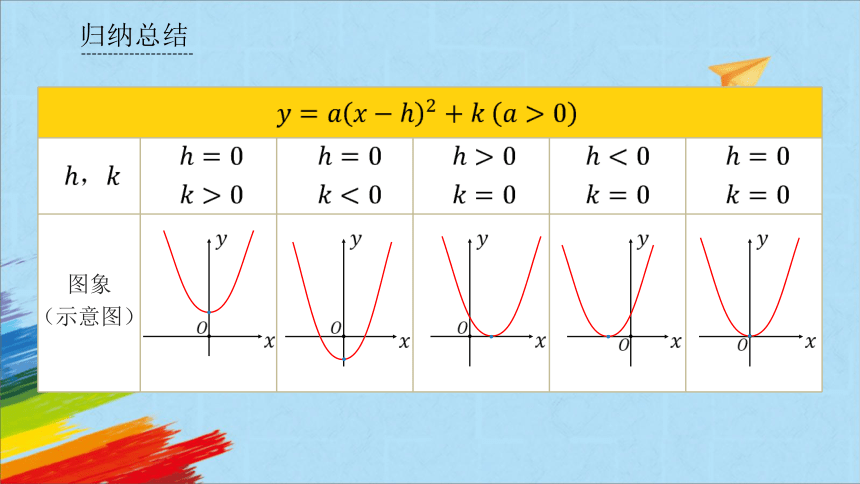
归纳总结
图象
(示意图)
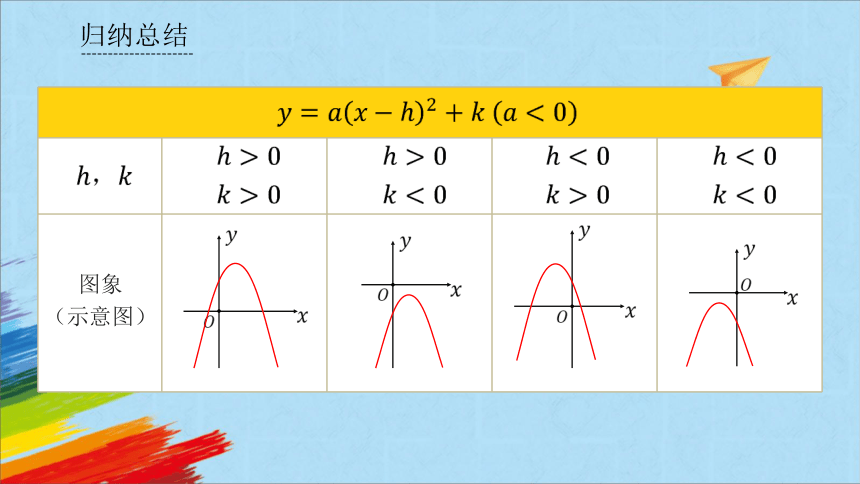
归纳总结
图象
(示意图)
归纳总结
图象
(示意图)
归纳总结
增减性
随 的增大而减小
随 的增大而增大
随 的增大而增大
随 的增大而减小
开口方向
开口向上
开口向下
开口大小
对称性
仅由决定,越大,开口越小
关于成轴对称
探究思考
在平面直角坐标系中,抛物线经过怎样的变换可以得到抛物线?
例1
向右平移个单位长度,向下平移个单位长度得到抛物线;
故抛物线向左平移个单位长度,向上平移个单位长度得到抛物线
逆向思考
解:
探究思考
在平面直角坐标系中,抛物线经过怎样的变换可以得到抛物线?
向右平移个单位长度,向上平移个单位长度得到抛物线;
再向右平移个单位长度,向上平移个单位长度得到抛物线
解:
变式1
向右平移个单位长度,
向上平移个单位长度.
用作为连接平移前后两条抛物线的桥梁.
分析
探究思考
在平面直角坐标系中,抛物线经过怎样的变换可以得到抛物线?
向左平移个单位长度,向下平移个单位长度得到抛物线;
再向右平移个单位长度,向上平移个单位长度得到抛物线
解:
变式2
向右平移个单位长度,
向下平移个单位长度.
用作为连接平移前后两条抛物线的桥梁.
分析
探究思考
在平面直角坐标系中,抛物线经过怎样的变换可以得到抛物线?
向左平移个单位长度,向下平移个单位长度得到抛物线;
再向右平移个单位长度,向上平移个单位长度得到抛物线
解:
变式2
向右平移个单位长度,
向下平移个单位长度.
还有别的方法吗
探究思考
在平面直角坐标系中,抛物线经过怎样的变换可以得到抛物线?
抛物线抛物线形状相同,位置不同.
的顶点坐标为
的顶点坐标为
解:
向右平移个单位长度,向下平移个单位长度.
变式2
选择特殊点,通常选择抛物线顶点.
分析
探究思考
在平面直角坐标系中,抛物线经过怎样的变换可以得到抛物线?
只需考虑顶点的平移
变式2
抛物线抛物线形状相同,位置不同.
的顶点坐标为
的顶点坐标为
解:
向右平移个单位长度,向下平移个单位长度.
探究思考
抛物线平移到抛物线,只需考虑如何将顶点由平移到.
总结
探究思考
已知一条抛物线的开口大小和方向均与相同,顶点坐标为,求抛物线表示的二次函数.
例2
由题目条件,
.
解:
探究思考
已知抛物线的顶点为,且经过点,求抛物线表示的二次函数.
变式1
由题目条件,
解:
探究思考
已知抛物线经平移后通过原点,且关于对称,求抛物线表示的二次函数.
变式2
由题目条件,
解:
总结
探究思考
求解抛物线对应的二次函数解析式的一类问题步骤:
设要求的二次函数为
根据题目条件确定中一项或几项的值;
1
利用待定系数法求余下的字母系数的值.
2
3
常见条件:
平移前后解析式;
对称轴;
最值;
顶点坐标
抛物线形状;
等等。
探究思考
设,,是抛物线上的三点,判断的大小关系.
例3
代入计算得
解:
探究思考
设,,是抛物线上的三点,判断的大小关系.
例3
抛物线的对称轴为当时,随的增大而增大.
.
解:
探究思考
设,,是抛物线上的三点,判断的大小关系.
变式
抛物线的对称轴为,
点的对称点的坐标为.
当时,随的增大而减小.
解:
,
探究思考
比较函数值大小一类问题步骤:
利用抛物线的对称性将要研究的点转化到对称轴的同一侧;
利用二次函数的增减性进行比较.
1
2
总结
课
堂
小
结
二次函数 的图象的平移问题.
求解二次的表达式.
比较二次函数图象上点的纵坐标大小﹒
课后作业
向左平移个单位长度,再向上平移个单位长度,得到抛物线,求的值.
二次函数的图象的顶点坐标为,且图象通过原点,求二次函数的表达式.
设,,是抛物线上的三点,判断的大小关系.
二次函数 的图象和性质
(第四课时)
温故知新
二次函数的图象的顶点坐标为 ,对称轴为 .
若,当 时,有最 值 ;
当 时,随的增大而减小;当 时,随的增大而增大.
若,当 时,有最 值 ;
当 时,随的增大而减小;当 时,随的增大而增大.
小
大
归纳总结
图象
(示意图)
归纳总结
图象
(示意图)
归纳总结
图象
(示意图)
归纳总结
图象
(示意图)
归纳总结
增减性
随 的增大而减小
随 的增大而增大
随 的增大而增大
随 的增大而减小
开口方向
开口向上
开口向下
开口大小
对称性
仅由决定,越大,开口越小
关于成轴对称
探究思考
在平面直角坐标系中,抛物线经过怎样的变换可以得到抛物线?
例1
向右平移个单位长度,向下平移个单位长度得到抛物线;
故抛物线向左平移个单位长度,向上平移个单位长度得到抛物线
逆向思考
解:
探究思考
在平面直角坐标系中,抛物线经过怎样的变换可以得到抛物线?
向右平移个单位长度,向上平移个单位长度得到抛物线;
再向右平移个单位长度,向上平移个单位长度得到抛物线
解:
变式1
向右平移个单位长度,
向上平移个单位长度.
用作为连接平移前后两条抛物线的桥梁.
分析
探究思考
在平面直角坐标系中,抛物线经过怎样的变换可以得到抛物线?
向左平移个单位长度,向下平移个单位长度得到抛物线;
再向右平移个单位长度,向上平移个单位长度得到抛物线
解:
变式2
向右平移个单位长度,
向下平移个单位长度.
用作为连接平移前后两条抛物线的桥梁.
分析
探究思考
在平面直角坐标系中,抛物线经过怎样的变换可以得到抛物线?
向左平移个单位长度,向下平移个单位长度得到抛物线;
再向右平移个单位长度,向上平移个单位长度得到抛物线
解:
变式2
向右平移个单位长度,
向下平移个单位长度.
还有别的方法吗
探究思考
在平面直角坐标系中,抛物线经过怎样的变换可以得到抛物线?
抛物线抛物线形状相同,位置不同.
的顶点坐标为
的顶点坐标为
解:
向右平移个单位长度,向下平移个单位长度.
变式2
选择特殊点,通常选择抛物线顶点.
分析
探究思考
在平面直角坐标系中,抛物线经过怎样的变换可以得到抛物线?
只需考虑顶点的平移
变式2
抛物线抛物线形状相同,位置不同.
的顶点坐标为
的顶点坐标为
解:
向右平移个单位长度,向下平移个单位长度.
探究思考
抛物线平移到抛物线,只需考虑如何将顶点由平移到.
总结
探究思考
已知一条抛物线的开口大小和方向均与相同,顶点坐标为,求抛物线表示的二次函数.
例2
由题目条件,
.
解:
探究思考
已知抛物线的顶点为,且经过点,求抛物线表示的二次函数.
变式1
由题目条件,
解:
探究思考
已知抛物线经平移后通过原点,且关于对称,求抛物线表示的二次函数.
变式2
由题目条件,
解:
总结
探究思考
求解抛物线对应的二次函数解析式的一类问题步骤:
设要求的二次函数为
根据题目条件确定中一项或几项的值;
1
利用待定系数法求余下的字母系数的值.
2
3
常见条件:
平移前后解析式;
对称轴;
最值;
顶点坐标
抛物线形状;
等等。
探究思考
设,,是抛物线上的三点,判断的大小关系.
例3
代入计算得
解:
探究思考
设,,是抛物线上的三点,判断的大小关系.
例3
抛物线的对称轴为当时,随的增大而增大.
.
解:
探究思考
设,,是抛物线上的三点,判断的大小关系.
变式
抛物线的对称轴为,
点的对称点的坐标为.
当时,随的增大而减小.
解:
,
探究思考
比较函数值大小一类问题步骤:
利用抛物线的对称性将要研究的点转化到对称轴的同一侧;
利用二次函数的增减性进行比较.
1
2
总结
课
堂
小
结
二次函数 的图象的平移问题.
求解二次的表达式.
比较二次函数图象上点的纵坐标大小﹒
课后作业
向左平移个单位长度,再向上平移个单位长度,得到抛物线,求的值.
二次函数的图象的顶点坐标为,且图象通过原点,求二次函数的表达式.
设,,是抛物线上的三点,判断的大小关系.
同课章节目录
