人教版九年级数学上册22.1.4二次函数y=ax?+bx+c的图象和性质》第2课时教学课件(共49张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.1.4二次函数y=ax?+bx+c的图象和性质》第2课时教学课件(共49张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 00:00:00 | ||
图片预览


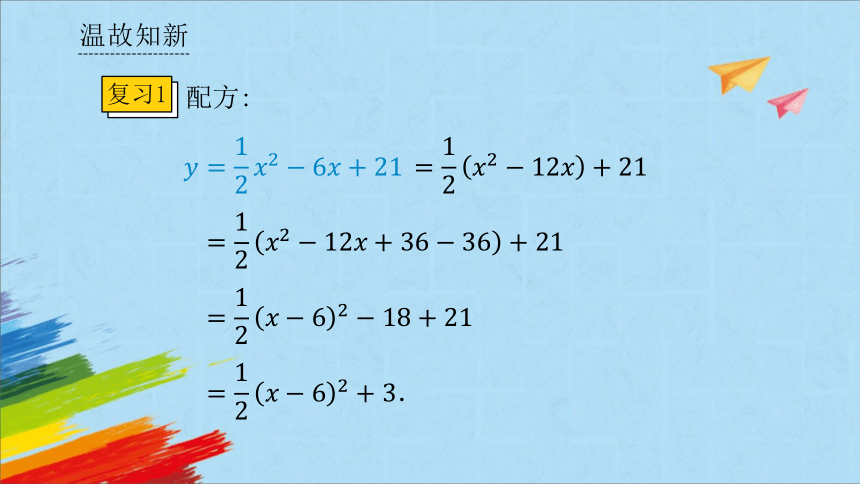



文档简介
(共49张PPT)
(第二课时)
二次函数
的图象和性质
引入新知
已知函数 的图象和性质,怎样利用这些知识讨论二次函数 的图象和性质?
思考
先以二次函数 例.
配方
温故知新
复习1
配方:
温故知新
复习2
二次函数 的图象特征.
二次函数 的图象是一条抛物线,开口 ,对称轴是 ,顶点坐标 ,顶点是抛物线的 .
向上
最低点
温故知新
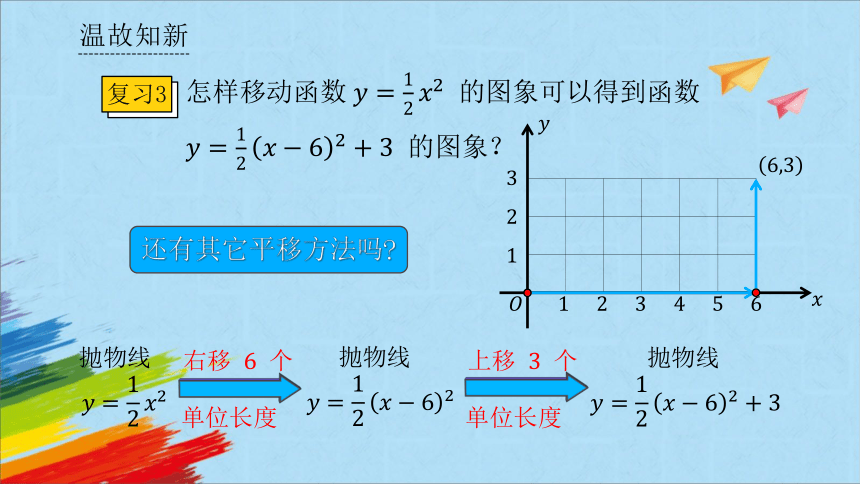
复习3
怎样移动函数 的图象可以得到函数 的图象?
抛物线
右移 个
单位长度
抛物线
上移 个
单位长度
抛物线
还有其它平移方法吗
温故知新
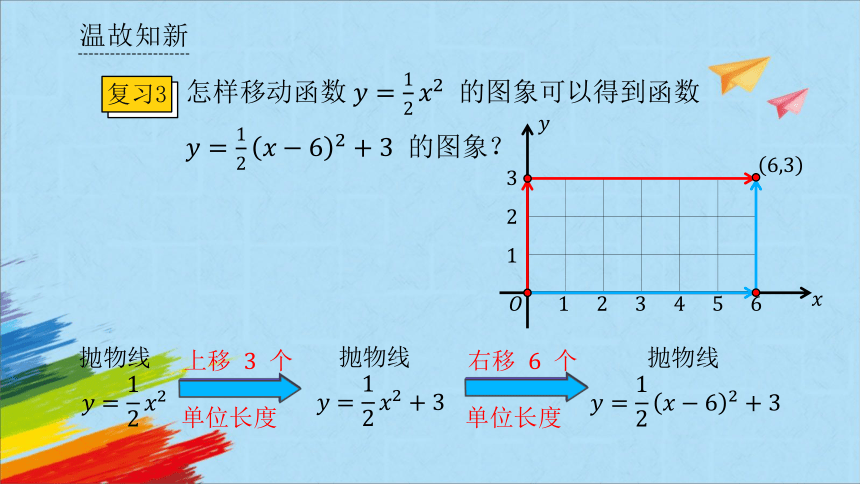
复习3
怎样移动函数 的图象可以得到函数 的图象?
抛物线
上移 个
单位长度
抛物线
右移 个
单位长度
抛物线
温故知新
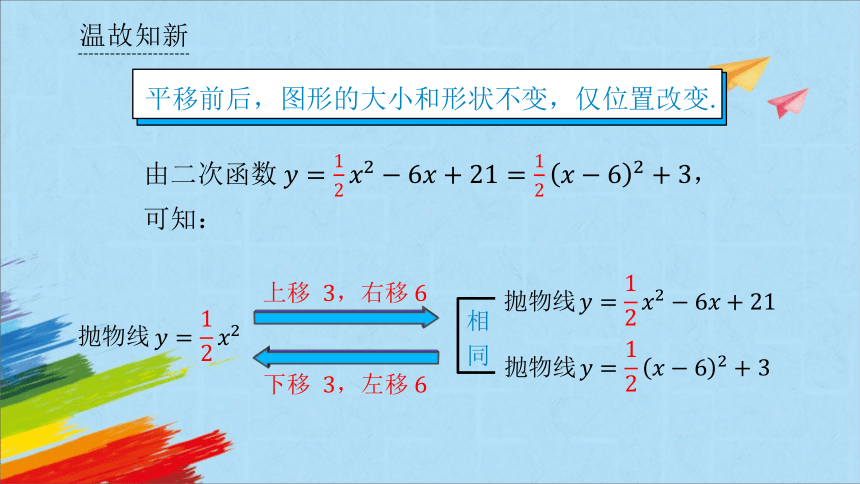
由二次函数
:
平移前后,图形的大小和形状不变,仅位置改变.
抛物线
上移 右移
抛物线
抛物线
相同
下移 左移
学习新知
在实际画图中,平移的方法不易操作,那么采取什么方法可以直接画出函数的图象呢
描点法
思考
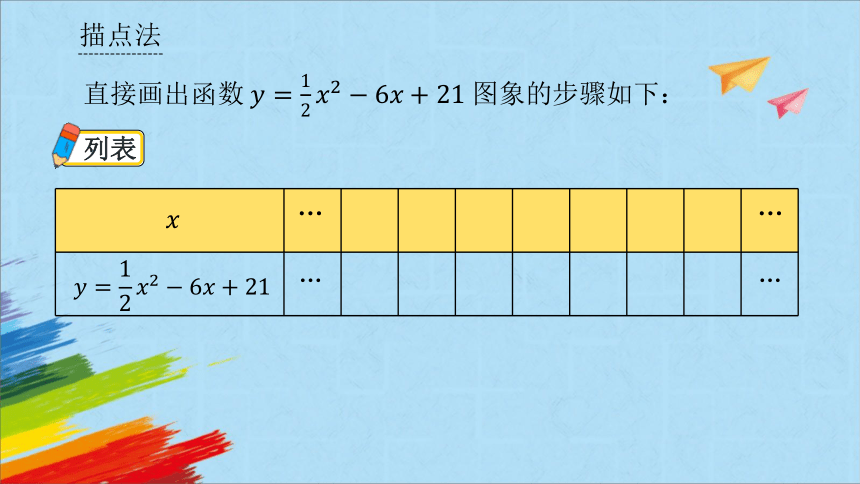
描点法
直接画出函数图象的步骤如下:
…
…
…
…
列表
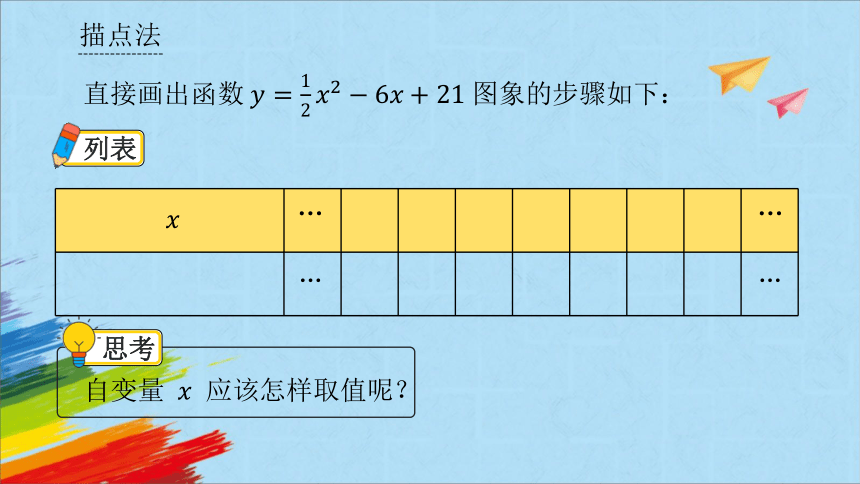
描点法
直接画出函数图象的步骤如下:
…
…
…
…
思考
自变量 应该怎样取值呢?
列表
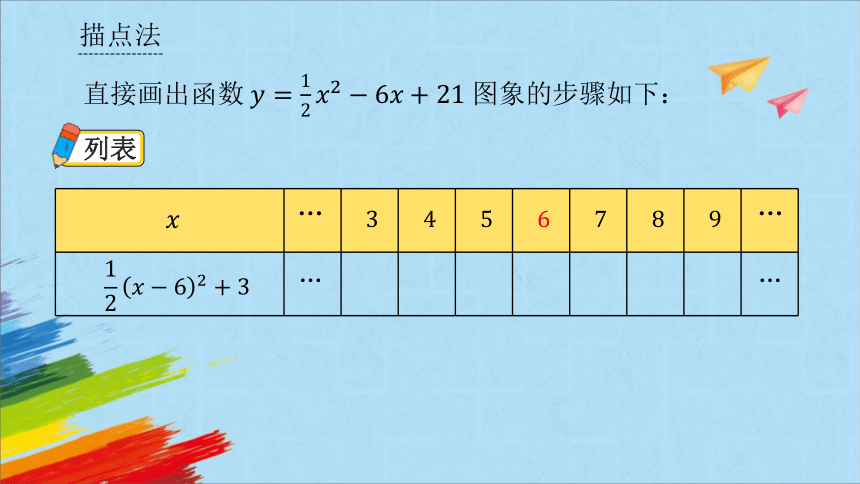
描点法
直接画出函数图象的步骤如下:
…
…
…
…
列表
描点法
直接画出函数图象的步骤如下:
…
…
…
…
列表
描点法
直接画出函数图象的步骤如下:
…
…
…
…
列表
描点
描点法
直接画出函数图象的步骤如下:
列表
描点
描点法
直接画出函数图象的步骤如下:
列表
描点
连线
描点法
二次函数图象特征:
抛物线
开口 ,对称轴是 ,顶点坐标 ,顶点是抛物线的 .
向上
最低点
描点法
二次函数图象特征:
在对称轴的左侧,
抛物线从左到右下降;
在对称轴的右侧,
抛物线从左到右上升.
描点法
二次函数图象特征:
当 ,
随 的增大而减小;
当 ,
随 的增大而增大.
当 ,
最小值
当 在 左右对称取值时,对应的函数值相等.
知识小结
两个二次函数如果二次项系数相同,那么抛物线的形状相同,可通过平移相互得到.
抛物线
抛物线
平移
平移
图象的对称性
列表
转化
描点法
图象特征 函数性质 顶点 开口方向 最值
对称轴 曲线趋势 增
减
性
图象特征 函数性质 顶点 开口方向 向上 最值
对称轴 曲线趋势 增
减
性
图象特征 函数性质 顶点 开口方向 向上 最值
对称轴 曲线趋势 增
减
性
图象特征 函数性质 顶点 开口方向 向上 最值
对称轴 曲线趋势 增
减
性
当 ,
最小值
图象特征 函数性质 顶点 开口方向 向上 最值
对称轴 直线 曲线趋势 增
减
性
当 ,
最小值
当 ,
随 的增大而减小;
当 ,
随 的增大而增大.
在对称轴的左侧,
图象从左到右下降;
在对称轴的右侧,
图象从左到右上升.
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
由配方结果知,此抛物线开口向下,对称轴是,顶点是,顶点是图象的最高点.
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
由配方结果知,此抛物线开口向下,对称轴是,顶点是,顶点是图象的最高点.
画图
先根据图象的对称性列表:
…
…
…
…
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
由配方结果知,此抛物线开口向下,对称轴是,顶点是,顶点是图象的最高点.
画图
先根据图象的对称性列表:
…
…
…
…
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
由配方结果知,此抛物线开口向下,对称轴是,顶点是,顶点是图象的最高点.
画图
先根据图象的对称性列表:
…
…
…
…
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
画图
先根据图象的对称性列表;
描点
连线
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
由配方结果知,此抛物线开口向下,对称轴是顶点是,顶点是图象的最高点.
在对称轴的左侧,
抛物线从左到右上升;
在对称轴的右侧,
抛物线从左到右下降.
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
由配方结果知,此抛物线开口向下,对称轴是顶点是,顶点是图象的最高点.
当 ,
随 的增大而增大;
当 ,
随 的增大而减小.
图象特征 函数性质 顶点 开口方向 最值
对称轴 曲线趋势 增
减
性
图象特征 函数性质 顶点 开口方向 向下 最值
对称轴 曲线趋势 增
减
性
图象特征 函数性质 顶点 开口方向 向下 最值
对称轴 曲线趋势 增
减
性
图象特征 函数性质 顶点 开口方向 向下 最值
对称轴 曲线趋势 增
减
性
当 ,
最小值
图象特征 函数性质 顶点 开口方向 向下 最值
对称轴 直线 曲线趋势 增
减
性
当 ,
随 的增大而增大;
当 ,
随 的增大而减小.
在对称轴的左侧,
抛物线从左到右上升;
在对称轴的右侧,
抛物线从左到右下降.
当 ,
最小值
要想讨论一般的二次函数的图象和性质,应该先 .
配方
知识归纳
知识归纳
要想讨论一般的二次函数的图象和性质,应该先配方,得:
是最高点还是最低点呢?由谁决定呢?
知识归纳
要对一般的二次函数的正负分类讨论对应的图象和性质.
如果 , 的性质:
此时函数有最小值.
知识归纳
要对一般的二次函数的正负分类讨论对应的图象和性质.
如果 , 的性质:
此时函数有最大值.
.
知识小结
抛物线
列表
图象的对称性
转化
描点法
提升练习
写出下列抛物线的开口方向、对称轴和顶点.
练习
1
2
3
4
提升练习
写出下列抛物线的开口方向、对称轴和顶点.
练习
1
提升练习
写出下列抛物线的开口方向、对称轴和顶点.
练习
2
提升练习
写出下列抛物线的开口方向、对称轴和顶点.
练习
3
提升练习
写出下列抛物线的开口方向、对称轴和顶点.
练习
4
当 时, 值是 ;
课后作业
填空:
已知函数
其图象是由抛物线 向 平移 个单位长度,再向 平移 个单位长度得到;
它的开口方向 ,对称轴为 ,顶点坐标 ;
当 时,
.
课后作业
已知函数
其图象是由抛物线 向 平移 个单位长度,再向 平移 个单位长度得到;
它的开口方向 ,对称轴为 ,顶点坐标 ;
当 时,
当 时, 值是 ;
.
填空:
(第二课时)
二次函数
的图象和性质
引入新知
已知函数 的图象和性质,怎样利用这些知识讨论二次函数 的图象和性质?
思考
先以二次函数 例.
配方
温故知新
复习1
配方:
温故知新
复习2
二次函数 的图象特征.
二次函数 的图象是一条抛物线,开口 ,对称轴是 ,顶点坐标 ,顶点是抛物线的 .
向上
最低点
温故知新
复习3
怎样移动函数 的图象可以得到函数 的图象?
抛物线
右移 个
单位长度
抛物线
上移 个
单位长度
抛物线
还有其它平移方法吗
温故知新
复习3
怎样移动函数 的图象可以得到函数 的图象?
抛物线
上移 个
单位长度
抛物线
右移 个
单位长度
抛物线
温故知新
由二次函数
:
平移前后,图形的大小和形状不变,仅位置改变.
抛物线
上移 右移
抛物线
抛物线
相同
下移 左移
学习新知
在实际画图中,平移的方法不易操作,那么采取什么方法可以直接画出函数的图象呢
描点法
思考
描点法
直接画出函数图象的步骤如下:
…
…
…
…
列表
描点法
直接画出函数图象的步骤如下:
…
…
…
…
思考
自变量 应该怎样取值呢?
列表
描点法
直接画出函数图象的步骤如下:
…
…
…
…
列表
描点法
直接画出函数图象的步骤如下:
…
…
…
…
列表
描点法
直接画出函数图象的步骤如下:
…
…
…
…
列表
描点
描点法
直接画出函数图象的步骤如下:
列表
描点
描点法
直接画出函数图象的步骤如下:
列表
描点
连线
描点法
二次函数图象特征:
抛物线
开口 ,对称轴是 ,顶点坐标 ,顶点是抛物线的 .
向上
最低点
描点法
二次函数图象特征:
在对称轴的左侧,
抛物线从左到右下降;
在对称轴的右侧,
抛物线从左到右上升.
描点法
二次函数图象特征:
当 ,
随 的增大而减小;
当 ,
随 的增大而增大.
当 ,
最小值
当 在 左右对称取值时,对应的函数值相等.
知识小结
两个二次函数如果二次项系数相同,那么抛物线的形状相同,可通过平移相互得到.
抛物线
抛物线
平移
平移
图象的对称性
列表
转化
描点法
图象特征 函数性质 顶点 开口方向 最值
对称轴 曲线趋势 增
减
性
图象特征 函数性质 顶点 开口方向 向上 最值
对称轴 曲线趋势 增
减
性
图象特征 函数性质 顶点 开口方向 向上 最值
对称轴 曲线趋势 增
减
性
图象特征 函数性质 顶点 开口方向 向上 最值
对称轴 曲线趋势 增
减
性
当 ,
最小值
图象特征 函数性质 顶点 开口方向 向上 最值
对称轴 直线 曲线趋势 增
减
性
当 ,
最小值
当 ,
随 的增大而减小;
当 ,
随 的增大而增大.
在对称轴的左侧,
图象从左到右下降;
在对称轴的右侧,
图象从左到右上升.
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
由配方结果知,此抛物线开口向下,对称轴是,顶点是,顶点是图象的最高点.
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
由配方结果知,此抛物线开口向下,对称轴是,顶点是,顶点是图象的最高点.
画图
先根据图象的对称性列表:
…
…
…
…
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
由配方结果知,此抛物线开口向下,对称轴是,顶点是,顶点是图象的最高点.
画图
先根据图象的对称性列表:
…
…
…
…
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
由配方结果知,此抛物线开口向下,对称轴是,顶点是,顶点是图象的最高点.
画图
先根据图象的对称性列表:
…
…
…
…
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
画图
先根据图象的对称性列表;
描点
连线
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
由配方结果知,此抛物线开口向下,对称轴是顶点是,顶点是图象的最高点.
在对称轴的左侧,
抛物线从左到右上升;
在对称轴的右侧,
抛物线从左到右下降.
巩固练习
例1
请讨论二次函数的图象和性质.
解:
配方得
由配方结果知,此抛物线开口向下,对称轴是顶点是,顶点是图象的最高点.
当 ,
随 的增大而增大;
当 ,
随 的增大而减小.
图象特征 函数性质 顶点 开口方向 最值
对称轴 曲线趋势 增
减
性
图象特征 函数性质 顶点 开口方向 向下 最值
对称轴 曲线趋势 增
减
性
图象特征 函数性质 顶点 开口方向 向下 最值
对称轴 曲线趋势 增
减
性
图象特征 函数性质 顶点 开口方向 向下 最值
对称轴 曲线趋势 增
减
性
当 ,
最小值
图象特征 函数性质 顶点 开口方向 向下 最值
对称轴 直线 曲线趋势 增
减
性
当 ,
随 的增大而增大;
当 ,
随 的增大而减小.
在对称轴的左侧,
抛物线从左到右上升;
在对称轴的右侧,
抛物线从左到右下降.
当 ,
最小值
要想讨论一般的二次函数的图象和性质,应该先 .
配方
知识归纳
知识归纳
要想讨论一般的二次函数的图象和性质,应该先配方,得:
是最高点还是最低点呢?由谁决定呢?
知识归纳
要对一般的二次函数的正负分类讨论对应的图象和性质.
如果 , 的性质:
此时函数有最小值.
知识归纳
要对一般的二次函数的正负分类讨论对应的图象和性质.
如果 , 的性质:
此时函数有最大值.
.
知识小结
抛物线
列表
图象的对称性
转化
描点法
提升练习
写出下列抛物线的开口方向、对称轴和顶点.
练习
1
2
3
4
提升练习
写出下列抛物线的开口方向、对称轴和顶点.
练习
1
提升练习
写出下列抛物线的开口方向、对称轴和顶点.
练习
2
提升练习
写出下列抛物线的开口方向、对称轴和顶点.
练习
3
提升练习
写出下列抛物线的开口方向、对称轴和顶点.
练习
4
当 时, 值是 ;
课后作业
填空:
已知函数
其图象是由抛物线 向 平移 个单位长度,再向 平移 个单位长度得到;
它的开口方向 ,对称轴为 ,顶点坐标 ;
当 时,
.
课后作业
已知函数
其图象是由抛物线 向 平移 个单位长度,再向 平移 个单位长度得到;
它的开口方向 ,对称轴为 ,顶点坐标 ;
当 时,
当 时, 值是 ;
.
填空:
同课章节目录
