人教版九年级数学上册22.1.2二次函数y=ax?的图象和性质 第1课时教学课件(共18张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.1.2二次函数y=ax?的图象和性质 第1课时教学课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 22:15:10 | ||
图片预览



文档简介
(共18张PPT)
二次函数 2 的
图象和性质
(第一课时)
一次函数 是常数,
二次函数 是常数,
一次函数
二次函数中有 三个常数,其中 ,但 和 没有限制,即 和 可以等于 ,因此二次函数必须有二次项 ,但可以没有一次项 和常数项 .
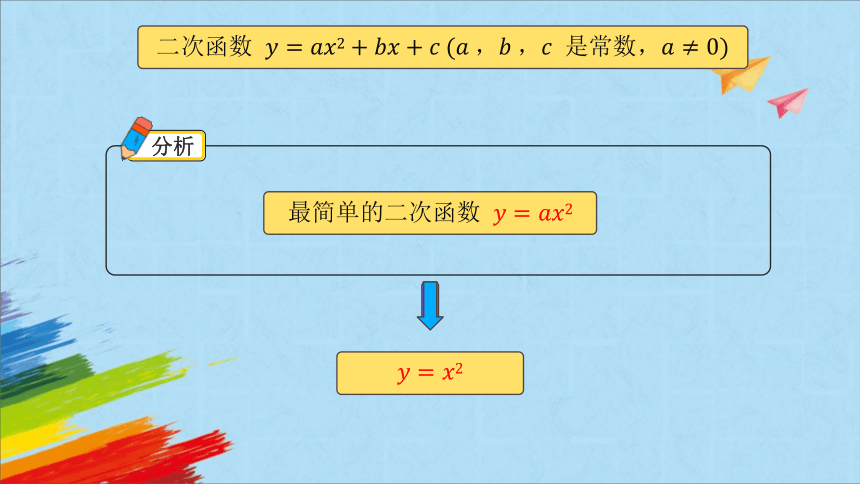
二次函数 是常数,
最简单的二次函数
分析
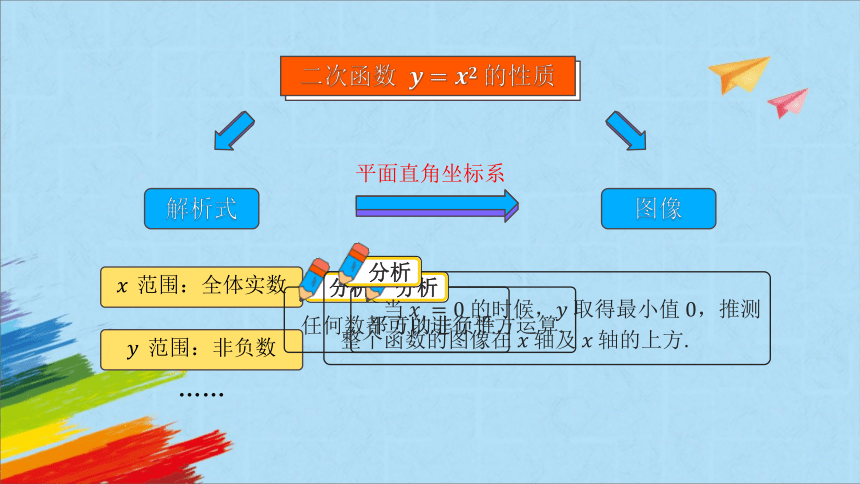
二次函数 的性质
解析式
平面直角坐标系
范围:全体实数
范围:非负数
分析
任何数都可以进行平方运算.
分析
平方的非负性.
……
图像
分析
当 的时候, 取得最小值 ,推测整个函数的图像在 轴及 轴的上方.
列表
表中给出一些自变量的值及其对应的函数值;
描点法画图步骤:
描点法画的图象
描点
在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
连线
按照横坐标由小到大的顺序把所描出的各点用平滑的曲线顺次连接起来.
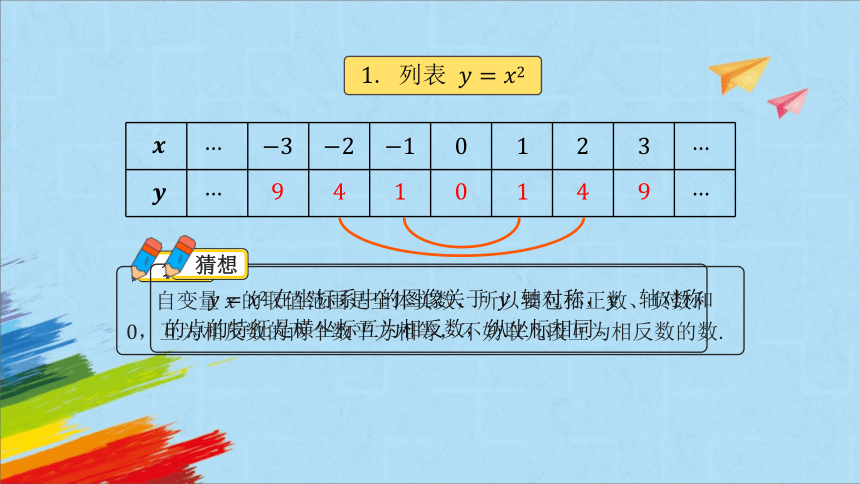
. 列表
···
···
···
···
分析
自变量 的取值范围是全体实数,所以要包括正数、负数和,互为相反数的两个数平方相等,不妨取几段互为相反数的数.
猜想
在坐标系中的图像关于 轴对称, 轴对称的点的特征是横坐标互为相反数,纵坐标相同。
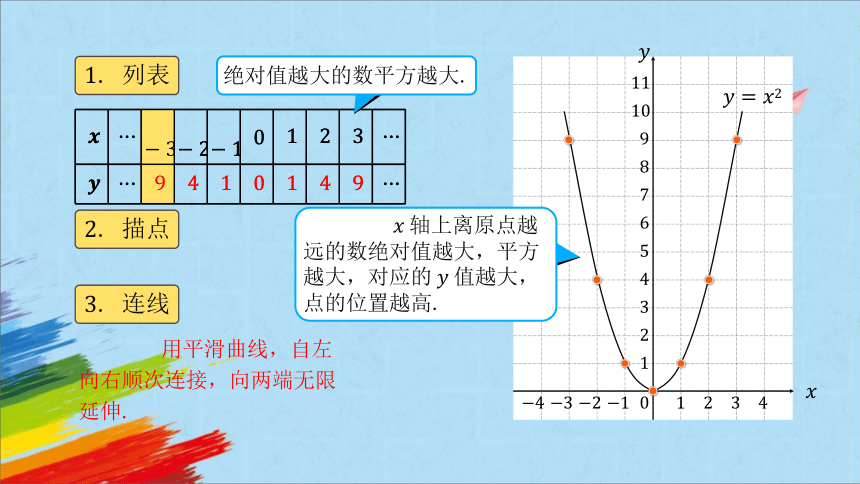
. 列表
. 描点
. 连线
用平滑曲线,自左向右顺次连接,向两端无限延伸.
绝对值越大的数平方越大.
轴上离原点越远的数绝对值越大,平方越大,对应的值越大,点的位置越高.
. 列表
. 描点
. 连线
用平滑曲线,自左向右顺次连接,向两端无限延伸.
观察函数 的图象,总结性质
是一条曲线,类似抛物在空中经过的路线,叫做抛物线;
取值关于原点对称时, 值相同——抛物线 关于 轴对称;
抛物线 与对称轴 的交点 叫抛物线 的顶点,它是抛物线 的最低点;
1
2
在对称轴左侧,抛物线 从左到右下降;
时, 随 增大而减小;
时, ;
在对称轴右侧,抛物线 从左到右上升;
时, 随 增大而增大;
时, .
3
观察函数 的图象,总结性质
符号语言
符号语言
的图像和性质
文字语言 图形/符号语言
取值范围
取值范围
图象
开口 对称轴
顶点
最值
全体实数
非负数
抛物线
向上
轴
原点
最小值(最低点)
的图像和性质
文字语言 图形/符号语言
在对称轴左侧,抛物线从左到右下降;
时, 随 增大而减小;
当
在对称轴右侧,抛物线从左到右上升;
时, 随 增大而增大;
当 时,
分析
把这个点的横坐标代入到函数的解析式中,从而求出纵坐标.
例题与练习
函数 的图象上有三点 ,比较 的大小关系.
将 分别代入函数解析式,求出 ,进而比出大小.
解法.代数法:
解法.根据函数的对称性和增减性:
函数的图象过 也过 ,因,故 .
对称轴是
分析
比大小可以考虑二次函数的增减性,但二次函数的增减性在对称轴左右两侧是不一样.
解法.图像法:
函数 的图象上有三点 ,比较 的大小关系.
解法.图像法:
例题与练习
画出函数 的图象,找到横坐标分别为 的三个点,比较其纵坐标大小(位置高低).
函数 的图象上有三点 ,比较 的大小关系.
巩固落实
将 分别代入函数解析式,求出 进而比出大小.
解法.代数法:
解法.根据函数的对称性和增减性:
函数的图象过 也过 ,因,故 .
解法.图像法:
画出函数 的图象,找到横坐标分别为 的三个点,比较其纵坐标大小(位置高低).
课
堂
小
结
相对于 是种特殊情况 .
尝试用描点法画出 取其他值时函数的图象,
比如 等;
你能试着描述一下 对函数的图象、性质有哪些影响吗?
1
2
布置作业
抛物线 不具有的性质是( ).
1
C. 对称轴是 轴
A. 开口向上
B. 与 轴不相交
D. 最低点是坐标原点
原点
已知抛物线 ,当 时,求 的取值范围.
布置作业
2
分析
直接把 等于 和 代入解析式中,求出来的并不是这一段对应着 的取值范围.
当 时,
的取值范围
二次函数 2 的
图象和性质
(第一课时)
一次函数 是常数,
二次函数 是常数,
一次函数
二次函数中有 三个常数,其中 ,但 和 没有限制,即 和 可以等于 ,因此二次函数必须有二次项 ,但可以没有一次项 和常数项 .
二次函数 是常数,
最简单的二次函数
分析
二次函数 的性质
解析式
平面直角坐标系
范围:全体实数
范围:非负数
分析
任何数都可以进行平方运算.
分析
平方的非负性.
……
图像
分析
当 的时候, 取得最小值 ,推测整个函数的图像在 轴及 轴的上方.
列表
表中给出一些自变量的值及其对应的函数值;
描点法画图步骤:
描点法画的图象
描点
在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
连线
按照横坐标由小到大的顺序把所描出的各点用平滑的曲线顺次连接起来.
. 列表
···
···
···
···
分析
自变量 的取值范围是全体实数,所以要包括正数、负数和,互为相反数的两个数平方相等,不妨取几段互为相反数的数.
猜想
在坐标系中的图像关于 轴对称, 轴对称的点的特征是横坐标互为相反数,纵坐标相同。
. 列表
. 描点
. 连线
用平滑曲线,自左向右顺次连接,向两端无限延伸.
绝对值越大的数平方越大.
轴上离原点越远的数绝对值越大,平方越大,对应的值越大,点的位置越高.
. 列表
. 描点
. 连线
用平滑曲线,自左向右顺次连接,向两端无限延伸.
观察函数 的图象,总结性质
是一条曲线,类似抛物在空中经过的路线,叫做抛物线;
取值关于原点对称时, 值相同——抛物线 关于 轴对称;
抛物线 与对称轴 的交点 叫抛物线 的顶点,它是抛物线 的最低点;
1
2
在对称轴左侧,抛物线 从左到右下降;
时, 随 增大而减小;
时, ;
在对称轴右侧,抛物线 从左到右上升;
时, 随 增大而增大;
时, .
3
观察函数 的图象,总结性质
符号语言
符号语言
的图像和性质
文字语言 图形/符号语言
取值范围
取值范围
图象
开口 对称轴
顶点
最值
全体实数
非负数
抛物线
向上
轴
原点
最小值(最低点)
的图像和性质
文字语言 图形/符号语言
在对称轴左侧,抛物线从左到右下降;
时, 随 增大而减小;
当
在对称轴右侧,抛物线从左到右上升;
时, 随 增大而增大;
当 时,
分析
把这个点的横坐标代入到函数的解析式中,从而求出纵坐标.
例题与练习
函数 的图象上有三点 ,比较 的大小关系.
将 分别代入函数解析式,求出 ,进而比出大小.
解法.代数法:
解法.根据函数的对称性和增减性:
函数的图象过 也过 ,因,故 .
对称轴是
分析
比大小可以考虑二次函数的增减性,但二次函数的增减性在对称轴左右两侧是不一样.
解法.图像法:
函数 的图象上有三点 ,比较 的大小关系.
解法.图像法:
例题与练习
画出函数 的图象,找到横坐标分别为 的三个点,比较其纵坐标大小(位置高低).
函数 的图象上有三点 ,比较 的大小关系.
巩固落实
将 分别代入函数解析式,求出 进而比出大小.
解法.代数法:
解法.根据函数的对称性和增减性:
函数的图象过 也过 ,因,故 .
解法.图像法:
画出函数 的图象,找到横坐标分别为 的三个点,比较其纵坐标大小(位置高低).
课
堂
小
结
相对于 是种特殊情况 .
尝试用描点法画出 取其他值时函数的图象,
比如 等;
你能试着描述一下 对函数的图象、性质有哪些影响吗?
1
2
布置作业
抛物线 不具有的性质是( ).
1
C. 对称轴是 轴
A. 开口向上
B. 与 轴不相交
D. 最低点是坐标原点
原点
已知抛物线 ,当 时,求 的取值范围.
布置作业
2
分析
直接把 等于 和 代入解析式中,求出来的并不是这一段对应着 的取值范围.
当 时,
的取值范围
同课章节目录
