人教版九年级数学上册22.2二次函数与一元二次方程 第2课时教学课件(共37张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.2二次函数与一元二次方程 第2课时教学课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 00:00:00 | ||
图片预览





文档简介
(共37张PPT)
二次函数与一元二次方程
(第二课时)
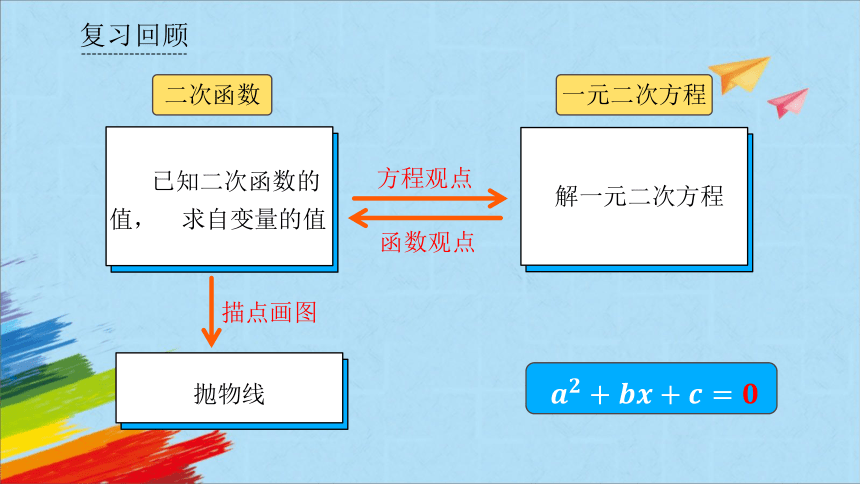
复习回顾
已知二次函数的值, 求自变量的值
解一元二次方程
方程观点
函数观点
二次函数
一元二次方程
描点画图
抛物线
探究新知
问题1
不解方程,判断下列一元二次方程根的情况.
;
, 方程有两个不相等的实数根.
, 方程有两个相等的实数根.
方程没有实数根.
探究新知
问题2
你能从函数解析式的角度解释解这三个方程的含义吗?
;
已知二次函数 的值为 ,求自变量的值;
已知二次函数 的值为 ,求自变量的值;
已知二次函数 的值为 ,求自变量的值.
探究新知
问题3
你能从函数图象的角度解释解这三个方程的含义吗?
确认抛物线 与 轴公共点的横坐标;
确认抛物线 与 轴公共点的横坐标;
确认抛物线 与 轴公共点的横坐标.
探究新知
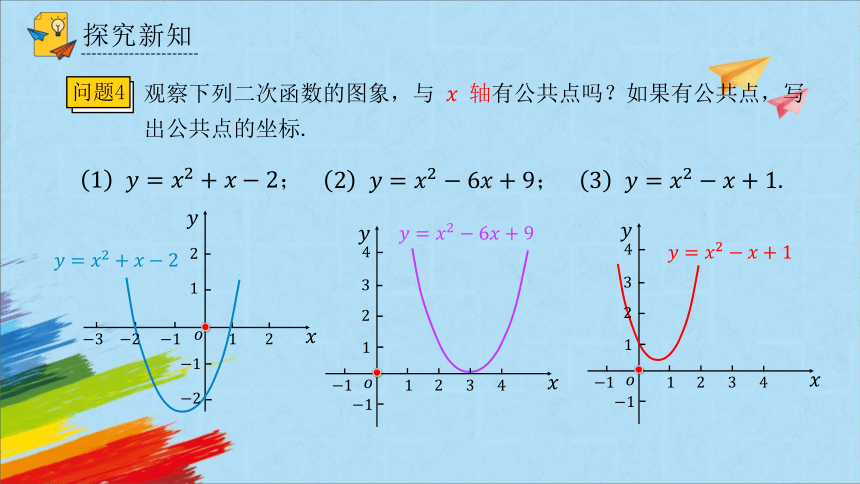
问题4
观察下列二次函数的图象,与 轴有公共点吗?如果有公共点,写出公共点的坐标.
;
探究新知
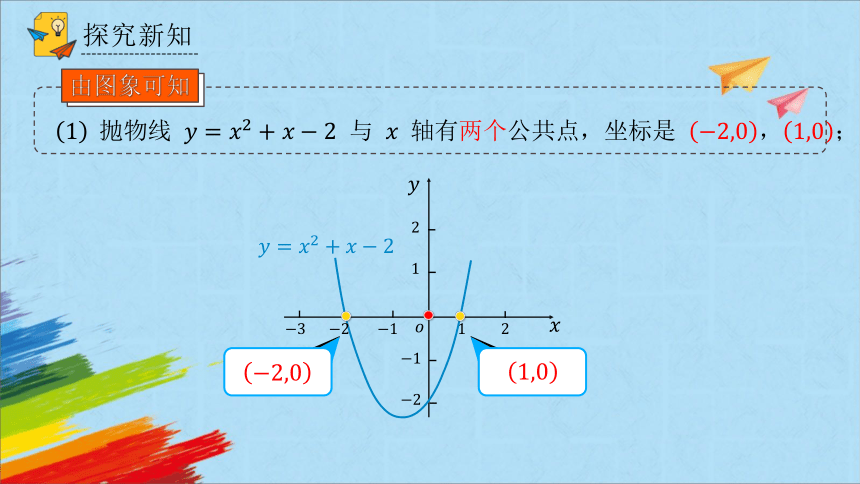
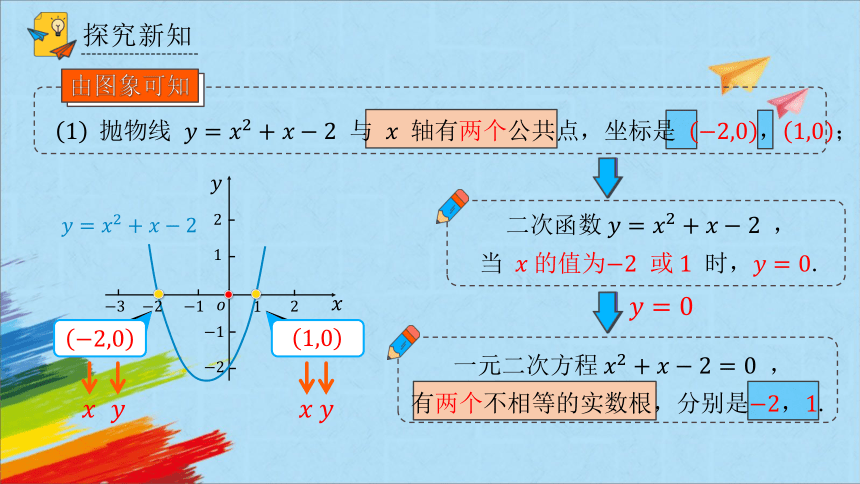
与 轴有两个公共点,坐标是 ;
由图象可知
探究新知
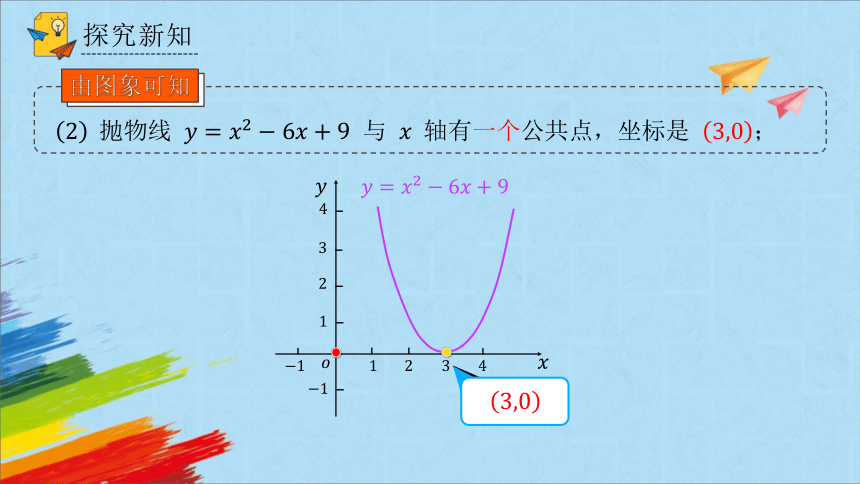
与 轴有一个公共点,坐标是 ;
由图象可知
探究新知
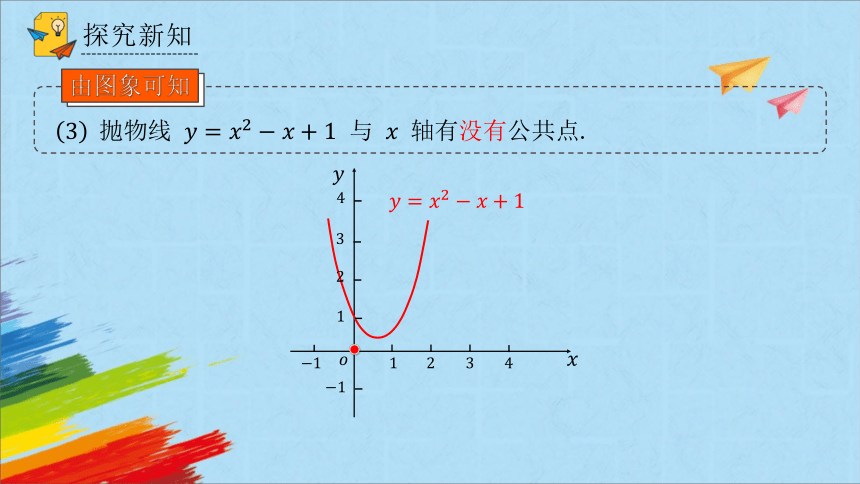
与 轴有没有公共点.
由图象可知
探究新知
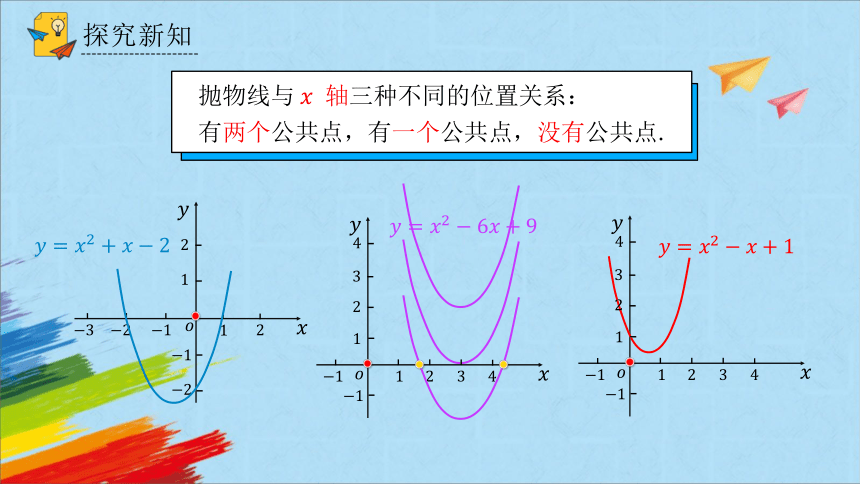
有两个公共点,有一个公共点,没有公共点.
抛物线与 轴三种不同的位置关系:
探究新知
问题5
当 取公共点的横坐标时,函数值是多少?由此你能得出相应一元二次方程的根吗?
探究新知
与 轴有两个公共点,坐标是 ;
由图象可知
二次 ,
当 的值为 或 时,.
一元二次方程 ,
有两个不相等的实数根,分别是,.
探究新知
与 轴有一个公共点,坐标是 ;
由图象可知
二次函数,
当 的值为时,.
一元二次方程,
有两个相等的实数根,是.
一元二次方程
没有实数根.
探究新知
与 轴有没有公共点.
由图象可知
二次函数 ,
当 取任何实数时,不等于 .
探究新知
从二次函数 图象可得如下结论
一元
抛物线
与轴位置关系有三种:
有两个公共点,
有一个公共点,
没有公共点.
根的三种情况:
有两个不相等的实数根,
有两个相等的实数根,
没有实数根.
探究新知
从二次函数 图象可得如下结论
抛物线
与 轴公共点的横坐标是
当 时,函数
的值
是方程
的一个根
探究新知
问题6
反过来,由一元二次方程根的情况,能确定相应的二次函数的图象与 轴的公共点的情况吗?
抛物线
与 轴公共点的横坐标是
当 时,函数
的值
是方程
的一个根
形
数
探究新知
从二次函数 图象可得如下结论
一元
抛物线
与轴位置关系有三种:
有两个公共点,
有一个公共点,
没有公共点.
根的三种情况:
有两个不相等的实数根,
有两个相等的实数根,
没有实数根.
探究新知
解一元二次方程
已知二次函数
的值为 ,求自变量 的值.
确定抛物线
与轴公共点的横坐标.
形
数
函数观点
方程观点
探究新知
问题7
不画图象,你能确定二次函数的图象与 轴的公共点的个数吗?
二次函数的图象与轴公共点的个数.
一元二次方程根的情况.
方程的根是
;
新知应用
1
已知二次函数 的部分图象如图所示.
方程的根是
方程的情况是
;
方程没有实数根,
则 的取值范围是 .
新知应用
已知二次函数 的部分图象如图所示.
根据函数图象信息求出函数解析式,得到 ,, 的值,再解方程.
思路:直接计算
方程的根是
;
1
方程的根是
;
新知应用
已知二次函数 的部分图象如图所示.
思路:直接看函数图象
方程 的根
抛物线
与轴公共点的横坐标
1
新知应用
已知二次函数 的部分图象如图所示.
方程的根是
;
,
1
已知二次函数 的部分图象如图所示.
方程的根的情况是
;
新知应用
解法
移项
与轴公共点个数
有两个不相等的实数根
1
已知二次函数 的部分图象如图所示.
方程的根的情况是
;
新知应用
解法
的函数值 时,
与直线公共点的横坐标
有两个不相等的实数根
1
已知二次函数 的部分图象如图所示.
方程实数根,则 的
取值范围是 .
新知应用
解法
没有实数根
与 轴没有公共点
1
已知二次函数 的部分图象如图所示.
方程实数根,则 的
取值范围是 .
新知应用
解法
没有实数根
与直线公共点
1
不画图象,判断下列二次函数的图象与轴公共点的个数.
新知应用
2
;
;
.
二次函数的图象与轴公共点的个数
一元二次方程根的情况
不画图象,判断下列二次函数的图象与轴公共点的个数.
新知应用
2
;
;
.
抛物线与轴公共点的个数
,
图象与 轴有两个公共点.
,
图象与 轴有一个公共点.
,
图象与 轴没有公共点.
新知应用
3
已知二次函数.
若抛物线与 轴有唯一公共点,求 的值;
若抛物线与 轴没有公共点,求 的取值范围;
若抛物线与 轴有两个公共点,求 的取值范围.
抛物线与轴公共点的个数
.
新知应用
3
已知二次函数.
若抛物线与 轴有唯一公共点,求 的值;
解: 抛物线与 轴有唯一公共点,
,
解得 .
抛物线与轴公共点的个数
新知应用
3
已知二次函数.
若抛物线与 轴有没有公共点,求 的取值范围;
解: 抛物线与 轴没有公共点,
,
解得 .
抛物线与轴公共点的个数
新知应用
3
已知二次函数.
若抛物线与 轴有两个公共点,求 的取值范围;
解: 抛物线与 轴有两个公共点,
,
解得 .
抛物线与轴公共点的个数
课
堂
小
结
请同学们回顾课程,思考以下问题:
二次函数的图象与轴有几种不同的位置关系?它与一元二次方程 的根的情况有什么联系?
能否不画图象判断抛物线与 轴公共点的个数?
课
堂
小
结
一元二次方程
二次函数
根得情况
抛物线与 轴的公共点情况
两个公共点 , .
一个公共点 .
没有公共点.
两个不相等的实数根,
两个相等的实数根
没有实数根.
课后作业
1
已知二次函数的图象如图.
方程的根是 ;
方程的根是 ;
若方程有两个不相
等的实数根,则 的取值范围是 .
2
如果函数的图象与 轴有公共点,那么 的取值范围是 .
二次函数与一元二次方程
(第二课时)
复习回顾
已知二次函数的值, 求自变量的值
解一元二次方程
方程观点
函数观点
二次函数
一元二次方程
描点画图
抛物线
探究新知
问题1
不解方程,判断下列一元二次方程根的情况.
;
, 方程有两个不相等的实数根.
, 方程有两个相等的实数根.
方程没有实数根.
探究新知
问题2
你能从函数解析式的角度解释解这三个方程的含义吗?
;
已知二次函数 的值为 ,求自变量的值;
已知二次函数 的值为 ,求自变量的值;
已知二次函数 的值为 ,求自变量的值.
探究新知
问题3
你能从函数图象的角度解释解这三个方程的含义吗?
确认抛物线 与 轴公共点的横坐标;
确认抛物线 与 轴公共点的横坐标;
确认抛物线 与 轴公共点的横坐标.
探究新知
问题4
观察下列二次函数的图象,与 轴有公共点吗?如果有公共点,写出公共点的坐标.
;
探究新知
与 轴有两个公共点,坐标是 ;
由图象可知
探究新知
与 轴有一个公共点,坐标是 ;
由图象可知
探究新知
与 轴有没有公共点.
由图象可知
探究新知
有两个公共点,有一个公共点,没有公共点.
抛物线与 轴三种不同的位置关系:
探究新知
问题5
当 取公共点的横坐标时,函数值是多少?由此你能得出相应一元二次方程的根吗?
探究新知
与 轴有两个公共点,坐标是 ;
由图象可知
二次 ,
当 的值为 或 时,.
一元二次方程 ,
有两个不相等的实数根,分别是,.
探究新知
与 轴有一个公共点,坐标是 ;
由图象可知
二次函数,
当 的值为时,.
一元二次方程,
有两个相等的实数根,是.
一元二次方程
没有实数根.
探究新知
与 轴有没有公共点.
由图象可知
二次函数 ,
当 取任何实数时,不等于 .
探究新知
从二次函数 图象可得如下结论
一元
抛物线
与轴位置关系有三种:
有两个公共点,
有一个公共点,
没有公共点.
根的三种情况:
有两个不相等的实数根,
有两个相等的实数根,
没有实数根.
探究新知
从二次函数 图象可得如下结论
抛物线
与 轴公共点的横坐标是
当 时,函数
的值
是方程
的一个根
探究新知
问题6
反过来,由一元二次方程根的情况,能确定相应的二次函数的图象与 轴的公共点的情况吗?
抛物线
与 轴公共点的横坐标是
当 时,函数
的值
是方程
的一个根
形
数
探究新知
从二次函数 图象可得如下结论
一元
抛物线
与轴位置关系有三种:
有两个公共点,
有一个公共点,
没有公共点.
根的三种情况:
有两个不相等的实数根,
有两个相等的实数根,
没有实数根.
探究新知
解一元二次方程
已知二次函数
的值为 ,求自变量 的值.
确定抛物线
与轴公共点的横坐标.
形
数
函数观点
方程观点
探究新知
问题7
不画图象,你能确定二次函数的图象与 轴的公共点的个数吗?
二次函数的图象与轴公共点的个数.
一元二次方程根的情况.
方程的根是
;
新知应用
1
已知二次函数 的部分图象如图所示.
方程的根是
方程的情况是
;
方程没有实数根,
则 的取值范围是 .
新知应用
已知二次函数 的部分图象如图所示.
根据函数图象信息求出函数解析式,得到 ,, 的值,再解方程.
思路:直接计算
方程的根是
;
1
方程的根是
;
新知应用
已知二次函数 的部分图象如图所示.
思路:直接看函数图象
方程 的根
抛物线
与轴公共点的横坐标
1
新知应用
已知二次函数 的部分图象如图所示.
方程的根是
;
,
1
已知二次函数 的部分图象如图所示.
方程的根的情况是
;
新知应用
解法
移项
与轴公共点个数
有两个不相等的实数根
1
已知二次函数 的部分图象如图所示.
方程的根的情况是
;
新知应用
解法
的函数值 时,
与直线公共点的横坐标
有两个不相等的实数根
1
已知二次函数 的部分图象如图所示.
方程实数根,则 的
取值范围是 .
新知应用
解法
没有实数根
与 轴没有公共点
1
已知二次函数 的部分图象如图所示.
方程实数根,则 的
取值范围是 .
新知应用
解法
没有实数根
与直线公共点
1
不画图象,判断下列二次函数的图象与轴公共点的个数.
新知应用
2
;
;
.
二次函数的图象与轴公共点的个数
一元二次方程根的情况
不画图象,判断下列二次函数的图象与轴公共点的个数.
新知应用
2
;
;
.
抛物线与轴公共点的个数
,
图象与 轴有两个公共点.
,
图象与 轴有一个公共点.
,
图象与 轴没有公共点.
新知应用
3
已知二次函数.
若抛物线与 轴有唯一公共点,求 的值;
若抛物线与 轴没有公共点,求 的取值范围;
若抛物线与 轴有两个公共点,求 的取值范围.
抛物线与轴公共点的个数
.
新知应用
3
已知二次函数.
若抛物线与 轴有唯一公共点,求 的值;
解: 抛物线与 轴有唯一公共点,
,
解得 .
抛物线与轴公共点的个数
新知应用
3
已知二次函数.
若抛物线与 轴有没有公共点,求 的取值范围;
解: 抛物线与 轴没有公共点,
,
解得 .
抛物线与轴公共点的个数
新知应用
3
已知二次函数.
若抛物线与 轴有两个公共点,求 的取值范围;
解: 抛物线与 轴有两个公共点,
,
解得 .
抛物线与轴公共点的个数
课
堂
小
结
请同学们回顾课程,思考以下问题:
二次函数的图象与轴有几种不同的位置关系?它与一元二次方程 的根的情况有什么联系?
能否不画图象判断抛物线与 轴公共点的个数?
课
堂
小
结
一元二次方程
二次函数
根得情况
抛物线与 轴的公共点情况
两个公共点 , .
一个公共点 .
没有公共点.
两个不相等的实数根,
两个相等的实数根
没有实数根.
课后作业
1
已知二次函数的图象如图.
方程的根是 ;
方程的根是 ;
若方程有两个不相
等的实数根,则 的取值范围是 .
2
如果函数的图象与 轴有公共点,那么 的取值范围是 .
同课章节目录
