人教版九年级数学上册24.1.3弧、弦、圆心角 第2课时教学课件(共18张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.1.3弧、弦、圆心角 第2课时教学课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 22:34:05 | ||
图片预览



文档简介
(共18张PPT)
弧、弦、圆心角
(第二课时)
复习回顾
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
应用探究
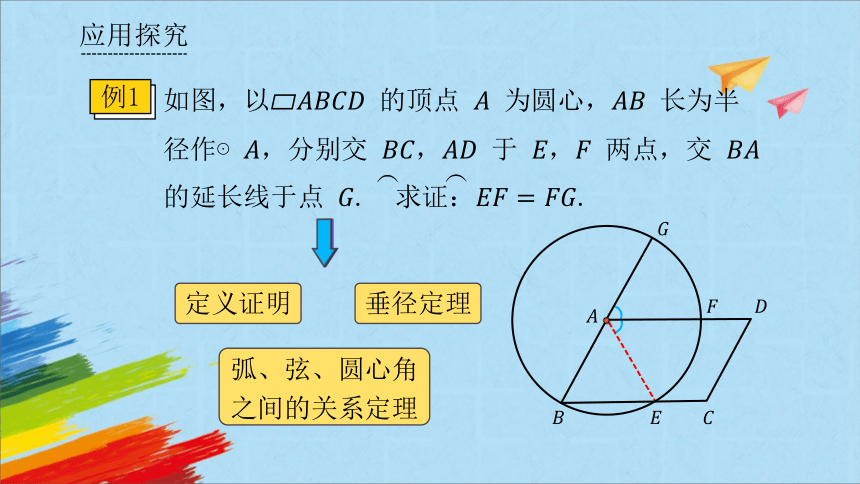
例1
如图,以 的顶点 为圆心, 长为半径作⊙,分别交 , 于 , 两点,交 的延长线于点 . 求证:.
(
(
定义证明
垂径定理
弧、弦、圆心角之间的关系定理
应用探究
证明:连接 ,
,
,
又,
,
在 中,
.
(
(
应用探究
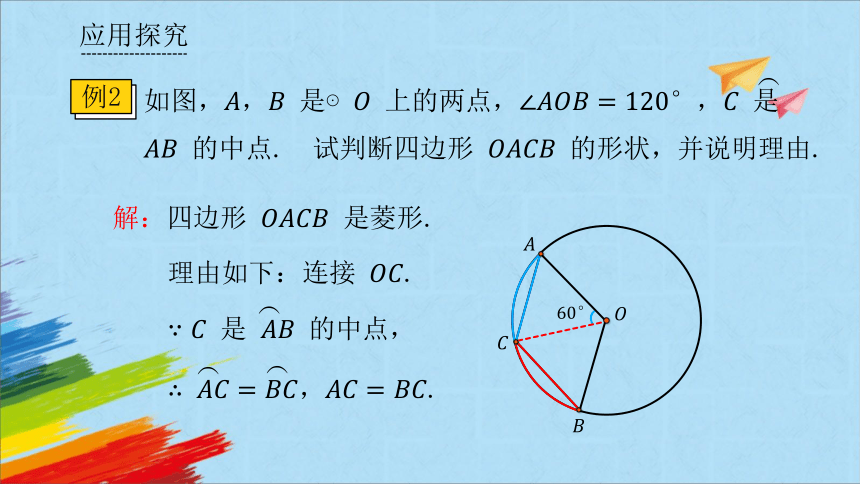
例2
如图, 是⊙ 上的两点,, 是 的中点. 试判断四边形 的形状,并说明理由.
(
解:四边形 是菱形.
理由如下:连接 .
是 的中点,
(
,.
(
(
应用探究
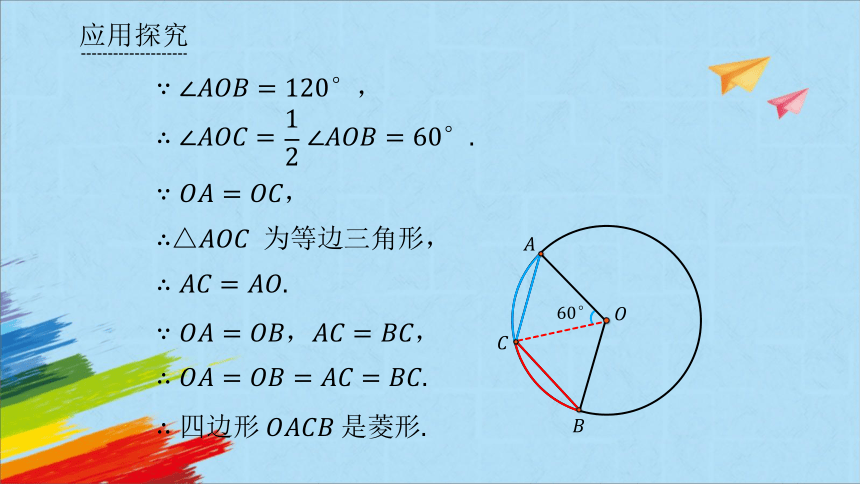
,
,
△ 为等边三角形,
,,
应用探究
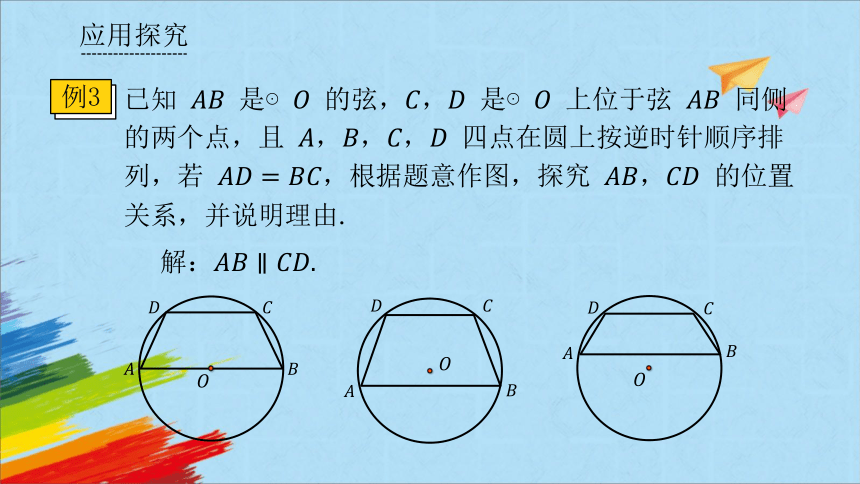
例3
已知 是⊙ 的弦,, 是⊙ 上位于弦 同侧的两个点,且 ,,, 四点在圆上按逆时针顺序排列,若 ,根据题意作图,探究 , 的位置关系,并说明理由.
应用探究
例3
已知 是⊙ 的弦,, 是⊙ 上位于弦 同侧的两个点,且 ,,, 四点在圆上按逆时针顺序排列,若 ,根据题意作图,探究 , 的位置关系,并说明理由.
当 为⊙ 的直径时,
连接 ,.
,
,
应用探究
例3
已知 是⊙ 的弦,, 是⊙ 上位于弦 同侧的两个点,且 ,,, 四点在圆上按逆时针顺序排列,若 ,根据题意作图,探究 , 的位置关系,并说明理由.
为⊙ 的直径,
应用探究
例3
已知 是⊙ 的弦,, 是⊙ 上位于弦 同侧的两个点,且 ,,, 四点在圆上按逆时针顺序排列,若 ,根据题意作图,探究 , 的位置关系,并说明理由.
当 位于圆心 的异侧时,
连接 ,,.
,
应用探究
过点 作 于点 ,交 与点 ,交 于点 .
(
,
,
应用探究
例3
已知 是⊙ 的弦,, 是⊙ 上位于弦 同侧的两个点,且 ,,, 四点在圆上按逆时针顺序排列,若 ,根据题意作图,探究 , 的位置关系,并说明理由.
当 位于圆心 的同侧时,
应用探究
例3
已知 是⊙ 的弦,, 是⊙ 上位于弦 同侧的两个点,且 ,,, 四点在圆上按逆时针顺序排列,若 ,根据题意作图,探究 , 的位置关系,并说明理由.
当 位于圆心 的同侧时,
应用探究
例4
如图,,, 为⊙ 上的三个点,如果,
那么( ).
(
(
(
(
(
(
不确定
分析
作 的角平分线 ,交 于点 .
(
(
(
(
(
(
变式
如图,,, 为⊙ 上的三个点,如果,
那么( ).
(
(
应用探究
分析
取 的中点 ,
(
(
(
(
不确定
练习
如图,已知锐角,根据以下作图过程补全图形,
有下列结论:
①;②若 ,则;
③;④.
其中所有正确结论的序号为 .
①
②
③
在射线 上取一点 ,以点 为圆心, 长为半径作 ,交射线 于点 ,连接 ;
(
分别以点 , 为圆心, 长为半径作弧,交 于点 ,,连接 ,.
(
课
堂
小
结
圆心角等
弧等
弦等
同圆或等圆中
——解决同圆或等圆中,与弧相等、角相等、线段相等相关的证明和计算问题的又一个方法.
——化归与转化的数学思想.
课后作业
1
如图,, 是⊙ 的两条直径,过点 作 ,交⊙ 于点 ,连接 ,.
求证:.
2
如图,,, 是 的三等分点, 与 , 分别交于点 ,.
求证:.
(
弧、弦、圆心角
(第二课时)
复习回顾
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
应用探究
例1
如图,以 的顶点 为圆心, 长为半径作⊙,分别交 , 于 , 两点,交 的延长线于点 . 求证:.
(
(
定义证明
垂径定理
弧、弦、圆心角之间的关系定理
应用探究
证明:连接 ,
,
,
又,
,
在 中,
.
(
(
应用探究
例2
如图, 是⊙ 上的两点,, 是 的中点. 试判断四边形 的形状,并说明理由.
(
解:四边形 是菱形.
理由如下:连接 .
是 的中点,
(
,.
(
(
应用探究
,
,
△ 为等边三角形,
,,
应用探究
例3
已知 是⊙ 的弦,, 是⊙ 上位于弦 同侧的两个点,且 ,,, 四点在圆上按逆时针顺序排列,若 ,根据题意作图,探究 , 的位置关系,并说明理由.
应用探究
例3
已知 是⊙ 的弦,, 是⊙ 上位于弦 同侧的两个点,且 ,,, 四点在圆上按逆时针顺序排列,若 ,根据题意作图,探究 , 的位置关系,并说明理由.
当 为⊙ 的直径时,
连接 ,.
,
,
应用探究
例3
已知 是⊙ 的弦,, 是⊙ 上位于弦 同侧的两个点,且 ,,, 四点在圆上按逆时针顺序排列,若 ,根据题意作图,探究 , 的位置关系,并说明理由.
为⊙ 的直径,
应用探究
例3
已知 是⊙ 的弦,, 是⊙ 上位于弦 同侧的两个点,且 ,,, 四点在圆上按逆时针顺序排列,若 ,根据题意作图,探究 , 的位置关系,并说明理由.
当 位于圆心 的异侧时,
连接 ,,.
,
应用探究
过点 作 于点 ,交 与点 ,交 于点 .
(
,
,
应用探究
例3
已知 是⊙ 的弦,, 是⊙ 上位于弦 同侧的两个点,且 ,,, 四点在圆上按逆时针顺序排列,若 ,根据题意作图,探究 , 的位置关系,并说明理由.
当 位于圆心 的同侧时,
应用探究
例3
已知 是⊙ 的弦,, 是⊙ 上位于弦 同侧的两个点,且 ,,, 四点在圆上按逆时针顺序排列,若 ,根据题意作图,探究 , 的位置关系,并说明理由.
当 位于圆心 的同侧时,
应用探究
例4
如图,,, 为⊙ 上的三个点,如果,
那么( ).
(
(
(
(
(
(
不确定
分析
作 的角平分线 ,交 于点 .
(
(
(
(
(
(
变式
如图,,, 为⊙ 上的三个点,如果,
那么( ).
(
(
应用探究
分析
取 的中点 ,
(
(
(
(
不确定
练习
如图,已知锐角,根据以下作图过程补全图形,
有下列结论:
①;②若 ,则;
③;④.
其中所有正确结论的序号为 .
①
②
③
在射线 上取一点 ,以点 为圆心, 长为半径作 ,交射线 于点 ,连接 ;
(
分别以点 , 为圆心, 长为半径作弧,交 于点 ,,连接 ,.
(
课
堂
小
结
圆心角等
弧等
弦等
同圆或等圆中
——解决同圆或等圆中,与弧相等、角相等、线段相等相关的证明和计算问题的又一个方法.
——化归与转化的数学思想.
课后作业
1
如图,, 是⊙ 的两条直径,过点 作 ,交⊙ 于点 ,连接 ,.
求证:.
2
如图,,, 是 的三等分点, 与 , 分别交于点 ,.
求证:.
(
同课章节目录
