人教版九年级数学上册23.2.3关于原点对称的点的坐标 第1课时教学课件(共42张PPT)
文档属性
| 名称 | 人教版九年级数学上册23.2.3关于原点对称的点的坐标 第1课时教学课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 22:34:59 | ||
图片预览





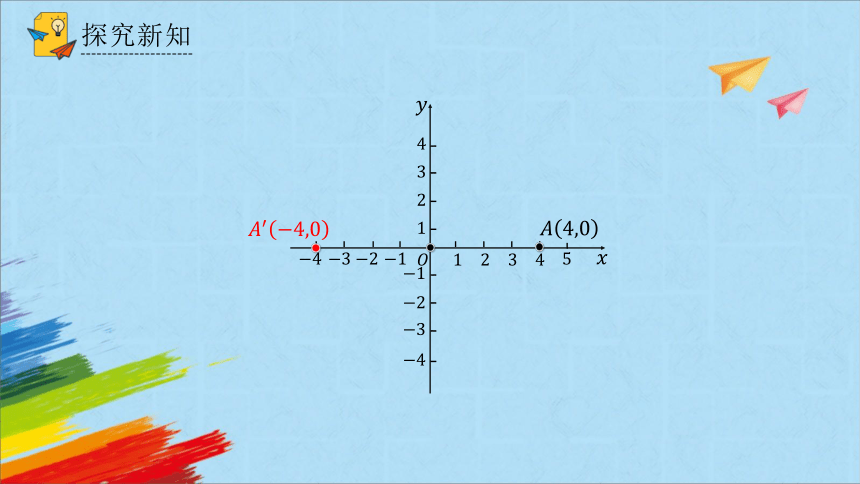
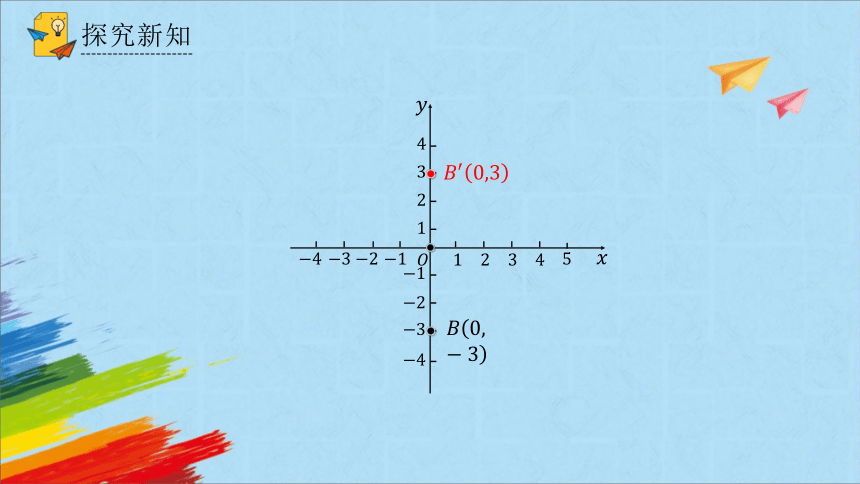
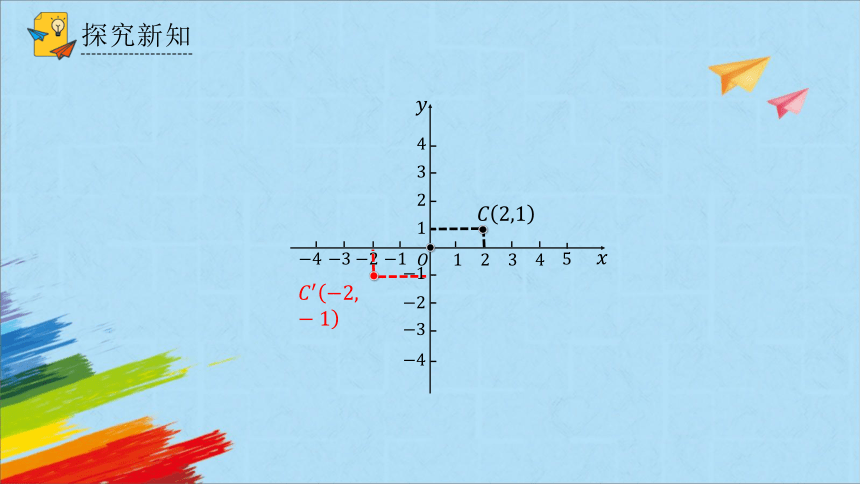


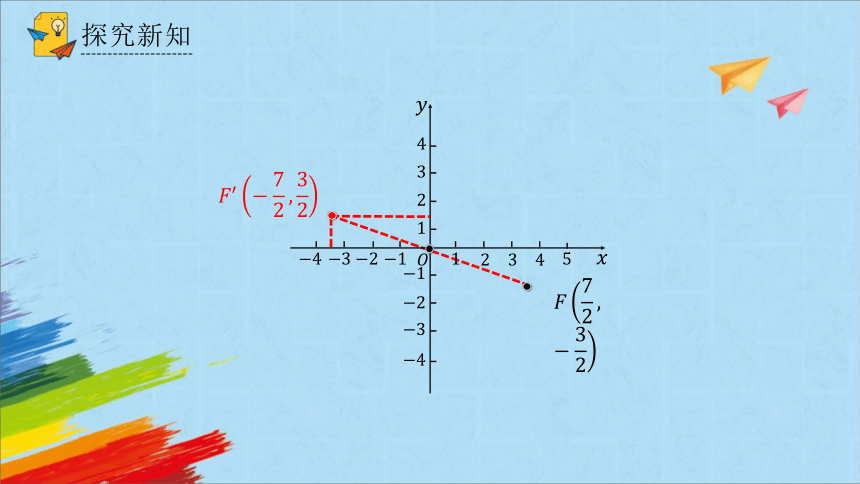
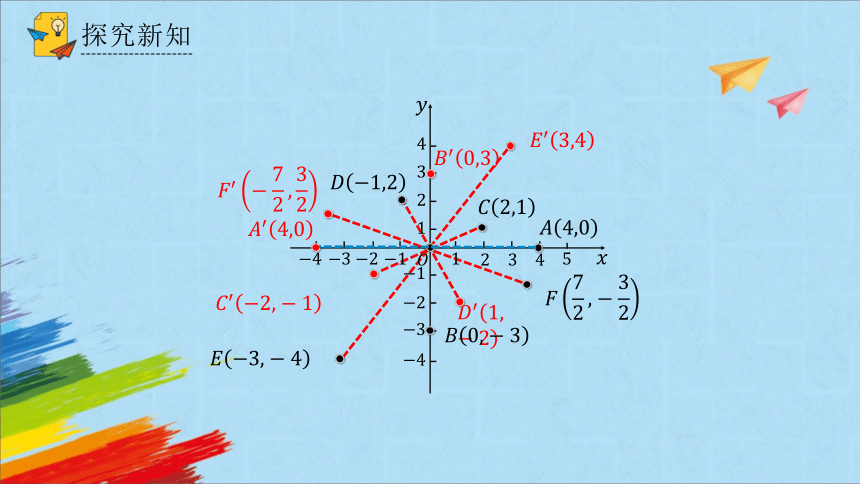
文档简介
(共42张PPT)
关于原点对称的点的坐标
(第一课时)
复习回顾
如图,画出点关于点的对称点 .
复习回顾
解:如图,连接 ,在的延长线上截取,即
可以求得点 关于点的对称点 .
引入新知
探究新知
5
如图,在直角坐标系中,作出下列已知点关于原点 的对称点,并写出它们的坐标,这些坐标与已知点的坐标有什么关系呢?
探究
探究新知
5
探究新知
5
探究新知
5
探究新知
5
探究新知
5
探究新知
5
探究新知
5
探究新知
已知点的坐标 关于原点对称后的点的坐标
探究新知
归纳
两个点关于原点对称时,它们的坐标符号相反,坐标的绝对值相等,即点关于原点的对称点为.
探究新知
探究新知
探究新知
过点 ,点 向轴作垂线,垂足分别为点 、点. 根据中心对称的性质可得 ,
分析
探究新知
过点 ,点 向轴作垂线,垂足分别为点 、点. 根据中心对称的性质可得 ,
显然,
,
那么,
可得 ,
所以点 与点 的坐标符号相反,坐标的绝对值相等.
探究新知
关于原点对称的两个点的坐标关系
两个点关于原点对称时,它们的坐标符号相反,坐标的绝对值相等,即点 关于原点的对称点为 .
例题解析
例1
如图,利用关于原点对称的点的坐标关系,作出与△关于原点对称的图形.
例题解析
例1
如图,利用关于原点对称的点的坐标关系,作出与△关于原点对称的图形.
解:点 关于原点的对称点为,因此△
的三个顶点,, 关于原点的对称点分别为 , , ,
例题解析
例1
如图,利用关于原点对称的点的坐标关系,作出与△关于原点对称的图形.
依次连接就可以得到与△ 关于原点对称的△ .
例题解析
例2
如图,已知点的坐标为,点的坐标为 ,菱形 的对角线交于坐标原点 求 , 两点的坐标.
解:因为菱形 的对角线交于坐标原点.
由菱形的性质,可得
点 与点关于原点 对称,
点与点 关于原点 对称.
例题解析
例2
点 关于原点的对称点为 ,所以,点关于原点的对称点为 ,点,关于原点的对称点为 .
如图,已知点的坐标为,点的坐标为 ,菱形 的对角线交于坐标原点 求 , 两点的坐标.
例3
已知点关于原点的对称点在第一象限,求整数 的值.
例题解析
解:点 关于原点的对称点为, 因此
关于原点的对称点为 .
由于在第一象限,因此
+5
解得
所以整数的值为 ,,.
例4
例题解析
如图,点,关于点 的对称点
求证:
分析
例4
例题解析
如图,点,关于点 的对称点
求证:
如图,过点作 轴的平行线,过点 作 轴的平行线,交于点;过点 作 轴的平行线,过点 作 轴的平行线,交于点 .
证明:
例4
例题解析
如图,点,关于点 的对称点
求证:
用坐标表示出线段的长度,可得
,
,
例4
例题解析
如图,点,关于点 的对称点
求证:
根据中心对称的性质可得 .
由于 ,,
,
,
那么.
.
例4
例题解析
如图,点,关于点 的对称点
求证:
代入,可得
,
,
化简,可得 ,
.
例题解析
例4
如图,点,关于点 的对称点
求证:
例题解析
例4
如图,点,关于点 的对称点
求证:
证明 将线段 沿着 平移,
根据平移的性质,
点 平移到 ,
点 平移到 .
另解
例题解析
例4
如图,点,关于点 的对称点
求证:
平移后点 与点 关于点 对称,
所以
,
.
化简,可得 ,
.
例题解析
例5
如图,利用例所得的结论,作出△关于点的对称的图形.
分析
设点关于 的对称点为 . 根据例 的结论,可得
,
解得 , . 即
同理,可求得点 、点 关于点 的对称点的坐标.
例题解析
例5
如图,利用例所得的结论,作出△关于点的对称的图形.
根据例所得到的结论,△ 的三个顶点,,关于的对称点为 .
解:
例题解析
依此连接 ,, ,就可以得到与△点对称的△.
例题解析
例6
已知直线,画出直线 关于原点 对称的直线 ,并求出直线的解析式.
解:
在直线 上取两点 , ,根据关于原点对称的点的坐标关系,可得点 关于原点的对称点为,点 关于原点的对称点为. 两点确定一条直线,连接,即为直线 .
例题解析
点 ,点 在直线 上,设直线 的解析式为,代入 、 的坐标,可得 , .
所以直线 的解析式为 .
例6
已知直线,画出直线 关于原点 对称的直线 ,并求出直线的解析式.
同学们解决完例 ,那能不能用类似的办法,求出一条抛物线关于原点 对称所得抛物线的解析式呢?
思考
请同学们课后思考以下问题!
课
堂
小
结
归纳
两个点关于原点对称时,它们的坐标符号相反,坐标的绝对值相等,即点关于原点的对称点为.
课后作业
下列各点中哪两个点关于原点 对称
,,,,,,.
写出下列各点关于原点的对称点, , , 的坐标:
,,,.
请同学们完成下面三道课后作业:
课后作业
请同学们完成下面三道课后作业:
写出下列各点关于点 对称点, , ,
的坐标:
,,,.
已知抛物线的解析式为,画出这条抛物线,
并求出它关于原点对称所得的抛物线的解析式.
关于原点对称的点的坐标
(第一课时)
复习回顾
如图,画出点关于点的对称点 .
复习回顾
解:如图,连接 ,在的延长线上截取,即
可以求得点 关于点的对称点 .
引入新知
探究新知
5
如图,在直角坐标系中,作出下列已知点关于原点 的对称点,并写出它们的坐标,这些坐标与已知点的坐标有什么关系呢?
探究
探究新知
5
探究新知
5
探究新知
5
探究新知
5
探究新知
5
探究新知
5
探究新知
5
探究新知
已知点的坐标 关于原点对称后的点的坐标
探究新知
归纳
两个点关于原点对称时,它们的坐标符号相反,坐标的绝对值相等,即点关于原点的对称点为.
探究新知
探究新知
探究新知
过点 ,点 向轴作垂线,垂足分别为点 、点. 根据中心对称的性质可得 ,
分析
探究新知
过点 ,点 向轴作垂线,垂足分别为点 、点. 根据中心对称的性质可得 ,
显然,
,
那么,
可得 ,
所以点 与点 的坐标符号相反,坐标的绝对值相等.
探究新知
关于原点对称的两个点的坐标关系
两个点关于原点对称时,它们的坐标符号相反,坐标的绝对值相等,即点 关于原点的对称点为 .
例题解析
例1
如图,利用关于原点对称的点的坐标关系,作出与△关于原点对称的图形.
例题解析
例1
如图,利用关于原点对称的点的坐标关系,作出与△关于原点对称的图形.
解:点 关于原点的对称点为,因此△
的三个顶点,, 关于原点的对称点分别为 , , ,
例题解析
例1
如图,利用关于原点对称的点的坐标关系,作出与△关于原点对称的图形.
依次连接就可以得到与△ 关于原点对称的△ .
例题解析
例2
如图,已知点的坐标为,点的坐标为 ,菱形 的对角线交于坐标原点 求 , 两点的坐标.
解:因为菱形 的对角线交于坐标原点.
由菱形的性质,可得
点 与点关于原点 对称,
点与点 关于原点 对称.
例题解析
例2
点 关于原点的对称点为 ,所以,点关于原点的对称点为 ,点,关于原点的对称点为 .
如图,已知点的坐标为,点的坐标为 ,菱形 的对角线交于坐标原点 求 , 两点的坐标.
例3
已知点关于原点的对称点在第一象限,求整数 的值.
例题解析
解:点 关于原点的对称点为, 因此
关于原点的对称点为 .
由于在第一象限,因此
+5
解得
所以整数的值为 ,,.
例4
例题解析
如图,点,关于点 的对称点
求证:
分析
例4
例题解析
如图,点,关于点 的对称点
求证:
如图,过点作 轴的平行线,过点 作 轴的平行线,交于点;过点 作 轴的平行线,过点 作 轴的平行线,交于点 .
证明:
例4
例题解析
如图,点,关于点 的对称点
求证:
用坐标表示出线段的长度,可得
,
,
例4
例题解析
如图,点,关于点 的对称点
求证:
根据中心对称的性质可得 .
由于 ,,
,
,
那么.
.
例4
例题解析
如图,点,关于点 的对称点
求证:
代入,可得
,
,
化简,可得 ,
.
例题解析
例4
如图,点,关于点 的对称点
求证:
例题解析
例4
如图,点,关于点 的对称点
求证:
证明 将线段 沿着 平移,
根据平移的性质,
点 平移到 ,
点 平移到 .
另解
例题解析
例4
如图,点,关于点 的对称点
求证:
平移后点 与点 关于点 对称,
所以
,
.
化简,可得 ,
.
例题解析
例5
如图,利用例所得的结论,作出△关于点的对称的图形.
分析
设点关于 的对称点为 . 根据例 的结论,可得
,
解得 , . 即
同理,可求得点 、点 关于点 的对称点的坐标.
例题解析
例5
如图,利用例所得的结论,作出△关于点的对称的图形.
根据例所得到的结论,△ 的三个顶点,,关于的对称点为 .
解:
例题解析
依此连接 ,, ,就可以得到与△点对称的△.
例题解析
例6
已知直线,画出直线 关于原点 对称的直线 ,并求出直线的解析式.
解:
在直线 上取两点 , ,根据关于原点对称的点的坐标关系,可得点 关于原点的对称点为,点 关于原点的对称点为. 两点确定一条直线,连接,即为直线 .
例题解析
点 ,点 在直线 上,设直线 的解析式为,代入 、 的坐标,可得 , .
所以直线 的解析式为 .
例6
已知直线,画出直线 关于原点 对称的直线 ,并求出直线的解析式.
同学们解决完例 ,那能不能用类似的办法,求出一条抛物线关于原点 对称所得抛物线的解析式呢?
思考
请同学们课后思考以下问题!
课
堂
小
结
归纳
两个点关于原点对称时,它们的坐标符号相反,坐标的绝对值相等,即点关于原点的对称点为.
课后作业
下列各点中哪两个点关于原点 对称
,,,,,,.
写出下列各点关于原点的对称点, , , 的坐标:
,,,.
请同学们完成下面三道课后作业:
课后作业
请同学们完成下面三道课后作业:
写出下列各点关于点 对称点, , ,
的坐标:
,,,.
已知抛物线的解析式为,画出这条抛物线,
并求出它关于原点对称所得的抛物线的解析式.
同课章节目录
