人教版九年级数学上册24.4弧长和扇形面积 第1课时教学课件(共31张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.4弧长和扇形面积 第1课时教学课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 22:35:51 | ||
图片预览




文档简介
(共31张PPT)
(第一课时)
弧长和扇形面积
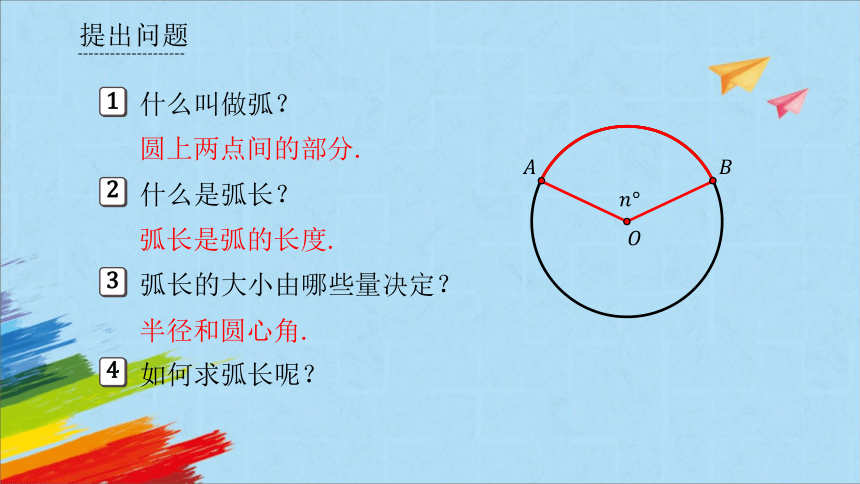
提出问题
什么叫做弧?
1
半径和圆心角.
什么是弧长?
2
弧长是弧的长度.
弧长的大小由哪些量决定?
3
如何求弧长呢?
4
圆上两点间的部分.
问题探究一
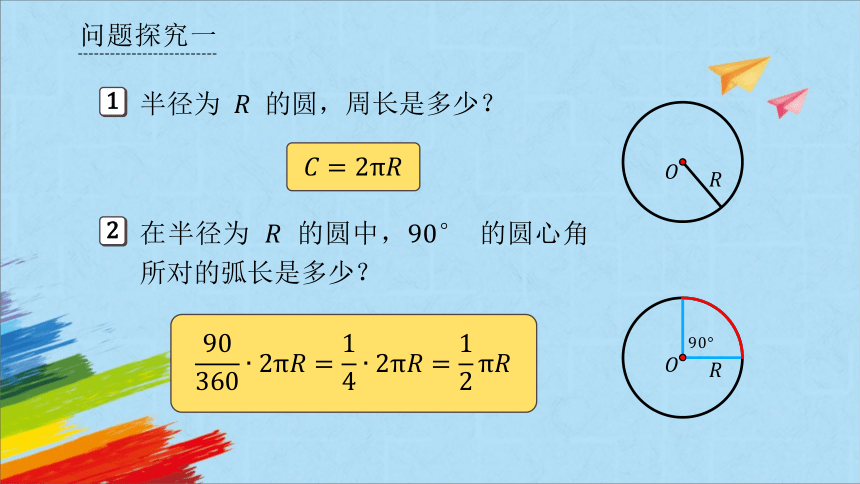
半径为 的圆,周长是多少?
1
在半径为 的圆中, 的圆心角所对的弧长是多少?
2
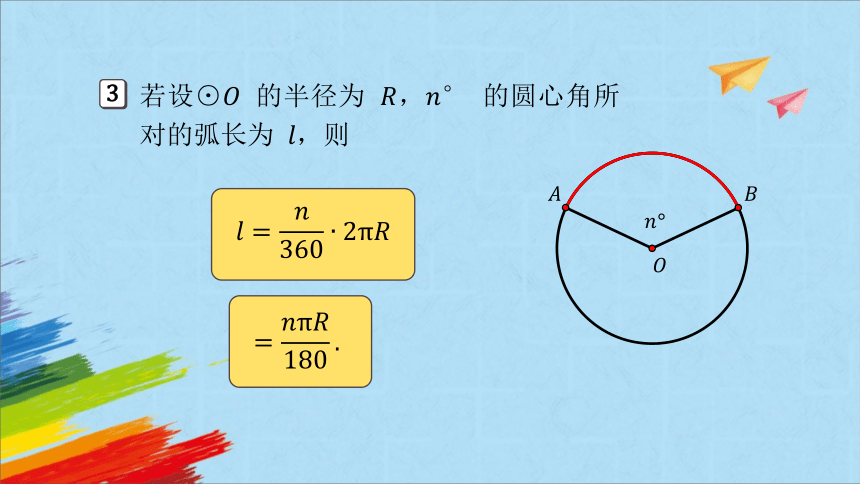
若设⊙ 的半径为 , 的圆心角所对的弧长为 ,则
3
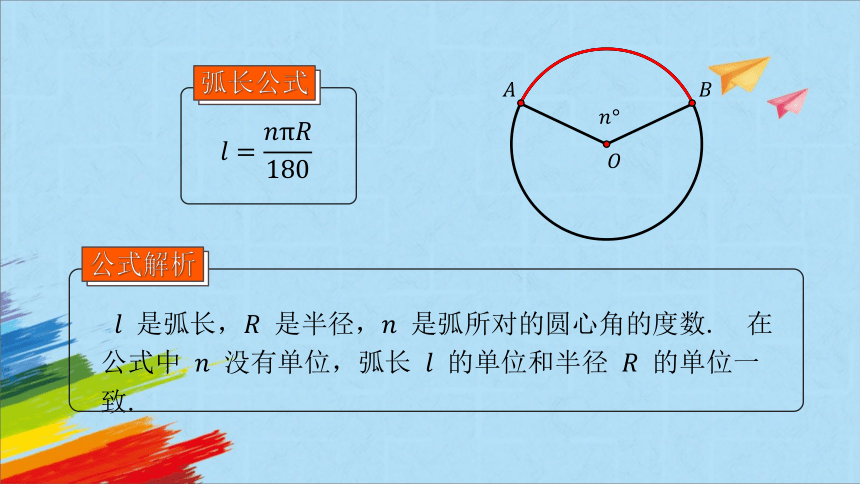
弧长公式
是弧长, 是半径, 是弧所对的圆心角的度数. 在公式中 没有单位,弧长 的单位和半径 的单位一致.
公式解析
练习
半径为 的圆中, 的圆心角所对的弧长是多少?
1
半径为的圆中,一段弧长为的弧,求它所对的圆心角的度数.
2
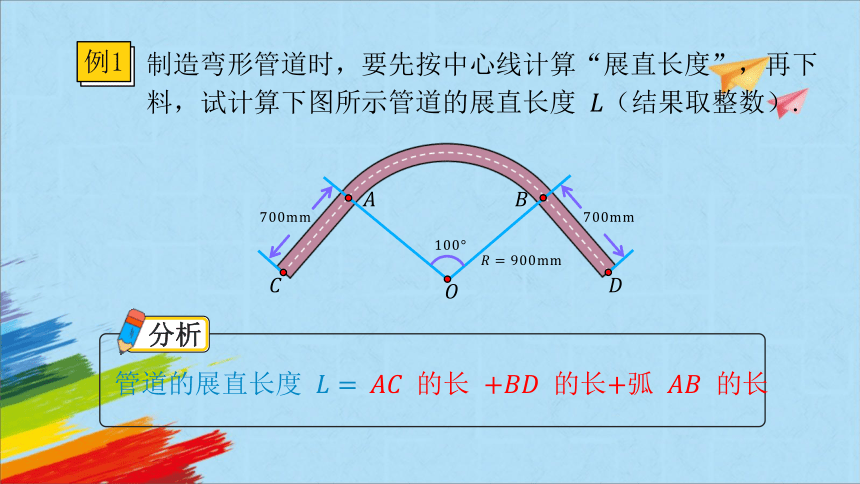
例1
制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算下图所示管道的展直长度 (结果取整数).
分析
管道的展直长度
的长 的长弧 的长
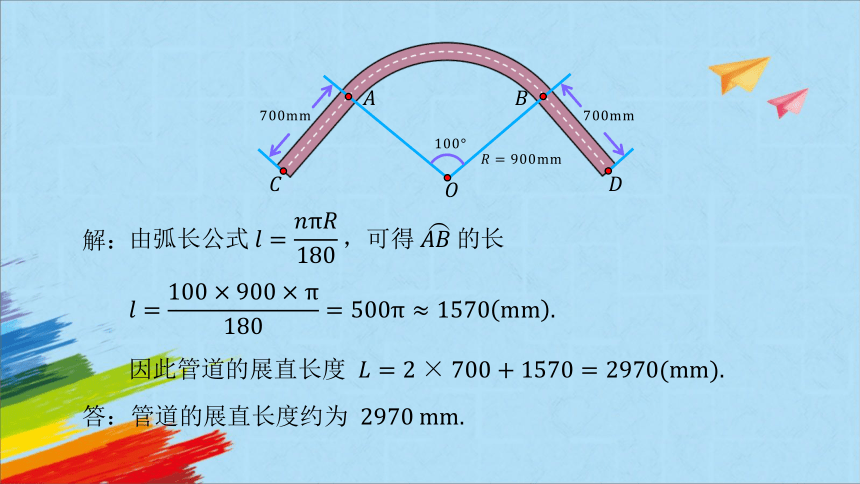
因此管道的展直长度
解:
答:管道的展直长度约为
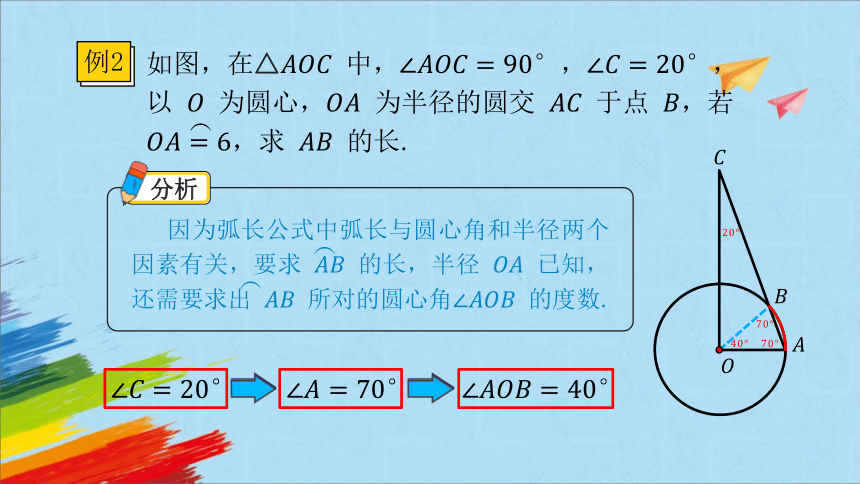
例2
如图,在△ 中,,以 为圆心, 为半径的圆交 于点 ,若 ,求 的长.
因为弧长公式中弧长与圆心角和半径两个因素有关,要求 的长,半径 已知,还需要求出 所对的圆心角 的度数.
分析
例2
如图,在△ 中,,以 为圆心, 为半径的圆交 于点 ,若 ,求 的长.
Click to edit Master title style
Click to edit Master subtitle style
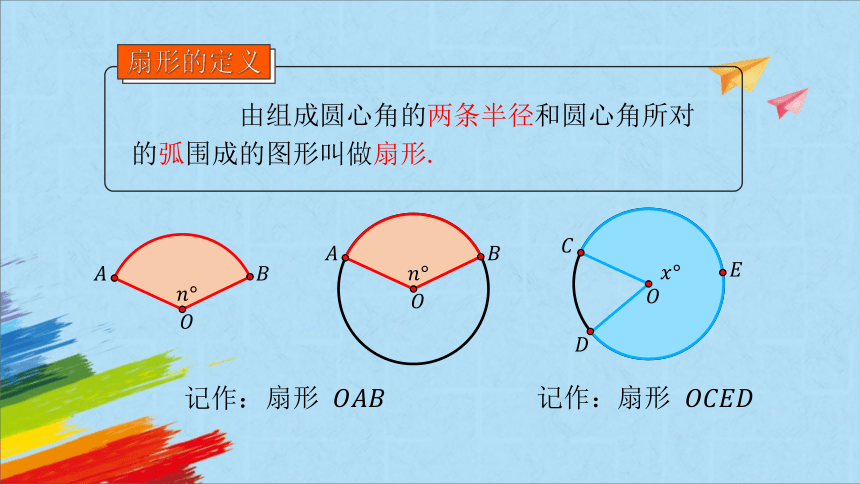
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
扇形的定义
记作:
扇形
记作:扇形
提出问题
扇形的面积由哪些量决定?
1
如何求扇形的面积呢?
2
半径和圆心角
问题探究二
半径为 的圆,面积是多少?
1
若设⊙ 的半径为 ,圆心角为 的扇形面积为 ,则
2
扇形
扇形面积公式
是扇形面积, 是半径, 是扇形圆心角的度数.
公式解析
扇形
扇形
比较扇形面积与弧长公式,用弧长表示扇形面积:
扇形
练习
已知扇形的圆心角为 ,半径为 ,则这个扇形的
1
面积 .
扇形
扇形
扇形
练习
2
半径 .
扇形
练习
3
面积为 .
扇形
扇形
例3
如图,水平放置的圆柱形排水管道的截面半径是 ,其中水面高 ,求截面上有水部分的面积(精确到 ).
弧 的中点到弦 的距离
半径
分析
有水部分的面积
扇形
扇形
半径
圆心角
特殊△
分析
有水部分的面积
扇形
底
高
半弦
△
解:
根据垂径定理, 平分 ,
连接 ,,过 作 于 ,交 于点 ,连接 .
.
.
又
.
.
从而
在△利用勾股定理,得
.
扇形
答:截面上有水部分的面积约为 .
例4
已知正三角形 的边长为 ,,, 分别为 ,, 的中点,分别以 ,, 为圆心,
分析
阴影部分面积等于正三角形面积减去 个扇形的面积.
如何求边长为 的正三角形的面积?
例4
已知正三角形 的边长为 ,,, 分别为 ,, 的中点,分别以 ,, 为圆心,
扇形
阴影
解:
课
堂
小
结
弧长和扇形面积
1
弧长和扇形面积公式是什么?
扇形
课
堂
小
结
弧长和扇形面积
2
你是如何得到这两个公式的?如何运用?
扇形
课后作业
已知扇形的圆心角为 ,半径为 ,则扇形的弧长是( ).
1
A
B
C
D
如图所示,把边长为 的正方形 的一边放在定直线上,按顺时针方向绕点 旋转到如图的位置,则点 运动到点所经过的路线长度为 .
2
课后作业
如图,在正方形 中,分别以 , 为圆心,以正方形的边长 为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的面积为 .
3
(第一课时)
弧长和扇形面积
提出问题
什么叫做弧?
1
半径和圆心角.
什么是弧长?
2
弧长是弧的长度.
弧长的大小由哪些量决定?
3
如何求弧长呢?
4
圆上两点间的部分.
问题探究一
半径为 的圆,周长是多少?
1
在半径为 的圆中, 的圆心角所对的弧长是多少?
2
若设⊙ 的半径为 , 的圆心角所对的弧长为 ,则
3
弧长公式
是弧长, 是半径, 是弧所对的圆心角的度数. 在公式中 没有单位,弧长 的单位和半径 的单位一致.
公式解析
练习
半径为 的圆中, 的圆心角所对的弧长是多少?
1
半径为的圆中,一段弧长为的弧,求它所对的圆心角的度数.
2
例1
制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算下图所示管道的展直长度 (结果取整数).
分析
管道的展直长度
的长 的长弧 的长
因此管道的展直长度
解:
答:管道的展直长度约为
例2
如图,在△ 中,,以 为圆心, 为半径的圆交 于点 ,若 ,求 的长.
因为弧长公式中弧长与圆心角和半径两个因素有关,要求 的长,半径 已知,还需要求出 所对的圆心角 的度数.
分析
例2
如图,在△ 中,,以 为圆心, 为半径的圆交 于点 ,若 ,求 的长.
Click to edit Master title style
Click to edit Master subtitle style
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
扇形的定义
记作:
扇形
记作:扇形
提出问题
扇形的面积由哪些量决定?
1
如何求扇形的面积呢?
2
半径和圆心角
问题探究二
半径为 的圆,面积是多少?
1
若设⊙ 的半径为 ,圆心角为 的扇形面积为 ,则
2
扇形
扇形面积公式
是扇形面积, 是半径, 是扇形圆心角的度数.
公式解析
扇形
扇形
比较扇形面积与弧长公式,用弧长表示扇形面积:
扇形
练习
已知扇形的圆心角为 ,半径为 ,则这个扇形的
1
面积 .
扇形
扇形
扇形
练习
2
半径 .
扇形
练习
3
面积为 .
扇形
扇形
例3
如图,水平放置的圆柱形排水管道的截面半径是 ,其中水面高 ,求截面上有水部分的面积(精确到 ).
弧 的中点到弦 的距离
半径
分析
有水部分的面积
扇形
扇形
半径
圆心角
特殊△
分析
有水部分的面积
扇形
底
高
半弦
△
解:
根据垂径定理, 平分 ,
连接 ,,过 作 于 ,交 于点 ,连接 .
.
.
又
.
.
从而
在△利用勾股定理,得
.
扇形
答:截面上有水部分的面积约为 .
例4
已知正三角形 的边长为 ,,, 分别为 ,, 的中点,分别以 ,, 为圆心,
分析
阴影部分面积等于正三角形面积减去 个扇形的面积.
如何求边长为 的正三角形的面积?
例4
已知正三角形 的边长为 ,,, 分别为 ,, 的中点,分别以 ,, 为圆心,
扇形
阴影
解:
课
堂
小
结
弧长和扇形面积
1
弧长和扇形面积公式是什么?
扇形
课
堂
小
结
弧长和扇形面积
2
你是如何得到这两个公式的?如何运用?
扇形
课后作业
已知扇形的圆心角为 ,半径为 ,则扇形的弧长是( ).
1
A
B
C
D
如图所示,把边长为 的正方形 的一边放在定直线上,按顺时针方向绕点 旋转到如图的位置,则点 运动到点所经过的路线长度为 .
2
课后作业
如图,在正方形 中,分别以 , 为圆心,以正方形的边长 为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的面积为 .
3
同课章节目录
