人教版九年级数学上册21.2.4解一元二次方程——一元二次方程的根的判别式 教学课件(共54张PPT)
文档属性
| 名称 | 人教版九年级数学上册21.2.4解一元二次方程——一元二次方程的根的判别式 教学课件(共54张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 22:39:10 | ||
图片预览




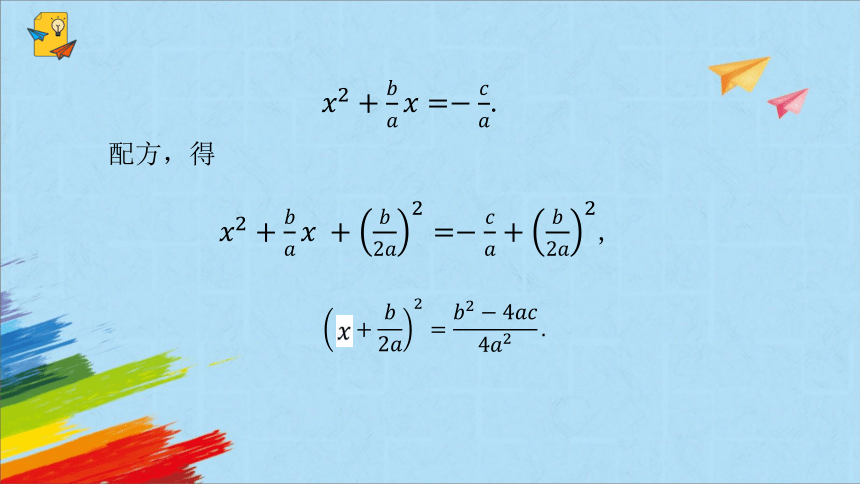







文档简介
(共54张PPT)
解一元二次方程——
一元二次方程根的判别式
(第一课时)
复习回顾
解一元二次方程的方法有:
直接开平方法,配方法,公式法,因式分解法.
1
配方法和公式法是解一元二次方程的通法.
2
思考
一元二次方程的根的情况,由哪些因素决定呢?
思考
一元二次方程求根公式的推导过程
.
解:两边同时除以,得
.
移项,得
.
.
配方,得
,
因为,所以 .
当 时, .
方程有实数根.
由于,所以 .
当 时,
.
.
取任何实数都不能使
方程无实数根.
引入新知
一般地,式子叫做一元二次方程根的判别式,通常用希腊字母“”表示它,即 .
归纳
当 时,方程有实数根;
当 时,方程没有实数根.
思考
在存在实数根的情况下,我们还能判断出实数根的什么情况呢?
思考
一元二次方程
当 这时 .
方程有两个不相等实数根.
,
.
.
当 .
,
方程有两个相等实数根.
.
一元二次方程
归纳
一元二次方程 根的情况:
当 时,方程有两个不相等的实数根;
当 时,方程有两个相等的实数根;
当 时,方程没有实数根.
归纳
不求出一元二次方程的根,判断下列方程根的情况:
例1
;
;
;
不求出一元二次方程的根,判断下列方程根的情况:
例1
;
解:
一元二次方程有两个不相等的实数根.
不求出一元二次方程的根,判断下列方程根的情况:
例1
;
解:
.
一元二次方程有两个不相等的实数根.
归纳
不解方程,判断一元二次方程根的情况的一般步骤:
归纳
;
.
不求出一元二次方程的根,判断下列方程根的情况:
例1
;
;
解:
一元二次方程有两个相等实数根.
解:
.
一元二次方程无实数根.
在不解方程的情况下,判断下列关于 的一元二次方程
根的情况.
例2
解:
分析
分析
当
分析
分析
当 时,
当时,
一元二次方程有两个不相等的实数根;
一元二次方程有两个相等的实数根.
当
分析
分析
一元二次方程有两个实数根.
当
分析
分析
一元二次方程有实数根.
当
在不解方程的情况下,判断下列关于 的一元二次方程
根的情况.
例2
解:
所以 有实数根.
在不解方程的情况下,判断下列关于 的方程
根的情况.
例3
解:
,
一元二次方程有两个不相等的实数根.
求证:不论 取何实数,关于 的一元二次方程
有两个不相等的实数根.
例4
证明:
,
一元二次方程有
两个不相等的实数根.
课
堂
小
结
1
一元二次方程根的判别式的定义.
2
一元二次方程根的判别式判别一元二次方程根的情况:
当 时,方程有两个不相等的实数根;
当 时,方程有两个相等的实数根;
当 时,方程没有实数根.
课
堂
小
结
1
一元二次方程根的判别式的定义.
2
一元二次方程根的判别式判别一元二次方程根的情况:
当 时,方程有两个实数根,
或方程有实数根;
当 时,方程没有实数根.
课后作业
1
利用判别式判断下列方程的根的情况.
,
,
.
2
在不解方程的情况下,判断关于 的一元二次方程
的情况.
3
求证:不论 取何实数,关于 的方程
有实数根.
解一元二次方程——
一元二次方程根的判别式
(第二课时)
复习回顾
一元二次方程
.
当 时,方程有两个不相等的实数根;
当 时,方程有两个相等的实数根;
当 时,方程没有实数根.
引入新知
一元二次方程
,
方程有两个不相等的实数根,则;
方程有两个相等的实数根,则;
方程没有实数根,则.
由一元二次方程求根公式的推导过程可知
,
当 时,方程的实数根为
引入新知
一元二次方程
,
方程有两个不相等的实数根,则;
方程有两个相等的实数根,则;
方程没有实数根,则.
例1
如果关于 的一元二次方程 ,
有两个不相等的实数根,求 的取值范围.
解:
.
,
.
.
变式1
如果关于 的一元二次方程 ,
有两个不相等的实数根,求 的取值范围.
变式2
如果关于 的一元二次方程 ,
没有实数根,求 的取值范围.
变式1
如果关于 的一元二次方程 ,
有两个不相等的实数根,求 的取值范围.
解:
0.
变式2
如果关于 的一元二次方程 ,
没有实数根,求 的取值范围.
解:
0.
变式3
如果关于 的一元二次方程 ,
有实数根,求 的取值范围.
解:
0.
例2
若关于 的方程 ,
有两个实数根,求正整数 的值.
解:题意,得
.
,
.
+ 4 + 20
+ 24 .
.
, 为正整数,
.
例3
关于的一元二次方程, 若方程有两个相等的实数根,请比较 的大小,并说明理由.
解:题意,得
,
,
例4
已知:关于 的方程 实数根.
求 的取值范围;
若方程的根为有理数,求正整数 的值.
例4
已知:关于 的方程 实数根.
求 的取值范围;
解:时,方程为 ,方程有一个实数根;
时,方程为一元二次方程.
例4
已知:关于 的方程 实数根.
若方程的根为有理数,求正整数 的值.
正整数,
,方程为一元二次方程.
.
分析
例4
已知:关于 的方程 实数根.
若方程的根为有理数,求正整数 的值.
正整数,
, = ;
, = ;
, = ;
, = .
的根为有理数,
为有理数.
或.
或时,方程的根为有理数.
例5
已知关于 的方程 .
求证:方程总有两个不相等的实数根;
若方程的两个实数根都是整数,求整数 的值.
例5
已知关于 的方程 .
求证:方程总有两个不相等的实数根;
证明:
.
例5
已知关于 的方程 .
若方程的两个实数根都是整数,求整数 的值.
解:
,
例5
已知关于 的方程 .
若方程的两个实数根都是整数,求整数 的值.
.
方程的两个实数根都是整数,且 为整数,
解:
例6
如果关于 的一元二次方程 两个相等的实数根,判断以正数 为边长的三角
形的形状.
,
,
,
.
例6
如果关于 的一元二次方程 两个相等的实数根,判断以正数 为边长的三角
形的形状.
.
此一元二次方程两个相等实数根,
.
.
.
.
课
堂
小
结
1
一元二次方程,根的判别式和方程根的情况之间的关系:
方程有两个不相等的实数根;
2
在运用判别式解决问题时先判断方程的类型,根据根的情况,以及字母系数的限定条件,解决相应问题.
课后作业
1
已知关于 的一元二次方程
有两个相等的实数根,求 的值.
2
已知关于 的一元二次方程
有两个不相等的实数根,求 的取值范围.
解一元二次方程——
一元二次方程根的判别式
(第一课时)
复习回顾
解一元二次方程的方法有:
直接开平方法,配方法,公式法,因式分解法.
1
配方法和公式法是解一元二次方程的通法.
2
思考
一元二次方程的根的情况,由哪些因素决定呢?
思考
一元二次方程求根公式的推导过程
.
解:两边同时除以,得
.
移项,得
.
.
配方,得
,
因为,所以 .
当 时, .
方程有实数根.
由于,所以 .
当 时,
.
.
取任何实数都不能使
方程无实数根.
引入新知
一般地,式子叫做一元二次方程根的判别式,通常用希腊字母“”表示它,即 .
归纳
当 时,方程有实数根;
当 时,方程没有实数根.
思考
在存在实数根的情况下,我们还能判断出实数根的什么情况呢?
思考
一元二次方程
当 这时 .
方程有两个不相等实数根.
,
.
.
当 .
,
方程有两个相等实数根.
.
一元二次方程
归纳
一元二次方程 根的情况:
当 时,方程有两个不相等的实数根;
当 时,方程有两个相等的实数根;
当 时,方程没有实数根.
归纳
不求出一元二次方程的根,判断下列方程根的情况:
例1
;
;
;
不求出一元二次方程的根,判断下列方程根的情况:
例1
;
解:
一元二次方程有两个不相等的实数根.
不求出一元二次方程的根,判断下列方程根的情况:
例1
;
解:
.
一元二次方程有两个不相等的实数根.
归纳
不解方程,判断一元二次方程根的情况的一般步骤:
归纳
;
.
不求出一元二次方程的根,判断下列方程根的情况:
例1
;
;
解:
一元二次方程有两个相等实数根.
解:
.
一元二次方程无实数根.
在不解方程的情况下,判断下列关于 的一元二次方程
根的情况.
例2
解:
分析
分析
当
分析
分析
当 时,
当时,
一元二次方程有两个不相等的实数根;
一元二次方程有两个相等的实数根.
当
分析
分析
一元二次方程有两个实数根.
当
分析
分析
一元二次方程有实数根.
当
在不解方程的情况下,判断下列关于 的一元二次方程
根的情况.
例2
解:
所以 有实数根.
在不解方程的情况下,判断下列关于 的方程
根的情况.
例3
解:
,
一元二次方程有两个不相等的实数根.
求证:不论 取何实数,关于 的一元二次方程
有两个不相等的实数根.
例4
证明:
,
一元二次方程有
两个不相等的实数根.
课
堂
小
结
1
一元二次方程根的判别式的定义.
2
一元二次方程根的判别式判别一元二次方程根的情况:
当 时,方程有两个不相等的实数根;
当 时,方程有两个相等的实数根;
当 时,方程没有实数根.
课
堂
小
结
1
一元二次方程根的判别式的定义.
2
一元二次方程根的判别式判别一元二次方程根的情况:
当 时,方程有两个实数根,
或方程有实数根;
当 时,方程没有实数根.
课后作业
1
利用判别式判断下列方程的根的情况.
,
,
.
2
在不解方程的情况下,判断关于 的一元二次方程
的情况.
3
求证:不论 取何实数,关于 的方程
有实数根.
解一元二次方程——
一元二次方程根的判别式
(第二课时)
复习回顾
一元二次方程
.
当 时,方程有两个不相等的实数根;
当 时,方程有两个相等的实数根;
当 时,方程没有实数根.
引入新知
一元二次方程
,
方程有两个不相等的实数根,则;
方程有两个相等的实数根,则;
方程没有实数根,则.
由一元二次方程求根公式的推导过程可知
,
当 时,方程的实数根为
引入新知
一元二次方程
,
方程有两个不相等的实数根,则;
方程有两个相等的实数根,则;
方程没有实数根,则.
例1
如果关于 的一元二次方程 ,
有两个不相等的实数根,求 的取值范围.
解:
.
,
.
.
变式1
如果关于 的一元二次方程 ,
有两个不相等的实数根,求 的取值范围.
变式2
如果关于 的一元二次方程 ,
没有实数根,求 的取值范围.
变式1
如果关于 的一元二次方程 ,
有两个不相等的实数根,求 的取值范围.
解:
0.
变式2
如果关于 的一元二次方程 ,
没有实数根,求 的取值范围.
解:
0.
变式3
如果关于 的一元二次方程 ,
有实数根,求 的取值范围.
解:
0.
例2
若关于 的方程 ,
有两个实数根,求正整数 的值.
解:题意,得
.
,
.
+ 4 + 20
+ 24 .
.
, 为正整数,
.
例3
关于的一元二次方程, 若方程有两个相等的实数根,请比较 的大小,并说明理由.
解:题意,得
,
,
例4
已知:关于 的方程 实数根.
求 的取值范围;
若方程的根为有理数,求正整数 的值.
例4
已知:关于 的方程 实数根.
求 的取值范围;
解:时,方程为 ,方程有一个实数根;
时,方程为一元二次方程.
例4
已知:关于 的方程 实数根.
若方程的根为有理数,求正整数 的值.
正整数,
,方程为一元二次方程.
.
分析
例4
已知:关于 的方程 实数根.
若方程的根为有理数,求正整数 的值.
正整数,
, = ;
, = ;
, = ;
, = .
的根为有理数,
为有理数.
或.
或时,方程的根为有理数.
例5
已知关于 的方程 .
求证:方程总有两个不相等的实数根;
若方程的两个实数根都是整数,求整数 的值.
例5
已知关于 的方程 .
求证:方程总有两个不相等的实数根;
证明:
.
例5
已知关于 的方程 .
若方程的两个实数根都是整数,求整数 的值.
解:
,
例5
已知关于 的方程 .
若方程的两个实数根都是整数,求整数 的值.
.
方程的两个实数根都是整数,且 为整数,
解:
例6
如果关于 的一元二次方程 两个相等的实数根,判断以正数 为边长的三角
形的形状.
,
,
,
.
例6
如果关于 的一元二次方程 两个相等的实数根,判断以正数 为边长的三角
形的形状.
.
此一元二次方程两个相等实数根,
.
.
.
.
课
堂
小
结
1
一元二次方程,根的判别式和方程根的情况之间的关系:
方程有两个不相等的实数根;
2
在运用判别式解决问题时先判断方程的类型,根据根的情况,以及字母系数的限定条件,解决相应问题.
课后作业
1
已知关于 的一元二次方程
有两个相等的实数根,求 的值.
2
已知关于 的一元二次方程
有两个不相等的实数根,求 的取值范围.
同课章节目录
