人教版九年级数学上册24.4弧长和扇形面积 第2课时教学课件(共32张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.4弧长和扇形面积 第2课时教学课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 22:40:06 | ||
图片预览






文档简介
(共32张PPT)
(第二课时)
弧长和扇形面积
复习回顾
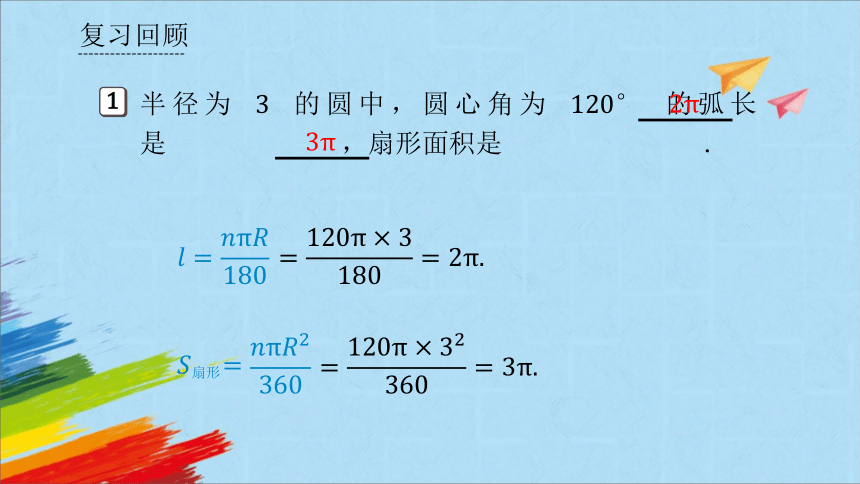
半径为 的圆中,圆心角为 的弧长是 ,扇形面积是 .
1
扇形
复习回顾
半径为 的圆中,扇形面积为 ,则它的弧长
为 .
2
扇形
圆锥
圆锥再认识
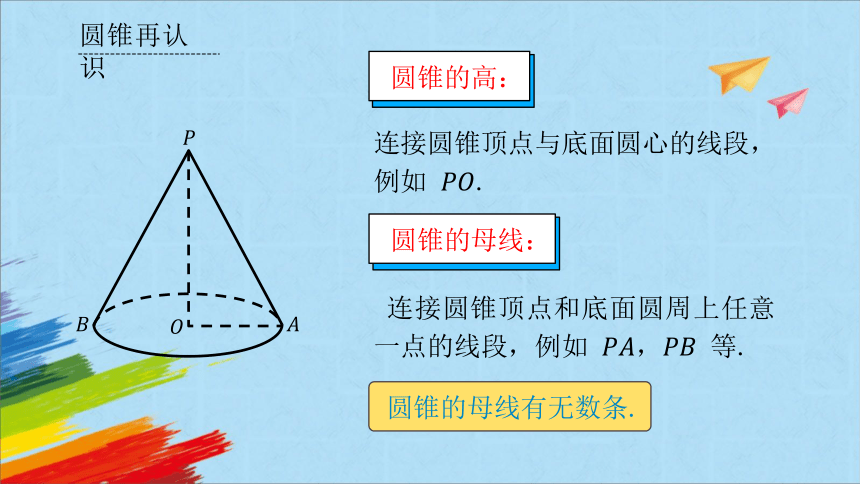
连接圆锥顶点与底面圆心的线段,例如 .
圆锥的高:
连接圆锥顶点和底面圆周上任意一点的线段,例如 , 等.
圆锥的母线:
圆锥的母线有无数条.
圆锥再认识
圆锥的母线、高、底面圆的半径之间的关系:
圆锥的母线长都相等.
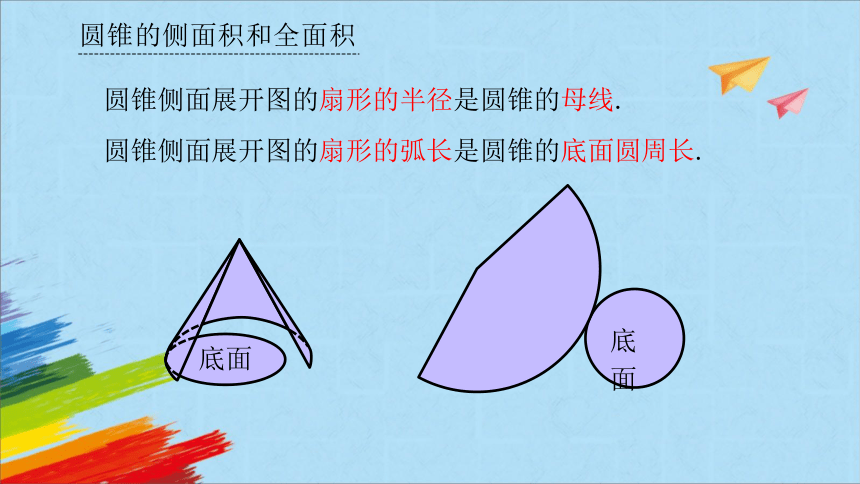
圆锥的侧面积和全面积
底面
底面
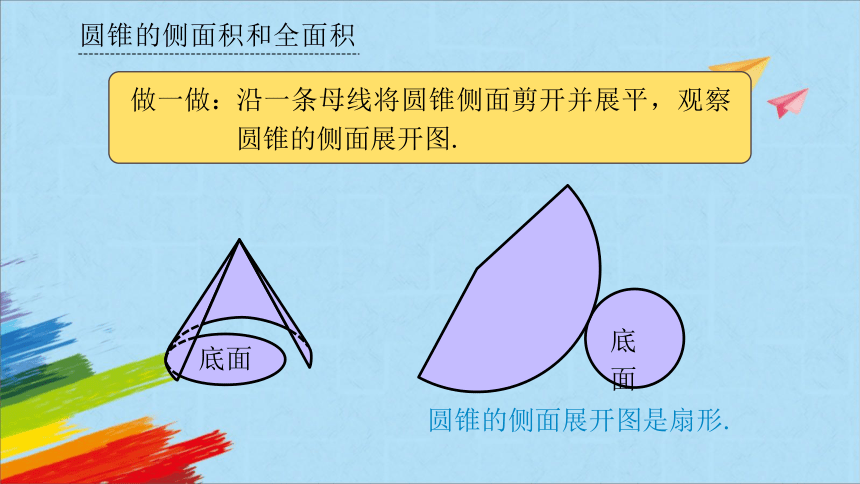
圆锥的侧面展开图是扇形.
做一做:
沿一条母线将圆锥侧面剪开并展平,观察圆锥的侧面展开图.
圆锥的侧面积和全面积
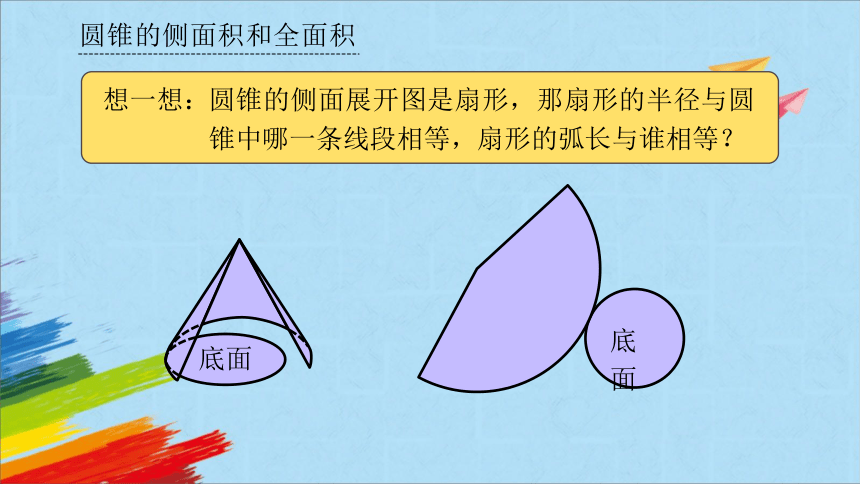
想一想:
圆锥的侧面展开图是扇形,那扇形的半径与圆锥中哪一条线段相等,扇形的弧长与谁相等?
底面
底面
圆锥的侧面积和全面积
圆锥侧面展开图的扇形的半径是圆锥的母线.
圆锥侧面展开图的扇形的弧长是圆锥的底面圆周长.
底面
底面
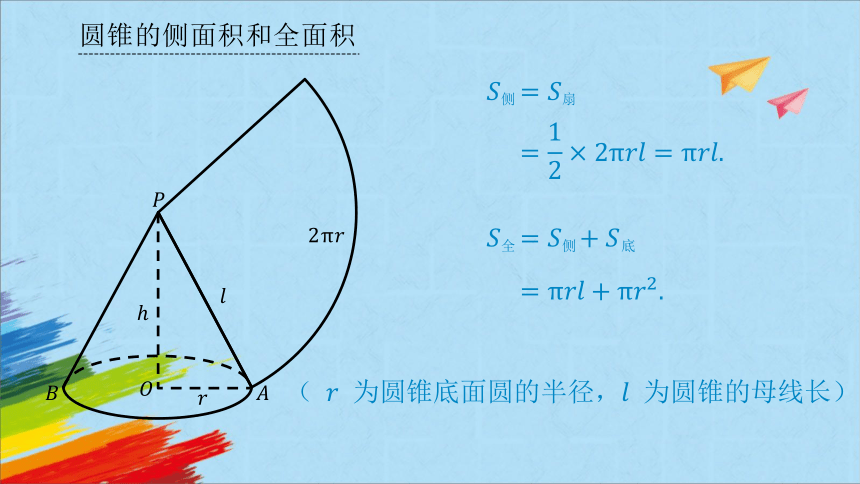
圆锥的侧面积和全面积
( 为圆锥底面圆的半径, 为圆锥的母线长)
侧
扇
全
侧
底
练习
侧
已知圆锥的底面直径为 ,母线长为 ,求它的侧面积.
1
练习
侧
已知圆锥底面圆的半径为 ,高为 ,求这个圆锥的侧面积和全面积.
2
全
侧
底
例题
如图,蒙古包可以近似地看作由圆锥和圆柱组成,现想用毛毡搭建 个底面积为 ,高为 ,外围高为 的蒙古包,求至少需要多少平方米的毛毡(结果保留 )?
例1
侧柱
侧锥
分析
例题
解:
蒙古包底面积为 ,高为 ,外围(圆柱)高 ,
底面半径,
圆锥高.
底面圆的周长为:.
圆柱的侧面积.
底面半径,圆锥高,
圆锥的母线长.
圆锥的侧面积.
需要毛毡:.
例题
圆锥的底面直径是 ,母线长 ,求圆锥的全面积和它的侧面展开图中圆心角的度数.
例2
全
侧
底
分析
圆锥侧面展开图的扇形的弧长是圆锥的底面圆周长.
例题
圆锥的底面直径是 ,母线长 ,求圆锥的全面积和它的侧面展开图中圆心角的度数.
例2
分析
圆锥侧面展开图的扇形的面积是圆锥的侧面积.
例题
解:
全
侧
底
例题
例题
圆锥的全面积为 ,它的侧面展开图中扇形圆心角为 度.
练习
如图,圆锥形的烟囱帽的底面圆的直径是母线长是,制作个这样的烟囱冒至少需要多少平方米的铁皮( 取 )?
1
分析
烟囱帽没有底,只是圆锥的侧面. 先计算一个圆锥的侧面积,再算个圆锥的侧面积.
练习
制作 个这样的烟囱帽至少需要 的铁皮.
侧
解:
练习
一个扇形,半径为 ,圆心角为 度,用它做成一个圆锥的侧面,求这个圆锥的底面半径.
2
分析
圆锥侧面展开图的扇形的弧长是圆锥的底面圆周长.
圆锥侧面展开图的扇形的面积是圆锥的侧面积.
练习
这个圆锥的底面半径为 .
解:
练习
这个圆锥的底面半径为 .
解:
例题
如图,圆锥的底面半径为,母线长为,一只蚂蚁要从底面圆周上一点 出发,沿圆锥侧面爬到过母线的轴截面上另一母线上,问它爬行的最短路线长是多少 ?
过圆锥轴(高)的截面,即△
例3
例题
分析
曲面
平面.
圆锥侧面
扇形.
垂线段最短
.
例题
解:
设圆锥侧面展开图的圆心角为 ,
.
根据垂线段最短,当 时 最短.
.
它爬行的最短路线长是 .
练习
已知圆锥底面半径为,母线长为. 若一甲虫从圆锥底面圆上一点出发,沿着圆锥侧面绕行到母线 的中点 ,它所走的最短路程长是多少 ?
3
练习
分析
曲面
平面.
圆锥侧面
扇形.
两点之间线段最短
.
练习
解:
设圆锥侧面展开图的圆心角为 ,
.
根据两点之间线段最短, 为所求.
.
它所走的最短路程长是 .
课
堂
小
结
本节课重点学习了圆锥的侧面积和全面积公式:
侧
全
侧
底
我们可以通过画示意图的方法把握住圆锥及其展开图之间各元素的对应关系,从而更好的理解圆锥侧面积公式.
课后作业
已知圆锥的底面圆半径 ,高 ,求圆锥的侧面积.
1
用一个半径为 ,圆心角为 的扇形围成一个圆锥,求这个圆锥的底面半径.
2
如图,底面半径为,母线长为 的圆锥,一只小蚂蚁若从点 出发,绕侧面一周又回到点 ,求它爬行的最短路线长.
3
(第二课时)
弧长和扇形面积
复习回顾
半径为 的圆中,圆心角为 的弧长是 ,扇形面积是 .
1
扇形
复习回顾
半径为 的圆中,扇形面积为 ,则它的弧长
为 .
2
扇形
圆锥
圆锥再认识
连接圆锥顶点与底面圆心的线段,例如 .
圆锥的高:
连接圆锥顶点和底面圆周上任意一点的线段,例如 , 等.
圆锥的母线:
圆锥的母线有无数条.
圆锥再认识
圆锥的母线、高、底面圆的半径之间的关系:
圆锥的母线长都相等.
圆锥的侧面积和全面积
底面
底面
圆锥的侧面展开图是扇形.
做一做:
沿一条母线将圆锥侧面剪开并展平,观察圆锥的侧面展开图.
圆锥的侧面积和全面积
想一想:
圆锥的侧面展开图是扇形,那扇形的半径与圆锥中哪一条线段相等,扇形的弧长与谁相等?
底面
底面
圆锥的侧面积和全面积
圆锥侧面展开图的扇形的半径是圆锥的母线.
圆锥侧面展开图的扇形的弧长是圆锥的底面圆周长.
底面
底面
圆锥的侧面积和全面积
( 为圆锥底面圆的半径, 为圆锥的母线长)
侧
扇
全
侧
底
练习
侧
已知圆锥的底面直径为 ,母线长为 ,求它的侧面积.
1
练习
侧
已知圆锥底面圆的半径为 ,高为 ,求这个圆锥的侧面积和全面积.
2
全
侧
底
例题
如图,蒙古包可以近似地看作由圆锥和圆柱组成,现想用毛毡搭建 个底面积为 ,高为 ,外围高为 的蒙古包,求至少需要多少平方米的毛毡(结果保留 )?
例1
侧柱
侧锥
分析
例题
解:
蒙古包底面积为 ,高为 ,外围(圆柱)高 ,
底面半径,
圆锥高.
底面圆的周长为:.
圆柱的侧面积.
底面半径,圆锥高,
圆锥的母线长.
圆锥的侧面积.
需要毛毡:.
例题
圆锥的底面直径是 ,母线长 ,求圆锥的全面积和它的侧面展开图中圆心角的度数.
例2
全
侧
底
分析
圆锥侧面展开图的扇形的弧长是圆锥的底面圆周长.
例题
圆锥的底面直径是 ,母线长 ,求圆锥的全面积和它的侧面展开图中圆心角的度数.
例2
分析
圆锥侧面展开图的扇形的面积是圆锥的侧面积.
例题
解:
全
侧
底
例题
例题
圆锥的全面积为 ,它的侧面展开图中扇形圆心角为 度.
练习
如图,圆锥形的烟囱帽的底面圆的直径是母线长是,制作个这样的烟囱冒至少需要多少平方米的铁皮( 取 )?
1
分析
烟囱帽没有底,只是圆锥的侧面. 先计算一个圆锥的侧面积,再算个圆锥的侧面积.
练习
制作 个这样的烟囱帽至少需要 的铁皮.
侧
解:
练习
一个扇形,半径为 ,圆心角为 度,用它做成一个圆锥的侧面,求这个圆锥的底面半径.
2
分析
圆锥侧面展开图的扇形的弧长是圆锥的底面圆周长.
圆锥侧面展开图的扇形的面积是圆锥的侧面积.
练习
这个圆锥的底面半径为 .
解:
练习
这个圆锥的底面半径为 .
解:
例题
如图,圆锥的底面半径为,母线长为,一只蚂蚁要从底面圆周上一点 出发,沿圆锥侧面爬到过母线的轴截面上另一母线上,问它爬行的最短路线长是多少 ?
过圆锥轴(高)的截面,即△
例3
例题
分析
曲面
平面.
圆锥侧面
扇形.
垂线段最短
.
例题
解:
设圆锥侧面展开图的圆心角为 ,
.
根据垂线段最短,当 时 最短.
.
它爬行的最短路线长是 .
练习
已知圆锥底面半径为,母线长为. 若一甲虫从圆锥底面圆上一点出发,沿着圆锥侧面绕行到母线 的中点 ,它所走的最短路程长是多少 ?
3
练习
分析
曲面
平面.
圆锥侧面
扇形.
两点之间线段最短
.
练习
解:
设圆锥侧面展开图的圆心角为 ,
.
根据两点之间线段最短, 为所求.
.
它所走的最短路程长是 .
课
堂
小
结
本节课重点学习了圆锥的侧面积和全面积公式:
侧
全
侧
底
我们可以通过画示意图的方法把握住圆锥及其展开图之间各元素的对应关系,从而更好的理解圆锥侧面积公式.
课后作业
已知圆锥的底面圆半径 ,高 ,求圆锥的侧面积.
1
用一个半径为 ,圆心角为 的扇形围成一个圆锥,求这个圆锥的底面半径.
2
如图,底面半径为,母线长为 的圆锥,一只小蚂蚁若从点 出发,绕侧面一周又回到点 ,求它爬行的最短路线长.
3
同课章节目录
