人教版九年级数学上册21.3实际问题与一元二次方程 教学课件(共124张PPT)
文档属性
| 名称 | 人教版九年级数学上册21.3实际问题与一元二次方程 教学课件(共124张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 22:48:10 | ||
图片预览



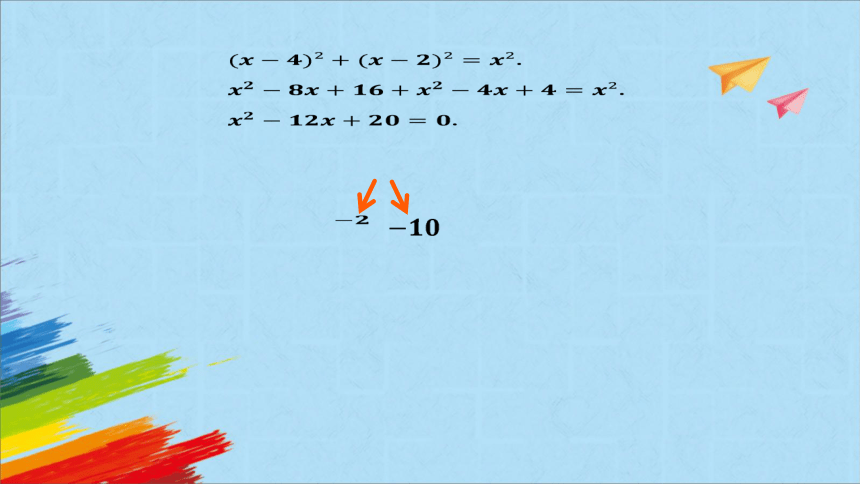
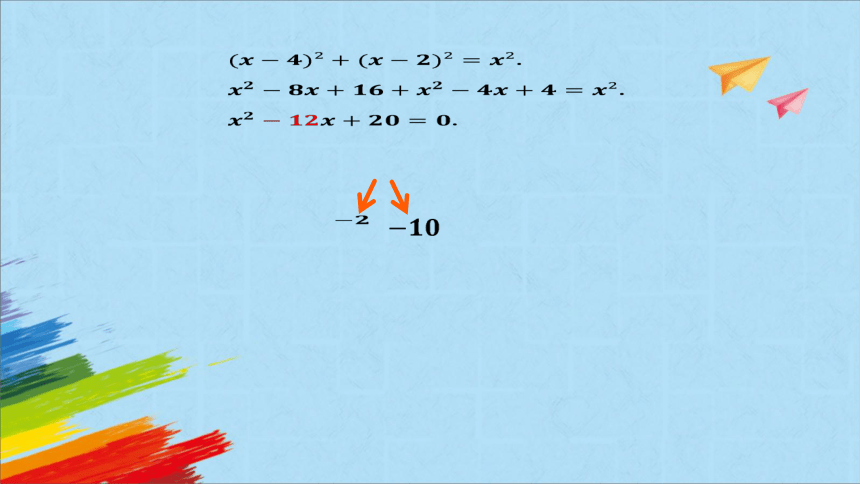
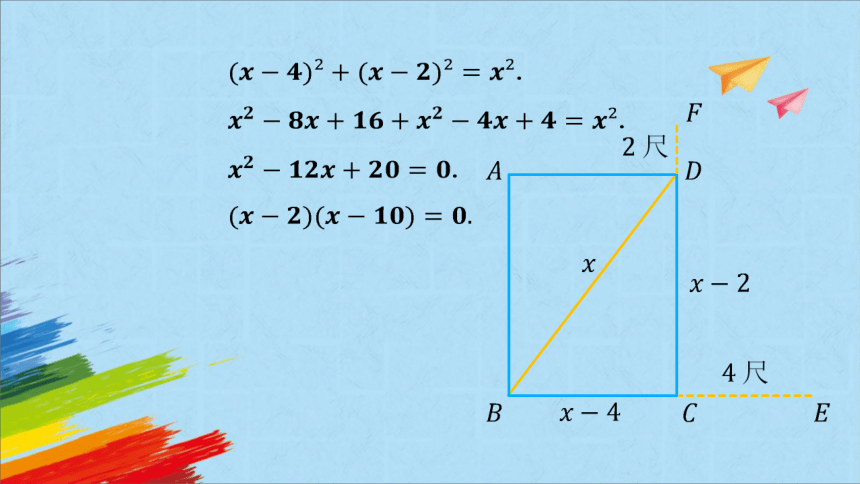



文档简介
(共124张PPT)
实际问题与一元二次方程
(第一课时)
引例
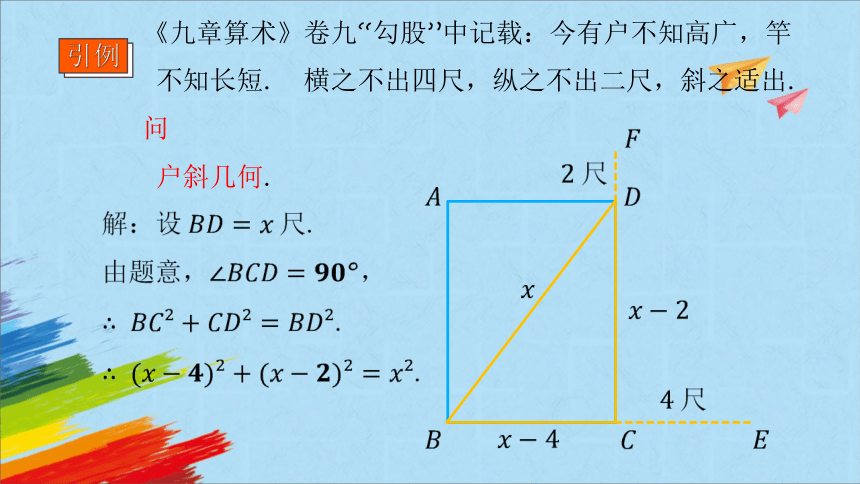
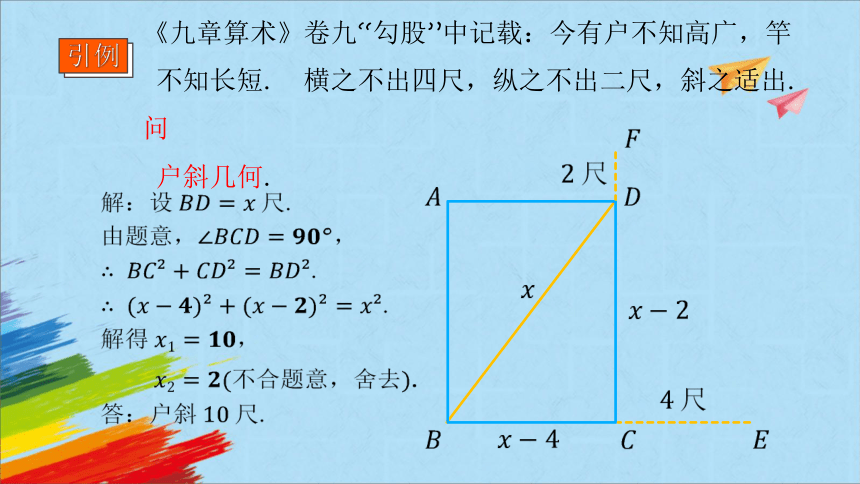
《九章算术》卷九“勾股”中记载:今有户不知高广,竿
不知长短. 横之不出四尺,纵之不出二尺,斜之适出. 问
户斜几何.
注释:横放,竿比门宽长出四尺;竖放,竿比门高出二尺;斜放恰好能出去. 求户斜多长.
引例
《九章算术》卷九“勾股”中记载:今有户不知高广,竿
不知长短. 横之不出四尺,纵之不出二尺,斜之适出. 问
户斜几何.
解:设尺.
由题意,,
.
.
引例
《九章算术》卷九“勾股”中记载:今有户不知高广,竿
不知长短. 横之不出四尺,纵之不出二尺,斜之适出. 问
户斜几何.
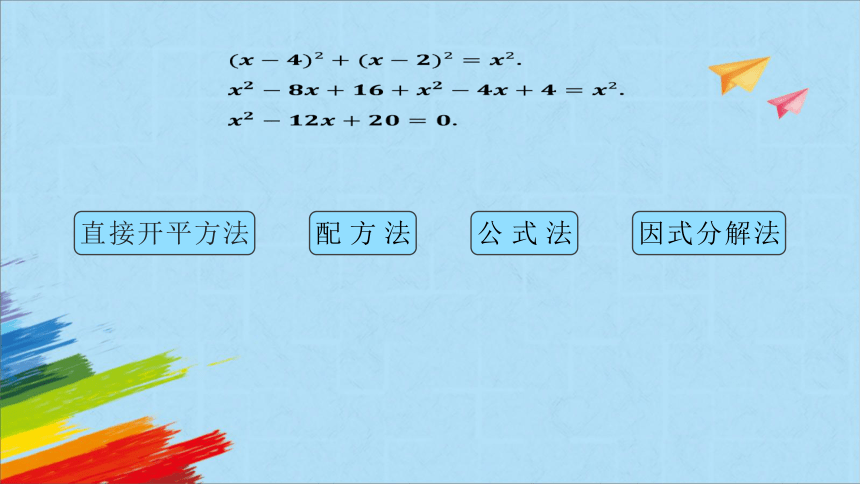
.
.
.
因式分解法
公式法
配方法
直接开平方法
.
.
.
.
.
.
.
.
.
.
.
.
不合题意,舍去.
解:设尺.
由题意,,
.
.
解得,
不合题意,舍去.
答:户斜尺.
引例
《九章算术》卷九“勾股”中记载:今有户不知高广,竿
不知长短. 横之不出四尺,纵之不出二尺,斜之适出. 问
户斜几何.
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
第一轮的传染源有几人?
第一轮的传染源只有个人.
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
如何理解“两轮传染”?
第一轮由个人传染给几个人,为了便于理解,我们先假定为个人,那么第一轮传染后共有个人患流感.
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
第一轮由个人传染给几个人,为了便于理解,我们先假定为个人,那么第一轮传染后共有个人患流感. 这个人就成为第二轮的传染源,每个人又分别传染给 个人,那么第二轮的新患流感人数就为人.
如何理解“两轮传染”?
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
如何理解“共有”?
按照我们刚才的假设,第一轮传染后有名患者,第二轮传染后有名新患者. 那么两轮之后的总人数就是人.
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
如何用算术的方法解决这样的问题?
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
如果用方程的方法,你认为相等关系是什么?
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
设每轮传染中平均每一个人传染了个人.
则第一轮后共有________个人患了流感;
第二轮共有_________个人新患了流感.
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
解:设每轮传染中平均一个人传染了个人.
.
.
.
.
.
.
.
.
.
.
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
解:设每轮传染中平均一个人传染了个人.
.
解得 ,
答:每轮传染中平均一个人传染了个人.
进一步思考:按照这样的情形,三轮之后共有多少人感染流感?
两轮传染之后共有个人患了流感,第三的轮传染源也正是这人,所以第三轮感染的人数是:
.
三轮后感染的总人数是:.
进一步思考:按照这样的情形,三轮之后共有多少人感染流感?
第一轮后:.
第二轮后:.
第三轮后:.
进一步思考:按照这样的情形,轮之后共有多少人感染流感?
第一轮后:.
第二轮后:.
第三轮后:.
……
第轮后.
进一步思考:按照这样的情形,轮之后共有多少人感染流感?
第一轮后:.
第二轮后:.
进一步思考:如果最初有两个人患了流感,按照上述的传染模式,第一轮、第二轮传染之后分别共有多少人感染流感?
第一轮后:.
第二轮后:.
进一步思考:如果最初有两个人患了流感,按照上述的传染模式,第一轮、第二轮传染之后分别共有多少人感染流感?
如果最初有一个人患了流感:
第一轮后有人,第二轮后有,第三轮后有.
如果最初有两个人患了流感:
第一轮后有人,第二轮后有.
如果最初有一个人患了流感:
第一轮后有人,第二轮后有,第三轮后有.
如果最初有两个人患了流感:
第一轮后有人,第二轮后有.
如果最初有一个人患了流感:
第一轮后有人,第二轮后有,第三轮后有.
如果最初有两个人患了流感:
第一轮后有人,第二轮后有.
轮传染后共有人感染流感.
进一步思考:如果最初有个人患了流感,按照上述的传染模式,轮传染之后共有多少人感染流感?
轮后共有人感染流感.
进一步思考:如果最初有个人患了流感,每轮传染中平均一个人传染给个人,那么轮传染之后共有多少人感染流感?
1
练习1
某种植物的主干长出若干数目的支干,每个支干又长出同样数量的小分支,主干、支干和小分支的总数是,每个枝干长出多少个小分支?
主干、支干和小分支的总数:
主干、支干和小分支的总数:
1
练习1
解设每个支干长出个小分支.
.
某种植物的主干长出若干数目的支干,每个支干又长出同样数量的小分支,主干、支干和小分支的总数是,每个枝干长出多少个小分支?
.
.
.
不合题意,舍去,.
1
练习1
解设每个支干长出个小分支.
.
解得不合题意,舍去,.
答:每个支干长出个小分支.
某种植物的主干长出若干数目的支干,每个支干又长出同样数量的小分支,主干、支干和小分支的总数是,每个枝干长出多少个小分支?
1
练习1
进一步思考:这道题和探究有什么区别?
某种植物的主干长出若干数目的支干,每个支干又长出同样数量的小分支,主干、支干和小分支的总数是,每个枝干长出多少个小分支?
进一步思考:这道题和探究有什么区别?
探究中,第一轮的传染源是个人,传染了个人,使得第二轮的传染源变成个人;而练习的题目告诉我们,第一轮是一个主干长出个支干,第二轮只有这个支干(而不包括主干)分别又长出了个小分支.
进一步思考:利用图形说明如何修改练习使之与探究模型相同.
参加足球联赛的每两队之间都进行两场比赛,共要比赛 场. 共有多少个队参加比赛?
解设共有个队参加比赛.
共比赛_________场.
1
练习2
参加足球联赛的每两队之间都进行两场比赛,共要比赛 场. 共有多少个队参加比赛?
解设共有个队参加比赛.
共比赛_________场.
1
练习2
参加足球联赛的每两队之间都进行两场比赛,共要比赛 场. 共有多少个队参加比赛?
解设共有个队参加比赛.
共比赛_________场.
1
练习2
1
练习2
参加足球联赛的每两队之间都进行两场比赛,共要比赛 场. 共有多少个队参加比赛?
解设共有个队参加比赛.
.
.
.
.
解得不合题意,舍去,.
1
练习2
参加足球联赛的每两队之间都进行两场比赛,共要比赛 场. 共有多少个队参加比赛?
解设共有个队参加比赛.
.
解得不合题意,舍去,.
答:共有个队参加比赛.
引例
《九章算术》卷九“勾股”中记载:今有户不知高广,竿
不知长短. 横之不出四尺,纵之不出二尺,斜之适出. 问
户斜几何.
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
1
练习2
参加足球联赛的每两队之间都进行两场比赛,共要比赛 场. 共有多少个队参加比赛?
1
2
3
准确地用含未知数的代数式表达未知量要建立在充分理解题意的基础上;
快速地解一元二次方程的前提是熟练掌握四种方法以及细致地观察;
要结合题目背景对一元二次方程的两个解进行检验和取舍.
课
堂
小
结
4
一元二次方程是刻画现实世界中某些数量关系的有效数学模型.
课
堂
小
结
4
一元二次方程是刻画现实世界中某些数量关系的有效数学模型. 在运用一元二次方程分析、表达和解决实际问题的过程中,要注意体会建立数学模型解决实际问题的思想和方法.
课
堂
小
结
再 见
利用方程解决实际问题的基本过程
实际问题
方程
方程的解
实际问题的答案
数学模型
探究
年,研究人员在某杂志发表论文说,他们分析了两颗卫星的观测数据,发现在年至年间全球绿化面积增加了.
探究
年,研究人员在某杂志发表论文说,他们分析了两颗卫星的观测数据,发现在年至年间全球绿化面积增加了. 其中约四分之一来自中国,贡献比例居全球首位. 研究人员认为原因是中国在植树造林和集约农业等方面有突出表现.
探究
年,研究人员在某杂志发表论文说,他们分析了两颗卫星的观测数据,发现在年至年间全
球绿化面积增加了. 其中约四分之一来自中国,贡献比例居全球首位. 研究人员认为原因是中国在植树造林和集约农业等方面有突出表现.
经调查,年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
探究
年,研究人员在某杂志发表论文说,他们分析了两颗卫星的观测数据,发现在年至年间全球绿化面积增加了. 其中约四分之一来自中国,贡献比例居全球首位. 研究人员认为原因是中国在植树造林和集约农业等方面有突出表现.
经调查,年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
探究
年,研究人员在某杂志发表论文说,他们分析了两颗卫星的观测数据,发现在年至年间全球绿化面积增加了. 其中约四分之一来自中国,贡献比例居全球首位. 研究人员认为原因是中国在植树造林和集约农业等方面有突出表现.
经调查,年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
探究
年,研究人员在某杂志发表论文说,他们分析了两颗卫星的观测数据,发现在年至年间全球绿化面积增加了. 其中约四分之一来自中国,贡献比例居全球首位. 研究人员认为原因是中国在植树造林和集约农业等方面有突出表现.
经调查,年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
探究
年
在年至年间全球绿化面积增加了. 年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
探究
年
在年至年间全球绿化面积增加了. 年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
增长率
探究
在年至年间全球绿化面积增加了. 年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
年
探究
在年至年间全球绿化面积增加了. 年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
年
探究
如果年,全球绿化面积能达到多少呢?
变化前
变化后
变化前数量变化后数量
年
探究
年
如果年,全球绿化面积能达到多少呢?
变化前数量变化后数量
探究
年
如果年,全球绿化面积能达到多少呢?
变化前数量变化后数量
变化前
变化后
探究
年
变化前
变化后
如果年,全球绿化面积能达到多少呢?
变化前数量变化后数量
探究
年
变化前
变化后
如果年,全球绿化面积能达到多少呢?
变化前数量变化后数量
探究
如果年的全球绿化面积又该怎么表示呢?
年
年
探究
如果年的全球绿化面积又该怎么表示呢?
年
年
探究
如果年的全球绿化面积又该怎么表示呢?
年
年
探究
如果年的全球绿化面积又该怎么表示呢?
年
年
年全球绿化面积大约是多少亿公顷?
亿公顷.
如果保持这个增长率,那么到年,全球绿化面积预计有多少亿公顷?
亿公顷.
探究
经调查,年全球绿化面积大约是亿公顷,在
年全球绿化面积增加了
探究
增长率用表示,则年全球绿化面积表示为:
.
当增长率为多少时,年的全球绿化面积可以达到亿
公顷?(精确到)
.
经调查,年全球绿化面积大约是亿公顷,在
年全球绿化面积增加了
利用方程解决实际问题的基本过程
当增长率为多少时,年的全球绿化面积可以达到亿公顷?(精确到)
解:设增长率为.
.
.
实际问题转化为
一元二次方程
解:设增长率为.
.
,得
(不合题意,舍去)
答:增长率约为.
求解一元二次方程
得到实际问题答案
实际问题转化为
一元二次方程
利用方程解决实际问题的基本过程
当增长率为多少时,年的全球绿化面积可以达到亿公顷?(精确到)
探究
类似地,这种变化率的问题在实际生活中有许多原型,例如经济增长率、人口增长率等.
探究
类似地,这种变化率的问题在实际生活中有许多原型,例如经济增长率、人口增长率等. 本节讨论的是两轮即两个时间段的平均变化率,它可以用一元二次方程作为数学模型,设平均变化率为,则可以得到这样的关系:
变化前的数量变化后的数量
增长率
增长后
增长后
增长后
若连续两轮增长
增长率
下降率
下降后
下降率
下降后
下降后
若连续两轮下降
下降后
若连续两轮变化时:
增长后
变化前数量 后数量
1
练习1
某区为发展教育事业,加强了对教育经费的投入,年投入了万元,年计划投入万元. 设教育经费的年平均增长率为,根据题意,下面所列方程正确的是( ).
1
练习1
某区为发展教育事业,加强了对教育经费的投入,年投入了万元,年计划投入万元. 设教育经费的年平均增长率为,根据题意,下面所列方程正确的是( ).
1
练习1
某区为发展教育事业,加强了对教育经费的投入,年投入了万元,年计划投入万元. 设教育经费的年平均增长率为,根据题意,下面所列方程正确的是( ).
某区为发展教育事业,加强了对教育经费的投入,年投入了万元,年计划投入万元. 设教育经费的年平均增长率为,根据题意,下面所列方程正确的是( ).
1
练习1
1
练习2
某商品原价是元,经连续两次降价后售价为元,设平均每次降价的百分率为,则下面所列方程正确的是( ).
变化前数量 后数量
1
练习2
某商品原价是元,经连续两次降价后售价为元,设平均每次降价的百分率为,则下面所列方程正确的是( ).
变化前数量 后数量
1
练习2
某商品原价是元,经连续两次降价后售价为元,设平均每次降价的百分率为,则下面所列方程正确的是( ).
变化前数量 后数量
某商品原价是元,经连续两次降价后售价为元,设平均每次降价的百分率为,则下面所列方程正确的是( ).
1
练习2
变化前数量 后数量
某商品原价是元,经连续两次降价后售价为元,设平均每次降价的百分率为,则下面所列方程正确的是( ).
1
练习2
变化前数量 后数量
1
例题
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
两种药品成本的年平均下降额各是多少?
1
例题
两种药品成本的年平均下降额各是多少?
成本的年平均下降率
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
甲种药品
1
例题
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
甲种药品
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
甲种药品
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
甲种药品
乙种药品
1
例题
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
甲种药品
乙种药品
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
甲种药品
乙种药品
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
甲种药品
乙种药品
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两年前 现在 平均下降额
甲种药品
乙种药品
答:甲乙药品年平均下降额分别为元、元.
两种药品成本的年平均下降额各是多少?
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
两种药品成本的年平均下降额各是多少?
答:甲乙药品年平均下降额分别为元、元.
两种药品成本的年平均下降率各是多少?哪个大?
1
例题
两种药品成本的年平均下降额各是多少?
答:甲乙药品年平均下降额分别为元、元.
两种药品成本的年平均下降率各是多少?哪个大?
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
两种药品成本的年平均下降率各是多少?哪个大?
变化前数量 后数量
1
例题
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
甲:设甲种药品成本的年平均下降率为.
则.
1
例题
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
两种药品成本的年平均下降率各是多少?哪个大?
分析
.
:整理,得
.
即 .
直接开平方,得
.
.
:整理,得
.
即 .
直接开平方,得
.
.
两种药品成本的年平均下降率各是多少?哪个大?
1
例题
甲:设甲种药品成本的年平均下降率为.
则.
解方程,得.
分析
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
甲:设甲种药品成本的年平均下降率为.
则.
解方程,得舍去.
即甲种药品成本的年平均下降率约为.
分析
两种药品成本的年平均下降率各是多少?哪个大?
1
例题
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
两种药品成本的年平均下降率各是多少?哪个大?
乙:设乙种药品成本的年平均下降率为.
则.
解方程,得舍去.
即乙种药品成本的年平均下降率约为,一样大.
分析
1
例题
两种药品成本的年平均下降率各是多少?哪个大?
乙:设乙种药品成本的年平均下降率为.
则.
解方程,得舍去.
即乙种药品成本的年平均下降率约为,一样大.
分析
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两种药品成本的年平均下降率各是多少?哪个大?
乙:设乙种药品成本的年平均下降率为.
则.
解方程,得舍去.
即乙种药品成本的年平均下降率约为,一样大.
分析
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
思考
1
2
3
经过计算,你可以得到什么结论?
成本下降额大的药品,它的成本下降率一定也大吗?
应怎样全面的比较几个对象的变化状况?
思考
1
两种药品成本的年平均下降额不同,甲为元,乙为元.
但它们的年平均下降率相同,约为.
经过计算,你可以得到什么结论?
思考
2
不一定.
乙的年平均下降额大,但年平均率和甲相同.
成本下降额大的药品,它的成本下降率一定也大吗?
思考
3
成本下降额表示绝对变化量,成本下降率表示相对变化量,两者兼顾才能全面比较对象的变化状况.
应怎样全面的比较几个对象的变化状况?
变化前数量变化后数量.
转化数学问题
阅读分析题意,建立模型,列出方程.
课
堂
小
结
转化数学问题
阅读分析题意,建立模型,列出方程.
求解数学问题
选择合适的方法求解数学问题.
解决实际问题
经过检验,找到符合题意的答案解决实际问题.
课
堂
小
结
一元二次方程是刻画现实世界中某些数量关系的有效数学模型.
课
堂
小
结
一元二次方程是刻画现实世界中某些数量关系的有效数学模型. 在运用一元二次方程分析、表达和解决实际问题的过程中,要注意体会建立数学模型解决实际问题的思想和方法.
课
堂
小
结
实际问题
一元二次方程
一元二次方程的解
实际问题的答案
数学模型
课
堂
小
结
青山村种的水稻年平均每公顷产,年平均
每公顷产,求水稻每公顷产量的年平均增长率.
某银行经过最近两次降息,使一年期存款的年利率由降
至,平均每次降息的百分率是多少结果写出的形
式,其中保留小数点后两位).
课后作业
实际问题与一元二次方程
(第一课时)
引例
《九章算术》卷九“勾股”中记载:今有户不知高广,竿
不知长短. 横之不出四尺,纵之不出二尺,斜之适出. 问
户斜几何.
注释:横放,竿比门宽长出四尺;竖放,竿比门高出二尺;斜放恰好能出去. 求户斜多长.
引例
《九章算术》卷九“勾股”中记载:今有户不知高广,竿
不知长短. 横之不出四尺,纵之不出二尺,斜之适出. 问
户斜几何.
解:设尺.
由题意,,
.
.
引例
《九章算术》卷九“勾股”中记载:今有户不知高广,竿
不知长短. 横之不出四尺,纵之不出二尺,斜之适出. 问
户斜几何.
.
.
.
因式分解法
公式法
配方法
直接开平方法
.
.
.
.
.
.
.
.
.
.
.
.
不合题意,舍去.
解:设尺.
由题意,,
.
.
解得,
不合题意,舍去.
答:户斜尺.
引例
《九章算术》卷九“勾股”中记载:今有户不知高广,竿
不知长短. 横之不出四尺,纵之不出二尺,斜之适出. 问
户斜几何.
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
第一轮的传染源有几人?
第一轮的传染源只有个人.
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
如何理解“两轮传染”?
第一轮由个人传染给几个人,为了便于理解,我们先假定为个人,那么第一轮传染后共有个人患流感.
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
第一轮由个人传染给几个人,为了便于理解,我们先假定为个人,那么第一轮传染后共有个人患流感. 这个人就成为第二轮的传染源,每个人又分别传染给 个人,那么第二轮的新患流感人数就为人.
如何理解“两轮传染”?
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
如何理解“共有”?
按照我们刚才的假设,第一轮传染后有名患者,第二轮传染后有名新患者. 那么两轮之后的总人数就是人.
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
如何用算术的方法解决这样的问题?
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
如果用方程的方法,你认为相等关系是什么?
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
设每轮传染中平均每一个人传染了个人.
则第一轮后共有________个人患了流感;
第二轮共有_________个人新患了流感.
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
解:设每轮传染中平均一个人传染了个人.
.
.
.
.
.
.
.
.
.
.
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
解:设每轮传染中平均一个人传染了个人.
.
解得 ,
答:每轮传染中平均一个人传染了个人.
进一步思考:按照这样的情形,三轮之后共有多少人感染流感?
两轮传染之后共有个人患了流感,第三的轮传染源也正是这人,所以第三轮感染的人数是:
.
三轮后感染的总人数是:.
进一步思考:按照这样的情形,三轮之后共有多少人感染流感?
第一轮后:.
第二轮后:.
第三轮后:.
进一步思考:按照这样的情形,轮之后共有多少人感染流感?
第一轮后:.
第二轮后:.
第三轮后:.
……
第轮后.
进一步思考:按照这样的情形,轮之后共有多少人感染流感?
第一轮后:.
第二轮后:.
进一步思考:如果最初有两个人患了流感,按照上述的传染模式,第一轮、第二轮传染之后分别共有多少人感染流感?
第一轮后:.
第二轮后:.
进一步思考:如果最初有两个人患了流感,按照上述的传染模式,第一轮、第二轮传染之后分别共有多少人感染流感?
如果最初有一个人患了流感:
第一轮后有人,第二轮后有,第三轮后有.
如果最初有两个人患了流感:
第一轮后有人,第二轮后有.
如果最初有一个人患了流感:
第一轮后有人,第二轮后有,第三轮后有.
如果最初有两个人患了流感:
第一轮后有人,第二轮后有.
如果最初有一个人患了流感:
第一轮后有人,第二轮后有,第三轮后有.
如果最初有两个人患了流感:
第一轮后有人,第二轮后有.
轮传染后共有人感染流感.
进一步思考:如果最初有个人患了流感,按照上述的传染模式,轮传染之后共有多少人感染流感?
轮后共有人感染流感.
进一步思考:如果最初有个人患了流感,每轮传染中平均一个人传染给个人,那么轮传染之后共有多少人感染流感?
1
练习1
某种植物的主干长出若干数目的支干,每个支干又长出同样数量的小分支,主干、支干和小分支的总数是,每个枝干长出多少个小分支?
主干、支干和小分支的总数:
主干、支干和小分支的总数:
1
练习1
解设每个支干长出个小分支.
.
某种植物的主干长出若干数目的支干,每个支干又长出同样数量的小分支,主干、支干和小分支的总数是,每个枝干长出多少个小分支?
.
.
.
不合题意,舍去,.
1
练习1
解设每个支干长出个小分支.
.
解得不合题意,舍去,.
答:每个支干长出个小分支.
某种植物的主干长出若干数目的支干,每个支干又长出同样数量的小分支,主干、支干和小分支的总数是,每个枝干长出多少个小分支?
1
练习1
进一步思考:这道题和探究有什么区别?
某种植物的主干长出若干数目的支干,每个支干又长出同样数量的小分支,主干、支干和小分支的总数是,每个枝干长出多少个小分支?
进一步思考:这道题和探究有什么区别?
探究中,第一轮的传染源是个人,传染了个人,使得第二轮的传染源变成个人;而练习的题目告诉我们,第一轮是一个主干长出个支干,第二轮只有这个支干(而不包括主干)分别又长出了个小分支.
进一步思考:利用图形说明如何修改练习使之与探究模型相同.
参加足球联赛的每两队之间都进行两场比赛,共要比赛 场. 共有多少个队参加比赛?
解设共有个队参加比赛.
共比赛_________场.
1
练习2
参加足球联赛的每两队之间都进行两场比赛,共要比赛 场. 共有多少个队参加比赛?
解设共有个队参加比赛.
共比赛_________场.
1
练习2
参加足球联赛的每两队之间都进行两场比赛,共要比赛 场. 共有多少个队参加比赛?
解设共有个队参加比赛.
共比赛_________场.
1
练习2
1
练习2
参加足球联赛的每两队之间都进行两场比赛,共要比赛 场. 共有多少个队参加比赛?
解设共有个队参加比赛.
.
.
.
.
解得不合题意,舍去,.
1
练习2
参加足球联赛的每两队之间都进行两场比赛,共要比赛 场. 共有多少个队参加比赛?
解设共有个队参加比赛.
.
解得不合题意,舍去,.
答:共有个队参加比赛.
引例
《九章算术》卷九“勾股”中记载:今有户不知高广,竿
不知长短. 横之不出四尺,纵之不出二尺,斜之适出. 问
户斜几何.
1
探究1
有一个人患了流感,经过两轮传染后,共有个人患了流感,每轮传染中平均一个人传染了几个人?
1
练习2
参加足球联赛的每两队之间都进行两场比赛,共要比赛 场. 共有多少个队参加比赛?
1
2
3
准确地用含未知数的代数式表达未知量要建立在充分理解题意的基础上;
快速地解一元二次方程的前提是熟练掌握四种方法以及细致地观察;
要结合题目背景对一元二次方程的两个解进行检验和取舍.
课
堂
小
结
4
一元二次方程是刻画现实世界中某些数量关系的有效数学模型.
课
堂
小
结
4
一元二次方程是刻画现实世界中某些数量关系的有效数学模型. 在运用一元二次方程分析、表达和解决实际问题的过程中,要注意体会建立数学模型解决实际问题的思想和方法.
课
堂
小
结
再 见
利用方程解决实际问题的基本过程
实际问题
方程
方程的解
实际问题的答案
数学模型
探究
年,研究人员在某杂志发表论文说,他们分析了两颗卫星的观测数据,发现在年至年间全球绿化面积增加了.
探究
年,研究人员在某杂志发表论文说,他们分析了两颗卫星的观测数据,发现在年至年间全球绿化面积增加了. 其中约四分之一来自中国,贡献比例居全球首位. 研究人员认为原因是中国在植树造林和集约农业等方面有突出表现.
探究
年,研究人员在某杂志发表论文说,他们分析了两颗卫星的观测数据,发现在年至年间全
球绿化面积增加了. 其中约四分之一来自中国,贡献比例居全球首位. 研究人员认为原因是中国在植树造林和集约农业等方面有突出表现.
经调查,年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
探究
年,研究人员在某杂志发表论文说,他们分析了两颗卫星的观测数据,发现在年至年间全球绿化面积增加了. 其中约四分之一来自中国,贡献比例居全球首位. 研究人员认为原因是中国在植树造林和集约农业等方面有突出表现.
经调查,年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
探究
年,研究人员在某杂志发表论文说,他们分析了两颗卫星的观测数据,发现在年至年间全球绿化面积增加了. 其中约四分之一来自中国,贡献比例居全球首位. 研究人员认为原因是中国在植树造林和集约农业等方面有突出表现.
经调查,年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
探究
年,研究人员在某杂志发表论文说,他们分析了两颗卫星的观测数据,发现在年至年间全球绿化面积增加了. 其中约四分之一来自中国,贡献比例居全球首位. 研究人员认为原因是中国在植树造林和集约农业等方面有突出表现.
经调查,年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
探究
年
在年至年间全球绿化面积增加了. 年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
探究
年
在年至年间全球绿化面积增加了. 年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
增长率
探究
在年至年间全球绿化面积增加了. 年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
年
探究
在年至年间全球绿化面积增加了. 年全球绿化面积大约是亿公顷,则年全球绿化面积大约是多少亿公顷?
年
探究
如果年,全球绿化面积能达到多少呢?
变化前
变化后
变化前数量变化后数量
年
探究
年
如果年,全球绿化面积能达到多少呢?
变化前数量变化后数量
探究
年
如果年,全球绿化面积能达到多少呢?
变化前数量变化后数量
变化前
变化后
探究
年
变化前
变化后
如果年,全球绿化面积能达到多少呢?
变化前数量变化后数量
探究
年
变化前
变化后
如果年,全球绿化面积能达到多少呢?
变化前数量变化后数量
探究
如果年的全球绿化面积又该怎么表示呢?
年
年
探究
如果年的全球绿化面积又该怎么表示呢?
年
年
探究
如果年的全球绿化面积又该怎么表示呢?
年
年
探究
如果年的全球绿化面积又该怎么表示呢?
年
年
年全球绿化面积大约是多少亿公顷?
亿公顷.
如果保持这个增长率,那么到年,全球绿化面积预计有多少亿公顷?
亿公顷.
探究
经调查,年全球绿化面积大约是亿公顷,在
年全球绿化面积增加了
探究
增长率用表示,则年全球绿化面积表示为:
.
当增长率为多少时,年的全球绿化面积可以达到亿
公顷?(精确到)
.
经调查,年全球绿化面积大约是亿公顷,在
年全球绿化面积增加了
利用方程解决实际问题的基本过程
当增长率为多少时,年的全球绿化面积可以达到亿公顷?(精确到)
解:设增长率为.
.
.
实际问题转化为
一元二次方程
解:设增长率为.
.
,得
(不合题意,舍去)
答:增长率约为.
求解一元二次方程
得到实际问题答案
实际问题转化为
一元二次方程
利用方程解决实际问题的基本过程
当增长率为多少时,年的全球绿化面积可以达到亿公顷?(精确到)
探究
类似地,这种变化率的问题在实际生活中有许多原型,例如经济增长率、人口增长率等.
探究
类似地,这种变化率的问题在实际生活中有许多原型,例如经济增长率、人口增长率等. 本节讨论的是两轮即两个时间段的平均变化率,它可以用一元二次方程作为数学模型,设平均变化率为,则可以得到这样的关系:
变化前的数量变化后的数量
增长率
增长后
增长后
增长后
若连续两轮增长
增长率
下降率
下降后
下降率
下降后
下降后
若连续两轮下降
下降后
若连续两轮变化时:
增长后
变化前数量 后数量
1
练习1
某区为发展教育事业,加强了对教育经费的投入,年投入了万元,年计划投入万元. 设教育经费的年平均增长率为,根据题意,下面所列方程正确的是( ).
1
练习1
某区为发展教育事业,加强了对教育经费的投入,年投入了万元,年计划投入万元. 设教育经费的年平均增长率为,根据题意,下面所列方程正确的是( ).
1
练习1
某区为发展教育事业,加强了对教育经费的投入,年投入了万元,年计划投入万元. 设教育经费的年平均增长率为,根据题意,下面所列方程正确的是( ).
某区为发展教育事业,加强了对教育经费的投入,年投入了万元,年计划投入万元. 设教育经费的年平均增长率为,根据题意,下面所列方程正确的是( ).
1
练习1
1
练习2
某商品原价是元,经连续两次降价后售价为元,设平均每次降价的百分率为,则下面所列方程正确的是( ).
变化前数量 后数量
1
练习2
某商品原价是元,经连续两次降价后售价为元,设平均每次降价的百分率为,则下面所列方程正确的是( ).
变化前数量 后数量
1
练习2
某商品原价是元,经连续两次降价后售价为元,设平均每次降价的百分率为,则下面所列方程正确的是( ).
变化前数量 后数量
某商品原价是元,经连续两次降价后售价为元,设平均每次降价的百分率为,则下面所列方程正确的是( ).
1
练习2
变化前数量 后数量
某商品原价是元,经连续两次降价后售价为元,设平均每次降价的百分率为,则下面所列方程正确的是( ).
1
练习2
变化前数量 后数量
1
例题
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
两种药品成本的年平均下降额各是多少?
1
例题
两种药品成本的年平均下降额各是多少?
成本的年平均下降率
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
甲种药品
1
例题
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
甲种药品
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
甲种药品
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
甲种药品
乙种药品
1
例题
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
甲种药品
乙种药品
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
甲种药品
乙种药品
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两种药品成本的年平均下降额各是多少?
两年前 现在 平均下降额
甲种药品
乙种药品
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两年前 现在 平均下降额
甲种药品
乙种药品
答:甲乙药品年平均下降额分别为元、元.
两种药品成本的年平均下降额各是多少?
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
两种药品成本的年平均下降额各是多少?
答:甲乙药品年平均下降额分别为元、元.
两种药品成本的年平均下降率各是多少?哪个大?
1
例题
两种药品成本的年平均下降额各是多少?
答:甲乙药品年平均下降额分别为元、元.
两种药品成本的年平均下降率各是多少?哪个大?
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
两种药品成本的年平均下降率各是多少?哪个大?
变化前数量 后数量
1
例题
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
甲:设甲种药品成本的年平均下降率为.
则.
1
例题
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
两种药品成本的年平均下降率各是多少?哪个大?
分析
.
:整理,得
.
即 .
直接开平方,得
.
.
:整理,得
.
即 .
直接开平方,得
.
.
两种药品成本的年平均下降率各是多少?哪个大?
1
例题
甲:设甲种药品成本的年平均下降率为.
则.
解方程,得.
分析
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
甲:设甲种药品成本的年平均下降率为.
则.
解方程,得舍去.
即甲种药品成本的年平均下降率约为.
分析
两种药品成本的年平均下降率各是多少?哪个大?
1
例题
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
两种药品成本的年平均下降率各是多少?哪个大?
乙:设乙种药品成本的年平均下降率为.
则.
解方程,得舍去.
即乙种药品成本的年平均下降率约为,一样大.
分析
1
例题
两种药品成本的年平均下降率各是多少?哪个大?
乙:设乙种药品成本的年平均下降率为.
则.
解方程,得舍去.
即乙种药品成本的年平均下降率约为,一样大.
分析
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
1
例题
两种药品成本的年平均下降率各是多少?哪个大?
乙:设乙种药品成本的年平均下降率为.
则.
解方程,得舍去.
即乙种药品成本的年平均下降率约为,一样大.
分析
两年前生产吨甲种药品的成本是元,生产吨乙种药品的成本是元,随着生产技术的进步,现在生产吨甲种药品的成本是元,生产吨乙种药品的成本是元.
思考
1
2
3
经过计算,你可以得到什么结论?
成本下降额大的药品,它的成本下降率一定也大吗?
应怎样全面的比较几个对象的变化状况?
思考
1
两种药品成本的年平均下降额不同,甲为元,乙为元.
但它们的年平均下降率相同,约为.
经过计算,你可以得到什么结论?
思考
2
不一定.
乙的年平均下降额大,但年平均率和甲相同.
成本下降额大的药品,它的成本下降率一定也大吗?
思考
3
成本下降额表示绝对变化量,成本下降率表示相对变化量,两者兼顾才能全面比较对象的变化状况.
应怎样全面的比较几个对象的变化状况?
变化前数量变化后数量.
转化数学问题
阅读分析题意,建立模型,列出方程.
课
堂
小
结
转化数学问题
阅读分析题意,建立模型,列出方程.
求解数学问题
选择合适的方法求解数学问题.
解决实际问题
经过检验,找到符合题意的答案解决实际问题.
课
堂
小
结
一元二次方程是刻画现实世界中某些数量关系的有效数学模型.
课
堂
小
结
一元二次方程是刻画现实世界中某些数量关系的有效数学模型. 在运用一元二次方程分析、表达和解决实际问题的过程中,要注意体会建立数学模型解决实际问题的思想和方法.
课
堂
小
结
实际问题
一元二次方程
一元二次方程的解
实际问题的答案
数学模型
课
堂
小
结
青山村种的水稻年平均每公顷产,年平均
每公顷产,求水稻每公顷产量的年平均增长率.
某银行经过最近两次降息,使一年期存款的年利率由降
至,平均每次降息的百分率是多少结果写出的形
式,其中保留小数点后两位).
课后作业
同课章节目录
