人教版九年级数学上册2.25用列举法求概率 第1课时教学课件(共42张PPT)
文档属性
| 名称 | 人教版九年级数学上册2.25用列举法求概率 第1课时教学课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 22:50:02 | ||
图片预览










文档简介
(共42张PPT)
(第一课时)
用列举法求概率
温故知新
你知道抛掷一枚质地均匀的硬币,出现正面的概率是多少?
1
你知道抛掷一枚质地均匀的骰子,出现偶数的概率是多少?
2
你知道我手中的这枚种子发芽的概率又是多少呢?
3
温故知新
一般地,对于一个随机事件,我们把刻画其发生可能性大小的数值,称为随机事件 发生的概率,记作.
1
试验结果的有限性
每种结果的等可能性
一般地,在一次试验中,有 种可能的结果,且每种结果发生的可能性都相等,事件包含其中 种结果,则事件 发生的概率
2
温故知新
你知道抛掷一枚质地均匀的硬币,出现正面的概率是多少?
1
你知道抛掷一枚质地均匀的骰子,出现偶数的概率是多少?
2
你知道我手中的这枚种子发芽的概率又是多少呢?
3
温故知新
一般地,对于一个随机事件,我们把刻画其发生可能性大小的数值,称为随机事件 发生的概率,记作.
1
一般地,在一次试验中,有 种可能的结果,且每种结果发生的可能性都相等,事件包含其中 种结果,则事件 发生的概率
2
试验结果的有限性
每种结果的等可能性
探索新知
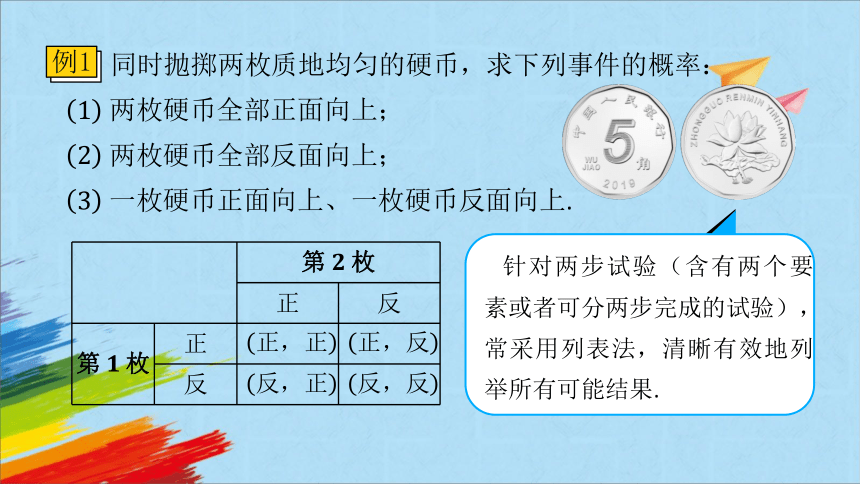
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
例1
两枚硬币全部反面向上;
一枚硬币正面向上、一枚硬币反面向上.
分析
由“一枚硬币”变“两枚”,不变的是每枚硬币的结果,变的是要素的个数.
两枚硬币全部正面向上;
两枚硬币全部正面向上;
探索新知
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
例1
解:
正正,正反,反正,反反.
所有的可能结果共有 种,且这种结果出现的可能性相等.
满足两枚硬币全部正面向上(记为事件)的结果只有一种,即“正正”,所以
列举抛掷两枚硬币可能产生的所有结果,它们是:
探索新知
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
例1
满足两枚硬币全部反面向上(记为事件)的结果只有一种,即“反反”,所以
两枚硬币全部反面向上;
一枚硬币正面向上、一枚硬币反面向上.
满足一枚硬币正面向上、一枚硬币反面向上(记为事件)的结果有两种,即“正反”“反正”,所以
针对两步试验(含有两个要素或者可分两步完成的试验),常采用列表法,清晰有效地列举所有可能结果.
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
例1
两枚硬币全部反面向上;
一枚硬币正面向上、一枚硬币反面向上.
两枚硬币全部正面向上;
第枚 正 反
第枚 正
反
探索新知
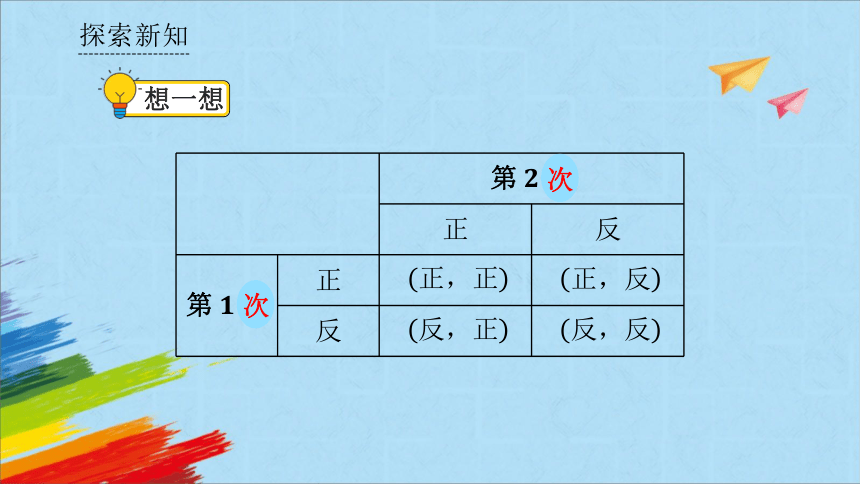
将试验变为“先后两次抛掷一枚质地均匀的硬币”, 试验的所有可能结果和所求概率会有变化吗?
想一想
探索新知
第枚 正 反
第枚 正
反
想一想
次
次
探索新知
将试验变为“先后两次抛掷一枚质地均匀的硬币”, 试验的所有可能结果和所求概率会有变化吗?
想一想
没有变化!
基础巩固
同时抛掷两枚质地均匀的骰子,计算下列事件概率:
练习
两枚骰子点数的和为;
至少有一枚骰子的点数为奇数.
分析
可采用的方法有:
直接列举法,列表法.
两枚骰子的点数相同;
解:两枚骰子分别记作第枚和第 枚,列表如下:
第枚
第 枚
试验的可能结果共种,且每种结果出现的可能性相等.
解:两枚骰子分别记作第枚和第 枚,列表如下:
第枚
第 枚
试验的可能结果共种,且每种结果出现的可能性相等.
两枚骰子点数相同(记为事件),结果有 种,所以
解:两枚骰子分别记作第枚和第 枚,列表如下:
第枚
第 枚
两枚骰子点数和为(记为事件)的结果有 种,即
, , , ,所以
至少有一枚骰子点数为奇数(记为事件),即一枚是奇数或者两枚都是奇数.
第枚
第 枚
至少有一枚骰子点数为奇数(记为事件),即一枚是奇数或者两枚都是奇数.
第枚
第 枚
至少有一枚骰子点数为奇数(记为事件),即一枚是奇数或者两枚都是奇数.
第枚
第 枚
符合条件的结果有 种.
第枚
第 枚
第枚
第 枚
第枚
第 枚
至少有一枚骰子点数为奇数(记为事件),即一枚是奇数或者两枚都是奇数,符合条件的结果有 种,即
第枚
第 枚
两枚骰子可能出现的结果:
两枚是奇数
1
分析
一枚是奇数一枚是偶数
2
枚是奇数(都是偶数)
3
第枚
第 枚
两枚骰子可能出现的结果:
两枚是奇数
1
分析
一枚是奇数一枚是偶数
2
枚是奇数(都是偶数)
3
第枚
第 枚
至少有一枚是奇数
第枚
第 枚
至少一枚点数是奇数,即除了两个都是偶数的情况.
,,
第枚 奇 偶
第枚 奇
偶
第枚 奇 偶
第枚 奇
偶
第枚 奇 偶
第枚 奇
偶
至少一枚点数是奇数的结果有 , , ,所以
知识小结
当一次试验涉及两个要素(如:抛掷两枚硬币、两枚骰子)或一个要素做两次试验(如:一枚硬币或一枚骰子先后抛掷两次),可称该试验为两步试验. 针对这种两步试验,当可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
1
直接法列举结果应有序,方可不重不漏.
2
列举时,注意换个角度想问题,则可化繁为简.
3
深化理解
例2
分析
归类定型是关键,摸了一次球后放回,两次摸球互不影响,对比该试验与先后抛掷一枚硬币这一基本的试验模型,都是分两步,每步结果都是等可能的,两步之间互不影响,唯一不同是结果的个数,看来两者属于同一模型.
一个不透明的口袋中有 个完全相同的小球,分别标号为随机摸出一个球,记录标号后放回,再随机摸出一个球,求两个球标号之差为 的概率.
解:根据题意,列表如下:
第次
第 次
摸出的两球共有 种可能结果,且每种结果等可能性出现.
解:根据题意,列表如下:
第次
第 次
摸出的两球共有 种可能结果,且每种结果等可能性出现.
满足两球标号差为(记为事件 )的结果有种:
,
深化理解
分析
“放回”与“不放回”试验的结果会有所不同吗?
“放回”型问题,两次操作(两个要素)间互不影响,而该问题中,若第一次拿出号球,第二次受第一次操作的影响,就不可能再拿出 号球,结果中不存在相同标号.
一个不透明的口袋中有 个完全相同的小球,分别标号为随机摸出一个球记录标号后,不放回,再随机摸出一个球,求两个球标号之差为 的概率.
练习
解:
第次
第 次
不放回拿两次球,所有可能结果共种(例 表格中去掉两球标号相同的部分).
解:
第次
第 次
其中,两球标号差为(设为事件)的结果有种,即 所以
不放回拿两次球,所有可能结果共种(例 表格中去掉两球标号相同的部分).
灵活应用
分析
该问题可归结为一个两步试验,第一步明明 选车,第二步宁宁 选车. 两人都得有车坐.
有三辆车按照编号,明明和宁宁两人可任意选坐一辆车,从学校去少年宫表演,则两人同坐 号车的概率是多少?
练习
解:可列表列举两人坐车的所有可能结果,
选的车
选 的 车
( 表示明明坐 号车,同时宁宁坐 号车.)
可能出现的结果共有 种,且每种结果出现的可能性相等.
根据题意,两人同坐 号车有一种结果,即 所以,
课
堂
小
结
1
投掷两枚硬币试验模型的特征及求概率的方法.
摸球试验模型中“放回”与“不放回”的区别.
2
列举试验结果的两种方法:直接列举法和列表法.
对比学习的方法,不断将新问题归型转化为旧问题.
课后作业
不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个. 求下列事件的概率:
1
第一次摸到红球,第二次摸到绿球;
两次都摸到相同颜色的小球;
两次摸到的球中,一个绿球,一个红球.
课后作业
不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,不放回,再随机从中摸出一个. 求下列事件的概率:
2
有两把不同的锁和三把钥匙,其中两把钥匙分别能打开这两把锁,第三把钥匙不能打开这两把锁,随机取出一把钥匙开任意一把锁,一次打开锁的概率是多少?
3
第一次摸到红球,第二次摸到绿球;
两次摸到的球中,一个绿球,一个红球.
(第一课时)
用列举法求概率
温故知新
你知道抛掷一枚质地均匀的硬币,出现正面的概率是多少?
1
你知道抛掷一枚质地均匀的骰子,出现偶数的概率是多少?
2
你知道我手中的这枚种子发芽的概率又是多少呢?
3
温故知新
一般地,对于一个随机事件,我们把刻画其发生可能性大小的数值,称为随机事件 发生的概率,记作.
1
试验结果的有限性
每种结果的等可能性
一般地,在一次试验中,有 种可能的结果,且每种结果发生的可能性都相等,事件包含其中 种结果,则事件 发生的概率
2
温故知新
你知道抛掷一枚质地均匀的硬币,出现正面的概率是多少?
1
你知道抛掷一枚质地均匀的骰子,出现偶数的概率是多少?
2
你知道我手中的这枚种子发芽的概率又是多少呢?
3
温故知新
一般地,对于一个随机事件,我们把刻画其发生可能性大小的数值,称为随机事件 发生的概率,记作.
1
一般地,在一次试验中,有 种可能的结果,且每种结果发生的可能性都相等,事件包含其中 种结果,则事件 发生的概率
2
试验结果的有限性
每种结果的等可能性
探索新知
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
例1
两枚硬币全部反面向上;
一枚硬币正面向上、一枚硬币反面向上.
分析
由“一枚硬币”变“两枚”,不变的是每枚硬币的结果,变的是要素的个数.
两枚硬币全部正面向上;
两枚硬币全部正面向上;
探索新知
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
例1
解:
正正,正反,反正,反反.
所有的可能结果共有 种,且这种结果出现的可能性相等.
满足两枚硬币全部正面向上(记为事件)的结果只有一种,即“正正”,所以
列举抛掷两枚硬币可能产生的所有结果,它们是:
探索新知
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
例1
满足两枚硬币全部反面向上(记为事件)的结果只有一种,即“反反”,所以
两枚硬币全部反面向上;
一枚硬币正面向上、一枚硬币反面向上.
满足一枚硬币正面向上、一枚硬币反面向上(记为事件)的结果有两种,即“正反”“反正”,所以
针对两步试验(含有两个要素或者可分两步完成的试验),常采用列表法,清晰有效地列举所有可能结果.
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
例1
两枚硬币全部反面向上;
一枚硬币正面向上、一枚硬币反面向上.
两枚硬币全部正面向上;
第枚 正 反
第枚 正
反
探索新知
将试验变为“先后两次抛掷一枚质地均匀的硬币”, 试验的所有可能结果和所求概率会有变化吗?
想一想
探索新知
第枚 正 反
第枚 正
反
想一想
次
次
探索新知
将试验变为“先后两次抛掷一枚质地均匀的硬币”, 试验的所有可能结果和所求概率会有变化吗?
想一想
没有变化!
基础巩固
同时抛掷两枚质地均匀的骰子,计算下列事件概率:
练习
两枚骰子点数的和为;
至少有一枚骰子的点数为奇数.
分析
可采用的方法有:
直接列举法,列表法.
两枚骰子的点数相同;
解:两枚骰子分别记作第枚和第 枚,列表如下:
第枚
第 枚
试验的可能结果共种,且每种结果出现的可能性相等.
解:两枚骰子分别记作第枚和第 枚,列表如下:
第枚
第 枚
试验的可能结果共种,且每种结果出现的可能性相等.
两枚骰子点数相同(记为事件),结果有 种,所以
解:两枚骰子分别记作第枚和第 枚,列表如下:
第枚
第 枚
两枚骰子点数和为(记为事件)的结果有 种,即
, , , ,所以
至少有一枚骰子点数为奇数(记为事件),即一枚是奇数或者两枚都是奇数.
第枚
第 枚
至少有一枚骰子点数为奇数(记为事件),即一枚是奇数或者两枚都是奇数.
第枚
第 枚
至少有一枚骰子点数为奇数(记为事件),即一枚是奇数或者两枚都是奇数.
第枚
第 枚
符合条件的结果有 种.
第枚
第 枚
第枚
第 枚
第枚
第 枚
至少有一枚骰子点数为奇数(记为事件),即一枚是奇数或者两枚都是奇数,符合条件的结果有 种,即
第枚
第 枚
两枚骰子可能出现的结果:
两枚是奇数
1
分析
一枚是奇数一枚是偶数
2
枚是奇数(都是偶数)
3
第枚
第 枚
两枚骰子可能出现的结果:
两枚是奇数
1
分析
一枚是奇数一枚是偶数
2
枚是奇数(都是偶数)
3
第枚
第 枚
至少有一枚是奇数
第枚
第 枚
至少一枚点数是奇数,即除了两个都是偶数的情况.
,,
第枚 奇 偶
第枚 奇
偶
第枚 奇 偶
第枚 奇
偶
第枚 奇 偶
第枚 奇
偶
至少一枚点数是奇数的结果有 , , ,所以
知识小结
当一次试验涉及两个要素(如:抛掷两枚硬币、两枚骰子)或一个要素做两次试验(如:一枚硬币或一枚骰子先后抛掷两次),可称该试验为两步试验. 针对这种两步试验,当可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
1
直接法列举结果应有序,方可不重不漏.
2
列举时,注意换个角度想问题,则可化繁为简.
3
深化理解
例2
分析
归类定型是关键,摸了一次球后放回,两次摸球互不影响,对比该试验与先后抛掷一枚硬币这一基本的试验模型,都是分两步,每步结果都是等可能的,两步之间互不影响,唯一不同是结果的个数,看来两者属于同一模型.
一个不透明的口袋中有 个完全相同的小球,分别标号为随机摸出一个球,记录标号后放回,再随机摸出一个球,求两个球标号之差为 的概率.
解:根据题意,列表如下:
第次
第 次
摸出的两球共有 种可能结果,且每种结果等可能性出现.
解:根据题意,列表如下:
第次
第 次
摸出的两球共有 种可能结果,且每种结果等可能性出现.
满足两球标号差为(记为事件 )的结果有种:
,
深化理解
分析
“放回”与“不放回”试验的结果会有所不同吗?
“放回”型问题,两次操作(两个要素)间互不影响,而该问题中,若第一次拿出号球,第二次受第一次操作的影响,就不可能再拿出 号球,结果中不存在相同标号.
一个不透明的口袋中有 个完全相同的小球,分别标号为随机摸出一个球记录标号后,不放回,再随机摸出一个球,求两个球标号之差为 的概率.
练习
解:
第次
第 次
不放回拿两次球,所有可能结果共种(例 表格中去掉两球标号相同的部分).
解:
第次
第 次
其中,两球标号差为(设为事件)的结果有种,即 所以
不放回拿两次球,所有可能结果共种(例 表格中去掉两球标号相同的部分).
灵活应用
分析
该问题可归结为一个两步试验,第一步明明 选车,第二步宁宁 选车. 两人都得有车坐.
有三辆车按照编号,明明和宁宁两人可任意选坐一辆车,从学校去少年宫表演,则两人同坐 号车的概率是多少?
练习
解:可列表列举两人坐车的所有可能结果,
选的车
选 的 车
( 表示明明坐 号车,同时宁宁坐 号车.)
可能出现的结果共有 种,且每种结果出现的可能性相等.
根据题意,两人同坐 号车有一种结果,即 所以,
课
堂
小
结
1
投掷两枚硬币试验模型的特征及求概率的方法.
摸球试验模型中“放回”与“不放回”的区别.
2
列举试验结果的两种方法:直接列举法和列表法.
对比学习的方法,不断将新问题归型转化为旧问题.
课后作业
不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个. 求下列事件的概率:
1
第一次摸到红球,第二次摸到绿球;
两次都摸到相同颜色的小球;
两次摸到的球中,一个绿球,一个红球.
课后作业
不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,不放回,再随机从中摸出一个. 求下列事件的概率:
2
有两把不同的锁和三把钥匙,其中两把钥匙分别能打开这两把锁,第三把钥匙不能打开这两把锁,随机取出一把钥匙开任意一把锁,一次打开锁的概率是多少?
3
第一次摸到红球,第二次摸到绿球;
两次摸到的球中,一个绿球,一个红球.
同课章节目录
