人教版九年级数学上册《用频率估计概率》第1课时 课件(共33张PPT)
文档属性
| 名称 | 人教版九年级数学上册《用频率估计概率》第1课时 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 21:48:51 | ||
图片预览






文档简介
(共33张PPT)
用频率估计概率
(第一课时)
情境引入
出现“正面朝上”和“反面朝上”两种情况
都是
抛掷一枚质地均匀的硬币,硬币落地后,会出现哪些可能的结果呢?
问题1
它们的概率是多少呢?
问题2
在多次抛掷一枚质地均匀的硬币时,会出现什么情况呢?
问题3
试验探究
抛硬币试验(小组活动)
累计抛掷次数
“正面朝上”的频数
“正面朝上”的频率
同学们 人组成小组,抛掷一枚质地均匀硬币次,每隔次记录“正面朝上”的次数,并算出“正面朝上”的频率,完成下表:
试验探究
抛硬币试验(小组活动)
试验要求
抛掷硬币的同学,需要将手臂举到一定高度,让硬币自由落下,当硬币落地时,观察并报告试验结果;
1
负责记录的同学,请选择一种适当的方法记录数据;
2
负责监督的同学,尽可能保证每次试验的条件是相同的,确保试验结果的随机性.
3
试验探究
抛硬币试验(小组活动)
累计抛掷次数
“正面朝上”的频数
“正面朝上”的频率
同学们 人组成小组,抛掷一枚质地均匀硬币次,每隔次记录“正面朝上”的次数,并算出“正面朝上”的频率,完成下表:
试验探究
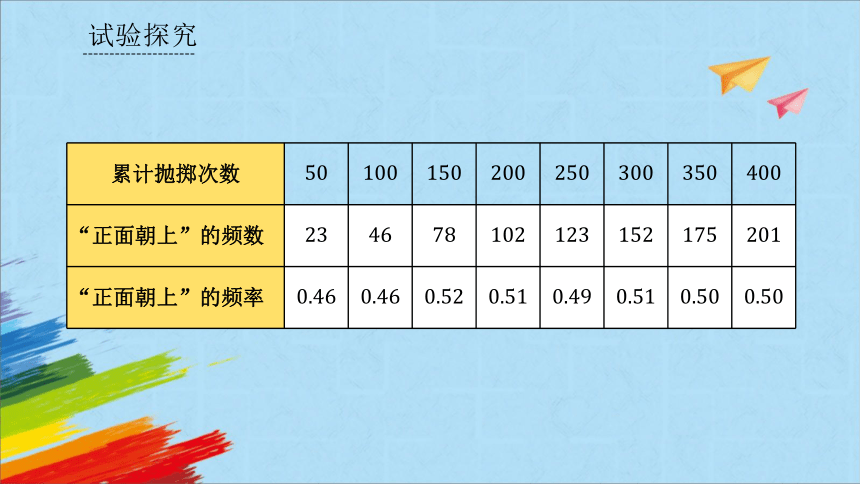
累计抛掷次数
“正面朝上”的频数
“正面朝上”的频率
试验探究
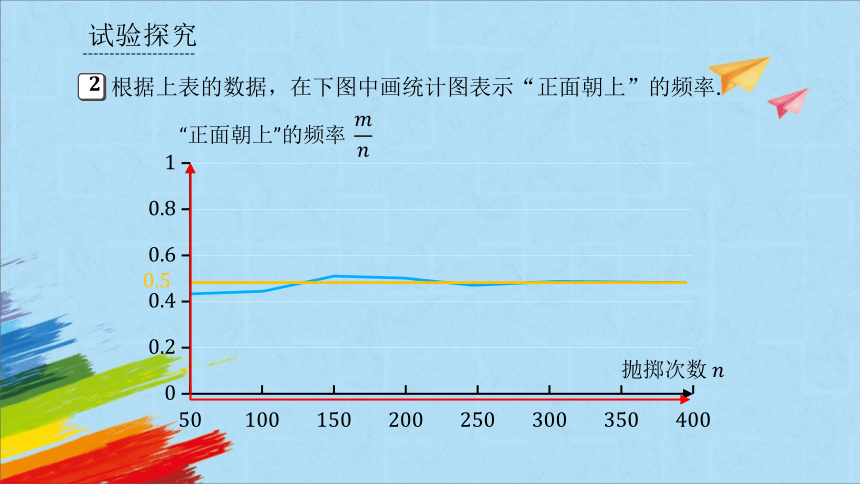
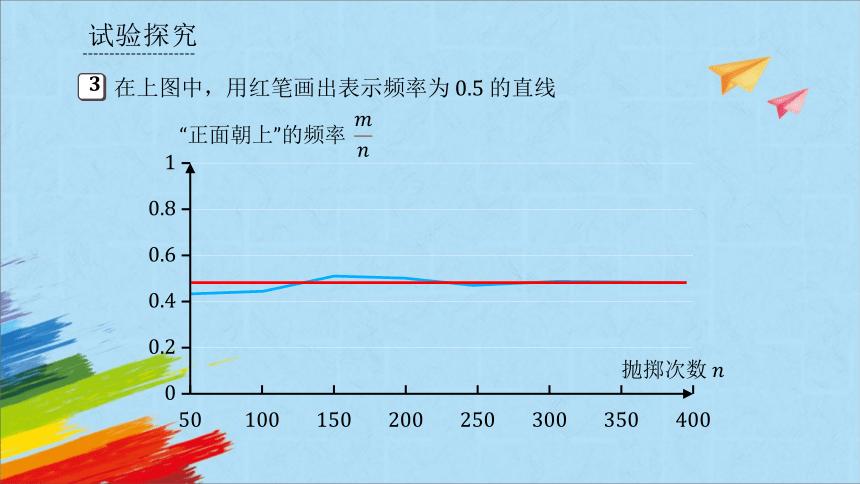
根据上表的数据,在下图中画统计图表示“正面朝上”的频率.
抛掷次数
试验探究
抛掷次数
试验探究
随着抛掷次数的增加,“正面向上”的频率的变化趋势是什么
思考
试验探究
思考:随着抛掷次数的增加,“正面向上”的频率的变化趋势是什么
可以发现,在重复抛掷一枚硬币,“正面向上”的频率在 附近摆动.
一般的,随着抛掷次数的增加,频率呈现出一定的稳定性:在 附近摆动的幅度会越来越小.
这时,我们称“正面向上”的频率稳定于. 它与前面用列举法得出的“正面向上”的概率是同一个数值.
试验探究
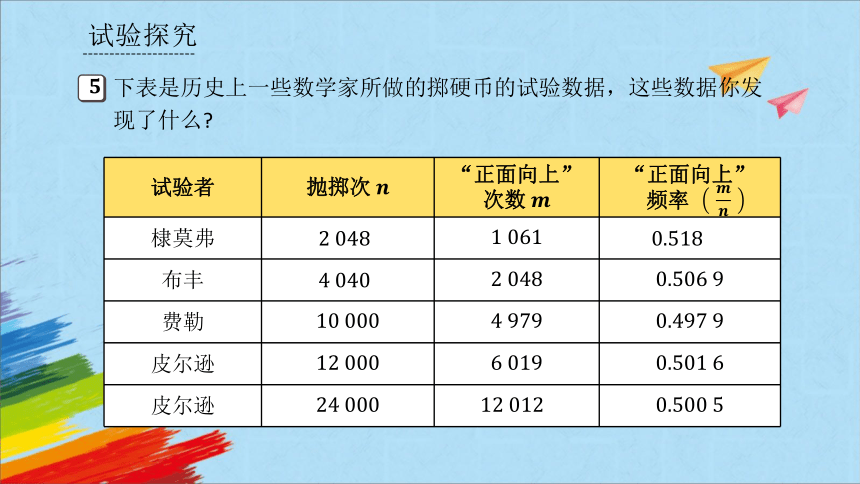
下表是历史上一些数学家所做的掷硬币的试验数据,这些数据你发现了什么
试验者 抛掷次 “正面向上” 次数 “正面向上”
频率
棣莫弗
布丰
费勒
皮尔逊
皮尔逊
试验探究
在抛掷一枚硬币时,结果不是“正面向上”,就是“反面向上”.
因此,从上面的试验中也能得到相应的“反面向上”的频率.
当“正面向上”的频率稳定于 时,“反面向上”的频率也稳定于. 它也与前面用列举法得出的“反面向上”的概率是同一个数值.
下表是历史上一些数学家所做的掷硬币的试验数据,这些数据你发现了什么
通过大量重复试验,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性. 因此可以用随机事件发生的频率来估计该事件发生的概率.
归纳小结
通过大量重复试验,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性.
试验结论
探究思考
思考1
抛掷硬币试验的特点?
1
2
可能出现的结果数 ;
每种可能结果的可能性 .
有限
相等
答案是否定的. 我们无法用列举法求出概率,因为我们无法判断“结果是否具有等可能性”.
探究思考
思考2
如果是抛掷图钉的试验,能否用列举法求出概率?
答案是否定的.
思考3
能不能用频率估计概率?
试验探究
图钉落地的试验(小组活动)
从一定高度落下的图钉,着地时会有哪些可能的结果
问题
钉尖朝上
钉尖着地
出现“钉尖朝上”和“钉尖着地”两种情况
试验探究
抛掷一枚图钉 次,每隔 次记录相应的数据,完成下表:
试验累计次数
钉尖朝上的次数
钉尖朝上的频率
图钉落地的试验(小组活动)
钉尖朝上的次数
钉尖朝上的频率
试验探究
试验要求
负责抛掷的同学,需要水平拿着图钉,在视线处让图钉自由落下,当图钉落地时观察并汇报试验结果;
1
负责记录的同学,需要选择一种合理的记录方式记录数据,比如画正字的方法;
2
负责监督的同学,尽可能地保证每次试验条件是相同的,尽可能保证试验的随机性.
3
图钉落地的试验(小组活动)
试验探究
抛掷一枚图钉 次,每隔 次记录相应的数据,完成下表:
试验累计次数
钉尖朝上的次数
钉尖朝上的频率
图钉落地的试验(小组活动)
试验累计次数
钉尖朝上的次数
钉尖朝上的频率
试验探究
试验探究
根据上表画出统计图表示“”的频率.
抛掷次数
试验探究
这个试验你得到了什么结论?
在图钉落地试验中,随着试验次数的增加,“钉尖朝上”的频率稳定在常数 附近.
试验结论
可以发现,在重复抛掷一枚图钉时,“钉尖朝上”的频率在 附近摆动.
一般的,随着抛掷次数的增加,频率呈现出一定的稳定性:
在附近摆动的幅度会越来越小.
这时,我们称“钉尖朝上”的频率稳定于 .
试验探究
同时,我们也得出了抛掷图钉产生的两种情况出现的可能性不相等.
这个试验你得到了什么结论?
课堂小结
通过大量重复试验,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性. 因此可以用随机事件发生的频率来估计该事件发生的概率.
课
堂
小
结
通过大量重复试验,随着试验次数的增加,一个事件出现的频率,
总在一个固定数的附近摆动,显示出一定的稳定性.
但大量重复试验所得结果却能反应客观规律. 这称为大
数法则,亦称大数定律.
但大量重复试验所得结果却能反应客观规律.
数学史实
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,
每次测得的结果虽不尽相同,
大数法则
试验者 抛掷次 “正面向上” 次数 “正面向上”
频率
棣莫弗
布丰
费勒
皮尔逊
皮尔逊
数学史实
对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总是在一个固定数的附近摆动,那么这个频率就无限接近于这个事件的概率.
数学史实
——伯努利
雅各布第一·伯努利
数学史实
年出生于瑞士巴塞尔
书中对频率的稳定性规律进行了严格的证明,是历史上第一次对“频率稳定于概率”论断给出的数学证明,
年卒于瑞士巴塞尔
年出版他的遗著《猜度术》
它揭示了因偶然性的作用而呈现的杂乱无章现象中的一种规律性.
书中对频率的稳定性规律进行了严格的证明,
棣莫弗
数学史实
年,他在英国皇家学会的《哲学学报》上发表了《抽签的测量》;
年,该文用英文出版时翻译成
《机会的学说》,并扩充成一本书.
棣莫弗是法国数学家. 棣莫弗在雅各布·伯努利的《猜度术》出版之前,就对概率论进行了广泛而深入的研究.
费勒对概率论及其应用作出了贡献.
费勒是美国数学家.
费勒
数学史实
其著作《概率论及其应用引导》已被译成中文,由科学出版社 年出版.
课后作业
下表记录了一名球员在罚球线上投篮的结果
这名球员投篮一次,投中的概率约是多少(结果保留小数点后一位)
投篮次数
投中次数
投中频率
计算投中频率(结果保留小数点后两位);
课后作业
用前面抛掷硬币的试验方法,请你自己设计并完成掷骰子的试验,估计掷一次骰子时“点数是 ”的概率.
用频率估计概率
(第一课时)
情境引入
出现“正面朝上”和“反面朝上”两种情况
都是
抛掷一枚质地均匀的硬币,硬币落地后,会出现哪些可能的结果呢?
问题1
它们的概率是多少呢?
问题2
在多次抛掷一枚质地均匀的硬币时,会出现什么情况呢?
问题3
试验探究
抛硬币试验(小组活动)
累计抛掷次数
“正面朝上”的频数
“正面朝上”的频率
同学们 人组成小组,抛掷一枚质地均匀硬币次,每隔次记录“正面朝上”的次数,并算出“正面朝上”的频率,完成下表:
试验探究
抛硬币试验(小组活动)
试验要求
抛掷硬币的同学,需要将手臂举到一定高度,让硬币自由落下,当硬币落地时,观察并报告试验结果;
1
负责记录的同学,请选择一种适当的方法记录数据;
2
负责监督的同学,尽可能保证每次试验的条件是相同的,确保试验结果的随机性.
3
试验探究
抛硬币试验(小组活动)
累计抛掷次数
“正面朝上”的频数
“正面朝上”的频率
同学们 人组成小组,抛掷一枚质地均匀硬币次,每隔次记录“正面朝上”的次数,并算出“正面朝上”的频率,完成下表:
试验探究
累计抛掷次数
“正面朝上”的频数
“正面朝上”的频率
试验探究
根据上表的数据,在下图中画统计图表示“正面朝上”的频率.
抛掷次数
试验探究
抛掷次数
试验探究
随着抛掷次数的增加,“正面向上”的频率的变化趋势是什么
思考
试验探究
思考:随着抛掷次数的增加,“正面向上”的频率的变化趋势是什么
可以发现,在重复抛掷一枚硬币,“正面向上”的频率在 附近摆动.
一般的,随着抛掷次数的增加,频率呈现出一定的稳定性:在 附近摆动的幅度会越来越小.
这时,我们称“正面向上”的频率稳定于. 它与前面用列举法得出的“正面向上”的概率是同一个数值.
试验探究
下表是历史上一些数学家所做的掷硬币的试验数据,这些数据你发现了什么
试验者 抛掷次 “正面向上” 次数 “正面向上”
频率
棣莫弗
布丰
费勒
皮尔逊
皮尔逊
试验探究
在抛掷一枚硬币时,结果不是“正面向上”,就是“反面向上”.
因此,从上面的试验中也能得到相应的“反面向上”的频率.
当“正面向上”的频率稳定于 时,“反面向上”的频率也稳定于. 它也与前面用列举法得出的“反面向上”的概率是同一个数值.
下表是历史上一些数学家所做的掷硬币的试验数据,这些数据你发现了什么
通过大量重复试验,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性. 因此可以用随机事件发生的频率来估计该事件发生的概率.
归纳小结
通过大量重复试验,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性.
试验结论
探究思考
思考1
抛掷硬币试验的特点?
1
2
可能出现的结果数 ;
每种可能结果的可能性 .
有限
相等
答案是否定的. 我们无法用列举法求出概率,因为我们无法判断“结果是否具有等可能性”.
探究思考
思考2
如果是抛掷图钉的试验,能否用列举法求出概率?
答案是否定的.
思考3
能不能用频率估计概率?
试验探究
图钉落地的试验(小组活动)
从一定高度落下的图钉,着地时会有哪些可能的结果
问题
钉尖朝上
钉尖着地
出现“钉尖朝上”和“钉尖着地”两种情况
试验探究
抛掷一枚图钉 次,每隔 次记录相应的数据,完成下表:
试验累计次数
钉尖朝上的次数
钉尖朝上的频率
图钉落地的试验(小组活动)
钉尖朝上的次数
钉尖朝上的频率
试验探究
试验要求
负责抛掷的同学,需要水平拿着图钉,在视线处让图钉自由落下,当图钉落地时观察并汇报试验结果;
1
负责记录的同学,需要选择一种合理的记录方式记录数据,比如画正字的方法;
2
负责监督的同学,尽可能地保证每次试验条件是相同的,尽可能保证试验的随机性.
3
图钉落地的试验(小组活动)
试验探究
抛掷一枚图钉 次,每隔 次记录相应的数据,完成下表:
试验累计次数
钉尖朝上的次数
钉尖朝上的频率
图钉落地的试验(小组活动)
试验累计次数
钉尖朝上的次数
钉尖朝上的频率
试验探究
试验探究
根据上表画出统计图表示“”的频率.
抛掷次数
试验探究
这个试验你得到了什么结论?
在图钉落地试验中,随着试验次数的增加,“钉尖朝上”的频率稳定在常数 附近.
试验结论
可以发现,在重复抛掷一枚图钉时,“钉尖朝上”的频率在 附近摆动.
一般的,随着抛掷次数的增加,频率呈现出一定的稳定性:
在附近摆动的幅度会越来越小.
这时,我们称“钉尖朝上”的频率稳定于 .
试验探究
同时,我们也得出了抛掷图钉产生的两种情况出现的可能性不相等.
这个试验你得到了什么结论?
课堂小结
通过大量重复试验,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性. 因此可以用随机事件发生的频率来估计该事件发生的概率.
课
堂
小
结
通过大量重复试验,随着试验次数的增加,一个事件出现的频率,
总在一个固定数的附近摆动,显示出一定的稳定性.
但大量重复试验所得结果却能反应客观规律. 这称为大
数法则,亦称大数定律.
但大量重复试验所得结果却能反应客观规律.
数学史实
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,
每次测得的结果虽不尽相同,
大数法则
试验者 抛掷次 “正面向上” 次数 “正面向上”
频率
棣莫弗
布丰
费勒
皮尔逊
皮尔逊
数学史实
对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总是在一个固定数的附近摆动,那么这个频率就无限接近于这个事件的概率.
数学史实
——伯努利
雅各布第一·伯努利
数学史实
年出生于瑞士巴塞尔
书中对频率的稳定性规律进行了严格的证明,是历史上第一次对“频率稳定于概率”论断给出的数学证明,
年卒于瑞士巴塞尔
年出版他的遗著《猜度术》
它揭示了因偶然性的作用而呈现的杂乱无章现象中的一种规律性.
书中对频率的稳定性规律进行了严格的证明,
棣莫弗
数学史实
年,他在英国皇家学会的《哲学学报》上发表了《抽签的测量》;
年,该文用英文出版时翻译成
《机会的学说》,并扩充成一本书.
棣莫弗是法国数学家. 棣莫弗在雅各布·伯努利的《猜度术》出版之前,就对概率论进行了广泛而深入的研究.
费勒对概率论及其应用作出了贡献.
费勒是美国数学家.
费勒
数学史实
其著作《概率论及其应用引导》已被译成中文,由科学出版社 年出版.
课后作业
下表记录了一名球员在罚球线上投篮的结果
这名球员投篮一次,投中的概率约是多少(结果保留小数点后一位)
投篮次数
投中次数
投中频率
计算投中频率(结果保留小数点后两位);
课后作业
用前面抛掷硬币的试验方法,请你自己设计并完成掷骰子的试验,估计掷一次骰子时“点数是 ”的概率.
同课章节目录
