人教版九年级数学上册2.25用列举法求概率 第2课时教学课件(共53张PPT)
文档属性
| 名称 | 人教版九年级数学上册2.25用列举法求概率 第2课时教学课件(共53张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 22:52:31 | ||
图片预览




文档简介
(共53张PPT)
(第二课时)
用列举法求概率
应用旧方法,解决新问题
分析
列表法已经难以胜任(表格是二维的,不便于加入第三枚硬币情况),还有什么方法列举结果呢?
引例
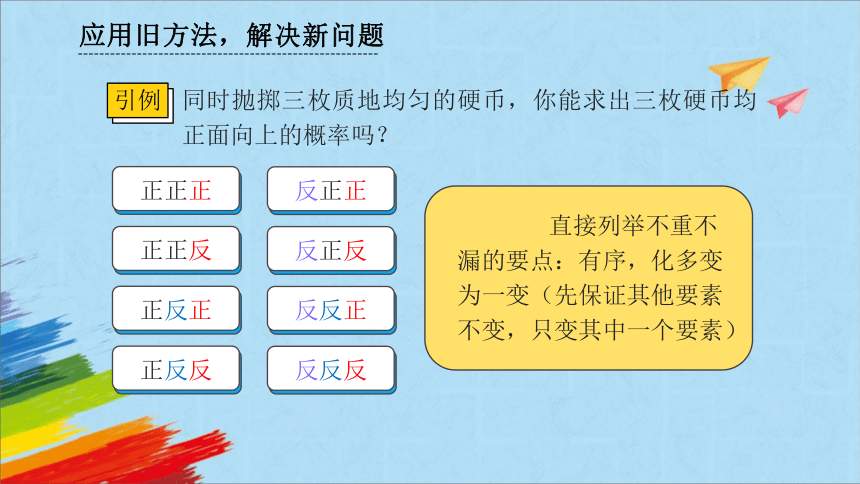
同时抛掷三枚质地均匀的硬币,你能求出三枚硬币均正面向上的概率吗?
应用旧方法,解决新问题
直接列举不重不漏的要点:有序,化多变为一变(先保证其他要素不变,只变其中一个要素)
引例
同时抛掷三枚质地均匀的硬币,你能求出三枚硬币均正面向上的概率吗?
正正正
正正反
正反正
正反反
反正正
反正反
反反正
反反反
应用旧方法,解决新问题
引例
同时抛掷三枚质地均匀的硬币,你能求出三枚硬币均正面向上的概率吗?
解:同时抛掷三枚硬币,所有可能的结果有种,即正正正,正正反,正反正,正反反,反正正,反正反,反反正,反反反. 其中,三枚硬币均正面向上(设为事件 )的结果仅有种,即正正正,所以
学用新方法,清晰又省力
分析
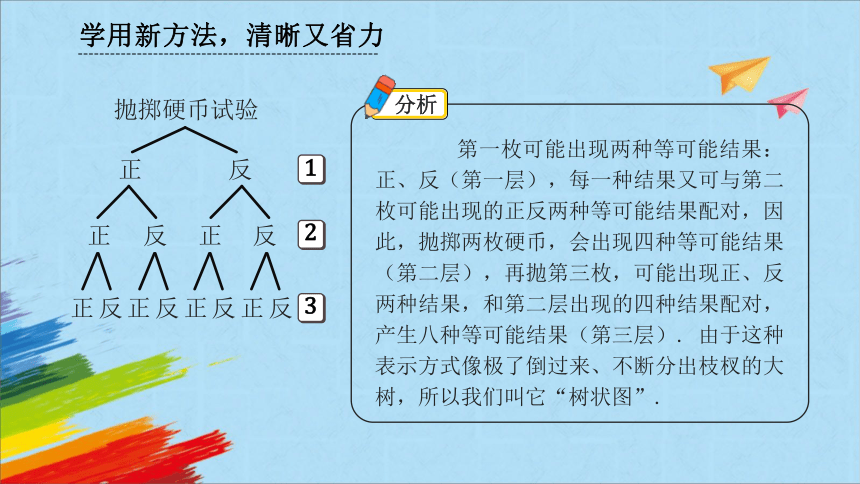
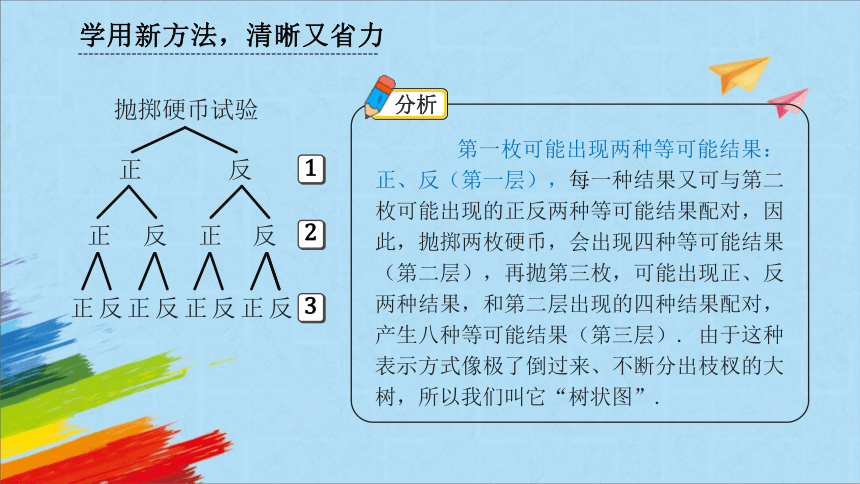
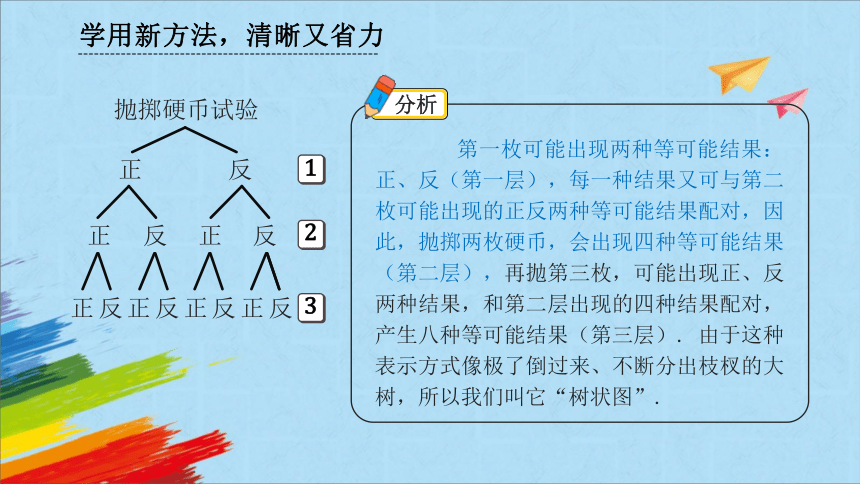
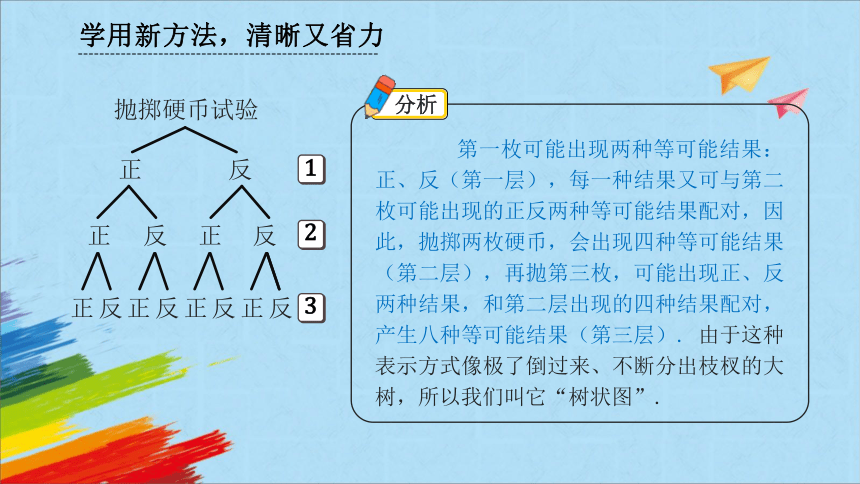
第一枚可能出现两种等可能结果:正、反(第一层),每一种结果又可与第二枚可能出现的正反两种等可能结果配对,因此,抛掷两枚硬币,会出现四种等可能结果(第二层),再抛第三枚,可能出现正、反两种结果,和第二层出现的四种结果配对,产生八种等可能结果(第三层). 由于这种表示方式像极了倒过来、不断分出枝杈的大树,所以我们叫它“树状图”.
抛掷硬币试验
正
反
正
反
正
反
正
反
正
反
正
反
正
反
1
2
3
学用新方法,清晰又省力
分析
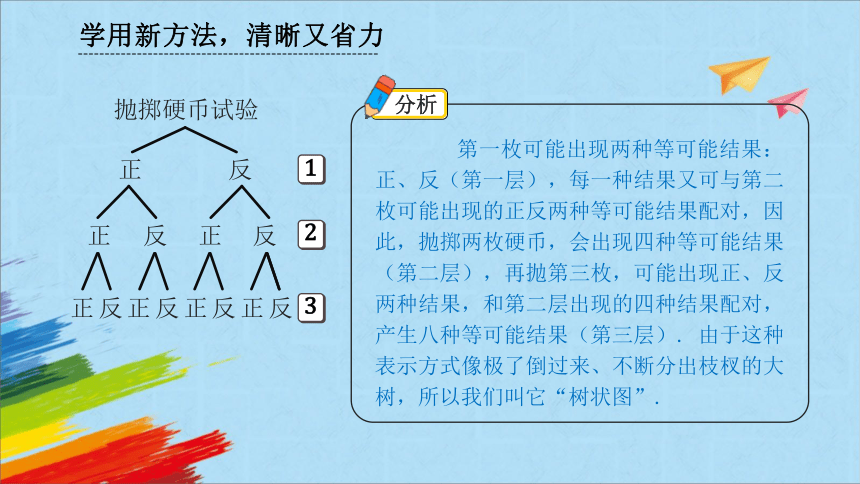
第一枚可能出现两种等可能结果:正、反(第一层),每一种结果又可与第二枚可能出现的正反两种等可能结果配对,因此,抛掷两枚硬币,会出现四种等可能结果(第二层),再抛第三枚,可能出现正、反两种结果,和第二层出现的四种结果配对,产生八种等可能结果(第三层). 由于这种表示方式像极了倒过来、不断分出枝杈的大树,所以我们叫它“树状图”.
抛掷硬币试验
正
反
正
反
正
反
正
反
正
反
正
反
正
反
1
2
3
学用新方法,清晰又省力
分析
第一枚可能出现两种等可能结果:正、反(第一层),每一种结果又可与第二枚可能出现的正反两种等可能结果配对,因此,抛掷两枚硬币,会出现四种等可能结果(第二层),再抛第三枚,可能出现正、反两种结果,和第二层出现的四种结果配对,产生八种等可能结果(第三层). 由于这种表示方式像极了倒过来、不断分出枝杈的大树,所以我们叫它“树状图”.
抛掷硬币试验
正
反
正
反
正
反
正
反
正
反
正
反
正
反
1
2
3
学用新方法,清晰又省力
分析
第一枚可能出现两种等可能结果:正、反(第一层),每一种结果又可与第二枚可能出现的正反两种等可能结果配对,因此,抛掷两枚硬币,会出现四种等可能结果(第二层),再抛第三枚,可能出现正、反两种结果,和第二层出现的四种结果配对,产生八种等可能结果(第三层). 由于这种表示方式像极了倒过来、不断分出枝杈的大树,所以我们叫它“树状图”.
抛掷硬币试验
正
反
正
反
正
反
正
反
正
反
正
反
正
反
1
2
3
学用新方法,清晰又省力
分析
第一枚可能出现两种等可能结果:正、反(第一层),每一种结果又可与第二枚可能出现的正反两种等可能结果配对,因此,抛掷两枚硬币,会出现四种等可能结果(第二层),再抛第三枚,可能出现正、反两种结果,和第二层出现的四种结果配对,产生八种等可能结果(第三层). 由于这种表示方式像极了倒过来、不断分出枝杈的大树,所以我们叫它“树状图”.
抛掷硬币试验
正
反
正
反
正
反
正
反
正
反
正
反
正
反
1
2
3
学用新方法,清晰又省力
分析
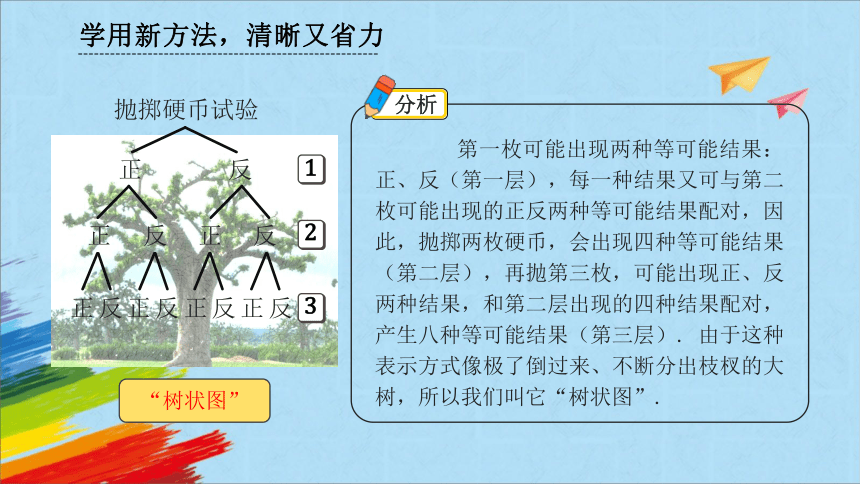
第一枚可能出现两种等可能结果:正、反(第一层),每一种结果又可与第二枚可能出现的正反两种等可能结果配对,因此,抛掷两枚硬币,会出现四种等可能结果(第二层),再抛第三枚,可能出现正、反两种结果,和第二层出现的四种结果配对,产生八种等可能结果(第三层). 由于这种表示方式像极了倒过来、不断分出枝杈的大树,所以我们叫它“树状图”.
抛掷硬币试验
正
反
正
反
正
反
正
反
正
反
正
反
正
反
“树状图”
1
2
3
学用新方法,清晰又省力
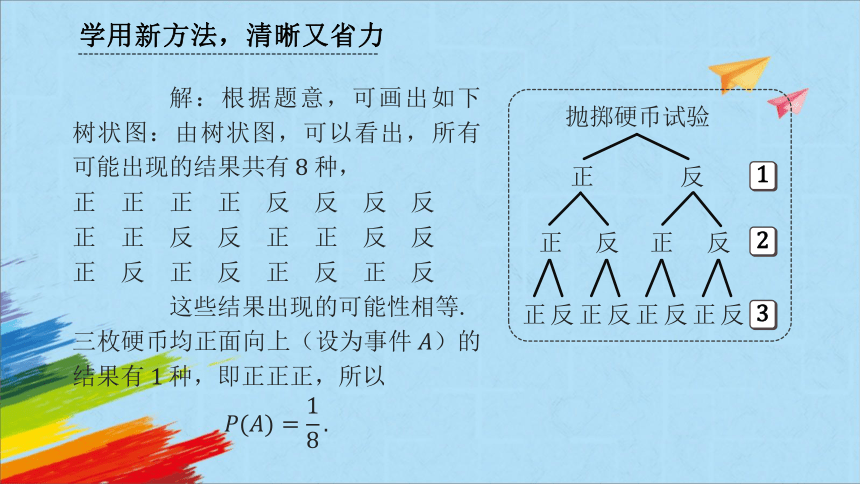
解:根据题意,可画出如下树状图:由树状图,可以看出,所有可能出现的结果共有种,
正 正 正 正 反 反 反 反
正 正 反 反 正 正 反 反
正 反 正 反 正 反 正 反
这些结果出现的可能性相等. 三枚硬币均正面向上(设为事件)的结果有种,即正正正,所以
抛掷硬币试验
正
反
正
反
正
反
正
反
正
反
正
反
正
反
1
2
3
知识小结
画树状图求等可能事件概率的一般步骤:
明确一次试验分几个步骤(有几个要素)及其顺序.
1
画树状图列举一次试验的所有可能结果.
2
数出等可能事件包含的结果数,及试验的所有可能结果数 .
3
用概率公式 进行计算.
4
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
我们要从三个口袋中,各随机取出一个球,也就是说这是一个三步试验,且每两步之间相互没有影响.
我们要确定每一步取出的结果数,有多少个?这些结果出现的可能性相等吗?
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
解:根据题意,可画出如下树状图:
根据树状图,可以看出,所有可能出现的结果是个,即
应用方法,巩固基础
解:根据题意,可画出如下树状图:
根据树状图,可以看出,所有可能出现的结果是个,即
这些结果出现的可能性相等,恰有一个元音字母的结果有个,所以 恰有一个元音字母
应用方法,巩固基础
顺序:乙-丙-甲,可画出如下树状图:
顺序:甲-丙-乙,可画出如下树状图:
乙
丙
甲
甲
丙
乙
应用方法,巩固基础
假定鸟卵孵化后,雏鸟为雌鸟与雄鸟的概率相同. 如果枚鸟卵全部成功孵化,那么只雏鸟中恰有只雄鸟的概率是多少?
练习
分析
关键是要列举只鸟的雌雄情况,所以我们可将此问题归结为一个三步试验,每一步可确定一只鸟的雌雄情况.
解:根据题意,可画出如下树状图:
第只鸟
第只鸟
第只鸟
雄
雄
雄
雄
雄
雄
由树状图,可以看出,所有可能出现的结果有 种. 且这些结果出现的可能性相等,
解:根据题意,可画出如下树状图:
由树状图,可以看出,所有可能出现的结果有 种. 且这些结果出现的可能性相等,
其中恰有两只雄鸟(记为事件)的结果有种,即(雌,雄,雄),(雄,雌,雄),(雄,雄,雌),
所以
第只鸟
第只鸟
第只鸟
雄
雄
雄
雄
雄
雄
合理归型,灵活运用
一个不透明的口袋中有四个完全相同的小球,把它们分别标号为依次随机摸出三个球,每摸出一个球都不再放回袋中,求其中两个球标号之和等于第三个球标号的概率是多少?
例2
分析
列举摸出的三个球标号情况,是该问题关键. 该试验可归结为三步试验,由于“不放回”,后一步受前一步操作影响,拿第一个球会有种等可能结果,第二个球就剩三种等可能结果,第三个球则只有两种等可能结果.
由树状图,可看出,所有可能出现的结果有种. 且这些结果出现的可能性相等,其中两个球标号之和等于第三个球标号(记为事件)的结果有 种,即
解:根据题意,可画出如下树状图:
所以
由树状图,可看出,所有可能出现的结果有种. 且这些结果出现的可能性相等,其中两个球标号之和等于第三个球标号(记为事件)的结果有 种,即
解:根据题意,可画出如下树状图:
所以
由树状图,可看出,所有可能出现的结果有种. 且这些结果出现的可能性相等,其中两个球标号之和等于第三个球标号(记为事件)的结果有 种,即
解:根据题意,可画出如下树状图:
所以
合理归型,灵活运用
从这四个数字中任取个数,可组成个无重复数字的三位数,若三位数的十位数字比个位和百位都大,则被称为“伞数”. 甲、乙两人玩游戏,将这个三位数依次写在个质地均匀小球上,规则是:从这个球中任取一球,若球上标着的三位数是“伞数”,则甲胜,否则乙胜.
练习
你认为这个游戏规则公平吗?
1
如果不公平,你能制定出一个公平的游戏规则吗?
2
合理归型,灵活运用
练习
你认为这个游戏规则公平吗?
如果不公平,你能制定出一个公平的游戏规则吗?
2
1
从这四个数字中任取个数,可组成个无重复数字的三位数,若三位数的十位数字比个位和百位都大,则被称为“伞数”. 甲、乙两人玩游戏,将这个三位数依次写在个质地均匀小球上,规则是:从这个球中任取一球,若球上标着的三位数是“伞数”,则甲胜,否则乙胜.
合理归型,灵活运用
练习
你认为这个游戏规则公平吗?
如果不公平,你能制定出一个公平的游戏规则吗?
2
1
从这四个数字中任取个数,可组成个无重复数字的三位数,若三位数的十位数字比个位和百位都大,则被称为“伞数”. 甲、乙两人玩游戏,将这个三位数依次写在个质地均匀小球上,规则是:从这个球中任取一球,若球上标着的三位数是“伞数”,则甲胜,否则乙胜.
合理归型,灵活运用
练习
你认为这个游戏规则公平吗?
1
如果不公平,你能制定出一个公平的游戏规则吗?
2
从这四个数字中任取个数,可组成个无重复数字的三位数,若三位数的十位数字比个位和百位都大,则被称为“伞数”. 甲、乙两人玩游戏,将这个三位数依次写在个质地均匀小球上,规则是:从这个球中任取一球,若球上标着的三位数是“伞数”,则甲胜,否则乙胜.
分析
怎样算公平?
1
组成的三位数共有哪些可能结果?是“伞数”的又有多少个?
2
要点分析
伞数:三位数的十位上数字最大.
从这个数中取个数字,组成无重复数字的位数,类似从标号为的 个球中不放回地取个球.
由树状图,可看出,所有可能出现的结果有 种. 且这些结果出现的可能性相等,其中是伞数(记为事件)的有种,即,,,,,,,,所以
解:根据题意,可画出如下树状图:
百位数
十位数
个位数
想一想:从四个数字中任选三个数字,取得任意三个数的可能性都是相等的?
思考
变整体思考为局部分析
围绕问题关键点进行分析
是伞数的关键在于,十位数字要最大. 因此我们将思考重点放在最大数可能出现的位置,可知总共有种等可能性的结果,即出现在百位、十位、个位. 是伞数则最大数只能出现在十位. 因此,整体来看,是伞数的概率也为 .
假如取出的三个数字为组成的三位数有种,即,,,,,,此时,是伞数的情况有和两种,因此局部来看,是伞数的概率为 ,若取出的是其他三个数字,局部来看是伞数的概率依然是 ,于是整个问题中,是伞数的概率也应该是 .
合理归型,灵活运用
显然,是伞数的概率仅有 ,因此乙更容易获胜,游戏规则不公平!
如何设计才能公平?你能发现例和该练习的区别和联系吗?
解:
2
将规则改为从 这四个数字中任取 个数组成
无重复数字的三位数. 如果任意两个位置上的数字之和等
于第三个位置上的数字,则甲胜,否则乙胜,则游戏公平.
合理归型,灵活运用
显然,是伞数的概率仅有 ,因此乙更容易获胜,游戏规则不公平!
如何设计才能公平?你能发现例和该练习的区别和联系吗?
解:
2
将规则改为从 这四个数字中任取 个数组成
无重复数字的三位数. 如果任意两个位置上的数字之和等
于第三个位置上的数字,则甲胜,否则乙胜,则游戏公平.
轻松一刻,活学活用
一个行李箱可设置位密码(每个位置上的数字可以是 这个数字中的一个). 请问任意拨 个数字,密码箱恰好能打开的概率是多少?
思考
分析
这依然是一个三步试验,但最终可能的结果数太多,可由前面列树状图经验,得知第一个位置的 种可能结果,对应第二个位置的个可能结果,配对方式有 种,这种再与第三个位置的种可能结果配对,则可组成组密码,而正确密码唯一.
答案:密码箱恰好能打开的概率为千分之一.
两只密码
箱的故事
请撬锁师傅来撬锁.
自己破密解锁.
有两个舍友,也许是他们当初设密码的时候出现了失误,也许是忘记了密码,密码箱都无法打开了.
密码箱变成了一只普通的储物箱.
十几分钟他就打开了密码箱 .
分析
每次尝试打开需要一秒,又需要一千秒,大约需要两千多秒;
最多四十分钟肯定能打开密码箱.
每拨一个数字大约需要一秒,一千组密码大约需要一千秒;
破密
撬锁
两只密码
箱的故事
课
堂
小
结
一、学会了用画树状图的方法求等可能事件概率
尤其适用于三步及三步以上试验列举结果.
明确要干什么事,分几步是关键.
画树状图的步骤.
清晰直观,易操作.
树状图
课
堂
小
结
二、知道了两个典型概率试验模型及其概率求法
可放回(可重复)
不放回(不可重复)
摸球试验
投掷硬币试验
典型模型
课
堂
小
结
三、认识到加强数学模型意识和数学应用意识的重要性
数学应用意识
数学模型意识
需增强
两个意识
课后作业
经过某十字路口的汽车,可能直行,也可能向左转或向右转. 如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
三辆车全部继续直行;
两辆车向右转,一辆车向左转;
至少有两辆车向左转.
1
2
3
课后作业
小红、小明、小军三人参加课外兴趣小组,他们都计划从编程小组、科技小组、书法小组中选择其中一个.
1
求三人选择同一个兴趣小组的概率;
2
求三人都选择不同兴趣小组的概率.
小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清,随便穿了两只就去上学,问小明正好穿的是同一双袜子的概率是多少?
课后作业
定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“数”,如“”就是一个“数”. 求下列事件的概率:
1
若十位上的数字为,则从中任选两数,能与 组成“数”;
2
从中任选三个数,能组成“数”.
(第二课时)
用列举法求概率
应用旧方法,解决新问题
分析
列表法已经难以胜任(表格是二维的,不便于加入第三枚硬币情况),还有什么方法列举结果呢?
引例
同时抛掷三枚质地均匀的硬币,你能求出三枚硬币均正面向上的概率吗?
应用旧方法,解决新问题
直接列举不重不漏的要点:有序,化多变为一变(先保证其他要素不变,只变其中一个要素)
引例
同时抛掷三枚质地均匀的硬币,你能求出三枚硬币均正面向上的概率吗?
正正正
正正反
正反正
正反反
反正正
反正反
反反正
反反反
应用旧方法,解决新问题
引例
同时抛掷三枚质地均匀的硬币,你能求出三枚硬币均正面向上的概率吗?
解:同时抛掷三枚硬币,所有可能的结果有种,即正正正,正正反,正反正,正反反,反正正,反正反,反反正,反反反. 其中,三枚硬币均正面向上(设为事件 )的结果仅有种,即正正正,所以
学用新方法,清晰又省力
分析
第一枚可能出现两种等可能结果:正、反(第一层),每一种结果又可与第二枚可能出现的正反两种等可能结果配对,因此,抛掷两枚硬币,会出现四种等可能结果(第二层),再抛第三枚,可能出现正、反两种结果,和第二层出现的四种结果配对,产生八种等可能结果(第三层). 由于这种表示方式像极了倒过来、不断分出枝杈的大树,所以我们叫它“树状图”.
抛掷硬币试验
正
反
正
反
正
反
正
反
正
反
正
反
正
反
1
2
3
学用新方法,清晰又省力
分析
第一枚可能出现两种等可能结果:正、反(第一层),每一种结果又可与第二枚可能出现的正反两种等可能结果配对,因此,抛掷两枚硬币,会出现四种等可能结果(第二层),再抛第三枚,可能出现正、反两种结果,和第二层出现的四种结果配对,产生八种等可能结果(第三层). 由于这种表示方式像极了倒过来、不断分出枝杈的大树,所以我们叫它“树状图”.
抛掷硬币试验
正
反
正
反
正
反
正
反
正
反
正
反
正
反
1
2
3
学用新方法,清晰又省力
分析
第一枚可能出现两种等可能结果:正、反(第一层),每一种结果又可与第二枚可能出现的正反两种等可能结果配对,因此,抛掷两枚硬币,会出现四种等可能结果(第二层),再抛第三枚,可能出现正、反两种结果,和第二层出现的四种结果配对,产生八种等可能结果(第三层). 由于这种表示方式像极了倒过来、不断分出枝杈的大树,所以我们叫它“树状图”.
抛掷硬币试验
正
反
正
反
正
反
正
反
正
反
正
反
正
反
1
2
3
学用新方法,清晰又省力
分析
第一枚可能出现两种等可能结果:正、反(第一层),每一种结果又可与第二枚可能出现的正反两种等可能结果配对,因此,抛掷两枚硬币,会出现四种等可能结果(第二层),再抛第三枚,可能出现正、反两种结果,和第二层出现的四种结果配对,产生八种等可能结果(第三层). 由于这种表示方式像极了倒过来、不断分出枝杈的大树,所以我们叫它“树状图”.
抛掷硬币试验
正
反
正
反
正
反
正
反
正
反
正
反
正
反
1
2
3
学用新方法,清晰又省力
分析
第一枚可能出现两种等可能结果:正、反(第一层),每一种结果又可与第二枚可能出现的正反两种等可能结果配对,因此,抛掷两枚硬币,会出现四种等可能结果(第二层),再抛第三枚,可能出现正、反两种结果,和第二层出现的四种结果配对,产生八种等可能结果(第三层). 由于这种表示方式像极了倒过来、不断分出枝杈的大树,所以我们叫它“树状图”.
抛掷硬币试验
正
反
正
反
正
反
正
反
正
反
正
反
正
反
1
2
3
学用新方法,清晰又省力
分析
第一枚可能出现两种等可能结果:正、反(第一层),每一种结果又可与第二枚可能出现的正反两种等可能结果配对,因此,抛掷两枚硬币,会出现四种等可能结果(第二层),再抛第三枚,可能出现正、反两种结果,和第二层出现的四种结果配对,产生八种等可能结果(第三层). 由于这种表示方式像极了倒过来、不断分出枝杈的大树,所以我们叫它“树状图”.
抛掷硬币试验
正
反
正
反
正
反
正
反
正
反
正
反
正
反
“树状图”
1
2
3
学用新方法,清晰又省力
解:根据题意,可画出如下树状图:由树状图,可以看出,所有可能出现的结果共有种,
正 正 正 正 反 反 反 反
正 正 反 反 正 正 反 反
正 反 正 反 正 反 正 反
这些结果出现的可能性相等. 三枚硬币均正面向上(设为事件)的结果有种,即正正正,所以
抛掷硬币试验
正
反
正
反
正
反
正
反
正
反
正
反
正
反
1
2
3
知识小结
画树状图求等可能事件概率的一般步骤:
明确一次试验分几个步骤(有几个要素)及其顺序.
1
画树状图列举一次试验的所有可能结果.
2
数出等可能事件包含的结果数,及试验的所有可能结果数 .
3
用概率公式 进行计算.
4
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
我们要从三个口袋中,各随机取出一个球,也就是说这是一个三步试验,且每两步之间相互没有影响.
我们要确定每一步取出的结果数,有多少个?这些结果出现的可能性相等吗?
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
甲口袋中装有个相同的小球,它们分别写有字母和;乙口袋中装有个相同的小球,它们分别写有字母和;丙口袋中装有个相同的小球,它们分别写有字母和. 从三个口袋中各随机取出个小球. 取出的个小球上恰好有个元音字母的概率是多少?(注:本题是元音字母)
例1
应用方法,巩固基础
解:根据题意,可画出如下树状图:
根据树状图,可以看出,所有可能出现的结果是个,即
应用方法,巩固基础
解:根据题意,可画出如下树状图:
根据树状图,可以看出,所有可能出现的结果是个,即
这些结果出现的可能性相等,恰有一个元音字母的结果有个,所以 恰有一个元音字母
应用方法,巩固基础
顺序:乙-丙-甲,可画出如下树状图:
顺序:甲-丙-乙,可画出如下树状图:
乙
丙
甲
甲
丙
乙
应用方法,巩固基础
假定鸟卵孵化后,雏鸟为雌鸟与雄鸟的概率相同. 如果枚鸟卵全部成功孵化,那么只雏鸟中恰有只雄鸟的概率是多少?
练习
分析
关键是要列举只鸟的雌雄情况,所以我们可将此问题归结为一个三步试验,每一步可确定一只鸟的雌雄情况.
解:根据题意,可画出如下树状图:
第只鸟
第只鸟
第只鸟
雄
雄
雄
雄
雄
雄
由树状图,可以看出,所有可能出现的结果有 种. 且这些结果出现的可能性相等,
解:根据题意,可画出如下树状图:
由树状图,可以看出,所有可能出现的结果有 种. 且这些结果出现的可能性相等,
其中恰有两只雄鸟(记为事件)的结果有种,即(雌,雄,雄),(雄,雌,雄),(雄,雄,雌),
所以
第只鸟
第只鸟
第只鸟
雄
雄
雄
雄
雄
雄
合理归型,灵活运用
一个不透明的口袋中有四个完全相同的小球,把它们分别标号为依次随机摸出三个球,每摸出一个球都不再放回袋中,求其中两个球标号之和等于第三个球标号的概率是多少?
例2
分析
列举摸出的三个球标号情况,是该问题关键. 该试验可归结为三步试验,由于“不放回”,后一步受前一步操作影响,拿第一个球会有种等可能结果,第二个球就剩三种等可能结果,第三个球则只有两种等可能结果.
由树状图,可看出,所有可能出现的结果有种. 且这些结果出现的可能性相等,其中两个球标号之和等于第三个球标号(记为事件)的结果有 种,即
解:根据题意,可画出如下树状图:
所以
由树状图,可看出,所有可能出现的结果有种. 且这些结果出现的可能性相等,其中两个球标号之和等于第三个球标号(记为事件)的结果有 种,即
解:根据题意,可画出如下树状图:
所以
由树状图,可看出,所有可能出现的结果有种. 且这些结果出现的可能性相等,其中两个球标号之和等于第三个球标号(记为事件)的结果有 种,即
解:根据题意,可画出如下树状图:
所以
合理归型,灵活运用
从这四个数字中任取个数,可组成个无重复数字的三位数,若三位数的十位数字比个位和百位都大,则被称为“伞数”. 甲、乙两人玩游戏,将这个三位数依次写在个质地均匀小球上,规则是:从这个球中任取一球,若球上标着的三位数是“伞数”,则甲胜,否则乙胜.
练习
你认为这个游戏规则公平吗?
1
如果不公平,你能制定出一个公平的游戏规则吗?
2
合理归型,灵活运用
练习
你认为这个游戏规则公平吗?
如果不公平,你能制定出一个公平的游戏规则吗?
2
1
从这四个数字中任取个数,可组成个无重复数字的三位数,若三位数的十位数字比个位和百位都大,则被称为“伞数”. 甲、乙两人玩游戏,将这个三位数依次写在个质地均匀小球上,规则是:从这个球中任取一球,若球上标着的三位数是“伞数”,则甲胜,否则乙胜.
合理归型,灵活运用
练习
你认为这个游戏规则公平吗?
如果不公平,你能制定出一个公平的游戏规则吗?
2
1
从这四个数字中任取个数,可组成个无重复数字的三位数,若三位数的十位数字比个位和百位都大,则被称为“伞数”. 甲、乙两人玩游戏,将这个三位数依次写在个质地均匀小球上,规则是:从这个球中任取一球,若球上标着的三位数是“伞数”,则甲胜,否则乙胜.
合理归型,灵活运用
练习
你认为这个游戏规则公平吗?
1
如果不公平,你能制定出一个公平的游戏规则吗?
2
从这四个数字中任取个数,可组成个无重复数字的三位数,若三位数的十位数字比个位和百位都大,则被称为“伞数”. 甲、乙两人玩游戏,将这个三位数依次写在个质地均匀小球上,规则是:从这个球中任取一球,若球上标着的三位数是“伞数”,则甲胜,否则乙胜.
分析
怎样算公平?
1
组成的三位数共有哪些可能结果?是“伞数”的又有多少个?
2
要点分析
伞数:三位数的十位上数字最大.
从这个数中取个数字,组成无重复数字的位数,类似从标号为的 个球中不放回地取个球.
由树状图,可看出,所有可能出现的结果有 种. 且这些结果出现的可能性相等,其中是伞数(记为事件)的有种,即,,,,,,,,所以
解:根据题意,可画出如下树状图:
百位数
十位数
个位数
想一想:从四个数字中任选三个数字,取得任意三个数的可能性都是相等的?
思考
变整体思考为局部分析
围绕问题关键点进行分析
是伞数的关键在于,十位数字要最大. 因此我们将思考重点放在最大数可能出现的位置,可知总共有种等可能性的结果,即出现在百位、十位、个位. 是伞数则最大数只能出现在十位. 因此,整体来看,是伞数的概率也为 .
假如取出的三个数字为组成的三位数有种,即,,,,,,此时,是伞数的情况有和两种,因此局部来看,是伞数的概率为 ,若取出的是其他三个数字,局部来看是伞数的概率依然是 ,于是整个问题中,是伞数的概率也应该是 .
合理归型,灵活运用
显然,是伞数的概率仅有 ,因此乙更容易获胜,游戏规则不公平!
如何设计才能公平?你能发现例和该练习的区别和联系吗?
解:
2
将规则改为从 这四个数字中任取 个数组成
无重复数字的三位数. 如果任意两个位置上的数字之和等
于第三个位置上的数字,则甲胜,否则乙胜,则游戏公平.
合理归型,灵活运用
显然,是伞数的概率仅有 ,因此乙更容易获胜,游戏规则不公平!
如何设计才能公平?你能发现例和该练习的区别和联系吗?
解:
2
将规则改为从 这四个数字中任取 个数组成
无重复数字的三位数. 如果任意两个位置上的数字之和等
于第三个位置上的数字,则甲胜,否则乙胜,则游戏公平.
轻松一刻,活学活用
一个行李箱可设置位密码(每个位置上的数字可以是 这个数字中的一个). 请问任意拨 个数字,密码箱恰好能打开的概率是多少?
思考
分析
这依然是一个三步试验,但最终可能的结果数太多,可由前面列树状图经验,得知第一个位置的 种可能结果,对应第二个位置的个可能结果,配对方式有 种,这种再与第三个位置的种可能结果配对,则可组成组密码,而正确密码唯一.
答案:密码箱恰好能打开的概率为千分之一.
两只密码
箱的故事
请撬锁师傅来撬锁.
自己破密解锁.
有两个舍友,也许是他们当初设密码的时候出现了失误,也许是忘记了密码,密码箱都无法打开了.
密码箱变成了一只普通的储物箱.
十几分钟他就打开了密码箱 .
分析
每次尝试打开需要一秒,又需要一千秒,大约需要两千多秒;
最多四十分钟肯定能打开密码箱.
每拨一个数字大约需要一秒,一千组密码大约需要一千秒;
破密
撬锁
两只密码
箱的故事
课
堂
小
结
一、学会了用画树状图的方法求等可能事件概率
尤其适用于三步及三步以上试验列举结果.
明确要干什么事,分几步是关键.
画树状图的步骤.
清晰直观,易操作.
树状图
课
堂
小
结
二、知道了两个典型概率试验模型及其概率求法
可放回(可重复)
不放回(不可重复)
摸球试验
投掷硬币试验
典型模型
课
堂
小
结
三、认识到加强数学模型意识和数学应用意识的重要性
数学应用意识
数学模型意识
需增强
两个意识
课后作业
经过某十字路口的汽车,可能直行,也可能向左转或向右转. 如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
三辆车全部继续直行;
两辆车向右转,一辆车向左转;
至少有两辆车向左转.
1
2
3
课后作业
小红、小明、小军三人参加课外兴趣小组,他们都计划从编程小组、科技小组、书法小组中选择其中一个.
1
求三人选择同一个兴趣小组的概率;
2
求三人都选择不同兴趣小组的概率.
小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清,随便穿了两只就去上学,问小明正好穿的是同一双袜子的概率是多少?
课后作业
定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“数”,如“”就是一个“数”. 求下列事件的概率:
1
若十位上的数字为,则从中任选两数,能与 组成“数”;
2
从中任选三个数,能组成“数”.
同课章节目录
