人教版九年级数学上册24.3正多边形和圆 第1课时教学课件(共29张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.3正多边形和圆 第1课时教学课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 22:54:24 | ||
图片预览




文档简介
(共29张PPT)
(第一课时)
正多边形和圆
复习回顾
正多边形:各边相等、各角也相等的多边形. 比如等边三角形、正方形等.
复习回顾
当边数为偶数时,正多边形也是中心对称图形;
复习回顾
正多边形是轴对称图形;
圆既是轴对称图形又是旋转对称图形.
正多边形和圆的关系联系非常密切,只要把一个圆分成相等的一些弧,就可以作出正多边形.
探究新知
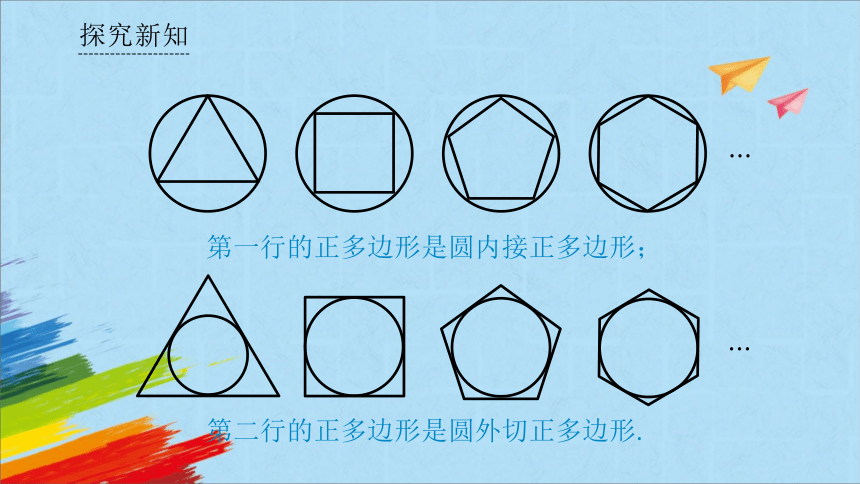
第一行的正多边形是圆内接正多边形;
第二行的正多边形是圆外切正多边形.
探究新知
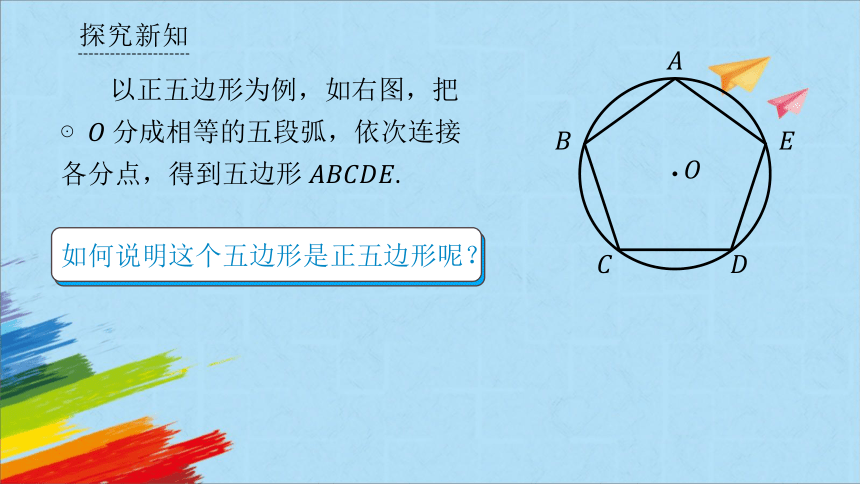
以正五边形为例,如右图,把⊙ 分成相等的五段弧,依次连接各分点,得到五边形.
如何说明这个五边形是正五边形呢?
探究新知
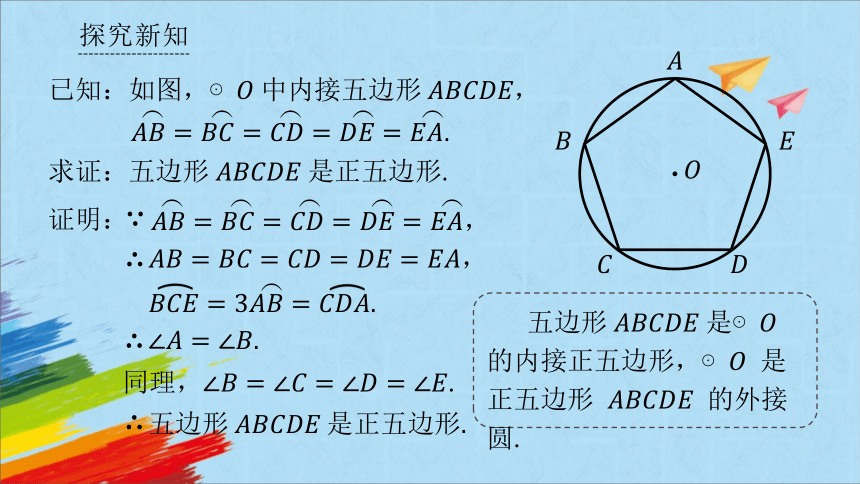
已知:如图,⊙ 中内接五边形,.
求证:五边形 是正五边形.
证明:
,
同理,.
五边形是⊙ 的内接正五边形,⊙ 是正五边形 的外接圆.
探究新知
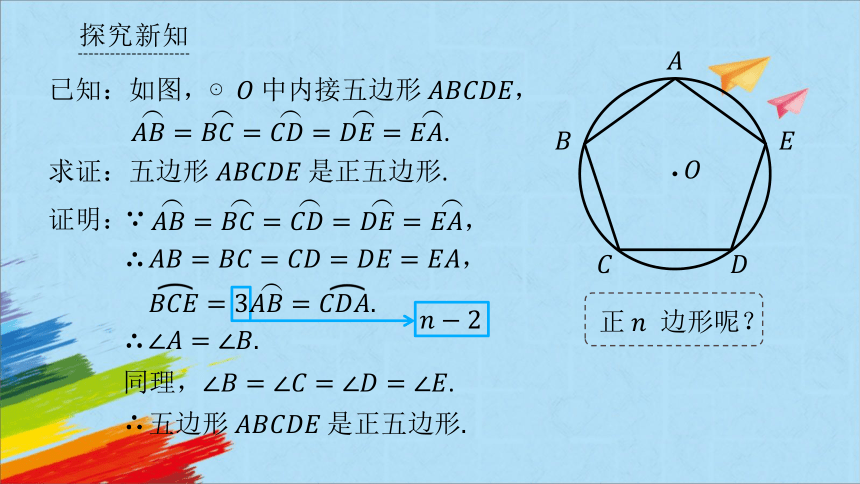
求证:五边形 是正五边形.
证明:
,
同理,.
正 边形呢?
已知:如图,⊙ 中内接五边形,.
外接圆的圆心叫做正多边形的中心,外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形一边的距离叫做正多边形的边心距.
外接圆的圆心叫做正多边形的中心,外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形一边的距离叫做正多边形的边心距.
外接圆的圆心叫做正多边形的中心,外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形一边的距离叫做正多边形的边心距.
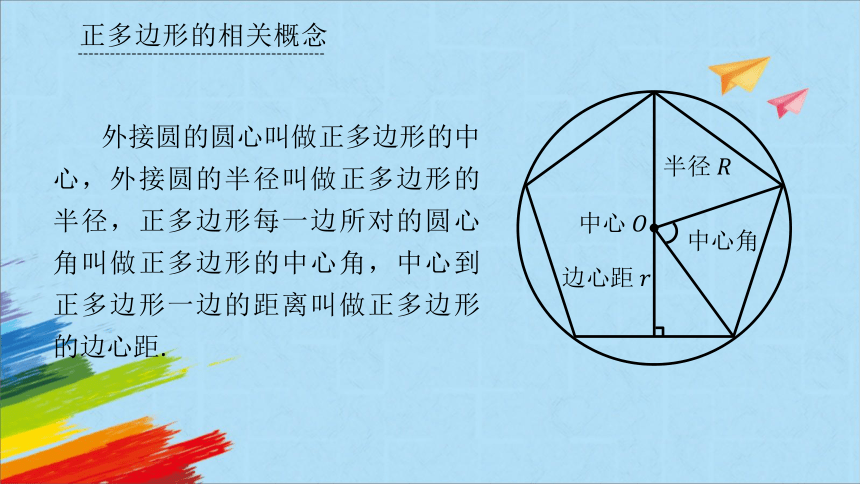
正多边形的相关概念
外接圆的圆心叫做正多边形的中心,外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形一边的距离叫做正多边形的边心距.
边心距
巩固运用
找出下列正多边形的中心,并标出正多边形的半径,边心距,中心角.
边心距
边心距
边心距
如图,矩形的四个角相等,但是四条边不相等,所以不是正多边形.
反例:
思考
各边相等的多边形是正多边形吗?
如图,菱形的四条边相等,但是四个角不相等,所以不是正多边形.
各角相等的多边形是正多边形吗?
反例:
思考
各边相等的圆内接多边形是正多边形吗?
以四边形为例
已知:如图,⊙ 中内接四边形 ,.
求证:四边形是正方形.
思考
已知:如图,⊙ 中内接四边形 ,.
求证:四边形是正方形.
证明:
,
.
同理,.
.
思考
各角相等的圆内接多边形是正多边形吗?
以四边形为例
如图,⊙ 中内接矩形 ,.
反例:矩形.
各角相等的圆内接多边形不一定是正多边形.
例题分析
若正三角形的半径为,则边长为 ,
1
分析
边心距为 ,面积为 .
例题分析
若正三角形的边长为,则半径为 .
1
.
分析
例题分析
要用圆形铁片截出边长为 的正方形铁片,选用的圆形铁片的半径至少是多少
2
分析
例题分析
如图,有一个亭子,它的地基是半径为 的正六边形,求地基的周长和面积(结果保留小数点后一位).
3
例题分析
如图,⊙中内接正六边形 半径为. 求正六边形 的周长和面积.
例题分析
解:连接 过点 作 于点.
.
推广思考
正边形的中心角度数如何计算?
正边形的一个外角度数如何计算?
正 边形的中心角和一个外角的度数相等.
推广思考
正边形的 条半径、 条边心距将正 边形分割成全等直角三角形的个数是多少?
如图,正六边形能分成个全等的直角三角形,则正 边形能分成 个全等的直角三角形.
每个直角三角形都由正多边形的哪些元素组成?
每个直角三角形都由正多边形的半径,边心距,边长一半组成.
阅读与思考
圆周率 是怎么算出来的?
阅读与思考
我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形来确定圆周率. 并指出圆的内接正多边形边数加倍的过程中“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣.”他计算出
拓广探索
把圆分成 等份,经过各分点作圆的切线,以相邻切线的交点为顶点的多边形叫做这个圆的外切正边形.
巩固练习
如图,若等边△ 的半径为 ,则边长为 ,内切圆的半径 为 .
分析
课
堂
小
结
1
2
在解决正多边形有关计算时,通过作正 边形的半径和边心距,把正 边形分为 个全等的直角三角形,再利用勾股定理,即可完成一些特殊的正多边形的计算.
3
课后作业
完成下表中有关正多边形的计算.
1
正多边形边数 内角 中心角 半径 边长 边心距 周长 面积
课后作业
用 长的篱笆在空地上围成一个绿化场地,现有四种设计方案:正三角形、正方形、正六边形、圆. 哪种场地的面积最大?
2
(第一课时)
正多边形和圆
复习回顾
正多边形:各边相等、各角也相等的多边形. 比如等边三角形、正方形等.
复习回顾
当边数为偶数时,正多边形也是中心对称图形;
复习回顾
正多边形是轴对称图形;
圆既是轴对称图形又是旋转对称图形.
正多边形和圆的关系联系非常密切,只要把一个圆分成相等的一些弧,就可以作出正多边形.
探究新知
第一行的正多边形是圆内接正多边形;
第二行的正多边形是圆外切正多边形.
探究新知
以正五边形为例,如右图,把⊙ 分成相等的五段弧,依次连接各分点,得到五边形.
如何说明这个五边形是正五边形呢?
探究新知
已知:如图,⊙ 中内接五边形,.
求证:五边形 是正五边形.
证明:
,
同理,.
五边形是⊙ 的内接正五边形,⊙ 是正五边形 的外接圆.
探究新知
求证:五边形 是正五边形.
证明:
,
同理,.
正 边形呢?
已知:如图,⊙ 中内接五边形,.
外接圆的圆心叫做正多边形的中心,外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形一边的距离叫做正多边形的边心距.
外接圆的圆心叫做正多边形的中心,外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形一边的距离叫做正多边形的边心距.
外接圆的圆心叫做正多边形的中心,外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形一边的距离叫做正多边形的边心距.
正多边形的相关概念
外接圆的圆心叫做正多边形的中心,外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形一边的距离叫做正多边形的边心距.
边心距
巩固运用
找出下列正多边形的中心,并标出正多边形的半径,边心距,中心角.
边心距
边心距
边心距
如图,矩形的四个角相等,但是四条边不相等,所以不是正多边形.
反例:
思考
各边相等的多边形是正多边形吗?
如图,菱形的四条边相等,但是四个角不相等,所以不是正多边形.
各角相等的多边形是正多边形吗?
反例:
思考
各边相等的圆内接多边形是正多边形吗?
以四边形为例
已知:如图,⊙ 中内接四边形 ,.
求证:四边形是正方形.
思考
已知:如图,⊙ 中内接四边形 ,.
求证:四边形是正方形.
证明:
,
.
同理,.
.
思考
各角相等的圆内接多边形是正多边形吗?
以四边形为例
如图,⊙ 中内接矩形 ,.
反例:矩形.
各角相等的圆内接多边形不一定是正多边形.
例题分析
若正三角形的半径为,则边长为 ,
1
分析
边心距为 ,面积为 .
例题分析
若正三角形的边长为,则半径为 .
1
.
分析
例题分析
要用圆形铁片截出边长为 的正方形铁片,选用的圆形铁片的半径至少是多少
2
分析
例题分析
如图,有一个亭子,它的地基是半径为 的正六边形,求地基的周长和面积(结果保留小数点后一位).
3
例题分析
如图,⊙中内接正六边形 半径为. 求正六边形 的周长和面积.
例题分析
解:连接 过点 作 于点.
.
推广思考
正边形的中心角度数如何计算?
正边形的一个外角度数如何计算?
正 边形的中心角和一个外角的度数相等.
推广思考
正边形的 条半径、 条边心距将正 边形分割成全等直角三角形的个数是多少?
如图,正六边形能分成个全等的直角三角形,则正 边形能分成 个全等的直角三角形.
每个直角三角形都由正多边形的哪些元素组成?
每个直角三角形都由正多边形的半径,边心距,边长一半组成.
阅读与思考
圆周率 是怎么算出来的?
阅读与思考
我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形来确定圆周率. 并指出圆的内接正多边形边数加倍的过程中“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣.”他计算出
拓广探索
把圆分成 等份,经过各分点作圆的切线,以相邻切线的交点为顶点的多边形叫做这个圆的外切正边形.
巩固练习
如图,若等边△ 的半径为 ,则边长为 ,内切圆的半径 为 .
分析
课
堂
小
结
1
2
在解决正多边形有关计算时,通过作正 边形的半径和边心距,把正 边形分为 个全等的直角三角形,再利用勾股定理,即可完成一些特殊的正多边形的计算.
3
课后作业
完成下表中有关正多边形的计算.
1
正多边形边数 内角 中心角 半径 边长 边心距 周长 面积
课后作业
用 长的篱笆在空地上围成一个绿化场地,现有四种设计方案:正三角形、正方形、正六边形、圆. 哪种场地的面积最大?
2
同课章节目录
