人教版九年级数学上册24.1.4圆周角 第1课时教学课件(共129张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.1.4圆周角 第1课时教学课件(共129张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 22:55:23 | ||
图片预览


文档简介
(共129张PPT)
圆周角
(第一课时)
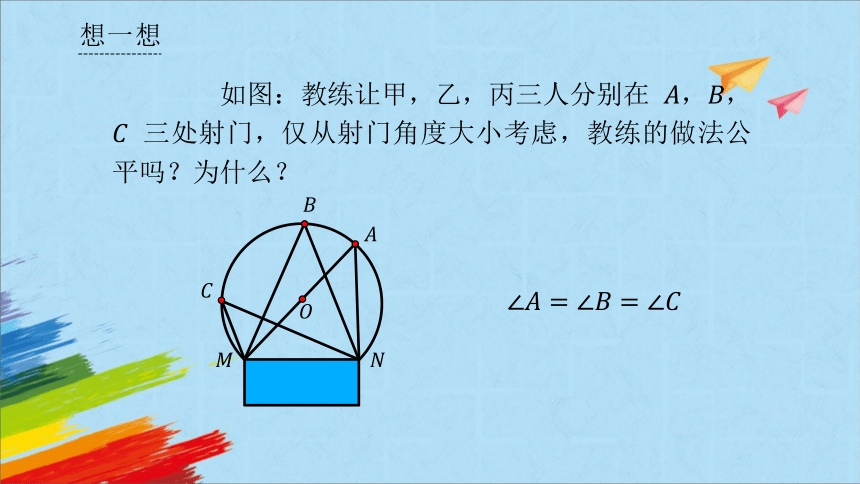
想一想
如图:教练让甲,乙,丙三人分别在 ,, 三处射门,仅从射门角度大小考虑,教练的做法公平吗?为什么?
复习
圆心角的概念
为⊙ 的圆心角,
圆心角:我们把顶点在圆心的角叫做圆心角.
所对的弦为 ,
所对的弧为 .
AB
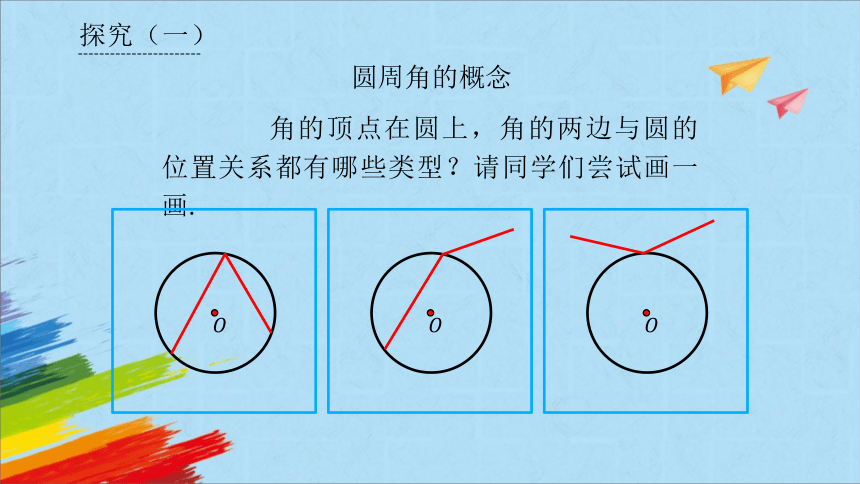
探究(一)
圆周角的概念
角的顶点在圆上,角的两边与圆的位置关系都有哪些类型?请同学们尝试画一画.
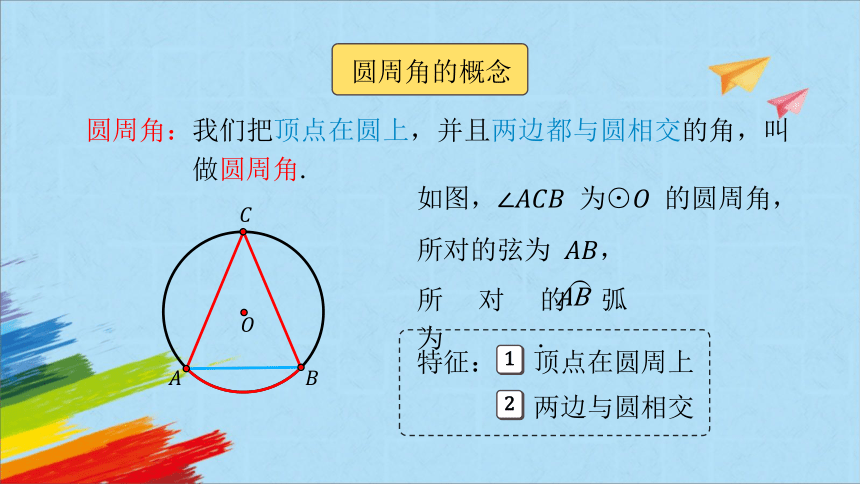
圆周角的概念
圆周角:
我们把顶点在圆上,并且两边都与圆相交的角,叫做圆周角.
如图, 为⊙ 的圆周角,
所对的弦为 ,
所对的弧为 .
AB
特征:
1
顶点在圆周上
2
两边与圆相交
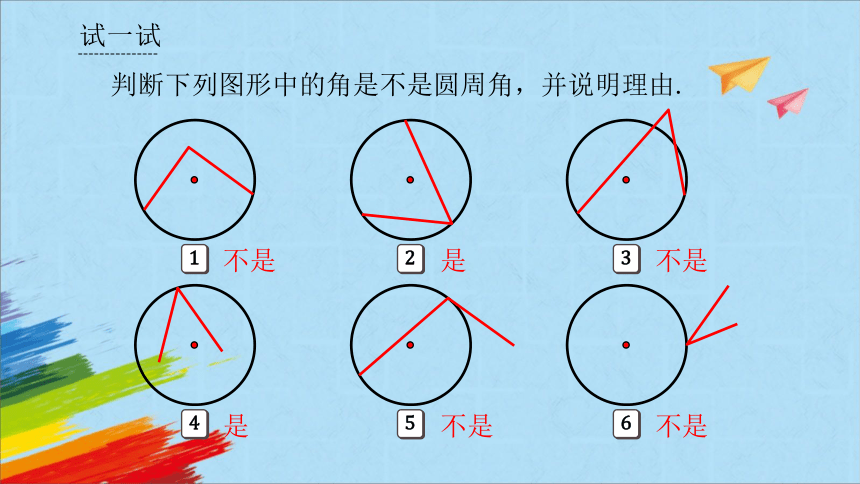
试一试
判断下列图形中的角是不是圆周角,并说明理由.
1
2
3
4
5
6
不是
是
不是
不是
不是
是
探究(二)
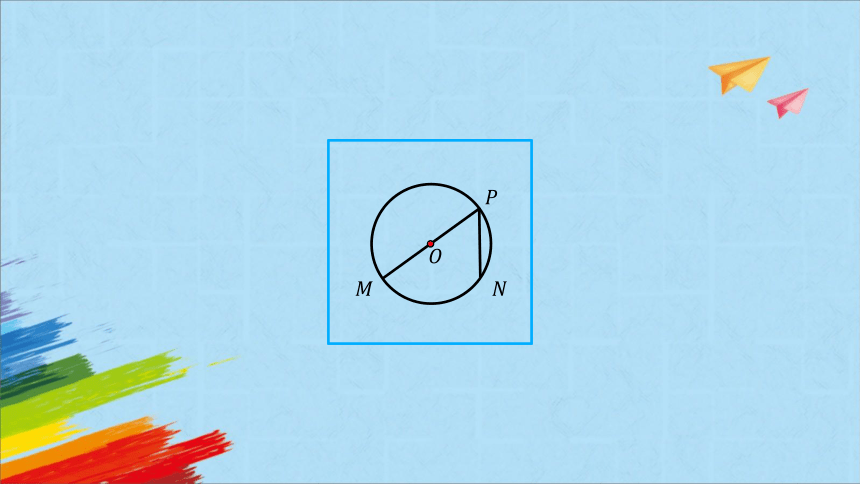
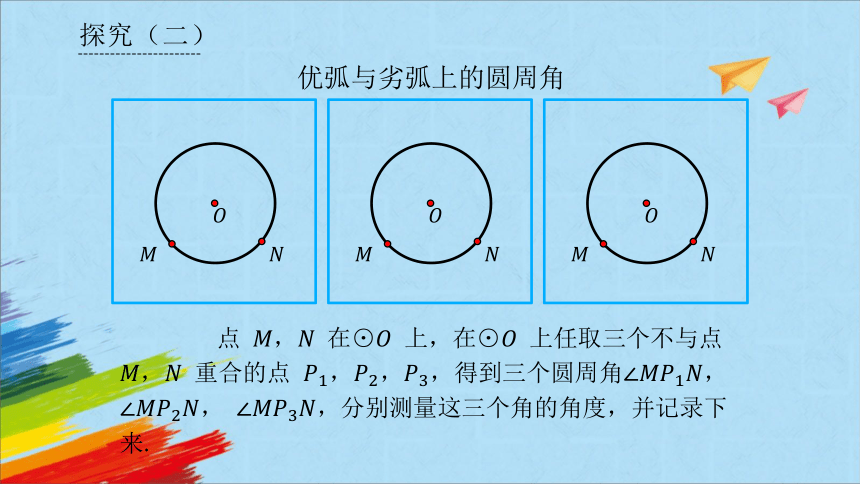
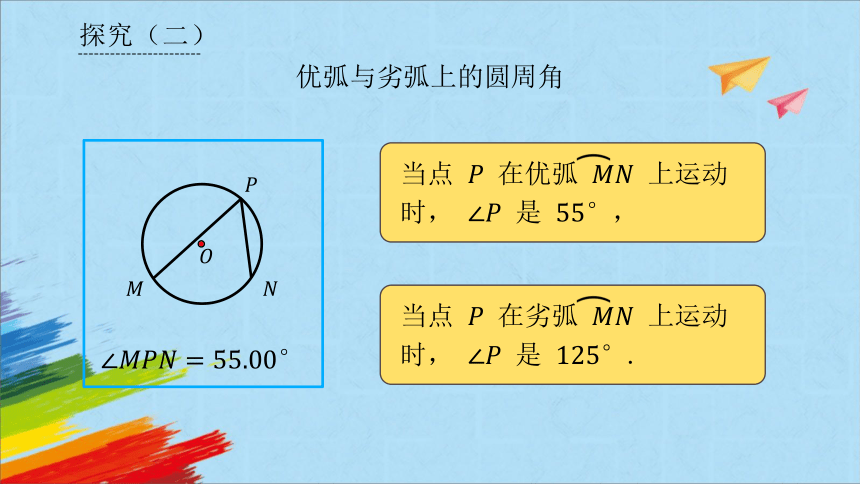
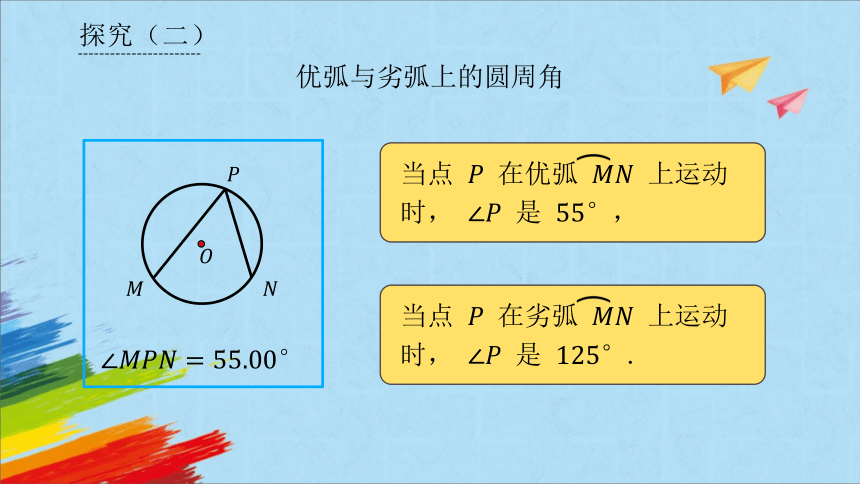
优弧与劣弧上的圆周角
点 , 在⊙ 上,在⊙ 上任取三个不与点 , 重合的点 ,,,得到三个圆周角, , ,分别测量这三个角的角度,并记录下来.
探究(二)
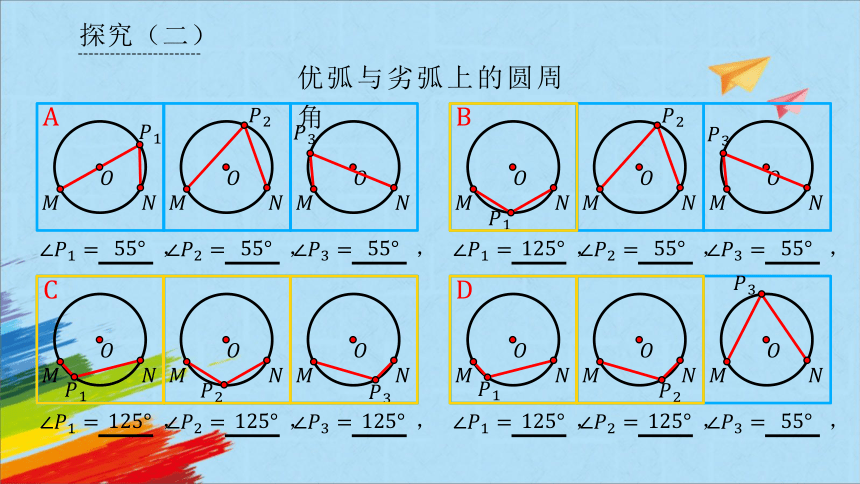
优弧与劣弧上的圆周角
,
,
,
,
,
,
,
,
,
,
,
,
探究(二)
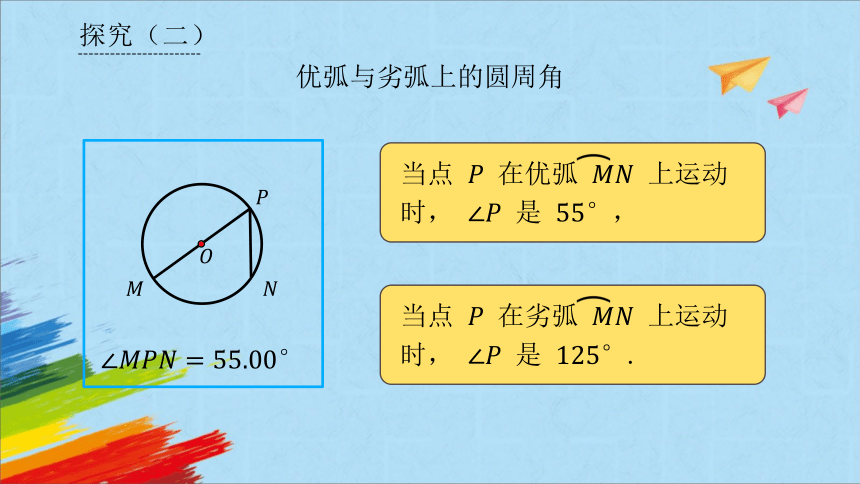
优弧与劣弧上的圆周角
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(三)
圆周角与圆心的位置关系
当点 在优弧 上运动时,将圆心 与 的边会出现的位置关系,画在上图中.
探究(三)
圆周角与圆心的位置关系
探究(三)
圆周角与圆心的位置关系
探究(三)
圆周角与圆心的位置关系
探究(三)
圆周角与圆心的位置关系
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
圆心在
圆周角的一边上
圆心在圆周角内
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(四)
圆周角与圆心的位置关系:.圆心在圆周角的一边上
,
.
又 是 的外角,
,
,
探究(四)
圆周角与圆心的位置关系:.圆心在圆周角内
连接 并延长,交⊙ 于点 .
探究(四)
圆周角与圆心的位置关系:.圆心在圆周角外
连接 并延长,交⊙ 于点 .
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
如图, 是 所对的圆周角, 是 所对的圆心角.
是 所对的圆周角,
如图,, 是 所对的圆周角,则 .
证明:
连接 ,.
是 所对的圆心角,
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
同弧所对的圆周角相等.
如图,,, 是 所对的圆周角,
.
探究(五)
圆周角与弧的关系
等弧所对的圆周角相等?
已知:如图, 与 相等,点 , 在⊙ 上,
证明:
求证:
连接 ,,,.
等弧所对的圆周角相等.
.
,
圆周角定理推论(一)
同弧或等弧所对的圆周角相等.
探究(六)
特殊的角度
在左图⊙ 上画出一条直径 ,及其所对的圆周角,并测量 的角度.
为 直径,
.
,
.
在右图 上画出个以点 为顶点的圆周角,使,再画出它所对的圆心角,并测量 的角度.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
是⊙ 直径,点 在⊙ 上,
圆心角是平角,弦是直径.
圆周角是直角,
圆周角定理推论(二)
半圆(或直径)所对的圆周角是直角.
圆周角定理推论(二)
的圆周角所对的弦是直径.
是⊙ 直径.
圆周角,
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
试一试
图
图
如图 ,已知 是⊙ 的直径,点 在⊙ 上,若,则.
1
如图 , 的顶点都在⊙ 上, 是⊙ 直径,若,则.
2
例
如图, ⊙ 的直径 为 ,弦 为 , 的平分线交⊙ 于点 ,求 ,, 的长.
.
解:
连接 ,.
是⊙ 的直径,, 在⊙ 上,
.
在 △ 中,
例
如图, ⊙ 的直径 为 ,弦 为 , 的平分线交⊙ 于点 ,求 ,, 的长.
平分,
.
又 在 △ 中, ,
,,
.
.
课
堂
小
结
圆周角,圆心角与弧之间的关系
1
一条弧所对的圆周角等于它所对的圆心角的一半.
课
堂
小
结
圆周角,圆心角与弧之间的关系
1
同弧或等弧所对的圆周角相等.
课
堂
小
结
直径与直角之间的关系
2
半圆(或直径)所对的圆周角是直角,
圆心角是平角,弦是直径.
圆周角是直角,
的圆周角所对的弦是直径.
课后作业
求证: .
如图,,, 都是⊙ 的半径,.
1
课后作业
如图,你能用三角尺确定一张圆形纸片的圆心吗?有几种方法?与同学交流一下.
2
课后作业
提高题:如图,圆上分布着 个点,,,,,从 起顺次连接 ,,,,,,,得到“七角星”,则 .
3
圆周角
(第一课时)
想一想
如图:教练让甲,乙,丙三人分别在 ,, 三处射门,仅从射门角度大小考虑,教练的做法公平吗?为什么?
复习
圆心角的概念
为⊙ 的圆心角,
圆心角:我们把顶点在圆心的角叫做圆心角.
所对的弦为 ,
所对的弧为 .
AB
探究(一)
圆周角的概念
角的顶点在圆上,角的两边与圆的位置关系都有哪些类型?请同学们尝试画一画.
圆周角的概念
圆周角:
我们把顶点在圆上,并且两边都与圆相交的角,叫做圆周角.
如图, 为⊙ 的圆周角,
所对的弦为 ,
所对的弧为 .
AB
特征:
1
顶点在圆周上
2
两边与圆相交
试一试
判断下列图形中的角是不是圆周角,并说明理由.
1
2
3
4
5
6
不是
是
不是
不是
不是
是
探究(二)
优弧与劣弧上的圆周角
点 , 在⊙ 上,在⊙ 上任取三个不与点 , 重合的点 ,,,得到三个圆周角, , ,分别测量这三个角的角度,并记录下来.
探究(二)
优弧与劣弧上的圆周角
,
,
,
,
,
,
,
,
,
,
,
,
探究(二)
优弧与劣弧上的圆周角
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(二)
当点 在优弧 上运动时, 是 ,
当点 在劣弧 上运动时, 是 .
优弧与劣弧上的圆周角
探究(三)
圆周角与圆心的位置关系
当点 在优弧 上运动时,将圆心 与 的边会出现的位置关系,画在上图中.
探究(三)
圆周角与圆心的位置关系
探究(三)
圆周角与圆心的位置关系
探究(三)
圆周角与圆心的位置关系
探究(三)
圆周角与圆心的位置关系
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角外
圆心在
圆周角的一边上
圆心在圆周角内
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(三)
圆周角与圆心的位置关系
圆心在圆周角内
圆心在圆周角外
圆心在
圆周角的一边上
探究(四)
圆周角与圆心的位置关系:.圆心在圆周角的一边上
,
.
又 是 的外角,
,
,
探究(四)
圆周角与圆心的位置关系:.圆心在圆周角内
连接 并延长,交⊙ 于点 .
探究(四)
圆周角与圆心的位置关系:.圆心在圆周角外
连接 并延长,交⊙ 于点 .
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
如图, 是 所对的圆周角, 是 所对的圆心角.
是 所对的圆周角,
如图,, 是 所对的圆周角,则 .
证明:
连接 ,.
是 所对的圆心角,
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
探究(五)
圆周角与弧的关系
同弧所对的圆周角相等.
如图,,, 是 所对的圆周角,
.
探究(五)
圆周角与弧的关系
等弧所对的圆周角相等?
已知:如图, 与 相等,点 , 在⊙ 上,
证明:
求证:
连接 ,,,.
等弧所对的圆周角相等.
.
,
圆周角定理推论(一)
同弧或等弧所对的圆周角相等.
探究(六)
特殊的角度
在左图⊙ 上画出一条直径 ,及其所对的圆周角,并测量 的角度.
为 直径,
.
,
.
在右图 上画出个以点 为顶点的圆周角,使,再画出它所对的圆心角,并测量 的角度.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
探究(六)
特殊的角度
为 直径,
.
,
.
是⊙ 直径,点 在⊙ 上,
圆心角是平角,弦是直径.
圆周角是直角,
圆周角定理推论(二)
半圆(或直径)所对的圆周角是直角.
圆周角定理推论(二)
的圆周角所对的弦是直径.
是⊙ 直径.
圆周角,
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
探究(六)
特殊的角度
试一试
图
图
如图 ,已知 是⊙ 的直径,点 在⊙ 上,若,则.
1
如图 , 的顶点都在⊙ 上, 是⊙ 直径,若,则.
2
例
如图, ⊙ 的直径 为 ,弦 为 , 的平分线交⊙ 于点 ,求 ,, 的长.
.
解:
连接 ,.
是⊙ 的直径,, 在⊙ 上,
.
在 △ 中,
例
如图, ⊙ 的直径 为 ,弦 为 , 的平分线交⊙ 于点 ,求 ,, 的长.
平分,
.
又 在 △ 中, ,
,,
.
.
课
堂
小
结
圆周角,圆心角与弧之间的关系
1
一条弧所对的圆周角等于它所对的圆心角的一半.
课
堂
小
结
圆周角,圆心角与弧之间的关系
1
同弧或等弧所对的圆周角相等.
课
堂
小
结
直径与直角之间的关系
2
半圆(或直径)所对的圆周角是直角,
圆心角是平角,弦是直径.
圆周角是直角,
的圆周角所对的弦是直径.
课后作业
求证: .
如图,,, 都是⊙ 的半径,.
1
课后作业
如图,你能用三角尺确定一张圆形纸片的圆心吗?有几种方法?与同学交流一下.
2
课后作业
提高题:如图,圆上分布着 个点,,,,,从 起顺次连接 ,,,,,,,得到“七角星”,则 .
3
同课章节目录
