人教版九年级数学上册《正多边形和圆》第2课时教学课件 (共28张PPT)
文档属性
| 名称 | 人教版九年级数学上册《正多边形和圆》第2课时教学课件 (共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 06:56:56 | ||
图片预览



文档简介
(共28张PPT)
(第二课时)
正多边形和圆
情境引入
实际生活中,经常遇到画正多边形的问题,比如画一个六角螺帽的平面图,画一个五角星等,这些问题都与等分圆周有关. 要制造如下图中的零件,也需要等分圆周.
引入新知
已知⊙的半径为 ,画圆的内接正三角形.
探究新知
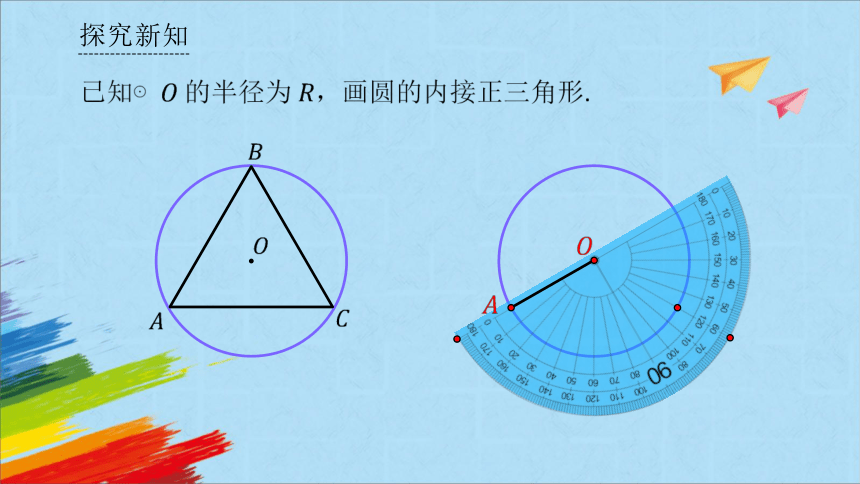
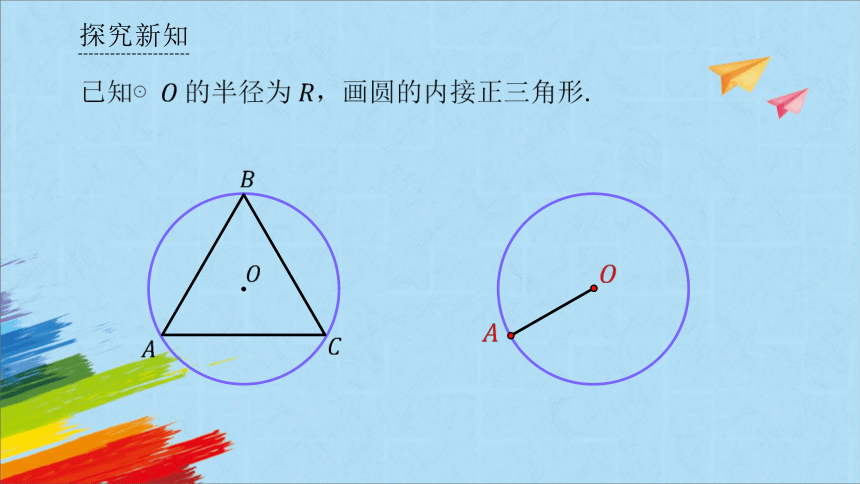
已知⊙的半径为 ,画圆的内接正三角形.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
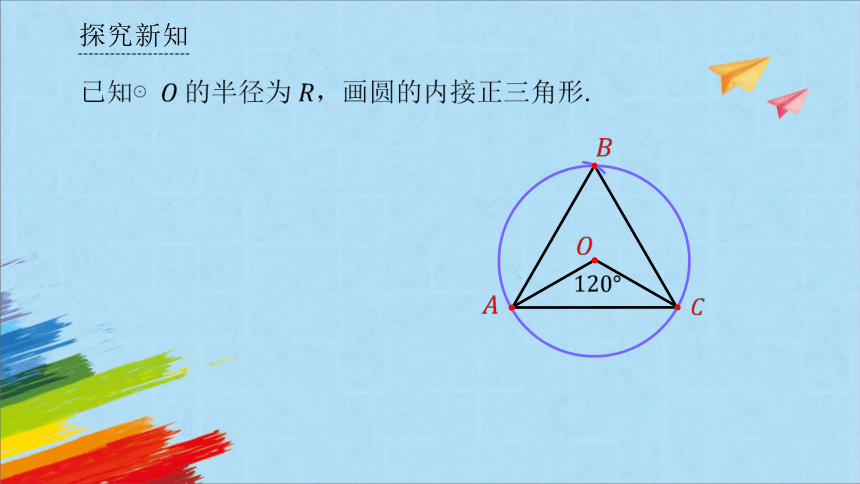
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
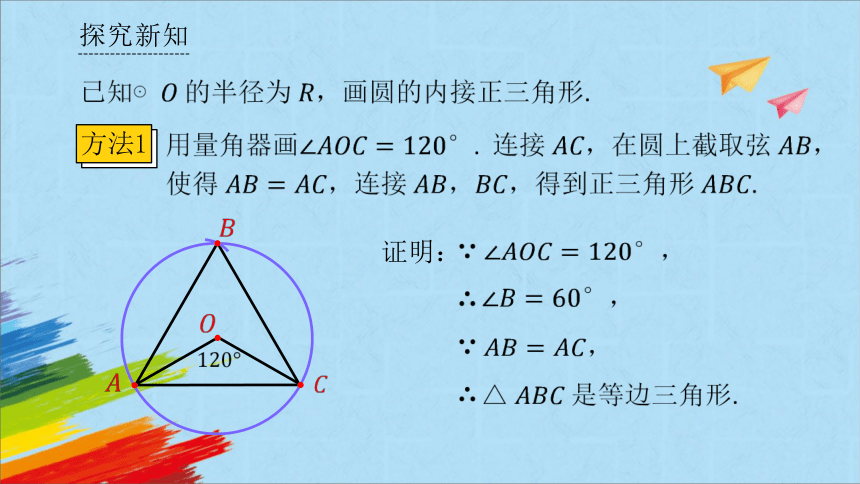
方法1
用量角器画. 连接在圆上截取弦,使得 ,连接得到正三角形.
证明:
,
.
,
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
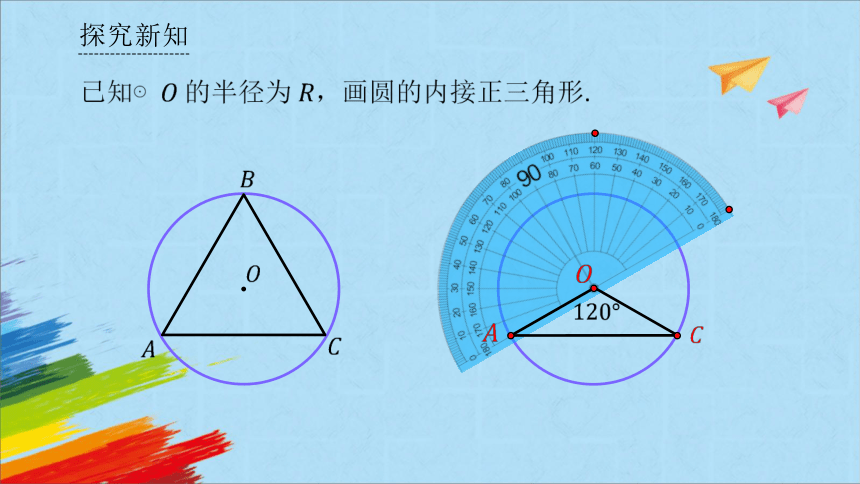
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
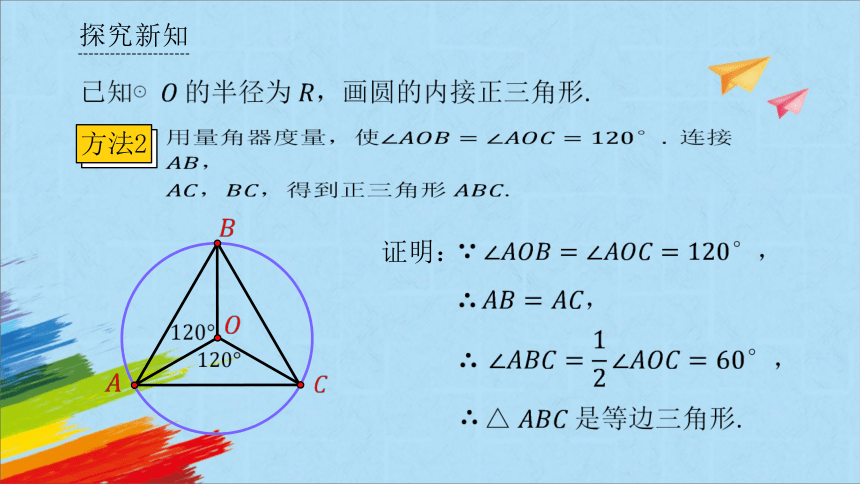
方法2
用量角器度量,使 连接
得到正三角形 .
证明:
,
.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
方法3
用量角器度量,使
证明:
,
平分,
,
.
点在所在的直线上,
,
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
方法4
用圆规在⊙ 上顺次截取两条长度等于 的弦,连接其中的 即可. 得到正三角形.
分析
.
.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
方法5
用圆规在⊙ 上顺次截取 条长度等于半径 的弦,连接其中的 即可. 得到正三角形.
分析
,
,
.
拓广思考
如何作出圆内接正方形呢?
拓广思考
还可以怎么作正六边形和正方形呢?
拓广思考
类比,如何作出圆内接正八边形呢
拓广思考
还可以用什么方法作出圆内接正八边形 ?
拓广思考
你还可以用什么方法作出圆内接八边形吗?
拓广思考
照此方法依次可作正十六边形、正三十二边形、正六十四边形
方法总结
先用量角器画一个中心角,然后在圆上依次截取等于该中心角所对弧的等弧,于是得到圆的等分点,相对比较简单,但画图的误差积累到最后一个等分点,误差较大.
2
尺规作图,虽然精确,但不是任意等分圆周都能用这种方法,而且作图时存在误差.
3
1
依次画出相等的中心角来等分圆. 比较准确,但是麻烦. 由于限制条件少,可以作为画圆内接正多边形的通法.
本节课提到的其他一些方法只适用于某些特殊的正多边形.
4
练习
如何在半径为 的⊙ 中作出内接正九边形呢?
1
练习
如何借助圆画出一个五角星呢?
2
练习
用等分圆的方法画出下列图案.
3
欣赏图片
用等分圆的方法可以画出如下美丽的图案,欣赏一下.
课
堂
小
结
利用等分圆的方法我们可以画出正多边形.
1
对于一些特殊的正多边形比如正六边形,正方形等可以使用尺规作图的方法来作图.
2
借助圆和正多边形也可以设计一些美丽的图案.
3
通用的方法:用量角器等分圆.
依次画出相等的中心角来等分圆.
先用量角器画一个中心角,然后在圆上依次截取等于该中心角所对弧的等弧来等分圆.
课后作业
尝试用不同的方法画一个正六边形.
1
用等分圆的方法画出下列图案,并给它们涂上你喜欢的颜色.
2
尝试用等分圆周的方法设计一些美丽的图案.
3
(第二课时)
正多边形和圆
情境引入
实际生活中,经常遇到画正多边形的问题,比如画一个六角螺帽的平面图,画一个五角星等,这些问题都与等分圆周有关. 要制造如下图中的零件,也需要等分圆周.
引入新知
已知⊙的半径为 ,画圆的内接正三角形.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
方法1
用量角器画. 连接在圆上截取弦,使得 ,连接得到正三角形.
证明:
,
.
,
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
方法2
用量角器度量,使 连接
得到正三角形 .
证明:
,
.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
方法3
用量角器度量,使
证明:
,
平分,
,
.
点在所在的直线上,
,
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
方法4
用圆规在⊙ 上顺次截取两条长度等于 的弦,连接其中的 即可. 得到正三角形.
分析
.
.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
探究新知
已知⊙的半径为 ,画圆的内接正三角形.
方法5
用圆规在⊙ 上顺次截取 条长度等于半径 的弦,连接其中的 即可. 得到正三角形.
分析
,
,
.
拓广思考
如何作出圆内接正方形呢?
拓广思考
还可以怎么作正六边形和正方形呢?
拓广思考
类比,如何作出圆内接正八边形呢
拓广思考
还可以用什么方法作出圆内接正八边形 ?
拓广思考
你还可以用什么方法作出圆内接八边形吗?
拓广思考
照此方法依次可作正十六边形、正三十二边形、正六十四边形
方法总结
先用量角器画一个中心角,然后在圆上依次截取等于该中心角所对弧的等弧,于是得到圆的等分点,相对比较简单,但画图的误差积累到最后一个等分点,误差较大.
2
尺规作图,虽然精确,但不是任意等分圆周都能用这种方法,而且作图时存在误差.
3
1
依次画出相等的中心角来等分圆. 比较准确,但是麻烦. 由于限制条件少,可以作为画圆内接正多边形的通法.
本节课提到的其他一些方法只适用于某些特殊的正多边形.
4
练习
如何在半径为 的⊙ 中作出内接正九边形呢?
1
练习
如何借助圆画出一个五角星呢?
2
练习
用等分圆的方法画出下列图案.
3
欣赏图片
用等分圆的方法可以画出如下美丽的图案,欣赏一下.
课
堂
小
结
利用等分圆的方法我们可以画出正多边形.
1
对于一些特殊的正多边形比如正六边形,正方形等可以使用尺规作图的方法来作图.
2
借助圆和正多边形也可以设计一些美丽的图案.
3
通用的方法:用量角器等分圆.
依次画出相等的中心角来等分圆.
先用量角器画一个中心角,然后在圆上依次截取等于该中心角所对弧的等弧来等分圆.
课后作业
尝试用不同的方法画一个正六边形.
1
用等分圆的方法画出下列图案,并给它们涂上你喜欢的颜色.
2
尝试用等分圆周的方法设计一些美丽的图案.
3
同课章节目录
