人教版九年级数学上册《直线和圆的位置关系》第2课时教学课件(共22张PPT)
文档属性
| 名称 | 人教版九年级数学上册《直线和圆的位置关系》第2课时教学课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 06:59:25 | ||
图片预览





文档简介
(共22张PPT)
(第二课时)
直线和圆的位置关系
直线和圆相交
直线和圆相离
直线和圆相切
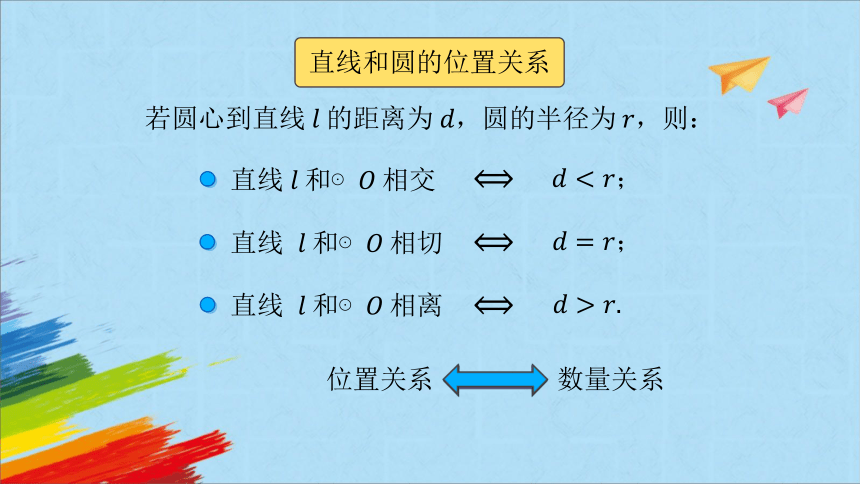
直线和圆的位置关系
若圆心到直线的距离为,圆的半径为,则:
直线 和⊙相切
直线 和⊙相离
直线和圆的位置关系
直线和⊙相交
位置关系
数量关系
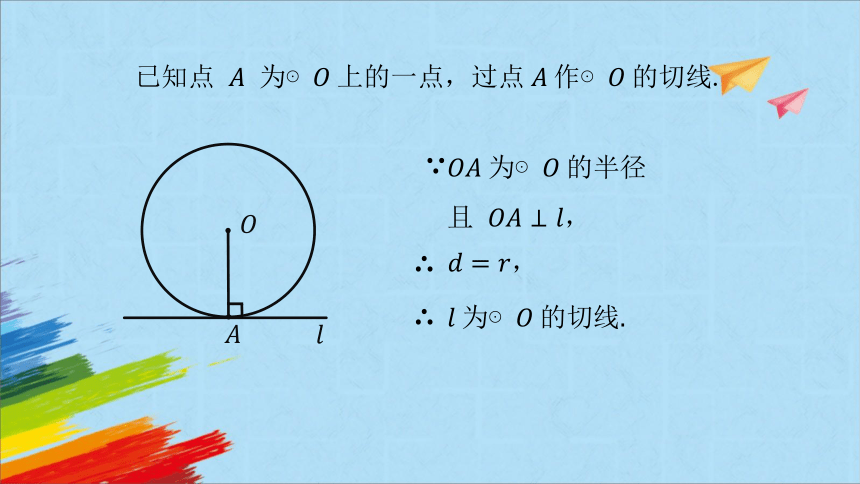
已知点 为⊙上的一点,过点作⊙的切线.
⊙的半径
且 ,
⊙ 的切线.
切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
1
直线经过半径外端点
(直线与圆有公共点)
2
直线垂直于这条半径
直线与圆相切
⊙的半径
且 于,
⊙ 的切线.
圆的切线的判定方法
定义 —— 与圆只有一个公共点;
数量关系 —— ;
位置关系 —— 经过半径外端且垂直于这条半径.
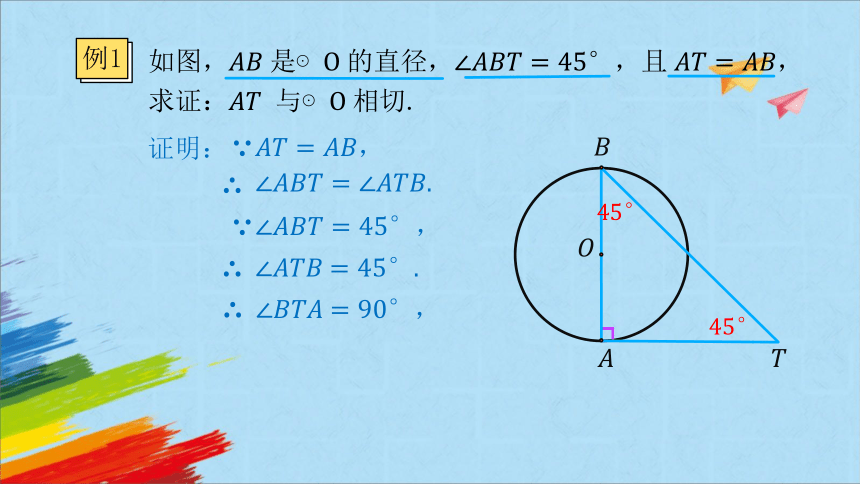
如图,是⊙直径,且,求证: 与⊙相切.
例1
证明:
.
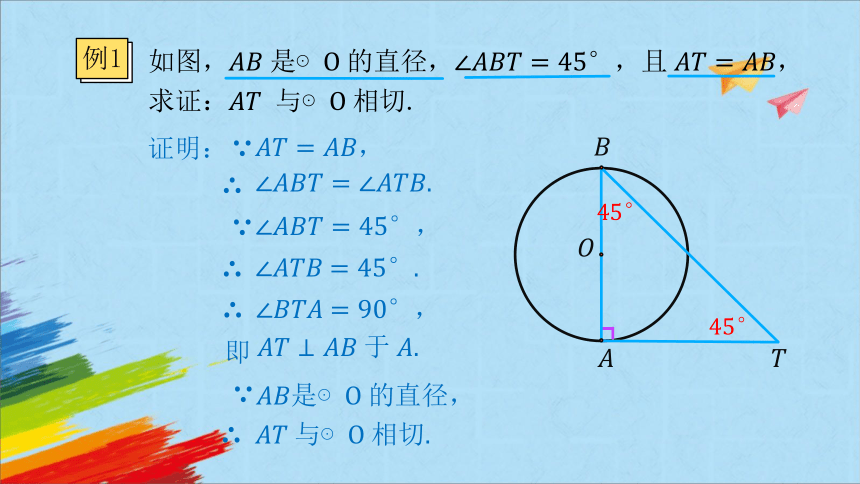
如图,是⊙直径,且,求证: 与⊙相切.
证明:
.
即
.
⊙的直径,
⊙.
例1
如图,直线经过⊙的点,并且, 求证: 是⊙的切线.
例2
如图,直线经过⊙的点,并且, 求证: 是⊙的切线.
,,
证明:
.
⊙的半径,
⊙.
连接
例2
如图,△内的中点,求证: 分别是小圆的切线.
例3
如图,△内的中点,求证: 分别是小圆的切线.
例3
如图,△内的中点,求证: 分别是小圆的切线.
例3
如图,△内的中点,求证: 分别是小圆的切线.
例3
如图,△内的中点,求证: 分别是小圆的切线.
例3
如图,△内的中点,求证: 分别是小圆的切线.
与小圆相切
与小圆公共点未明确
过圆心作的垂线段
与小圆相切
与小圆的公共点
并证明
例3
如图,△内的中点,求证: 分别是小圆的切线.
例3
的中点,
证明:
为小圆的半径,
小圆相切.
连接,作 .
△大圆,
.
,
,
.
连,可得
小圆相切.
当证明某直线是圆的切线时,如果已知直线过圆上一点,则作出过这一点的半径,证明直线垂直于半径,简记为“连半径,证垂直”;如果直线和圆的公共点没有确定,则应过圆心作直线的垂线,证明圆心到直线的距离等于半径,简记为“作垂直,证半径”.
课
堂
小
结
2
一般的,当证明某直线是圆的切线时,如果已知直线过圆上一点,应“连半径,证垂直”,即作出过这一点的半径,证明直线垂直于半径;如果直线和圆的公共点没有确定,应“作垂直,证半径”,即应过圆心作直线的垂线,证明圆心到直线的距离等于半径.
1
直线与圆相切是直线与圆位置关系中最特殊的一种;
课后作业
如图, 是⊙外一点,的延长线交⊙于点 点在圆上,且, 求证:直线是⊙的切线.
1
课后作业
如图,点是的平分线上任意一点,过 作 于,以为半径作. 补全图形,判断 与⊙ 的位置关系,并证明你的结论.
2
(第二课时)
直线和圆的位置关系
直线和圆相交
直线和圆相离
直线和圆相切
直线和圆的位置关系
若圆心到直线的距离为,圆的半径为,则:
直线 和⊙相切
直线 和⊙相离
直线和圆的位置关系
直线和⊙相交
位置关系
数量关系
已知点 为⊙上的一点,过点作⊙的切线.
⊙的半径
且 ,
⊙ 的切线.
切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
1
直线经过半径外端点
(直线与圆有公共点)
2
直线垂直于这条半径
直线与圆相切
⊙的半径
且 于,
⊙ 的切线.
圆的切线的判定方法
定义 —— 与圆只有一个公共点;
数量关系 —— ;
位置关系 —— 经过半径外端且垂直于这条半径.
如图,是⊙直径,且,求证: 与⊙相切.
例1
证明:
.
如图,是⊙直径,且,求证: 与⊙相切.
证明:
.
即
.
⊙的直径,
⊙.
例1
如图,直线经过⊙的点,并且, 求证: 是⊙的切线.
例2
如图,直线经过⊙的点,并且, 求证: 是⊙的切线.
,,
证明:
.
⊙的半径,
⊙.
连接
例2
如图,△内的中点,求证: 分别是小圆的切线.
例3
如图,△内的中点,求证: 分别是小圆的切线.
例3
如图,△内的中点,求证: 分别是小圆的切线.
例3
如图,△内的中点,求证: 分别是小圆的切线.
例3
如图,△内的中点,求证: 分别是小圆的切线.
例3
如图,△内的中点,求证: 分别是小圆的切线.
与小圆相切
与小圆公共点未明确
过圆心作的垂线段
与小圆相切
与小圆的公共点
并证明
例3
如图,△内的中点,求证: 分别是小圆的切线.
例3
的中点,
证明:
为小圆的半径,
小圆相切.
连接,作 .
△大圆,
.
,
,
.
连,可得
小圆相切.
当证明某直线是圆的切线时,如果已知直线过圆上一点,则作出过这一点的半径,证明直线垂直于半径,简记为“连半径,证垂直”;如果直线和圆的公共点没有确定,则应过圆心作直线的垂线,证明圆心到直线的距离等于半径,简记为“作垂直,证半径”.
课
堂
小
结
2
一般的,当证明某直线是圆的切线时,如果已知直线过圆上一点,应“连半径,证垂直”,即作出过这一点的半径,证明直线垂直于半径;如果直线和圆的公共点没有确定,应“作垂直,证半径”,即应过圆心作直线的垂线,证明圆心到直线的距离等于半径.
1
直线与圆相切是直线与圆位置关系中最特殊的一种;
课后作业
如图, 是⊙外一点,的延长线交⊙于点 点在圆上,且, 求证:直线是⊙的切线.
1
课后作业
如图,点是的平分线上任意一点,过 作 于,以为半径作. 补全图形,判断 与⊙ 的位置关系,并证明你的结论.
2
同课章节目录
