人教版九年级数学上册《直线和圆的位置关系》第3课时教学课件(共30张PPT)
文档属性
| 名称 | 人教版九年级数学上册《直线和圆的位置关系》第3课时教学课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 06:58:18 | ||
图片预览






文档简介
(共30张PPT)
(第三课时)
直线与圆的位置关系
复习回顾
圆的切线是如何定义的?
1
如果直线和圆只有一个公共点,那么这条直线叫圆的切线.
复习回顾
判断一条直线是圆的切线有哪些方法?
2
当直线和圆只有唯一公共点的时候,这条直线是圆的切线;
方法
当圆心到直线的距离等于半径的时候,这条直线是圆的切线;
方法
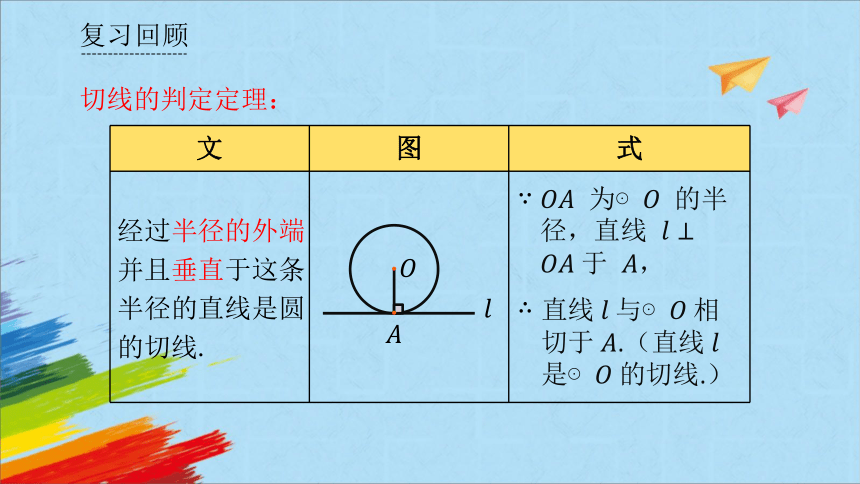
切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
方法
复习回顾
切线的判定定理:
文 图 式
经过半径的外端并且垂直于这条半径的直线是圆的切线.
为⊙ 的半径,直线 于 ,
直线 与⊙ 相切于 .(直线 是⊙ 的切线.)
探索性质
根据切线的定义我们可以得到切线的如下性质:
切线 和⊙ 有且只有一个公共点 ;
圆心 到切线 的距离等于圆的半径.
1
2
探索性质
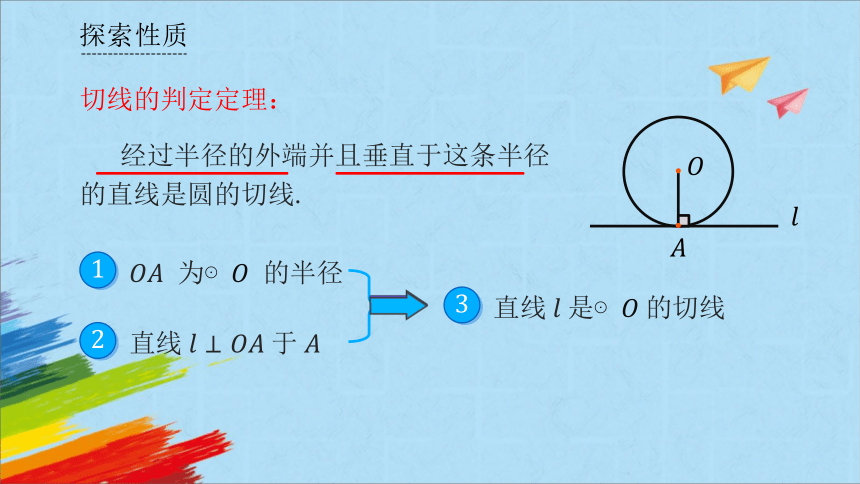
切线的判定定理:
经过半径的外端并且垂直于这条半径
的直线是圆的切线.
为⊙ 的半径
1
2
直线 于
3
直线 是⊙ 的切线
探索性质
如图,已知直线 是⊙ 的切线,切点为 ,
连接 ,直线 吗?
问
探索性质
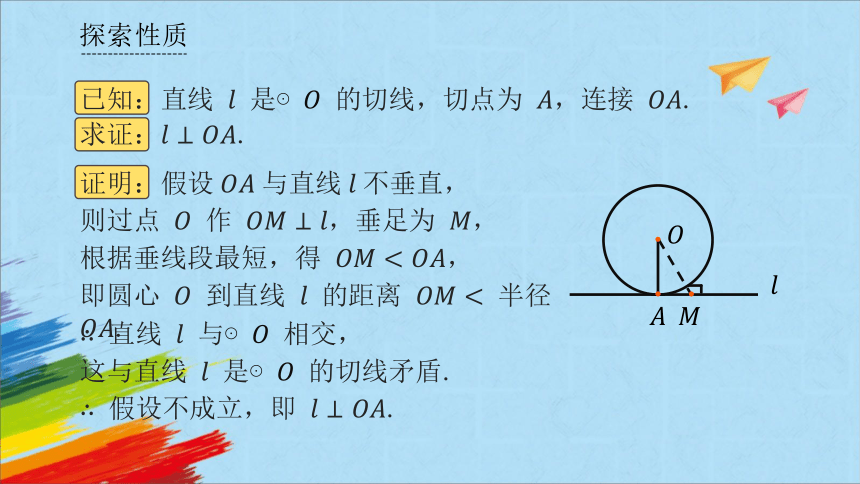
已知:直线 是⊙ 的切线,切点为 ,连接 .
求证:.
证明:假设 与直线 不垂直,
则过点 作 ,垂足为 ,
根据垂线段最短,得 ,
即圆心 到直线 的距离 半径 .
直线 与⊙ 相交,
这与直线 是⊙ 的切线矛盾.
假设不成立,即 .
探索性质
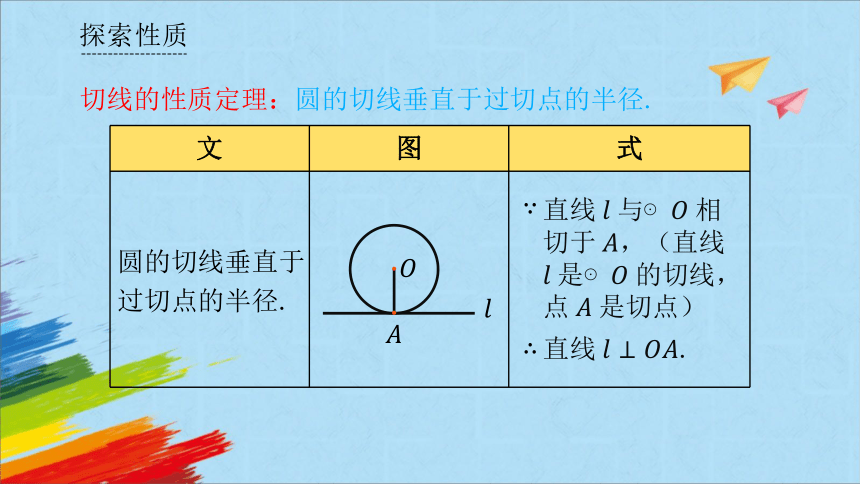
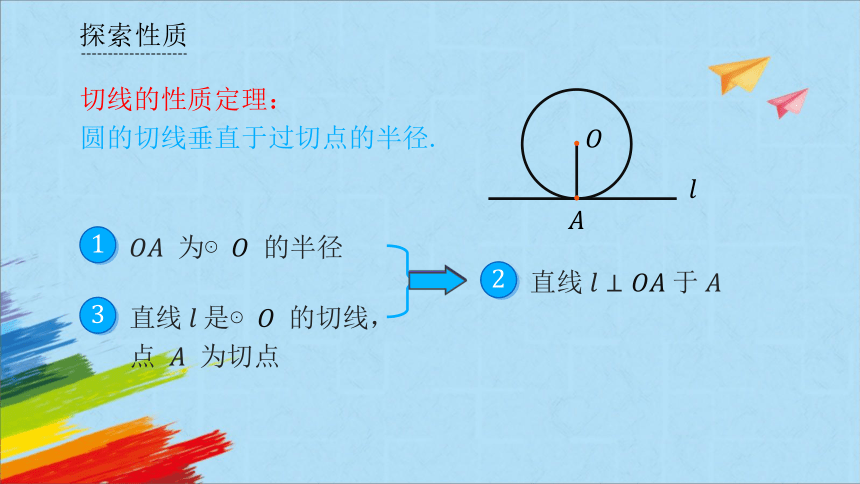
切线的性质定理:圆的切线垂直于过切点的半径.
文 图 式
圆的切线垂直于过切点的半径.
直线 与⊙ 相切于 ,(直线
是⊙ 的切线,点 是切点)
直线 .
切线的性质定理:
圆的切线垂直于过切点的半径.
探索性质
为⊙ 的半径
1
3
直线 是⊙ 的切线,
点 为切点
2
直线 于
探索性质
如图,已知⊙ 的切线 ,但切点未知,你能作出切点 吗?
于
于 ,这里又有 于 ,
垂足 就是切点 .
问
探索性质
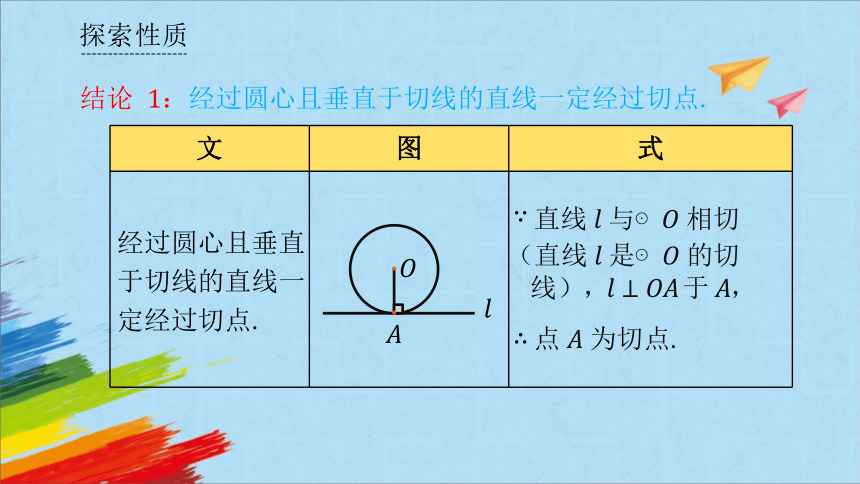
结论 :经过圆心且垂直于切线的直线一定经过切点.
文 图 式
经过圆心且垂直于切线的直线一定经过切点.
点 为切点.
直线 与⊙ 相切
(直线 是⊙ 的切
线), 于 ,
结论 :
经过圆心且垂直于切线的直线一定经过切点.
探索性质
直线 是⊙ 的切线
3
直线 于
2
为⊙ 的半径
1
结论 :
经过切点垂直于切线的直线一定经过圆心.
探索性质
(请同学们课后研究)
性质的应用
如图,△ 为等腰三角形, 是底边 的中点,腰 与⊙ 相切于点 .
求证: 是⊙ 的切线.
例1
如图,△ 为等腰三角形, 是底边 的中点,腰 与⊙ 相切于点 .
求证: 是⊙ 的切线.
性质的应用
证明:如图,过点 作 ,垂足为 ,
连接.
⊙ 与 相切于点 ,
.
又△ 为等腰三角形, 是底边 的中点,
是 的平分线.
例1
如图,△ 为等腰三角形, 是底边 的中点,腰 与⊙ 相切于点 .
求证: 是⊙ 的切线.
性质的应用
又 ,
,即 是⊙ 的半径.
为⊙ 的半径, 于 ,
与⊙ 相切.
例1
作过切点的半径
如图, 为⊙ 的直径, 是弦, 是 的中点,
过点 作⊙ 的切线,交 的延长线于点 .
求证:∥;
若 ,求弦 的长.
性质的应用
例2
性质的应用
例2
由 是切点可想到……
由 是 的中点可想到……
如图, 为⊙ 的直径, 是弦, 是 的中点,
过点 作⊙ 的切线,交 的延长线于点 .
求证:∥;
若 ,求弦 的长.
由 是⊙ 的直径可想到……
分析
性质的应用
证明:连接 .
切⊙ 于 ,
.
.
例2
如图, 为⊙ 的直径, 是弦, 是 的中点,
过点 作⊙ 的切线,交 的延长线于点 .
求证:∥;
性质的应用
,
又 ,
,
,
∥.
是 的中点,
,
例2
如图, 为⊙ 的直径, 是弦, 是 的中点,
过点 作⊙ 的切线,交 的延长线于点 .
求证:∥;
如图, 为⊙ 的直径, 是弦, 是 的中点,
过点 作⊙ 的切线,交 的延长线于点 .
若 ,求弦 的长.
性质的应用
,
又 ,
△ 为等边三角形.
解:连接 .
.
例2
性质的应用
由 ,设垂足为 ,
在 △ 中,可得 ,
.
.
例2
如图, 为⊙ 的直径, 是弦, 是 的中点,
过点 作⊙ 的切线,交 的延长线于点 .
若 ,求弦 的长.
课
堂
小
结
切线的判定与性质的关系:
1
切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
为⊙ 的半径
1
直线 于
2
直线 是⊙ 的切线
3
课
堂
小
结
切线的判定与性质的关系:
1
切线的性质定理:
圆的切线垂直于过切点的半径.
为⊙ 的半径
1
2
直线 于
3
直线 是⊙ 的切线,
点 为切点
课
堂
小
结
切线的判定与性质的关系:
1
结论:
结论 :经过圆心且垂直于切线的直线必过切点;
直线 是⊙ 的切线
3
直线 于
2
1
为⊙ 的半径
结论:经过切点垂直于切线的直线一定经过圆心.
切点位置不确定,可以过圆心作切线的垂线,垂足就是切点.
课
堂
小
结
已知圆的切线,要利用切线的性质时常添的常用辅助线:
2
切点的位置确定,常常是连接圆心和切点;
布置作业
如图,已知⊙ 的直径 与弦 的夹角为 ,过点
的切线 与 的延长线相交于点 ,则 .
1
布置作业
如图,已知⊙ 的半径为 ,直线 是⊙ 的切线, 交 于点 ,且,则 的长为 .
2
如图,在 △ 中,,点 在 上,,以 为半径的⊙ 与 相切于点 ,交 于
点 ,求弦 的长.
布置作业
3
(第三课时)
直线与圆的位置关系
复习回顾
圆的切线是如何定义的?
1
如果直线和圆只有一个公共点,那么这条直线叫圆的切线.
复习回顾
判断一条直线是圆的切线有哪些方法?
2
当直线和圆只有唯一公共点的时候,这条直线是圆的切线;
方法
当圆心到直线的距离等于半径的时候,这条直线是圆的切线;
方法
切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
方法
复习回顾
切线的判定定理:
文 图 式
经过半径的外端并且垂直于这条半径的直线是圆的切线.
为⊙ 的半径,直线 于 ,
直线 与⊙ 相切于 .(直线 是⊙ 的切线.)
探索性质
根据切线的定义我们可以得到切线的如下性质:
切线 和⊙ 有且只有一个公共点 ;
圆心 到切线 的距离等于圆的半径.
1
2
探索性质
切线的判定定理:
经过半径的外端并且垂直于这条半径
的直线是圆的切线.
为⊙ 的半径
1
2
直线 于
3
直线 是⊙ 的切线
探索性质
如图,已知直线 是⊙ 的切线,切点为 ,
连接 ,直线 吗?
问
探索性质
已知:直线 是⊙ 的切线,切点为 ,连接 .
求证:.
证明:假设 与直线 不垂直,
则过点 作 ,垂足为 ,
根据垂线段最短,得 ,
即圆心 到直线 的距离 半径 .
直线 与⊙ 相交,
这与直线 是⊙ 的切线矛盾.
假设不成立,即 .
探索性质
切线的性质定理:圆的切线垂直于过切点的半径.
文 图 式
圆的切线垂直于过切点的半径.
直线 与⊙ 相切于 ,(直线
是⊙ 的切线,点 是切点)
直线 .
切线的性质定理:
圆的切线垂直于过切点的半径.
探索性质
为⊙ 的半径
1
3
直线 是⊙ 的切线,
点 为切点
2
直线 于
探索性质
如图,已知⊙ 的切线 ,但切点未知,你能作出切点 吗?
于
于 ,这里又有 于 ,
垂足 就是切点 .
问
探索性质
结论 :经过圆心且垂直于切线的直线一定经过切点.
文 图 式
经过圆心且垂直于切线的直线一定经过切点.
点 为切点.
直线 与⊙ 相切
(直线 是⊙ 的切
线), 于 ,
结论 :
经过圆心且垂直于切线的直线一定经过切点.
探索性质
直线 是⊙ 的切线
3
直线 于
2
为⊙ 的半径
1
结论 :
经过切点垂直于切线的直线一定经过圆心.
探索性质
(请同学们课后研究)
性质的应用
如图,△ 为等腰三角形, 是底边 的中点,腰 与⊙ 相切于点 .
求证: 是⊙ 的切线.
例1
如图,△ 为等腰三角形, 是底边 的中点,腰 与⊙ 相切于点 .
求证: 是⊙ 的切线.
性质的应用
证明:如图,过点 作 ,垂足为 ,
连接.
⊙ 与 相切于点 ,
.
又△ 为等腰三角形, 是底边 的中点,
是 的平分线.
例1
如图,△ 为等腰三角形, 是底边 的中点,腰 与⊙ 相切于点 .
求证: 是⊙ 的切线.
性质的应用
又 ,
,即 是⊙ 的半径.
为⊙ 的半径, 于 ,
与⊙ 相切.
例1
作过切点的半径
如图, 为⊙ 的直径, 是弦, 是 的中点,
过点 作⊙ 的切线,交 的延长线于点 .
求证:∥;
若 ,求弦 的长.
性质的应用
例2
性质的应用
例2
由 是切点可想到……
由 是 的中点可想到……
如图, 为⊙ 的直径, 是弦, 是 的中点,
过点 作⊙ 的切线,交 的延长线于点 .
求证:∥;
若 ,求弦 的长.
由 是⊙ 的直径可想到……
分析
性质的应用
证明:连接 .
切⊙ 于 ,
.
.
例2
如图, 为⊙ 的直径, 是弦, 是 的中点,
过点 作⊙ 的切线,交 的延长线于点 .
求证:∥;
性质的应用
,
又 ,
,
,
∥.
是 的中点,
,
例2
如图, 为⊙ 的直径, 是弦, 是 的中点,
过点 作⊙ 的切线,交 的延长线于点 .
求证:∥;
如图, 为⊙ 的直径, 是弦, 是 的中点,
过点 作⊙ 的切线,交 的延长线于点 .
若 ,求弦 的长.
性质的应用
,
又 ,
△ 为等边三角形.
解:连接 .
.
例2
性质的应用
由 ,设垂足为 ,
在 △ 中,可得 ,
.
.
例2
如图, 为⊙ 的直径, 是弦, 是 的中点,
过点 作⊙ 的切线,交 的延长线于点 .
若 ,求弦 的长.
课
堂
小
结
切线的判定与性质的关系:
1
切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
为⊙ 的半径
1
直线 于
2
直线 是⊙ 的切线
3
课
堂
小
结
切线的判定与性质的关系:
1
切线的性质定理:
圆的切线垂直于过切点的半径.
为⊙ 的半径
1
2
直线 于
3
直线 是⊙ 的切线,
点 为切点
课
堂
小
结
切线的判定与性质的关系:
1
结论:
结论 :经过圆心且垂直于切线的直线必过切点;
直线 是⊙ 的切线
3
直线 于
2
1
为⊙ 的半径
结论:经过切点垂直于切线的直线一定经过圆心.
切点位置不确定,可以过圆心作切线的垂线,垂足就是切点.
课
堂
小
结
已知圆的切线,要利用切线的性质时常添的常用辅助线:
2
切点的位置确定,常常是连接圆心和切点;
布置作业
如图,已知⊙ 的直径 与弦 的夹角为 ,过点
的切线 与 的延长线相交于点 ,则 .
1
布置作业
如图,已知⊙ 的半径为 ,直线 是⊙ 的切线, 交 于点 ,且,则 的长为 .
2
如图,在 △ 中,,点 在 上,,以 为半径的⊙ 与 相切于点 ,交 于
点 ,求弦 的长.
布置作业
3
同课章节目录
