人教版九年级数学上册《直线和圆的位置关系》第4课时教学课件 (共35张PPT)
文档属性
| 名称 | 人教版九年级数学上册《直线和圆的位置关系》第4课时教学课件 (共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 07:00:14 | ||
图片预览







文档简介
(共35张PPT)
(第四课时)
直线与圆的位置关系
复习引入
在同一个平面内,有一点 和⊙,过点 能否作⊙ 的切线?如果能,可以作几条切线?如果不能,说明理由.
问题1
点 和⊙ 的位置关系
点 在⊙ 内
点 在⊙ 上
点 在⊙ 外
点 在⊙ 内
过点 的直线都与圆相交,所以不存在过 点的直线与⊙ 相切.
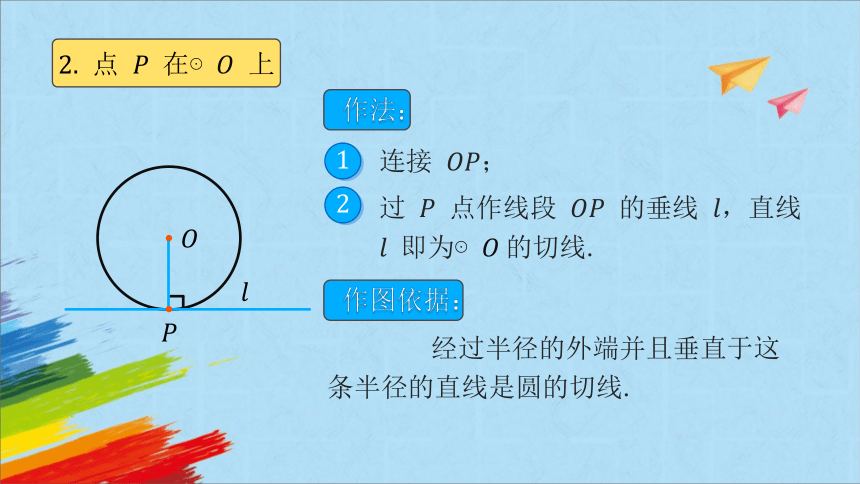
点 在⊙ 上
作法:
连接 ;
1
过 点作线段 的垂线 ,直线 即为⊙ 的切线.
2
作图依据:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
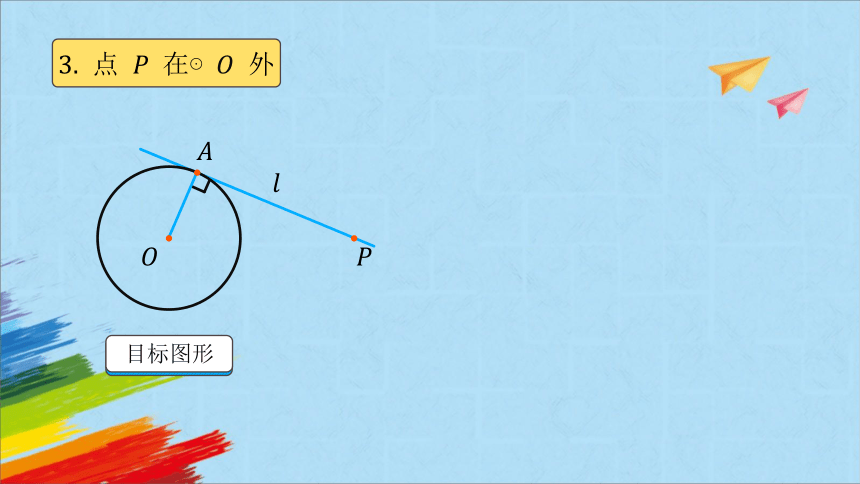
点 在⊙ 外
目标图形
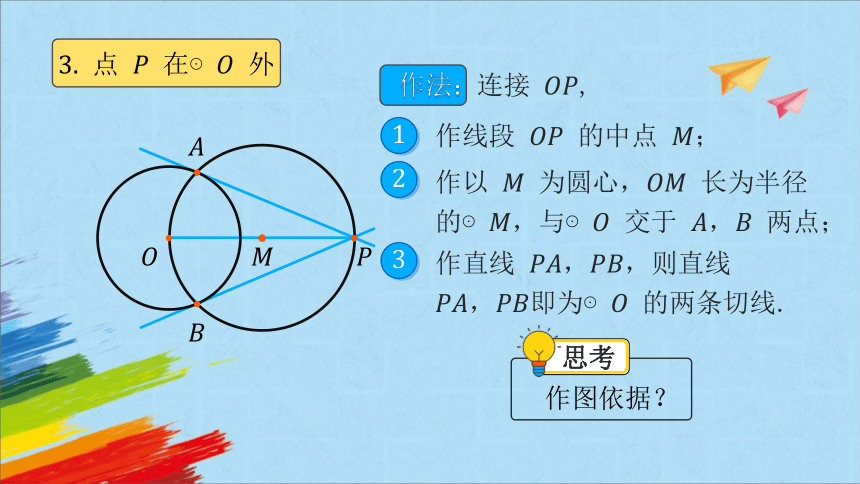
点 在⊙ 外
作法:
作线段 的中点 ;
1
连接 ,
作以 为圆心, 长为半径的⊙,与⊙ 交于 两点;
2
作直线 ,则直线 即为⊙ 的两条切线.
3
作图依据?
思考
作图依据:
直径所对的圆周角是直角;
1
经过半径的外端并且垂直于这条半径的直线是圆的切线;
2
两点确定一条直线.
3
点 在⊙ 外
总结
点 在⊙ 内,过 点,不存在圆的切线;
点 在⊙ 上,过 点,可以作圆的一条切线;
点 在⊙ 外,过 点,可以作圆的两条切线.
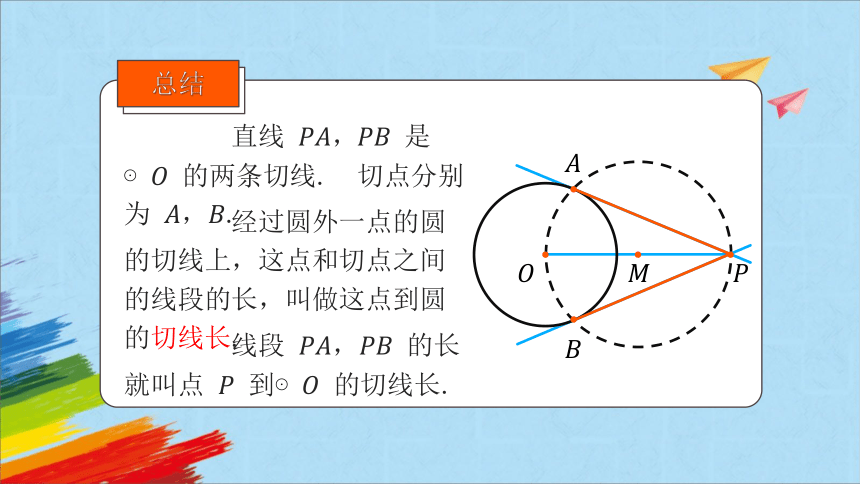
总结
直线 是⊙ 的两条切线. 切点分别为 .
经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.
线段 的长就叫点 到⊙ 的切线长.
问题2
请同学思考圆的切线与切线长的区别.
切线 切线长
切线是直线
无法度量
切线长是切线上一条线段的长,
即圆外一点与切点之间的距离
可以度量
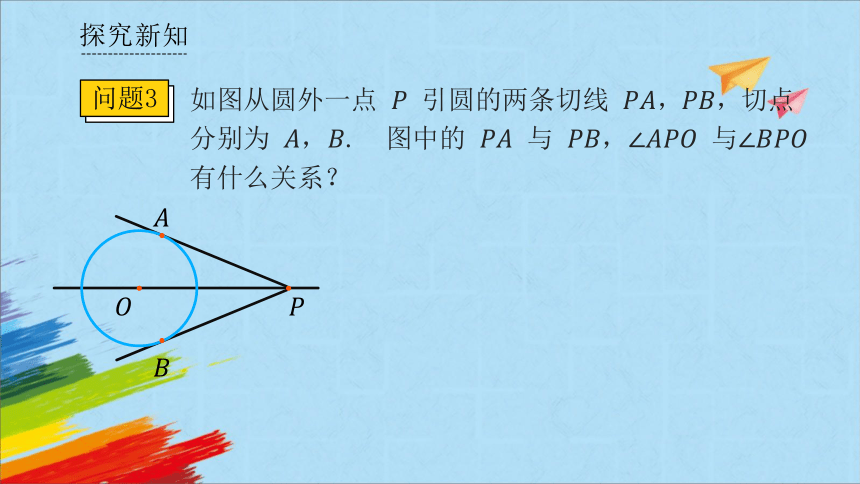
探究新知
如图从圆外一点 引圆的两条切线 ,切点分别为 . 图中的 与 , 与 有什么关系?
问题3
方法一:
利用圆的轴对称性
半透明的纸上画出从圆外一点 引圆的两条切线 的图形,切点分别为 .
沿着直线 将图形对折,图中 与 , 与 有什么关系?
方法二:
证明
连接 .
和 是⊙ 的两条切线,
.
在 △ 与 △ 中,
,
,
切线长定理:
文字语言
符号语言
和 是⊙ 的两条切线, 为切点.
从圆外一点可以引圆的两条切线,它们的切线长
相等,这点和圆心的连线平分两条切线的夹角.
图形语言
切线长定理:
圆外一点引圆的两条切线
线段相等
角相等
连接 和 ,通过切线长的证明,还能得到什么结论?
.
.
连接两切点 ,交 于 点,还能得什么结论?
.
.
.
.
=
=
=
=
基本图形
连接两切点 ,交 于 点,还能得什么结论?
设 与⊙ 的交点分别为 ,还能得什么结论?
问题4
如何在一块三角形的铁皮上面截下一块圆形的用料,并且使得截下来的圆与三角形的三边都相切?
圆心到三边的距离相等,
所以圆心是三角形三条角
平分线的交点.
半径即圆心到三边的距离.
分析
分别作 的角平分线
角平分线 的交点记为 ;
1
过 点作 于点 ;
2
以点 为圆心, 长为半径作⊙.
3
则⊙ 即为所求.
作法
与三角形各边都相切的圆叫做三角形的内切圆. 如⊙ 是△ 的内切圆,内切圆的圆心 是三角形三条角平分线的交点,叫三角形的内心.
如图,△ 的内切圆⊙ 与 分别相切于点 . 若 .
例1
求 的长;
1
若△ 的面积为 ,求△ 内切圆的半径.
2
都与⊙ 相切.
由切线长定理,可得
.
设 则
.
解:
⊙ 是△ 的内切圆,
求 的长;
1
解得
.
因此
.
由 得
若△ 的面积为 ,求△ 内切圆的半径.
2
解:
△△△△.
△.
.
三角形内切圆半径公式:
其中 为三角形的面积; 为三角形的周长.
△
可证四边形 是正方形.
解:
⊙ 是△ 的内切圆.
其中 为直角三角形的直角边长; 为斜边长.
归纳
一般三角形内切圆半径公式: .
其中 为三角形的面积; 为三角形的周长.
1
特殊的直角三角形内切圆半径公式:
或 .
其中 为三角形的直角边长; 为斜边长.
2
问题5
三角形的外接圆与三角形的内切圆,有什么区别呢?
图形 名称 性质 位置 角度关系
外心:三角形外接圆的圆心(或三角形三边中垂线的交点).
内心:三角形内切圆的圆心(或三角形三内角平分线的交点).
三角形外心到三角形的三个顶点的距离相等. 即.
三角形内心到三角形的三边的距离相等. 即
.
锐角三角形的外心在形内;
直角三角形的外心在斜边中点;
钝角三角形的外心在形外.
三角形的内心一定在三角形内.
“接”或“切”是说明多边形的顶点或边与圆的位置关系:
多边形的顶点都在圆上叫“接”,
多边形的边都与圆相切叫“切”.
课
堂
小
结
发现过圆外一点能引圆的两条切线
切线长定理的证明及三种语言表达
切线长定理在三角形应用
过一点能否作已知圆的切线
一般三角形和直角三角形的内切圆半径公式
在与三角形外接圆比较中加深对内切圆的理解
课后作业
如图, 是△ 的内心.
若,求 的度数;
若△ 的内切圆半径为 ,△ 的周长 ,求△ 的面积.
1
如图, 是⊙ 的切线, 为切点, 是⊙ 的直径,. 求 的度数.
2
如图, 分别与⊙ 相切于 三点,
且 ∥. 求 的长.
3
(第四课时)
直线与圆的位置关系
复习引入
在同一个平面内,有一点 和⊙,过点 能否作⊙ 的切线?如果能,可以作几条切线?如果不能,说明理由.
问题1
点 和⊙ 的位置关系
点 在⊙ 内
点 在⊙ 上
点 在⊙ 外
点 在⊙ 内
过点 的直线都与圆相交,所以不存在过 点的直线与⊙ 相切.
点 在⊙ 上
作法:
连接 ;
1
过 点作线段 的垂线 ,直线 即为⊙ 的切线.
2
作图依据:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
点 在⊙ 外
目标图形
点 在⊙ 外
作法:
作线段 的中点 ;
1
连接 ,
作以 为圆心, 长为半径的⊙,与⊙ 交于 两点;
2
作直线 ,则直线 即为⊙ 的两条切线.
3
作图依据?
思考
作图依据:
直径所对的圆周角是直角;
1
经过半径的外端并且垂直于这条半径的直线是圆的切线;
2
两点确定一条直线.
3
点 在⊙ 外
总结
点 在⊙ 内,过 点,不存在圆的切线;
点 在⊙ 上,过 点,可以作圆的一条切线;
点 在⊙ 外,过 点,可以作圆的两条切线.
总结
直线 是⊙ 的两条切线. 切点分别为 .
经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.
线段 的长就叫点 到⊙ 的切线长.
问题2
请同学思考圆的切线与切线长的区别.
切线 切线长
切线是直线
无法度量
切线长是切线上一条线段的长,
即圆外一点与切点之间的距离
可以度量
探究新知
如图从圆外一点 引圆的两条切线 ,切点分别为 . 图中的 与 , 与 有什么关系?
问题3
方法一:
利用圆的轴对称性
半透明的纸上画出从圆外一点 引圆的两条切线 的图形,切点分别为 .
沿着直线 将图形对折,图中 与 , 与 有什么关系?
方法二:
证明
连接 .
和 是⊙ 的两条切线,
.
在 △ 与 △ 中,
,
,
切线长定理:
文字语言
符号语言
和 是⊙ 的两条切线, 为切点.
从圆外一点可以引圆的两条切线,它们的切线长
相等,这点和圆心的连线平分两条切线的夹角.
图形语言
切线长定理:
圆外一点引圆的两条切线
线段相等
角相等
连接 和 ,通过切线长的证明,还能得到什么结论?
.
.
连接两切点 ,交 于 点,还能得什么结论?
.
.
.
.
=
=
=
=
基本图形
连接两切点 ,交 于 点,还能得什么结论?
设 与⊙ 的交点分别为 ,还能得什么结论?
问题4
如何在一块三角形的铁皮上面截下一块圆形的用料,并且使得截下来的圆与三角形的三边都相切?
圆心到三边的距离相等,
所以圆心是三角形三条角
平分线的交点.
半径即圆心到三边的距离.
分析
分别作 的角平分线
角平分线 的交点记为 ;
1
过 点作 于点 ;
2
以点 为圆心, 长为半径作⊙.
3
则⊙ 即为所求.
作法
与三角形各边都相切的圆叫做三角形的内切圆. 如⊙ 是△ 的内切圆,内切圆的圆心 是三角形三条角平分线的交点,叫三角形的内心.
如图,△ 的内切圆⊙ 与 分别相切于点 . 若 .
例1
求 的长;
1
若△ 的面积为 ,求△ 内切圆的半径.
2
都与⊙ 相切.
由切线长定理,可得
.
设 则
.
解:
⊙ 是△ 的内切圆,
求 的长;
1
解得
.
因此
.
由 得
若△ 的面积为 ,求△ 内切圆的半径.
2
解:
△△△△.
△.
.
三角形内切圆半径公式:
其中 为三角形的面积; 为三角形的周长.
△
可证四边形 是正方形.
解:
⊙ 是△ 的内切圆.
其中 为直角三角形的直角边长; 为斜边长.
归纳
一般三角形内切圆半径公式: .
其中 为三角形的面积; 为三角形的周长.
1
特殊的直角三角形内切圆半径公式:
或 .
其中 为三角形的直角边长; 为斜边长.
2
问题5
三角形的外接圆与三角形的内切圆,有什么区别呢?
图形 名称 性质 位置 角度关系
外心:三角形外接圆的圆心(或三角形三边中垂线的交点).
内心:三角形内切圆的圆心(或三角形三内角平分线的交点).
三角形外心到三角形的三个顶点的距离相等. 即.
三角形内心到三角形的三边的距离相等. 即
.
锐角三角形的外心在形内;
直角三角形的外心在斜边中点;
钝角三角形的外心在形外.
三角形的内心一定在三角形内.
“接”或“切”是说明多边形的顶点或边与圆的位置关系:
多边形的顶点都在圆上叫“接”,
多边形的边都与圆相切叫“切”.
课
堂
小
结
发现过圆外一点能引圆的两条切线
切线长定理的证明及三种语言表达
切线长定理在三角形应用
过一点能否作已知圆的切线
一般三角形和直角三角形的内切圆半径公式
在与三角形外接圆比较中加深对内切圆的理解
课后作业
如图, 是△ 的内心.
若,求 的度数;
若△ 的内切圆半径为 ,△ 的周长 ,求△ 的面积.
1
如图, 是⊙ 的切线, 为切点, 是⊙ 的直径,. 求 的度数.
2
如图, 分别与⊙ 相切于 三点,
且 ∥. 求 的长.
3
同课章节目录
