等腰三角形
图片预览

文档简介
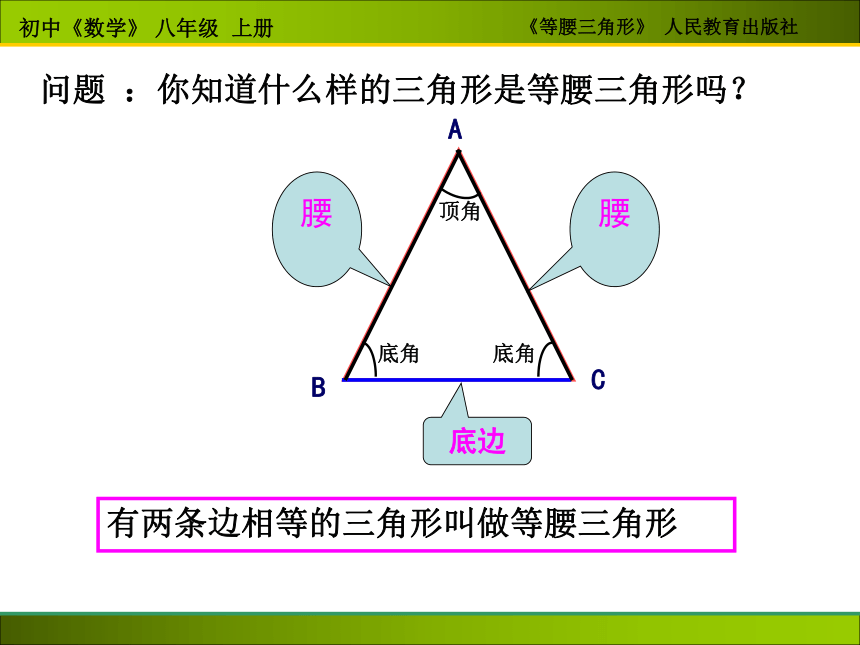
课件18张PPT。初中《数学》 八年级 上册《等腰三角形》 人民教育出版社等腰三角形韶关市七中 郭红峰 问题 :你知道什么样的三角形是等腰三角形吗?
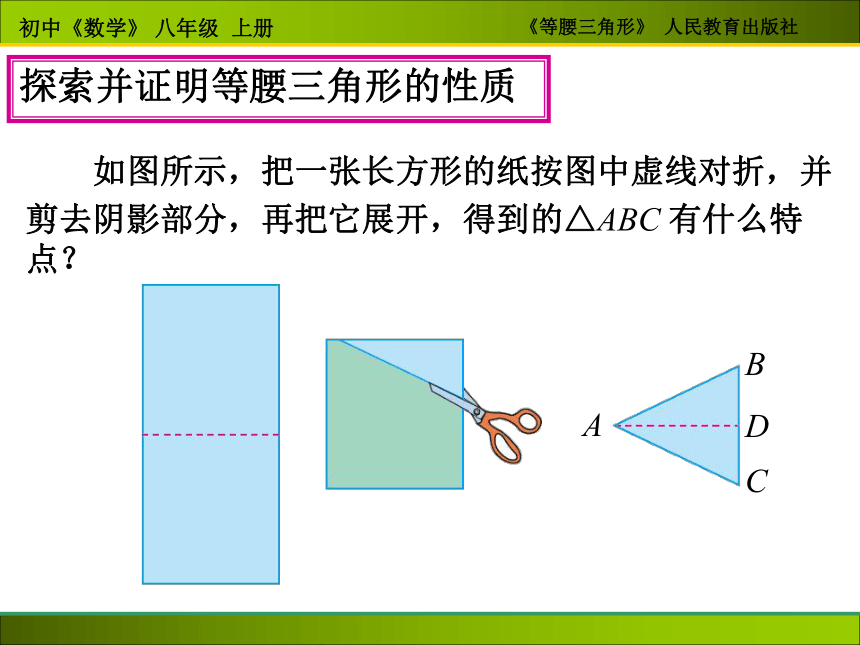
底边底角底角顶角有两条边相等的三角形叫做等腰三角形 如图所示,把一张长方形的纸按图中虚线对折,并
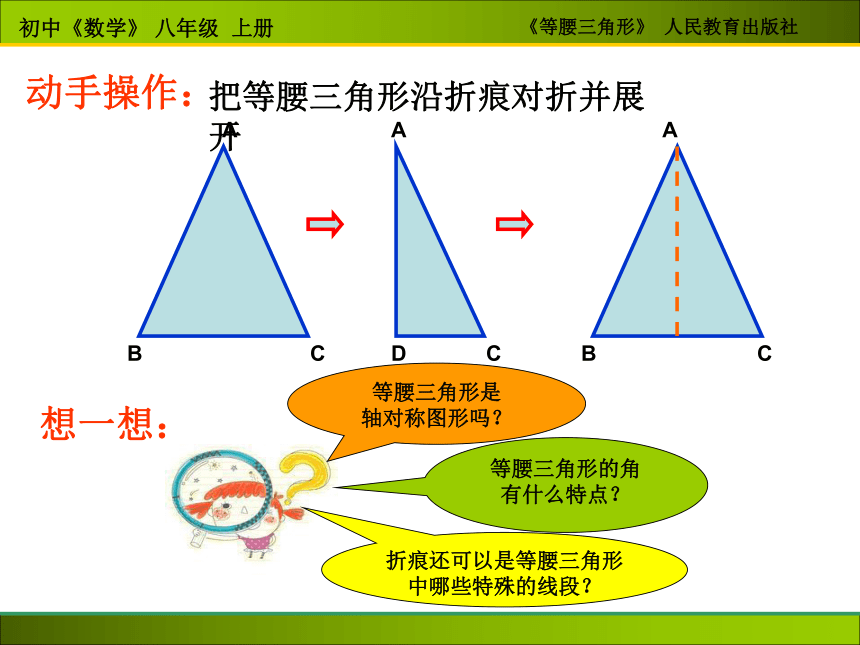
剪去阴影部分,再把它展开,得到的△ABC 有什么特点?探索并证明等腰三角形的性质 动手操作:把等腰三角形沿折痕对折并展开等腰三角形是
轴对称图形吗?等腰三角形的角
有什么特点?折痕还可以是等腰三角形中哪些特殊的线段?想一想:猜想:
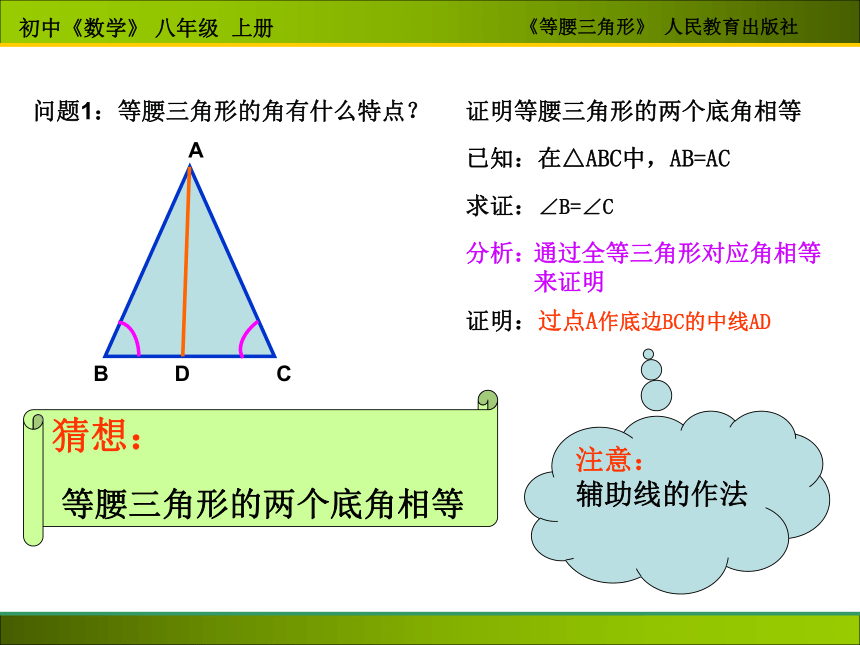
等腰三角形的两个底角相等证明等腰三角形的两个底角相等已知:在△ABC中,AB=AC求证:∠B=∠C分析:通过全等三角形对应角相等来证明证明:过点A作底边BC的中线AD问题1:等腰三角形的角有什么特点?D注意:
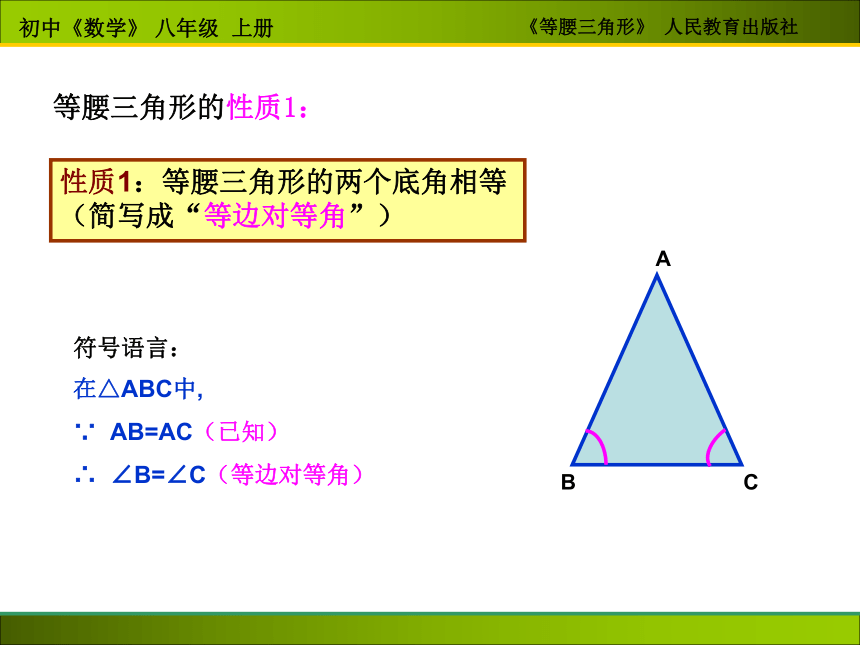
辅助线的作法等腰三角形的性质1:性质1:等腰三角形的两个底角相等 (简写成“等边对等角”)符号语言:在△ABC中,
∵ AB=AC(已知)
∴ ∠B=∠C(等边对等角)
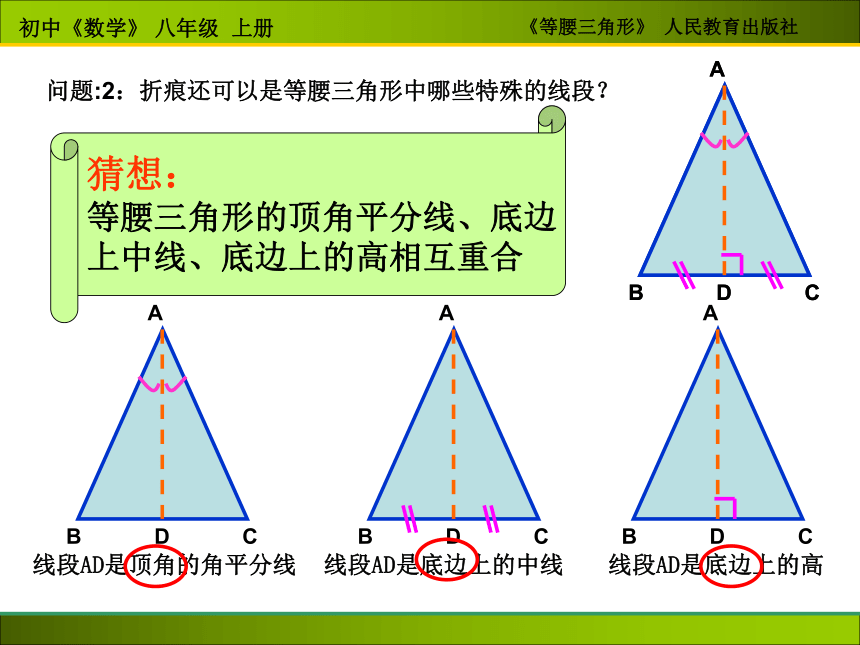
线段AD是顶角的角平分线线段AD是底边上的高线段AD是底边上的中线问题:2:折痕还可以是等腰三角形中哪些特殊的线段?猜想:
等腰三角形的顶角平分线、底边
上中线、底边上的高相互重合问题:2:折痕还可以是等腰三角形中哪些特殊的线段?猜想:
等腰三角形的顶角平分线、底边
上中线、底边上的高相互重合如何证明?等腰三角形的性质2:性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)符号语言:在△ABC中,
(1)∵ AB=AC,AB⊥AC ∴ ∠ =∠ , =
(2)∵ AB=AC,AD是中线 ∴ ∠ =∠ , ⊥
(3)∵ AB=AC,AD是角平分线 ∴ = , ⊥ 1212BDCDBDCDAD ADBCBC练习1:如图,在等腰△ABC中,AB=AC, ∠B=30°,
求∠A和∠C的度数。课堂练习 练习2:如图,在等腰△ABC中,AB=AC, ∠A=30°,
求∠B和∠C的度数。课堂练习 练习3:已知等腰三角形的一个内角为70°,则它的另外两个
内角的度数分别是多少度?课堂练习 例 题 如图,△ABC 中,AB =AC,点D 在AC 上,
且BD =BC =AD.求△ABC 各角的度数.xx2x2x2x课堂练习 如图,△ABC 是等腰直角三角形(AB =AC,∠BAC =90°),AD 是底边BC 上的高,标出∠B,∠C,∠BAD,∠DAC 的度数,并写出图中所有相等的线段.如图,△ABC 中,AB=AD=DC, ∠BAD= 26°.
求∠B和∠C 的度数.课堂练习 (1)本节课学习了哪些主要内容?
(2)我们是怎么探究等腰三角形的性质的?
(3)本节课你学到了哪些证明线段相等或角相等的
方法?课堂小结 课本P81第1题,P82第4题布置作业 谢 谢!
底边底角底角顶角有两条边相等的三角形叫做等腰三角形 如图所示,把一张长方形的纸按图中虚线对折,并
剪去阴影部分,再把它展开,得到的△ABC 有什么特点?探索并证明等腰三角形的性质 动手操作:把等腰三角形沿折痕对折并展开等腰三角形是
轴对称图形吗?等腰三角形的角
有什么特点?折痕还可以是等腰三角形中哪些特殊的线段?想一想:猜想:
等腰三角形的两个底角相等证明等腰三角形的两个底角相等已知:在△ABC中,AB=AC求证:∠B=∠C分析:通过全等三角形对应角相等来证明证明:过点A作底边BC的中线AD问题1:等腰三角形的角有什么特点?D注意:
辅助线的作法等腰三角形的性质1:性质1:等腰三角形的两个底角相等 (简写成“等边对等角”)符号语言:在△ABC中,
∵ AB=AC(已知)
∴ ∠B=∠C(等边对等角)
线段AD是顶角的角平分线线段AD是底边上的高线段AD是底边上的中线问题:2:折痕还可以是等腰三角形中哪些特殊的线段?猜想:
等腰三角形的顶角平分线、底边
上中线、底边上的高相互重合问题:2:折痕还可以是等腰三角形中哪些特殊的线段?猜想:
等腰三角形的顶角平分线、底边
上中线、底边上的高相互重合如何证明?等腰三角形的性质2:性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)符号语言:在△ABC中,
(1)∵ AB=AC,AB⊥AC ∴ ∠ =∠ , =
(2)∵ AB=AC,AD是中线 ∴ ∠ =∠ , ⊥
(3)∵ AB=AC,AD是角平分线 ∴ = , ⊥ 1212BDCDBDCDAD ADBCBC练习1:如图,在等腰△ABC中,AB=AC, ∠B=30°,
求∠A和∠C的度数。课堂练习 练习2:如图,在等腰△ABC中,AB=AC, ∠A=30°,
求∠B和∠C的度数。课堂练习 练习3:已知等腰三角形的一个内角为70°,则它的另外两个
内角的度数分别是多少度?课堂练习 例 题 如图,△ABC 中,AB =AC,点D 在AC 上,
且BD =BC =AD.求△ABC 各角的度数.xx2x2x2x课堂练习 如图,△ABC 是等腰直角三角形(AB =AC,∠BAC =90°),AD 是底边BC 上的高,标出∠B,∠C,∠BAD,∠DAC 的度数,并写出图中所有相等的线段.如图,△ABC 中,AB=AD=DC, ∠BAD= 26°.
求∠B和∠C 的度数.课堂练习 (1)本节课学习了哪些主要内容?
(2)我们是怎么探究等腰三角形的性质的?
(3)本节课你学到了哪些证明线段相等或角相等的
方法?课堂小结 课本P81第1题,P82第4题布置作业 谢 谢!
