八年级 第11讲 全等三角形[上学期]
文档属性
| 名称 | 八年级 第11讲 全等三角形[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 144.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-23 18:26:00 | ||
图片预览

文档简介
全等三角形
解题是一种实践性的技能,就像游泳、滑雪或弹钢琴一样,只能通过模仿、练习和钻研学到它―――玻利亚
[知识纵横]
全等三角形(congruent triangles)是平面几何内容的基础,这是因为全等三角形是研究特殊三角形、四边形等图形性质的有力工具,是解决与线段、角相关问题的一个出发点,运用全等三角形.可以证明线段相等、线段的和差倍分关系、角相等、两直线位置关系等常见的几何问题.
利用全等三角形证明问题.关键在于从复杂的图形中找到一对基础的三角形,这对基础的三角形从实质上来说,是由三角形全等判定定理中的一对三角形变位而来,也可能是由几对三角形组成,其间的关系互相传递,应熟悉涉及有公共边、公共角的以下两类基本图形:
【例1】 如图,给出下列结论:①;②BE=CF;③△ACN≌△ABM;④CD=DN,其中正确的结论是_______ (把你认为所有正确结论的序号填上). (广州市中考题)
思路点拨对一个复杂的图形,先找出比较明显的一对全等三角形,并发现有用的条件,进而判断推出其他三角形全等.
【例2】在△ABC中,AC=5,中线AD=4,则边AB的取值范围是( ).(连云港市中考题)
A.1思路点拨: 线段AC、AD、AB不是同一个三角形的三条边,通过中线倍长将分散的条件加以集中.
【例3】一张长方形纸片沿对角线剪开,得到两张三角形纸片,再将这两张三角形纸片摆成如下右图形式,使点B、F、C、D在同一条直线上. (2005年江西省中考题)
(1)求证:AB⊥ED;
(2)若.PB=BC,请找出图中与此条件有关的一对全等三角形,并给予证明.
思路点拨本例是一道拼图开放题.对于(2),由PB=BC,寻找对应三角形,由此可证明多对全等三角形.
【例4】若两个三角形的两边和其中一边上的高分别对应相等,试判断这两个三角形的第三边所对的角之间的关系,并说明理由.(第9届“五羊杯”竞赛题改编题)
思路点拨 运用全等三角形的判定和性质,探讨两角之间的关系,解题的关键是由高的特殊性.分三角形的形状讨论.
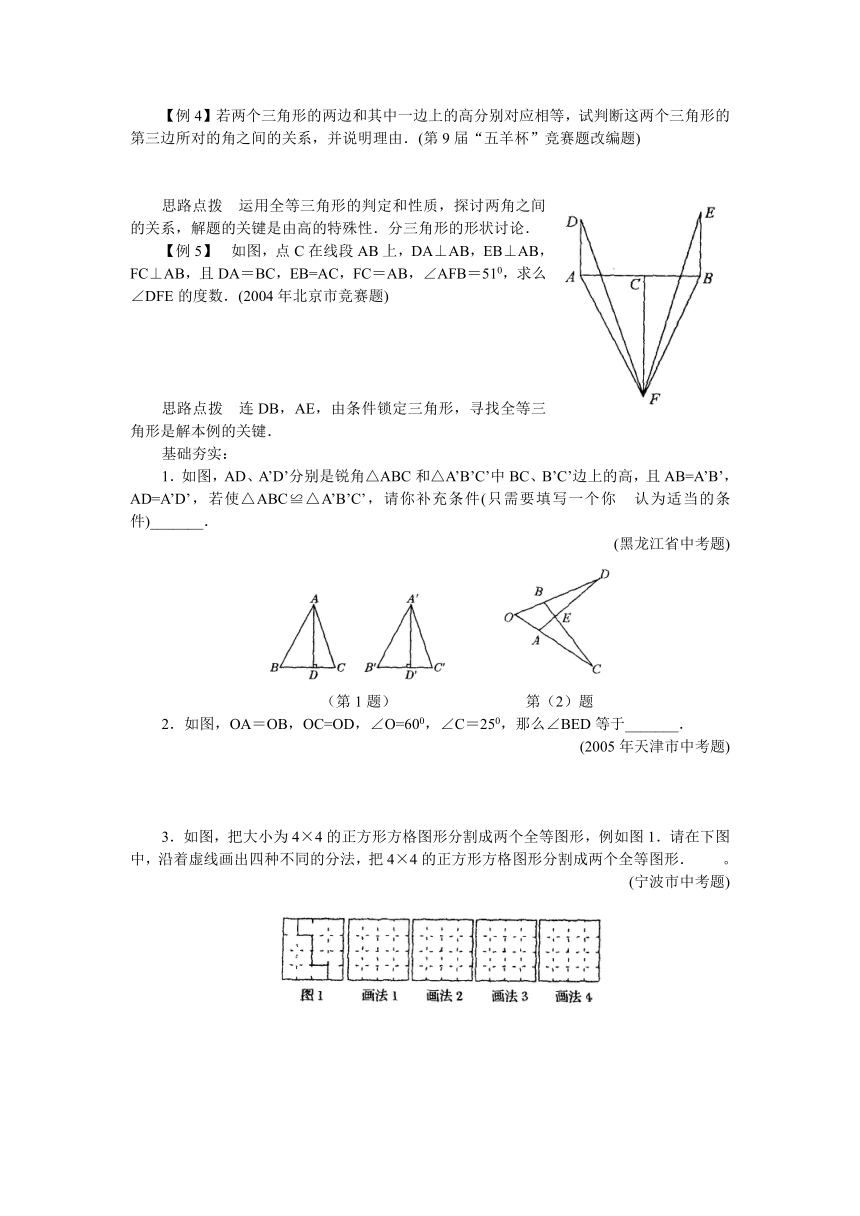
【例5】 如图,点C在线段AB上,DA⊥AB,EB⊥AB,FC⊥AB,且DA=BC,EB=AC,FC=AB,∠AFB=510,求么∠DFE的度数.(2004年北京市竞赛题)
思路点拨 连DB,AE,由条件锁定三角形,寻找全等三角形是解本例的关键.
基础夯实:
1.如图,AD、A’D’分别是锐角△ABC和△A’B’C’中BC、B’C’边上的高,且AB=A’B’,AD=A’D’,若使△ABC≌△A’B’C’,请你补充条件(只需要填写一个你 认为适当的条件)_______.
(黑龙江省中考题)
(第1题) 第(2)题
2.如图,OA=OB,OC=OD,∠O=600,∠C=250,那么∠BED等于_______.
(2005年天津市中考题)
3.如图,把大小为4×4的正方形方格图形分割成两个全等图形,例如图1.请在下图中,沿着虚线画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形. 。
(宁波市中考题)
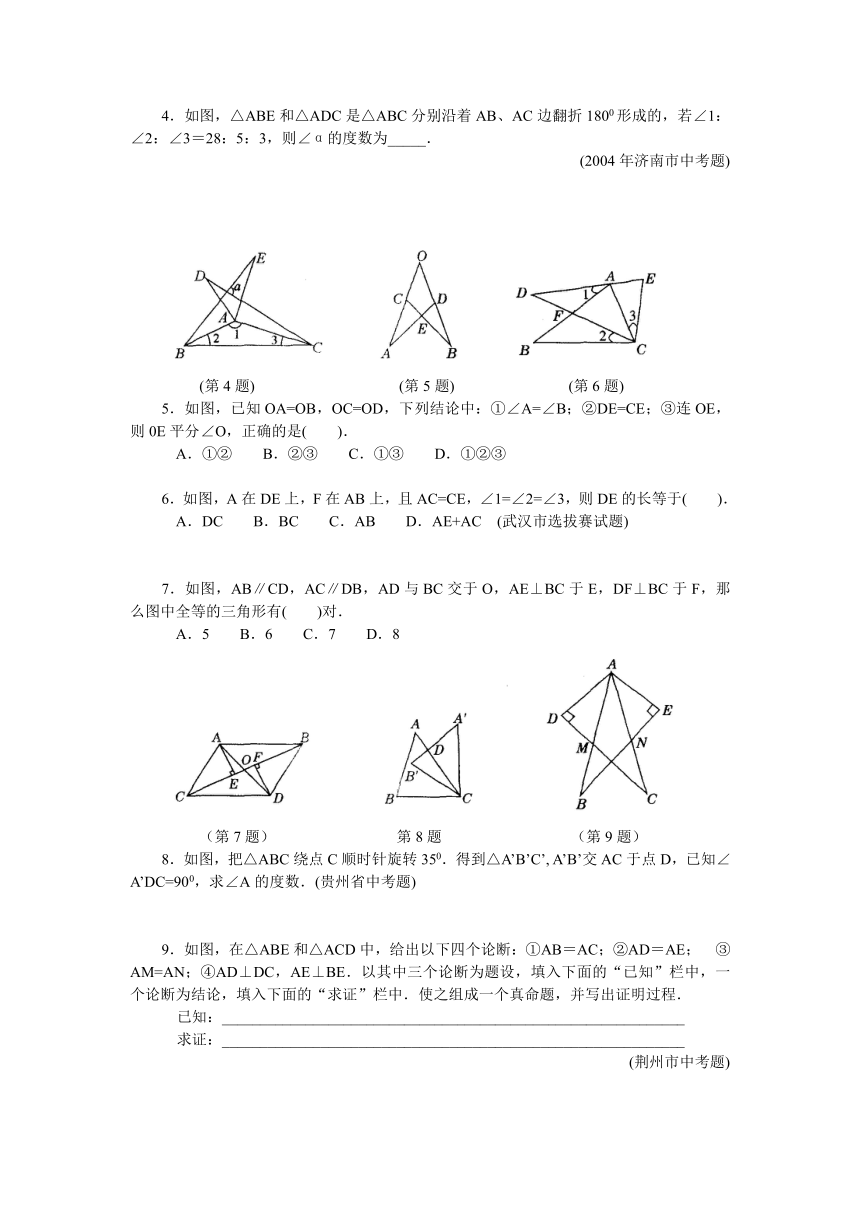
4.如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折1800形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为_____.
(2004年济南市中考题)
(第4题) (第5题) (第6题)
5.如图,已知OA=OB,OC=OD,下列结论中:①∠A=∠B;②DE=CE;③连OE,则0E平分∠O,正确的是( ).
A.①② B.②③ C.①③ D.①②③
6.如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于( ).
A.DC B.BC C.AB D.AE+AC (武汉市选拔赛试题)
7.如图,AB∥CD,AC∥DB,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )对.
A.5 B.6 C.7 D.8
(第7题) 第8题 (第9题)
8.如图,把△ABC绕点C顺时针旋转350.得到△A’B’C’, A’B’交AC于点D,已知∠A’DC=900,求∠A的度数.(贵州省中考题)
9.如图,在△ABE和△ACD中,给出以下四个论断:①AB=AC;②AD=AE; ③AM=AN;④AD⊥DC,AE⊥BE.以其中三个论断为题设,填入下面的“已知”栏中,一个论断为结论,填入下面的“求证”栏中.使之组成一个真命题,并写出证明过程.
已知:_____________________________________________________________
求证:_____________________________________________________________
(荆州市中考题)
10.在△ABC中,∠ACB=900,AC=BC,直线MN经过点C,且AD⊥MN于D,BE ⊥ MN于E.
(1)当直线MN绕点C旋转到图①的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图②的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图③的位置时,试问:DE、AD、BE有怎样的等量关系 请写出这个等量关系,并加以证明.
(2004年海口市中考题)
能力拓展:
11.在△ABC中,高AD和BE交于H点,且BH=AC,则∠ABC=_____。
12.如图,已知AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=360, 那么∠BED=_______. (河南省竞赛题)
13.如图,D是△ABC的边AB上一点,DF交AC于点E,给出三个论断:①DE=FE;②AE=CE;③FC∥AB,以其中一个论断为结论,其余两个论断为条件,可作出三个命题,其中正确命题的个数是__________.(武汉市选拔赛试题)
14。如图,在△ABC中,AD为BC边上的中线,若AB=5,AC=3,则AD的范围是______.
15.如图,在△ABC中,AC=BC,∠ACB=900.AD平分∠BAC,BE⊥AD交AC 的延长线于F,E为垂足.则结沦:①AD=BF;②CF=CD;③AC+CD=AB; ④BE=CF;⑤BF=2BE,其中正确结论的个数是( ).(2005年河北省竞赛题)
A.1 B.2 C.3 D.4
16.如图,在四边形ABCD中.对角线AC平分∠BAD,AB>AD,下列结论中正确的是( ).
A.AB-AD>CB—CD B.AB—AD=CB—CD
C.AB-AD<CB—CD D.AB—AD与CB-CD的大小关系不确定.
(第17届江苏省竞赛题)
17.考查下列命题:①全等三角形的对应边上的中线、高、角平分线对应相等;②两边和其中一边上的中线(或第三边上的中线)对应相等的两个三角形全等; ③两角和其中一角的角平分线(或第三角的角平分线)对应相等的两个三角形全等;④两边和其中一边上的高(或第三边上的高)对应相等的两个三角形全等.
其中正确命题的个数有( ).
A.4个 B.3个 C.2个 D.1个
18.如图,在四边形ABCD中.AC平分∠BAD,过C作CE⊥AB于E,并且AE=(AB+AD),求∠ABC十∠ADC的度数. (上海市竞赛题)
19.如图,△ABC中,D是BC的中点.DE⊥DF.试判断BE+CF与EF的大小关系,并证明你的结论.
20.如图,已知AB=CD=AE=BC+DE=2,∠ABC=∠AED===900,求五边形 ABCDE的面积. (第1 7届江苏省竞赛题)
综合创新
21.如图,在△ABC中,∠ABC=600,AD、CE分别平分∠BAC、∠ACB,求证:AC=AE+CD.
(武汉市选拔赛试题)
22.如图:已知∠ABC=∠DBE=900,DB=BE,AB=BC.
(1)求证:AD=CE,AD⊥CE:
(2)若△DBE绕点B旋转到△ABC外部,其他条件不变,则(1)中结论是否仍成立 请证明.
解题是一种实践性的技能,就像游泳、滑雪或弹钢琴一样,只能通过模仿、练习和钻研学到它―――玻利亚
[知识纵横]
全等三角形(congruent triangles)是平面几何内容的基础,这是因为全等三角形是研究特殊三角形、四边形等图形性质的有力工具,是解决与线段、角相关问题的一个出发点,运用全等三角形.可以证明线段相等、线段的和差倍分关系、角相等、两直线位置关系等常见的几何问题.
利用全等三角形证明问题.关键在于从复杂的图形中找到一对基础的三角形,这对基础的三角形从实质上来说,是由三角形全等判定定理中的一对三角形变位而来,也可能是由几对三角形组成,其间的关系互相传递,应熟悉涉及有公共边、公共角的以下两类基本图形:
【例1】 如图,给出下列结论:①;②BE=CF;③△ACN≌△ABM;④CD=DN,其中正确的结论是_______ (把你认为所有正确结论的序号填上). (广州市中考题)
思路点拨对一个复杂的图形,先找出比较明显的一对全等三角形,并发现有用的条件,进而判断推出其他三角形全等.
【例2】在△ABC中,AC=5,中线AD=4,则边AB的取值范围是( ).(连云港市中考题)
A.1
【例3】一张长方形纸片沿对角线剪开,得到两张三角形纸片,再将这两张三角形纸片摆成如下右图形式,使点B、F、C、D在同一条直线上. (2005年江西省中考题)
(1)求证:AB⊥ED;
(2)若.PB=BC,请找出图中与此条件有关的一对全等三角形,并给予证明.
思路点拨本例是一道拼图开放题.对于(2),由PB=BC,寻找对应三角形,由此可证明多对全等三角形.
【例4】若两个三角形的两边和其中一边上的高分别对应相等,试判断这两个三角形的第三边所对的角之间的关系,并说明理由.(第9届“五羊杯”竞赛题改编题)
思路点拨 运用全等三角形的判定和性质,探讨两角之间的关系,解题的关键是由高的特殊性.分三角形的形状讨论.
【例5】 如图,点C在线段AB上,DA⊥AB,EB⊥AB,FC⊥AB,且DA=BC,EB=AC,FC=AB,∠AFB=510,求么∠DFE的度数.(2004年北京市竞赛题)
思路点拨 连DB,AE,由条件锁定三角形,寻找全等三角形是解本例的关键.
基础夯实:
1.如图,AD、A’D’分别是锐角△ABC和△A’B’C’中BC、B’C’边上的高,且AB=A’B’,AD=A’D’,若使△ABC≌△A’B’C’,请你补充条件(只需要填写一个你 认为适当的条件)_______.
(黑龙江省中考题)
(第1题) 第(2)题
2.如图,OA=OB,OC=OD,∠O=600,∠C=250,那么∠BED等于_______.
(2005年天津市中考题)
3.如图,把大小为4×4的正方形方格图形分割成两个全等图形,例如图1.请在下图中,沿着虚线画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形. 。
(宁波市中考题)
4.如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折1800形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为_____.
(2004年济南市中考题)
(第4题) (第5题) (第6题)
5.如图,已知OA=OB,OC=OD,下列结论中:①∠A=∠B;②DE=CE;③连OE,则0E平分∠O,正确的是( ).
A.①② B.②③ C.①③ D.①②③
6.如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于( ).
A.DC B.BC C.AB D.AE+AC (武汉市选拔赛试题)
7.如图,AB∥CD,AC∥DB,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )对.
A.5 B.6 C.7 D.8
(第7题) 第8题 (第9题)
8.如图,把△ABC绕点C顺时针旋转350.得到△A’B’C’, A’B’交AC于点D,已知∠A’DC=900,求∠A的度数.(贵州省中考题)
9.如图,在△ABE和△ACD中,给出以下四个论断:①AB=AC;②AD=AE; ③AM=AN;④AD⊥DC,AE⊥BE.以其中三个论断为题设,填入下面的“已知”栏中,一个论断为结论,填入下面的“求证”栏中.使之组成一个真命题,并写出证明过程.
已知:_____________________________________________________________
求证:_____________________________________________________________
(荆州市中考题)
10.在△ABC中,∠ACB=900,AC=BC,直线MN经过点C,且AD⊥MN于D,BE ⊥ MN于E.
(1)当直线MN绕点C旋转到图①的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图②的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图③的位置时,试问:DE、AD、BE有怎样的等量关系 请写出这个等量关系,并加以证明.
(2004年海口市中考题)
能力拓展:
11.在△ABC中,高AD和BE交于H点,且BH=AC,则∠ABC=_____。
12.如图,已知AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=360, 那么∠BED=_______. (河南省竞赛题)
13.如图,D是△ABC的边AB上一点,DF交AC于点E,给出三个论断:①DE=FE;②AE=CE;③FC∥AB,以其中一个论断为结论,其余两个论断为条件,可作出三个命题,其中正确命题的个数是__________.(武汉市选拔赛试题)
14。如图,在△ABC中,AD为BC边上的中线,若AB=5,AC=3,则AD的范围是______.
15.如图,在△ABC中,AC=BC,∠ACB=900.AD平分∠BAC,BE⊥AD交AC 的延长线于F,E为垂足.则结沦:①AD=BF;②CF=CD;③AC+CD=AB; ④BE=CF;⑤BF=2BE,其中正确结论的个数是( ).(2005年河北省竞赛题)
A.1 B.2 C.3 D.4
16.如图,在四边形ABCD中.对角线AC平分∠BAD,AB>AD,下列结论中正确的是( ).
A.AB-AD>CB—CD B.AB—AD=CB—CD
C.AB-AD<CB—CD D.AB—AD与CB-CD的大小关系不确定.
(第17届江苏省竞赛题)
17.考查下列命题:①全等三角形的对应边上的中线、高、角平分线对应相等;②两边和其中一边上的中线(或第三边上的中线)对应相等的两个三角形全等; ③两角和其中一角的角平分线(或第三角的角平分线)对应相等的两个三角形全等;④两边和其中一边上的高(或第三边上的高)对应相等的两个三角形全等.
其中正确命题的个数有( ).
A.4个 B.3个 C.2个 D.1个
18.如图,在四边形ABCD中.AC平分∠BAD,过C作CE⊥AB于E,并且AE=(AB+AD),求∠ABC十∠ADC的度数. (上海市竞赛题)
19.如图,△ABC中,D是BC的中点.DE⊥DF.试判断BE+CF与EF的大小关系,并证明你的结论.
20.如图,已知AB=CD=AE=BC+DE=2,∠ABC=∠AED===900,求五边形 ABCDE的面积. (第1 7届江苏省竞赛题)
综合创新
21.如图,在△ABC中,∠ABC=600,AD、CE分别平分∠BAC、∠ACB,求证:AC=AE+CD.
(武汉市选拔赛试题)
22.如图:已知∠ABC=∠DBE=900,DB=BE,AB=BC.
(1)求证:AD=CE,AD⊥CE:
(2)若△DBE绕点B旋转到△ABC外部,其他条件不变,则(1)中结论是否仍成立 请证明.
