人教版数学七年级上册 第四章 几何图形初步 单元测试(含答案)
文档属性
| 名称 | 人教版数学七年级上册 第四章 几何图形初步 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 141.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 07:36:27 | ||
图片预览




文档简介
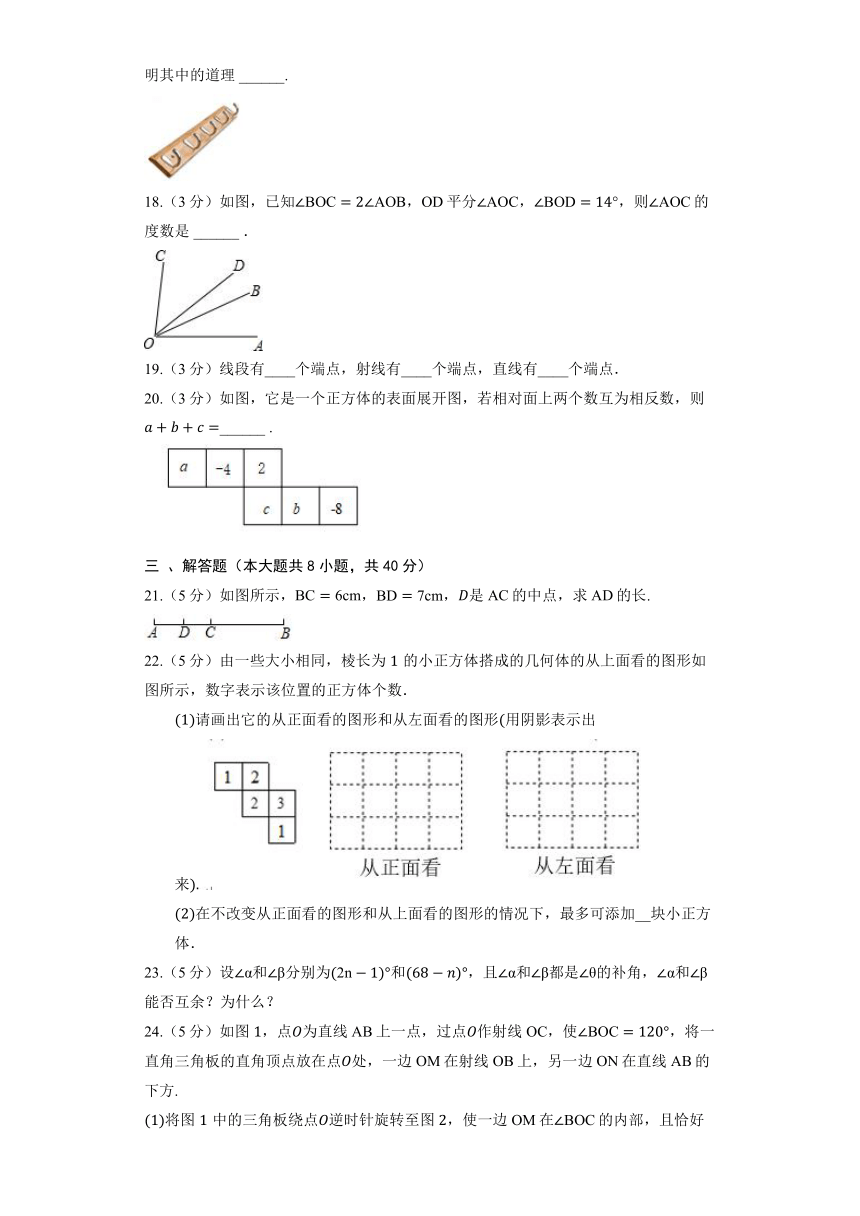
人教版数学七年级上册《第四章 几何图形初步》单元测试
一 、单选题(本大题共15小题,共45分)
1.(3分)下列说法正确的是( )
A. 延长直线AB B. 延长射线AB C. 延长线段AB D. 画直线AB=4cm
2.(3分)如图图形不能围成正方体的是
A. B.
C. D.
3.(3分)一条直线上有8个点,则以这8个点为端点的线段共有( )
A. 7条 B. 14条 C. 16条 D. 28条
4.(3分)两根木条,一根长,一根长,将它们的一个端点重合,放在同一条直线上,此时两根木条中点间的距离
A. B. C. D. 或
5.(3分)如图,下列四种物体中,哪种物体最接近于圆柱
A. B. C. D.
6.(3分)已知,则的补角等于
A. B. C. D.
7.(3分)如图中有( )条线段.
A. 3 B. 4 C. 5 D. 6
8.(3分)如图,直角三角形绕直线旋转一周,得到的立体图形是
A. B. C. D.
9.(3分)萌萌从学校点出发,沿北偏西走了米到达图书馆点,新新也从学校点出发,沿南偏西方向走了米到达科技馆点,则的度数为
A. B. C. D.
10.(3分)下列说法正确的是
A. 两点确定一条直线 B. 两条射线组成的图形叫作角
C. 两点之间直线最短 D. 若,则点为的中点
11.(3分)一个角的余角是这个角的补角的,则这个角的度数是( )
A. B. C. D.
12.(3分)已知:,,,则下列说法正确的是
A. B.
C. D. 、、互不相等
13.(3分) ,是线段上顺次两点,,分别是,中点,若则的长为
A. B.
C. D.
14.(3分)如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“负”相对的面上的汉字是
A. 强 B. 课 C. 提 D. 质
15.(3分)如图,是线段的中点,是上一点,则下列结论中错误的是
A. B.
C. D.
二 、填空题(本大题共5小题,共15分)
16.(3分)时钟在点半时,时针与分针的夹角为______度.
17.(3分)在日常生活和生产中有很多现象可以用数学知识进行解释.如图,要把一根挂衣帽的挂钩架水平固定在墙上,至少需要钉 ______个钉子.用你所学数学知识说明其中的道理 ______.
18.(3分)如图,已知,平分,,则的度数是 ______ .
19.(3分)线段有____个端点,射线有____个端点,直线有____个端点.
20.(3分)如图,它是一个正方体的表面展开图,若相对面上两个数互为相反数,则______ .
三 、解答题(本大题共8小题,共40分)
21.(5分)如图所示,,,是的中点,求的长.
22.(5分)由一些大小相同,棱长为的小正方体搭成的几何体的从上面看的图形如图所示,数字表示该位置的正方体个数.
请画出它的从正面看的图形和从左面看的图形用阴影表示出来
在不改变从正面看的图形和从上面看的图形的情况下,最多可添加__块小正方体.
23.(5分)设和分别为和,且和都是的补角,和能否互余?为什么?
24.(5分)如图,点为直线上一点,过点作射线,使,将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的下方.
将图中的三角板绕点逆时针旋转至图,使一边在的内部,且恰好平分,问:直线是否平分?请直接写出结论:直线______ 平分或不平分
将图中的三角板绕点按每秒的速度沿逆时针方向旋转一周,在旋转的过程中,第秒时,直线恰好平分锐角,则的值为 ______ 直接写出结果
将图中的三角板绕点顺时针旋转,请探究,当始终在的内部时如图,与的差是否发生变化?若不变,请求出这个差值;若变化,请举例说明.
25.(5分)如图所示,点在线段的延长线上,且,是的中点,若,求的长.
解:,,
______ ______
是的中点,
______ ______
______ ______
26.(5分)已知一个角的补角是这个角的余角的倍,求这个角.
27.(5分)如图,已知线段.
延长线段到,使,为的中点,请准确画出图形并标出点.
若,求的长.
28.(5分)(1)如图,用绿色笔画出直线AB,再用棕色笔画出线段BA,最后用红笔画出线段AB.想一想:线段BA与线段AB是同一条线段吗?
(2)如图,点A、B、C、D在一条直线上.用绿色笔画出射线AB,再用棕色笔画出射线BA,最后分别用蓝笔和红笔画出射线BC和射线DC.理解射线AB与射线BA为什么不是同一射线,而射线BA与射线BC却是同一条射线.想一想:射线BC与射线DC是同一条射线吗?
答案和解析
1.【答案】C;
【解析】直线没有端点,两边是无限长的,故A、D项错误;射线有一端点,但也是无限长的,故B项错误;线段为有限长,且有两端点,故可延长,故C项正确。
故本题正确答案为C。
2.【答案】B;
【解析】解:所有选项中只有选项出现“凹”字状,所以不能组成正方体,而,,选项中,能围成正方体.
故选:.
依据正方体的展开图的特征,当六个正方形出现“田”字,“凹”字状时,不能围成正方体.
这道题主要考查了展开图折叠成几何体,解题时注意:当六个正方形组成“田”字,“凹”字状时,不能折成正方体.
3.【答案】D;
【解析】
(条).
答:以这8个点为端点的线段共有28条.
故选:D.
4.【答案】D;
【解析】解:如图,设较长的木条为,较短的木条为,
、分别为、的中点,
,
,
①如图,不在上时,,
②如图,在上时,,
综上所述,两根木条的中点间的距离是或
故选:
设较长的木条为,较短的木条为,根据中点定义求出、的长度,然后分①不在上时,,②在上时,,分别代入数据进行计算即可得解.
此题主要考查了两点间的距离,主要利用了线段的中点定义,难点在于要分情况讨论,作出图形更形象直观.
5.【答案】A;
【解析】
该题考查立体图形圆柱的认识.圆柱是由两个平行的平面和一个曲面构成,且曲面垂直平面.根据圆柱定义逐项判定即可.
解:生日蛋糕是圆柱,故A正确;
B.弯管的曲面与平面不垂直不是圆柱,故B错误;
C.烟囱是圆台不是圆柱,故C错误;
D.酒瓶是圆柱与圆台组合,故D错误.
故选A.
6.【答案】B;
【解析】解:的补角
故选:
根据补角的定义求解即可.
此题主要考查的是补角的定义,掌握补角的定义是解答该题的关键.
7.【答案】D;
【解析】解:图中线段有:AD、AC、AB、DC、DB、CB,共6条.
故选D.
8.【答案】C;
【解析】
该题考查了点、线、面、体,重在体现面动成体:考查学生立体图形的空间想象能力及分析问题,解决问题的能力.解答该题的关键在于根据题意想象立体图形逐项分析即可得到答案.
解:是由半圆沿直径旋转得到的,此选项错误;
B.是由直角梯形沿直角腰旋转得到的,此选项错误;
C.是由直角三角形沿直角边旋转得到的,此选项正确;
D.是由长方形沿一边旋转得到的,此选项错误.
故选C.
9.【答案】D;
【解析】解:如图所示:
所以:,
故选:
根据题目已知画出图形,准确找到方位角即可.
此题主要考查了方位角,根据题意画出图形是解答该题的关键.
10.【答案】A;
【解析】
该题考查了线段的性质,直线的性质,以及角的定义,是基础题,熟记概念与各性质是解答该题的关键.
根据两点确定一条直线,角的定义,线段中点的定义对各选项分析判断后利用排除法求解.
解:、两点确定一条直线正确,故本选项正确;
B、应为有公共端点的两条射线组成的图形叫做角,故本选项错误;
C、应为两点之间线段最短,故本选项错误;
D、若,则点为的中点错误,因为、、三点不一定共线,故本选项错误.
故选A.
11.【答案】B;
【解析】略
12.【答案】C;
【解析】该题考查角的大小比较和度分秒之间的换算,在比较角的大小时有时可把度化为分来进行比较,首先同一单位,利用,把,,把度化为分,再进一步与比较得出答案即可.解:,,.故选C.
13.【答案】A;
【解析】解:是的中点,是的中点
,
,
.
故选A.
由是的中点,是的中点,则,,故AB可求.
考查了两点间的距离,首先根据线段的中点概念,写出需要的关系式.再根据题意,结合图形进行线段的和与差的计算.
14.【答案】B;
【解析】解:这是一个正方体的平面展开图,共有六个面,其中面“强”与面“提”相对,面“减”与面“质”相对,面“负”与面“课”相对.
故选:
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
此题主要考查了正方体相对两个面上的文字,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念是解决此类问题的关键.
15.【答案】C;
【解析】【试题解析】
这道题主要考查线段中点的定义和等量代换,只要细心进行线段的代换便不难得到正确答案.
根据和两种情况和对各选项分析后即不难选出答案.
解:是线段的中点,
,
A.,故本选项正确;
B.,故本选项正确;
C.,故本选项错误;
D.,故本选项正确.
故选C.
16.【答案】;
【解析】解:点半时,时针和分针中间相差个大格.
钟表个数字,每相邻两个数字之间的夹角为,
点半时分针与时针的夹角是.
画出草图,利用钟表表盘的特征解答.
用到的知识点为:钟表上个数字,每相邻两个数字之间的夹角为.
17.【答案】两 两点确定一条直线;
【解析】解:要把一根细木条固定在墙上,至少需要钉两个钉子,其中蕴含的数学道理是两点确定一条直线,
故答案为:两,两点确定一条直线.
根据直线的性质,可得答案.
此题主要考查了直线的性质,熟记直线的性质是解题关键.
18.【答案】84°;
【解析】解:设,则,
又平分,
,
,
,
即,
故答案为:.
此题可以设,,再进一步表示,根据角平分线的概念表示,最后根据已知角的度数列方程即可计算.
该题考查了角平分线的定义.此类题设恰当的未知数,根据已知条件进一步表示出相关的角,列方程计算较为简便.
19.【答案】2;1;0;
【解析】【略】。
20.【答案】10;
【解析】解:根据“相间、端是对面”可知:
的相对面是,则
的对立面是,则
的对立面是,则
所以
故答案是:
根据正方体展开图的特征,判断“对面”求出、、,再计算即可.
此题主要考查了相反数,正方体相对两个面上的文字,对于此类问题一般方法是用纸按图的样子折叠后可以解决,或是在对展开图理解的基础上直接想象.
21.【答案】解:∵BC=6cm,BD=7cm,
∴CD=BD-BC=1cm;
∵点D是AC的中点,
∴AD=CD=1cm.;
【解析】
由点是的中点,于是得到,根据线段的和差即可得到结论.
此题主要考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答该题的关键.
22.【答案】解:如图所示:
.;
【解析】【试题解析】
该题考查认识立体图形,掌握好从几个方向看立体图形所得图形的特点是解题关键.
由已知条件可知,从正面看的图形有列,每列小正方数形数目分别为,,;从左面看的图形有列,每列小正方数形数目分别为,,,据此可画出图形.
解:见答案;
在不改变从正面看的图形和上面看的图形的情况下,最多可添加个小正方体,
故答案为:.
23.【答案】解:由∠α、∠β都是∠θ的补角,得
∠α=∠β,即2n-1=68-n.
解得n=23;
∠α与∠β互余,理由如下:
∵∠α和∠β分别为(2n-1)°和(68-n)°,
∴∠α=(2n-1)°=45°,∠β=(68-n)°=45°,
∵∠α+∠β=90°,
∴∠α与∠β互为余角.;
【解析】
先根据补角的性质,可得,解这个方程,可得的值;根据余角的定义,可得答案.
此题主要考查了余角和补角.解答该题的关键是掌握余角和补角有关定义和性质.
24.【答案】平分 10或40;
【解析】解:直线平分
理由如下:
设的反向延长线为,
平分,,
,
又,
,
,
,
平分,
即直线平分,
故答案为:平分;
,
即旋转或时直线平分
由题意得,或
解得:或,
故答案为:或;
的差不变.
,,
、
与的差不变,这个差值是
设的反向延长线为,由角平分线的性质和对顶角的性质可求得;
由直线恰好平分锐角可知旋转或时直线平分,根据旋转速度可求得需要的时间;
由,,可知、,最后求得两角的差,从而可做出判断.
此题主要考查的是角的计算、角平分线的定义,用含的式子表示出和的长是解答该题的关键.
25.【答案】BC;6;AC;3;AB;1;
【解析】解:,,
,
,
为中点,
,
,
故答案为:,,,,,
求出长,根据线段中点求出,代入求出即可.
此题主要考查了线段中点和求两点间的距离的应用,关键是求出、长和得出
26.【答案】解:设这个角为x,则补角为(180°-x),余角为(90°-x),
由题意得,3(90°-x)=180°-x,
解得:x=45,
即这个角为45°.;
【解析】
根据互余的两角之和为,互补的两角之和为,表示出余角和补角,然后列方程求解即可.
该题考查了余角和补角的知识,属于基础题,关键是掌握互余的两角之和为,互补的两角之和为.
27.【答案】解:根据题意,画出的图形如图所示:;
是的中点,,
,
,
,
.;
【解析】该题考查的是两点间的距离,画线段以及中点的性质.
根据题意画出线段,利用中点的性质标出点即可;
由的长结合中点的性质得到的长,再根据线段和差的性质即可得到的长.
28.【答案】解:(1)根据图形可得线段BA与线段AB是同一条线段;
(2)由题意得:射线BC与射线DC的顶点不同,故不是同一条射线.;
【解析】(1)根据线段的定义及特点可得两者是同一条线段.
(2)根据射线的概念可判断出答案.
一 、单选题(本大题共15小题,共45分)
1.(3分)下列说法正确的是( )
A. 延长直线AB B. 延长射线AB C. 延长线段AB D. 画直线AB=4cm
2.(3分)如图图形不能围成正方体的是
A. B.
C. D.
3.(3分)一条直线上有8个点,则以这8个点为端点的线段共有( )
A. 7条 B. 14条 C. 16条 D. 28条
4.(3分)两根木条,一根长,一根长,将它们的一个端点重合,放在同一条直线上,此时两根木条中点间的距离
A. B. C. D. 或
5.(3分)如图,下列四种物体中,哪种物体最接近于圆柱
A. B. C. D.
6.(3分)已知,则的补角等于
A. B. C. D.
7.(3分)如图中有( )条线段.
A. 3 B. 4 C. 5 D. 6
8.(3分)如图,直角三角形绕直线旋转一周,得到的立体图形是
A. B. C. D.
9.(3分)萌萌从学校点出发,沿北偏西走了米到达图书馆点,新新也从学校点出发,沿南偏西方向走了米到达科技馆点,则的度数为
A. B. C. D.
10.(3分)下列说法正确的是
A. 两点确定一条直线 B. 两条射线组成的图形叫作角
C. 两点之间直线最短 D. 若,则点为的中点
11.(3分)一个角的余角是这个角的补角的,则这个角的度数是( )
A. B. C. D.
12.(3分)已知:,,,则下列说法正确的是
A. B.
C. D. 、、互不相等
13.(3分) ,是线段上顺次两点,,分别是,中点,若则的长为
A. B.
C. D.
14.(3分)如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“负”相对的面上的汉字是
A. 强 B. 课 C. 提 D. 质
15.(3分)如图,是线段的中点,是上一点,则下列结论中错误的是
A. B.
C. D.
二 、填空题(本大题共5小题,共15分)
16.(3分)时钟在点半时,时针与分针的夹角为______度.
17.(3分)在日常生活和生产中有很多现象可以用数学知识进行解释.如图,要把一根挂衣帽的挂钩架水平固定在墙上,至少需要钉 ______个钉子.用你所学数学知识说明其中的道理 ______.
18.(3分)如图,已知,平分,,则的度数是 ______ .
19.(3分)线段有____个端点,射线有____个端点,直线有____个端点.
20.(3分)如图,它是一个正方体的表面展开图,若相对面上两个数互为相反数,则______ .
三 、解答题(本大题共8小题,共40分)
21.(5分)如图所示,,,是的中点,求的长.
22.(5分)由一些大小相同,棱长为的小正方体搭成的几何体的从上面看的图形如图所示,数字表示该位置的正方体个数.
请画出它的从正面看的图形和从左面看的图形用阴影表示出来
在不改变从正面看的图形和从上面看的图形的情况下,最多可添加__块小正方体.
23.(5分)设和分别为和,且和都是的补角,和能否互余?为什么?
24.(5分)如图,点为直线上一点,过点作射线,使,将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的下方.
将图中的三角板绕点逆时针旋转至图,使一边在的内部,且恰好平分,问:直线是否平分?请直接写出结论:直线______ 平分或不平分
将图中的三角板绕点按每秒的速度沿逆时针方向旋转一周,在旋转的过程中,第秒时,直线恰好平分锐角,则的值为 ______ 直接写出结果
将图中的三角板绕点顺时针旋转,请探究,当始终在的内部时如图,与的差是否发生变化?若不变,请求出这个差值;若变化,请举例说明.
25.(5分)如图所示,点在线段的延长线上,且,是的中点,若,求的长.
解:,,
______ ______
是的中点,
______ ______
______ ______
26.(5分)已知一个角的补角是这个角的余角的倍,求这个角.
27.(5分)如图,已知线段.
延长线段到,使,为的中点,请准确画出图形并标出点.
若,求的长.
28.(5分)(1)如图,用绿色笔画出直线AB,再用棕色笔画出线段BA,最后用红笔画出线段AB.想一想:线段BA与线段AB是同一条线段吗?
(2)如图,点A、B、C、D在一条直线上.用绿色笔画出射线AB,再用棕色笔画出射线BA,最后分别用蓝笔和红笔画出射线BC和射线DC.理解射线AB与射线BA为什么不是同一射线,而射线BA与射线BC却是同一条射线.想一想:射线BC与射线DC是同一条射线吗?
答案和解析
1.【答案】C;
【解析】直线没有端点,两边是无限长的,故A、D项错误;射线有一端点,但也是无限长的,故B项错误;线段为有限长,且有两端点,故可延长,故C项正确。
故本题正确答案为C。
2.【答案】B;
【解析】解:所有选项中只有选项出现“凹”字状,所以不能组成正方体,而,,选项中,能围成正方体.
故选:.
依据正方体的展开图的特征,当六个正方形出现“田”字,“凹”字状时,不能围成正方体.
这道题主要考查了展开图折叠成几何体,解题时注意:当六个正方形组成“田”字,“凹”字状时,不能折成正方体.
3.【答案】D;
【解析】
(条).
答:以这8个点为端点的线段共有28条.
故选:D.
4.【答案】D;
【解析】解:如图,设较长的木条为,较短的木条为,
、分别为、的中点,
,
,
①如图,不在上时,,
②如图,在上时,,
综上所述,两根木条的中点间的距离是或
故选:
设较长的木条为,较短的木条为,根据中点定义求出、的长度,然后分①不在上时,,②在上时,,分别代入数据进行计算即可得解.
此题主要考查了两点间的距离,主要利用了线段的中点定义,难点在于要分情况讨论,作出图形更形象直观.
5.【答案】A;
【解析】
该题考查立体图形圆柱的认识.圆柱是由两个平行的平面和一个曲面构成,且曲面垂直平面.根据圆柱定义逐项判定即可.
解:生日蛋糕是圆柱,故A正确;
B.弯管的曲面与平面不垂直不是圆柱,故B错误;
C.烟囱是圆台不是圆柱,故C错误;
D.酒瓶是圆柱与圆台组合,故D错误.
故选A.
6.【答案】B;
【解析】解:的补角
故选:
根据补角的定义求解即可.
此题主要考查的是补角的定义,掌握补角的定义是解答该题的关键.
7.【答案】D;
【解析】解:图中线段有:AD、AC、AB、DC、DB、CB,共6条.
故选D.
8.【答案】C;
【解析】
该题考查了点、线、面、体,重在体现面动成体:考查学生立体图形的空间想象能力及分析问题,解决问题的能力.解答该题的关键在于根据题意想象立体图形逐项分析即可得到答案.
解:是由半圆沿直径旋转得到的,此选项错误;
B.是由直角梯形沿直角腰旋转得到的,此选项错误;
C.是由直角三角形沿直角边旋转得到的,此选项正确;
D.是由长方形沿一边旋转得到的,此选项错误.
故选C.
9.【答案】D;
【解析】解:如图所示:
所以:,
故选:
根据题目已知画出图形,准确找到方位角即可.
此题主要考查了方位角,根据题意画出图形是解答该题的关键.
10.【答案】A;
【解析】
该题考查了线段的性质,直线的性质,以及角的定义,是基础题,熟记概念与各性质是解答该题的关键.
根据两点确定一条直线,角的定义,线段中点的定义对各选项分析判断后利用排除法求解.
解:、两点确定一条直线正确,故本选项正确;
B、应为有公共端点的两条射线组成的图形叫做角,故本选项错误;
C、应为两点之间线段最短,故本选项错误;
D、若,则点为的中点错误,因为、、三点不一定共线,故本选项错误.
故选A.
11.【答案】B;
【解析】略
12.【答案】C;
【解析】该题考查角的大小比较和度分秒之间的换算,在比较角的大小时有时可把度化为分来进行比较,首先同一单位,利用,把,,把度化为分,再进一步与比较得出答案即可.解:,,.故选C.
13.【答案】A;
【解析】解:是的中点,是的中点
,
,
.
故选A.
由是的中点,是的中点,则,,故AB可求.
考查了两点间的距离,首先根据线段的中点概念,写出需要的关系式.再根据题意,结合图形进行线段的和与差的计算.
14.【答案】B;
【解析】解:这是一个正方体的平面展开图,共有六个面,其中面“强”与面“提”相对,面“减”与面“质”相对,面“负”与面“课”相对.
故选:
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
此题主要考查了正方体相对两个面上的文字,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念是解决此类问题的关键.
15.【答案】C;
【解析】【试题解析】
这道题主要考查线段中点的定义和等量代换,只要细心进行线段的代换便不难得到正确答案.
根据和两种情况和对各选项分析后即不难选出答案.
解:是线段的中点,
,
A.,故本选项正确;
B.,故本选项正确;
C.,故本选项错误;
D.,故本选项正确.
故选C.
16.【答案】;
【解析】解:点半时,时针和分针中间相差个大格.
钟表个数字,每相邻两个数字之间的夹角为,
点半时分针与时针的夹角是.
画出草图,利用钟表表盘的特征解答.
用到的知识点为:钟表上个数字,每相邻两个数字之间的夹角为.
17.【答案】两 两点确定一条直线;
【解析】解:要把一根细木条固定在墙上,至少需要钉两个钉子,其中蕴含的数学道理是两点确定一条直线,
故答案为:两,两点确定一条直线.
根据直线的性质,可得答案.
此题主要考查了直线的性质,熟记直线的性质是解题关键.
18.【答案】84°;
【解析】解:设,则,
又平分,
,
,
,
即,
故答案为:.
此题可以设,,再进一步表示,根据角平分线的概念表示,最后根据已知角的度数列方程即可计算.
该题考查了角平分线的定义.此类题设恰当的未知数,根据已知条件进一步表示出相关的角,列方程计算较为简便.
19.【答案】2;1;0;
【解析】【略】。
20.【答案】10;
【解析】解:根据“相间、端是对面”可知:
的相对面是,则
的对立面是,则
的对立面是,则
所以
故答案是:
根据正方体展开图的特征,判断“对面”求出、、,再计算即可.
此题主要考查了相反数,正方体相对两个面上的文字,对于此类问题一般方法是用纸按图的样子折叠后可以解决,或是在对展开图理解的基础上直接想象.
21.【答案】解:∵BC=6cm,BD=7cm,
∴CD=BD-BC=1cm;
∵点D是AC的中点,
∴AD=CD=1cm.;
【解析】
由点是的中点,于是得到,根据线段的和差即可得到结论.
此题主要考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答该题的关键.
22.【答案】解:如图所示:
.;
【解析】【试题解析】
该题考查认识立体图形,掌握好从几个方向看立体图形所得图形的特点是解题关键.
由已知条件可知,从正面看的图形有列,每列小正方数形数目分别为,,;从左面看的图形有列,每列小正方数形数目分别为,,,据此可画出图形.
解:见答案;
在不改变从正面看的图形和上面看的图形的情况下,最多可添加个小正方体,
故答案为:.
23.【答案】解:由∠α、∠β都是∠θ的补角,得
∠α=∠β,即2n-1=68-n.
解得n=23;
∠α与∠β互余,理由如下:
∵∠α和∠β分别为(2n-1)°和(68-n)°,
∴∠α=(2n-1)°=45°,∠β=(68-n)°=45°,
∵∠α+∠β=90°,
∴∠α与∠β互为余角.;
【解析】
先根据补角的性质,可得,解这个方程,可得的值;根据余角的定义,可得答案.
此题主要考查了余角和补角.解答该题的关键是掌握余角和补角有关定义和性质.
24.【答案】平分 10或40;
【解析】解:直线平分
理由如下:
设的反向延长线为,
平分,,
,
又,
,
,
,
平分,
即直线平分,
故答案为:平分;
,
即旋转或时直线平分
由题意得,或
解得:或,
故答案为:或;
的差不变.
,,
、
与的差不变,这个差值是
设的反向延长线为,由角平分线的性质和对顶角的性质可求得;
由直线恰好平分锐角可知旋转或时直线平分,根据旋转速度可求得需要的时间;
由,,可知、,最后求得两角的差,从而可做出判断.
此题主要考查的是角的计算、角平分线的定义,用含的式子表示出和的长是解答该题的关键.
25.【答案】BC;6;AC;3;AB;1;
【解析】解:,,
,
,
为中点,
,
,
故答案为:,,,,,
求出长,根据线段中点求出,代入求出即可.
此题主要考查了线段中点和求两点间的距离的应用,关键是求出、长和得出
26.【答案】解:设这个角为x,则补角为(180°-x),余角为(90°-x),
由题意得,3(90°-x)=180°-x,
解得:x=45,
即这个角为45°.;
【解析】
根据互余的两角之和为,互补的两角之和为,表示出余角和补角,然后列方程求解即可.
该题考查了余角和补角的知识,属于基础题,关键是掌握互余的两角之和为,互补的两角之和为.
27.【答案】解:根据题意,画出的图形如图所示:;
是的中点,,
,
,
,
.;
【解析】该题考查的是两点间的距离,画线段以及中点的性质.
根据题意画出线段,利用中点的性质标出点即可;
由的长结合中点的性质得到的长,再根据线段和差的性质即可得到的长.
28.【答案】解:(1)根据图形可得线段BA与线段AB是同一条线段;
(2)由题意得:射线BC与射线DC的顶点不同,故不是同一条射线.;
【解析】(1)根据线段的定义及特点可得两者是同一条线段.
(2)根据射线的概念可判断出答案.
