活动单导学课程 苏教版高中数学选择性必修第一册第四章数列4.2.3 等差数列的前n项和(2)(有答案)
文档属性
| 名称 | 活动单导学课程 苏教版高中数学选择性必修第一册第四章数列4.2.3 等差数列的前n项和(2)(有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 193.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 15:58:17 | ||
图片预览


文档简介
4.2.3 等差数列的前n项和(2)
1. 能选取合适的等差数列的前n项和公式解决问题.
2. 探求等差数列前n项和的性质并能运用它们解决问题.
活动一 掌握等差数列前n项和公式的灵活运用
例1 在等差数列{an}中,Sn为前n项和.
(1) 已知a3=1,a5=11,求an和S8;
(2) 已知a2+a7+a12=24,求S13;
(3) 已知前4项和为25,最后4项和为63,前n项和为286,求项数n;
(4) 已知Sm=n,Sn=m(m≠n),求Sm+n.
在等差数列{an}的五个变量中,a1,n,d,an,Sn,可知三求二.若已知an,优先选用Sn=;若已知d,优先选用Sn=na1+d,同时在解题的过程中注意等差数列的性质:若m+n=p+q,则am+an=ap+aq的应用.
活动二 掌握等差数列前n项和的最值问题
例2 在等差数列{an}中,a1=50,d=-.
(1) 从第几项开始有an<0
(2) 求Sn的最大值.
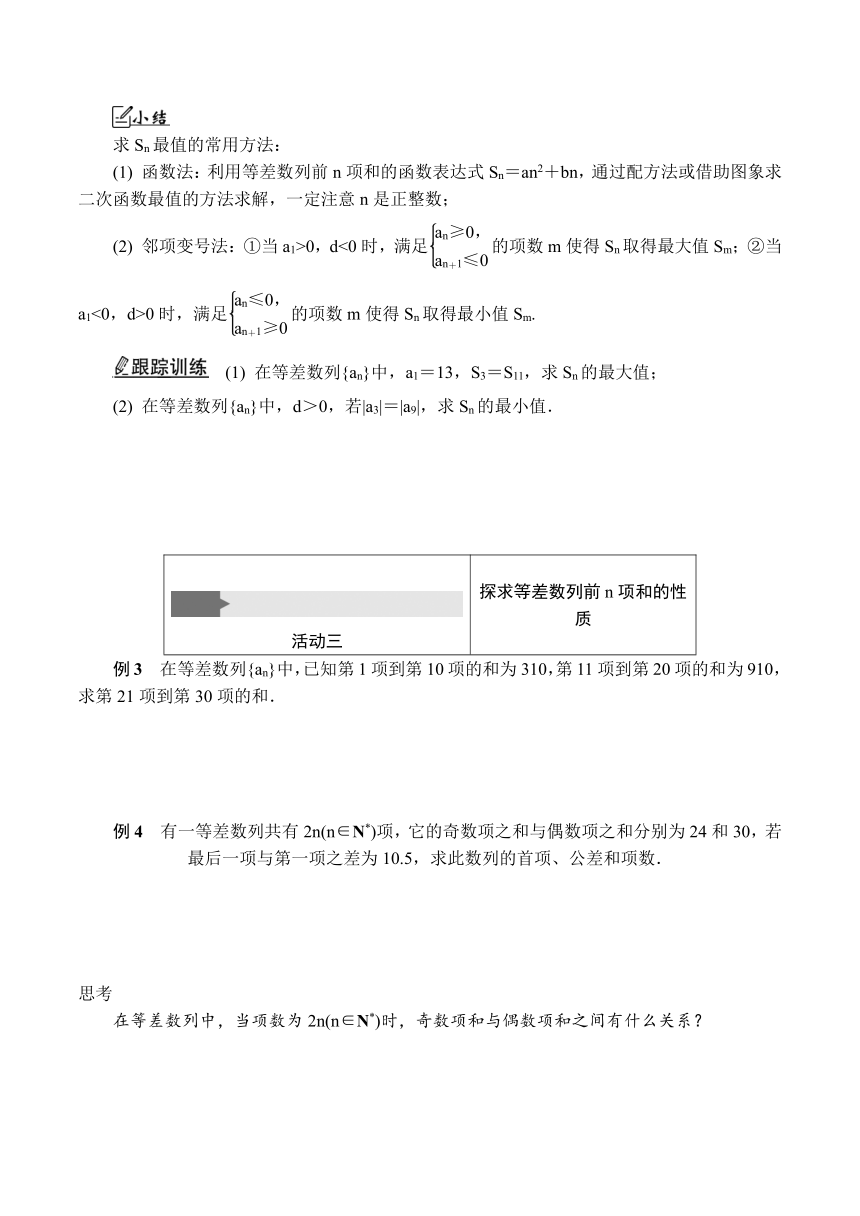
求Sn最值的常用方法:
(1) 函数法:利用等差数列前n项和的函数表达式Sn=an2+bn,通过配方法或借助图象求二次函数最值的方法求解,一定注意n是正整数;
(2) 邻项变号法:①当a1>0,d<0时,满足的项数m使得Sn取得最大值Sm;②当a1<0,d>0时,满足的项数m使得Sn取得最小值Sm.
(1) 在等差数列{an}中,a1=13,S3=S11,求Sn的最大值;
(2) 在等差数列{an}中,d>0,若|a3|=|a9|,求Sn的最小值.
活动三 探求等差数列前n项和的性质
例3 在等差数列{an}中,已知第1项到第10项的和为310,第11项到第20项的和为910,求第21项到第30项的和.
例4 有一等差数列共有2n(n∈N*)项,它的奇数项之和与偶数项之和分别为24和30,若最后一项与第一项之差为10.5,求此数列的首项、公差和项数.
思考
在等差数列中,当项数为2n(n∈N*)时,奇数项和与偶数项和之间有什么关系?
探究:若一个等差数列共有2n+1(n∈N*)项,则其奇数项和与偶数项和有什么关系?
例5 有两个等差数列{an},{bn},其前n项和分别为Tn,Sn,且=,求.
在例5的条件下,求:
(1) ;(2) ;(3) .
若有两个等差数列{an},{bn},其前n项和分别为Tn,Sn,则=________.
1. 设Sn是等差数列{an}的前n项和,若a1+a3+a5=3,则S5等于( )
A. 5 B. 7 C. 9 D. 11
2. 已知两个等差数列{an}和{bn}的前n项和分别是An和Bn,且=,则等于( )
A. 2 B. C. D.
3. (多选)设{an}是等差数列,Sn是其前n项和,且S5S8,则下列结论中正确的是( )
A. d<0 B. a7=0
C. S9>S5 D. S6与S7均为Sn的最大值
4. 一个等差数列的前12项和为354,前12项中偶数项的和与奇数项的和之比为,则公差d=________.
5. 设等差数列{an}的前n项和为Sn,已知a3=12,S12>0,S13<0.
(1) 求公差d的取值范围;
(2) 指出S1,S2,S3,…,S12中哪一个值最大,并说明理由.
参考答案与解析
【活动方案】
例1 (1) 因为a3=1,a5=11,
所以d===5,
所以a1=a3-2d=1-10=-9,
所以an=-9+5(n-1)=5n-14,
S8=8×(-9)+×5=68.
(2) 因为{an}是等差数列,
所以a1+a13=a2+a12=2a7,
所以a2+a7+a12=3a7=24,即a7=8,
所以a1+a13=16,
所以S13===104.
(3) 由题意知a1+a2+a3+a4=25,
an-3+an-2+an-1+an=63.
因为{an}是等差数列,
所以a1+an=a2+an-1=a3+an-2=a4+an-3,
所以4(a1+an)=25+63=88,
即a1+an=22.
因为Sn==286,
所以n=26.
(4) 设Sn=An2+Bn,由题意,得
①-②,得A(m2-n2)+B(m-n)=n-m.
因为m≠n,所以(m+n)A+B=-1,
所以Sm+n=A(m+n)2+B(m+n)=-(m+n).
例2 (1) 因为a1=50,d=-,
所以an=50+(n-1)×.
令an<0,得50+(n-1)×<0,
解得n>=84.
因为n∈N*,所以从第85项开始有an<0.
(2) 由(1)知从第85项开始有an<0,
所以Sn的最大值为S84.
因为a1=50,d=-,
所以S84=84×50-×=2 108.4.
跟踪训练 (1) 因为a1=13,S3=S11,
所以3a1+d=11a1+d,
所以d=-2,
所以Sn=13n+×(-2)
=-n2+14n=-(n-7)2+49,
所以当n=7时,Sn取得最大值49.
(2) 因为d>0,所以-a3=a9,所以a1=-5d.
因为Sn=na1+d
=,
所以当n=5或n=6时,Sn取得最小值,
最小值为S5=S6=-15d.
例3 由题意知a1+a2+…+a10=310,①
a11+a12+…+a20=910,②
设S=a21+a22+…+a30,③
因为{an}是等差数列,
所以由②-①,得10d+10d+…+10d=600,
由③-②,得10d+10d+…+10d=S-910,
所以S-910=600,所以S=1 510,
即第21项到第30项的和为1 510.
例4 设此数列为{an},其公差为d,前n项和为Sn,
由题意知
解得
因为a1+a3+a5+a7=4a1+12d=24,
所以a1=,
所以此数列的首项为,公差为,项数为8.
思考:若项数为2n(n∈N*),则S偶-S奇=nd,=.
探究:S奇-S偶=an+1(an+1为中间项),=.
例5 =====.
跟踪训练 (1) ====.
(2) ====.
(3) 设Tn=(7n+2)k,Sn=(n+3)k,k≠0,
所以a5=T5-T4=37k-30k=7k,
b6=S6-S5=9k-8k=k,所以==7.
小结
【检测反馈】
1. A 解析:因为a1+a3+a5=3a3=3,所以a3=1,所以S5=(a1+a5)=×2a3=5a3=5.
2. B 解析:由等差数列的性质可知=====.
3. ABD 解析:由S50,即a6>0.由S6=S7,得S7-S6=a7=0.由S7>S8,得S8-S7=a8<0,所以数列{an}是递减数列,故d<0,故A,B正确;因为S9-S5=a6+a7+a8+a9=2(a7+a8)<0,所以S90,a7=0,a8<0,所以S6与S7均为Sn的最大值,故D正确.故选ABD.
4. 5 解析:由题意,得S偶=192,S奇=162,所以S偶-S奇=6d=30,即d=5.
5. (1) 由题意,得
因为a3=12,所以a1=12-2d,
代入,得解得-即公差d的取值范围为.
(2) 因为S12>0,S13<0,d<0,
所以即
所以所以S6的值最大.
1. 能选取合适的等差数列的前n项和公式解决问题.
2. 探求等差数列前n项和的性质并能运用它们解决问题.
活动一 掌握等差数列前n项和公式的灵活运用
例1 在等差数列{an}中,Sn为前n项和.
(1) 已知a3=1,a5=11,求an和S8;
(2) 已知a2+a7+a12=24,求S13;
(3) 已知前4项和为25,最后4项和为63,前n项和为286,求项数n;
(4) 已知Sm=n,Sn=m(m≠n),求Sm+n.
在等差数列{an}的五个变量中,a1,n,d,an,Sn,可知三求二.若已知an,优先选用Sn=;若已知d,优先选用Sn=na1+d,同时在解题的过程中注意等差数列的性质:若m+n=p+q,则am+an=ap+aq的应用.
活动二 掌握等差数列前n项和的最值问题
例2 在等差数列{an}中,a1=50,d=-.
(1) 从第几项开始有an<0
(2) 求Sn的最大值.
求Sn最值的常用方法:
(1) 函数法:利用等差数列前n项和的函数表达式Sn=an2+bn,通过配方法或借助图象求二次函数最值的方法求解,一定注意n是正整数;
(2) 邻项变号法:①当a1>0,d<0时,满足的项数m使得Sn取得最大值Sm;②当a1<0,d>0时,满足的项数m使得Sn取得最小值Sm.
(1) 在等差数列{an}中,a1=13,S3=S11,求Sn的最大值;
(2) 在等差数列{an}中,d>0,若|a3|=|a9|,求Sn的最小值.
活动三 探求等差数列前n项和的性质
例3 在等差数列{an}中,已知第1项到第10项的和为310,第11项到第20项的和为910,求第21项到第30项的和.
例4 有一等差数列共有2n(n∈N*)项,它的奇数项之和与偶数项之和分别为24和30,若最后一项与第一项之差为10.5,求此数列的首项、公差和项数.
思考
在等差数列中,当项数为2n(n∈N*)时,奇数项和与偶数项和之间有什么关系?
探究:若一个等差数列共有2n+1(n∈N*)项,则其奇数项和与偶数项和有什么关系?
例5 有两个等差数列{an},{bn},其前n项和分别为Tn,Sn,且=,求.
在例5的条件下,求:
(1) ;(2) ;(3) .
若有两个等差数列{an},{bn},其前n项和分别为Tn,Sn,则=________.
1. 设Sn是等差数列{an}的前n项和,若a1+a3+a5=3,则S5等于( )
A. 5 B. 7 C. 9 D. 11
2. 已知两个等差数列{an}和{bn}的前n项和分别是An和Bn,且=,则等于( )
A. 2 B. C. D.
3. (多选)设{an}是等差数列,Sn是其前n项和,且S5
A. d<0 B. a7=0
C. S9>S5 D. S6与S7均为Sn的最大值
4. 一个等差数列的前12项和为354,前12项中偶数项的和与奇数项的和之比为,则公差d=________.
5. 设等差数列{an}的前n项和为Sn,已知a3=12,S12>0,S13<0.
(1) 求公差d的取值范围;
(2) 指出S1,S2,S3,…,S12中哪一个值最大,并说明理由.
参考答案与解析
【活动方案】
例1 (1) 因为a3=1,a5=11,
所以d===5,
所以a1=a3-2d=1-10=-9,
所以an=-9+5(n-1)=5n-14,
S8=8×(-9)+×5=68.
(2) 因为{an}是等差数列,
所以a1+a13=a2+a12=2a7,
所以a2+a7+a12=3a7=24,即a7=8,
所以a1+a13=16,
所以S13===104.
(3) 由题意知a1+a2+a3+a4=25,
an-3+an-2+an-1+an=63.
因为{an}是等差数列,
所以a1+an=a2+an-1=a3+an-2=a4+an-3,
所以4(a1+an)=25+63=88,
即a1+an=22.
因为Sn==286,
所以n=26.
(4) 设Sn=An2+Bn,由题意,得
①-②,得A(m2-n2)+B(m-n)=n-m.
因为m≠n,所以(m+n)A+B=-1,
所以Sm+n=A(m+n)2+B(m+n)=-(m+n).
例2 (1) 因为a1=50,d=-,
所以an=50+(n-1)×.
令an<0,得50+(n-1)×<0,
解得n>=84.
因为n∈N*,所以从第85项开始有an<0.
(2) 由(1)知从第85项开始有an<0,
所以Sn的最大值为S84.
因为a1=50,d=-,
所以S84=84×50-×=2 108.4.
跟踪训练 (1) 因为a1=13,S3=S11,
所以3a1+d=11a1+d,
所以d=-2,
所以Sn=13n+×(-2)
=-n2+14n=-(n-7)2+49,
所以当n=7时,Sn取得最大值49.
(2) 因为d>0,所以-a3=a9,所以a1=-5d.
因为Sn=na1+d
=,
所以当n=5或n=6时,Sn取得最小值,
最小值为S5=S6=-15d.
例3 由题意知a1+a2+…+a10=310,①
a11+a12+…+a20=910,②
设S=a21+a22+…+a30,③
因为{an}是等差数列,
所以由②-①,得10d+10d+…+10d=600,
由③-②,得10d+10d+…+10d=S-910,
所以S-910=600,所以S=1 510,
即第21项到第30项的和为1 510.
例4 设此数列为{an},其公差为d,前n项和为Sn,
由题意知
解得
因为a1+a3+a5+a7=4a1+12d=24,
所以a1=,
所以此数列的首项为,公差为,项数为8.
思考:若项数为2n(n∈N*),则S偶-S奇=nd,=.
探究:S奇-S偶=an+1(an+1为中间项),=.
例5 =====.
跟踪训练 (1) ====.
(2) ====.
(3) 设Tn=(7n+2)k,Sn=(n+3)k,k≠0,
所以a5=T5-T4=37k-30k=7k,
b6=S6-S5=9k-8k=k,所以==7.
小结
【检测反馈】
1. A 解析:因为a1+a3+a5=3a3=3,所以a3=1,所以S5=(a1+a5)=×2a3=5a3=5.
2. B 解析:由等差数列的性质可知=====.
3. ABD 解析:由S5
4. 5 解析:由题意,得S偶=192,S奇=162,所以S偶-S奇=6d=30,即d=5.
5. (1) 由题意,得
因为a3=12,所以a1=12-2d,
代入,得解得-
(2) 因为S12>0,S13<0,d<0,
所以即
所以所以S6的值最大.
