2022-2023学年度北师大版九年级数学下册3.2 圆的对称性 课件 (共17张PPT)
文档属性
| 名称 | 2022-2023学年度北师大版九年级数学下册3.2 圆的对称性 课件 (共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 08:33:07 | ||
图片预览






文档简介
(共17张PPT)
第三章
圆
3.2 圆的对称性
授课人:XXXX
九年级数学北师版·下册
教学目标
1. 经历探索圆的对称性、旋转不变性及相关性质的过程.
2. 理解圆的旋转不变性和中心对称性,掌握圆心角、弧、弦之间相等关系定理.
新课导入
情境引入
1. 圆是轴对称图形,其对称轴是任意一条过 的直线.圆的对称轴有 .
2. 圆具有旋转不变性.一个圆绕着它的圆心旋转任意角度,都能与原来的图形 .由此可得,圆是中心对称图形,对称中心是 .
圆心
无数条
重合
圆心
新课导入
(一)圆的对称性
(1)圆是轴对称图形,其对称轴是任意一条过圆心的直线 .
(2)圆是中心对称图形,对称中心为圆心.
新课导入
圆绕圆心旋转任意角度α,都能够与原来的图形重合.
____________________.
若旋转角度不是180°,而是旋转任意角度,则旋
转过后的图形能与原图形重合吗?
B
O
A
α
圆具有旋转不变性
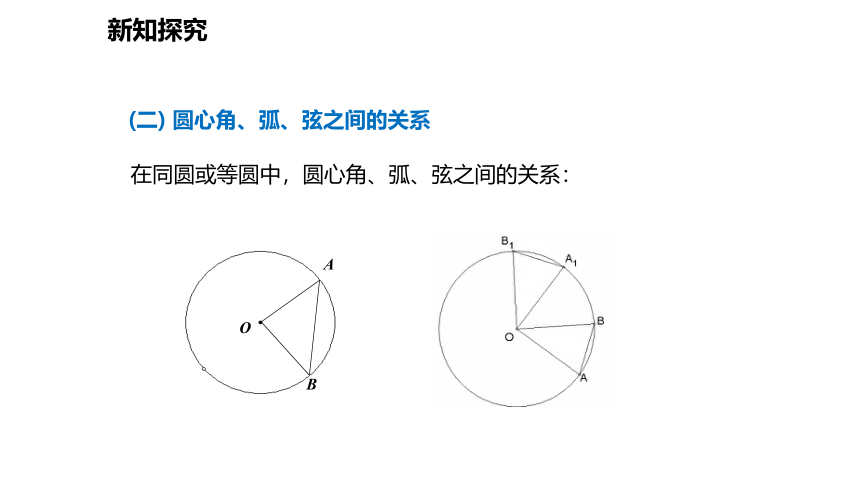
新知探究
在同圆或等圆中,圆心角、弧、弦之间的关系:
O
B
A
(二) 圆心角、弧、弦之间的关系
新知探究
________________,相等的圆心角所对的弧相等,所对的弦相等.
________________,如果两个圆心角、两条弧、两
条弦中有一组量相等,那么它们所对应的其余各
组量都分别相等.
在同圆或等圆中
在同圆或等圆中
【定理】
【推论】
新知探究
例1:如图,点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点 A,B和C,D,求证:AB=CD.
证明:作OM⊥AB,
ON⊥CD,M,N为垂足.
M
O
N
E
B
A
P
C
D
F
新知探究
1.已知:如图,AB,CD是⊙O的两条弦,OE,OF为AB,CD的弦心距,根据本节定理及推论填空:
(1)如果AB=CD,那么
, , _________.
(2)如果OE=OF,那么
, , __________.
∠AOB=∠COD OE=OF AB=CD
⌒
⌒
∠AOB=∠COD AB=CD AB=CD
⌒
⌒
【跟踪训练】
O
A
B
C
D
F
E
新知探究
OE=OF AB=CD
⌒
⌒
AB=CD
∠AOB=∠COD OE=OF
AB=CD
(3)如果AB=CD , 那么
____________ , __________ , _________ .
(4)如果∠AOB=∠COD,那么
_________ , ________ , _________.
⌒
⌒
新知探究
例2 : A,B分别为CD和EF的中点,AB分别交CD,EF于点M,N,且AM=BN.求证:CD=EF.
F
G
⌒
⌒
证明:连接OA,OB,设分别与CD,EF交于点F,G.
∵A为 中点,B为 中点,
∴OA⊥CD,OB⊥EF.
新知探究
故∠AFC=∠BGE=90°
又由OA=OB,
∴∠OAB=∠OBA,
且 AM=BN,
∴△AFM ≌ △BGN,
∴AF=BG,
∴OF=OG,
∴DC=EF.
新知探究
证明:分别作O1C1⊥A1B1,
O2C2 ⊥ A2B2,垂足分别
为C1,C2,
∵A1B2∥O1O2,
∴O1C1= O2C2.
如图:⊙O1和⊙O2是两个等圆,直线O1O2平行于A1B2. 分别交⊙O1于点A1,B1,交⊙O2于点A2,B2.
求证:∠A1O1B1= ∠A2O2B2 .
【跟踪训练】
∴∠A1O1B1= ∠A2O2B2 .
A1
B1
C1
A2
C2
B2
O1
O2
课堂小结
圆的对称性
圆的中心对称性(圆是中心对称图形)
圆心角、弧、弦之间的关系
证明圆弧相等:(1)定义
(2)圆心角、弧、弦之间的关系
证明线段相等:(1)利用原来的证角相等、三角形全等等方法
(2)圆心角、弧、弦之间的关系
圆的轴对称性(圆是轴对称图形)
对称轴是过圆心的直线
课堂小测
证明:
又∠ACB=60°,
∴△ABC是等边三角形, AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
·
A
B
C
O
△ABC是等腰三角形.
1、如图,在⊙O中,AB=AC , ∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
⌒
⌒
∵AB=AC , ∴ AB=AC,
⌒
⌒
课堂小测
·
A
O
B
C
D
E
解:
∴ ∠BOC=∠COD=∠DOE=35°.
2 . 如图,AB是⊙O 的直径,BC=CD=DE,∠COD=35°
求∠AOE 的度数.
⌒
⌒
⌒
∵ BC=CD=DE
⌒
⌒
⌒
∴ ∠AOE=180°-3×35 °
=75°.
第三章
圆
3.2 圆的对称性
授课人:XXXX
九年级数学北师版·下册
教学目标
1. 经历探索圆的对称性、旋转不变性及相关性质的过程.
2. 理解圆的旋转不变性和中心对称性,掌握圆心角、弧、弦之间相等关系定理.
新课导入
情境引入
1. 圆是轴对称图形,其对称轴是任意一条过 的直线.圆的对称轴有 .
2. 圆具有旋转不变性.一个圆绕着它的圆心旋转任意角度,都能与原来的图形 .由此可得,圆是中心对称图形,对称中心是 .
圆心
无数条
重合
圆心
新课导入
(一)圆的对称性
(1)圆是轴对称图形,其对称轴是任意一条过圆心的直线 .
(2)圆是中心对称图形,对称中心为圆心.
新课导入
圆绕圆心旋转任意角度α,都能够与原来的图形重合.
____________________.
若旋转角度不是180°,而是旋转任意角度,则旋
转过后的图形能与原图形重合吗?
B
O
A
α
圆具有旋转不变性
新知探究
在同圆或等圆中,圆心角、弧、弦之间的关系:
O
B
A
(二) 圆心角、弧、弦之间的关系
新知探究
________________,相等的圆心角所对的弧相等,所对的弦相等.
________________,如果两个圆心角、两条弧、两
条弦中有一组量相等,那么它们所对应的其余各
组量都分别相等.
在同圆或等圆中
在同圆或等圆中
【定理】
【推论】
新知探究
例1:如图,点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点 A,B和C,D,求证:AB=CD.
证明:作OM⊥AB,
ON⊥CD,M,N为垂足.
M
O
N
E
B
A
P
C
D
F
新知探究
1.已知:如图,AB,CD是⊙O的两条弦,OE,OF为AB,CD的弦心距,根据本节定理及推论填空:
(1)如果AB=CD,那么
, , _________.
(2)如果OE=OF,那么
, , __________.
∠AOB=∠COD OE=OF AB=CD
⌒
⌒
∠AOB=∠COD AB=CD AB=CD
⌒
⌒
【跟踪训练】
O
A
B
C
D
F
E
新知探究
OE=OF AB=CD
⌒
⌒
AB=CD
∠AOB=∠COD OE=OF
AB=CD
(3)如果AB=CD , 那么
____________ , __________ , _________ .
(4)如果∠AOB=∠COD,那么
_________ , ________ , _________.
⌒
⌒
新知探究
例2 : A,B分别为CD和EF的中点,AB分别交CD,EF于点M,N,且AM=BN.求证:CD=EF.
F
G
⌒
⌒
证明:连接OA,OB,设分别与CD,EF交于点F,G.
∵A为 中点,B为 中点,
∴OA⊥CD,OB⊥EF.
新知探究
故∠AFC=∠BGE=90°
又由OA=OB,
∴∠OAB=∠OBA,
且 AM=BN,
∴△AFM ≌ △BGN,
∴AF=BG,
∴OF=OG,
∴DC=EF.
新知探究
证明:分别作O1C1⊥A1B1,
O2C2 ⊥ A2B2,垂足分别
为C1,C2,
∵A1B2∥O1O2,
∴O1C1= O2C2.
如图:⊙O1和⊙O2是两个等圆,直线O1O2平行于A1B2. 分别交⊙O1于点A1,B1,交⊙O2于点A2,B2.
求证:∠A1O1B1= ∠A2O2B2 .
【跟踪训练】
∴∠A1O1B1= ∠A2O2B2 .
A1
B1
C1
A2
C2
B2
O1
O2
课堂小结
圆的对称性
圆的中心对称性(圆是中心对称图形)
圆心角、弧、弦之间的关系
证明圆弧相等:(1)定义
(2)圆心角、弧、弦之间的关系
证明线段相等:(1)利用原来的证角相等、三角形全等等方法
(2)圆心角、弧、弦之间的关系
圆的轴对称性(圆是轴对称图形)
对称轴是过圆心的直线
课堂小测
证明:
又∠ACB=60°,
∴△ABC是等边三角形, AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
·
A
B
C
O
△ABC是等腰三角形.
1、如图,在⊙O中,AB=AC , ∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
⌒
⌒
∵AB=AC , ∴ AB=AC,
⌒
⌒
课堂小测
·
A
O
B
C
D
E
解:
∴ ∠BOC=∠COD=∠DOE=35°.
2 . 如图,AB是⊙O 的直径,BC=CD=DE,∠COD=35°
求∠AOE 的度数.
⌒
⌒
⌒
∵ BC=CD=DE
⌒
⌒
⌒
∴ ∠AOE=180°-3×35 °
=75°.
