全等三角形[上学期]
图片预览



文档简介
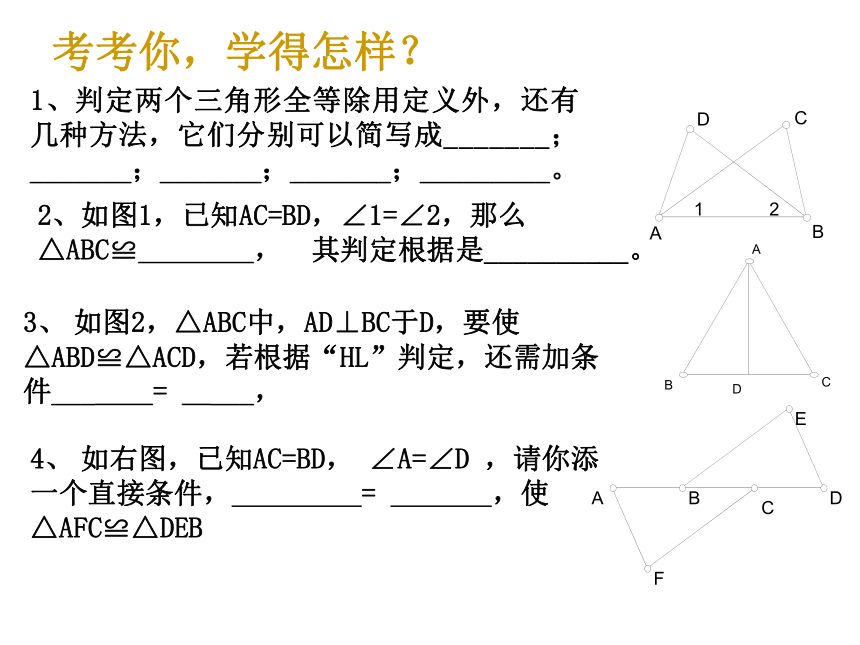
课件14张PPT。三角形全等(复习)考考你,学得怎样?1、判定两个三角形全等除用定义外,还有几种方法,它们分别可以简写成_______;_______;_______;_______;_________。2、如图1,已知AC=BD,∠1=∠2,那么△ABC≌ , 其判定根据是__________。3、 如图2,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,还需加条件___ = ___,4、 如右图,已知AC=BD, ∠A=∠D ,请你添一个直接条件, = ,使△AFC≌△DEB5、如图,已知AB=AC,BE=CE,延长AE交BC于D,则图中全等三角形共有( )
(A)1对 (B)2对 (C)3对 (D)4对6、下列条件中,不能判定两个直角三角形全等的是( )
(A)一锐角和斜边对应相等 (B)两条直角边对应相等
(C)斜边和一直角边对应相等 (D)两个锐角对应相等7、下列四组中一定是全等三角形的为 ( )
A.三内角分别对应相等的两三角形 B、斜边相等的两直角三角形
(C、两边和其中一条边的对角对应相等的两个三角形
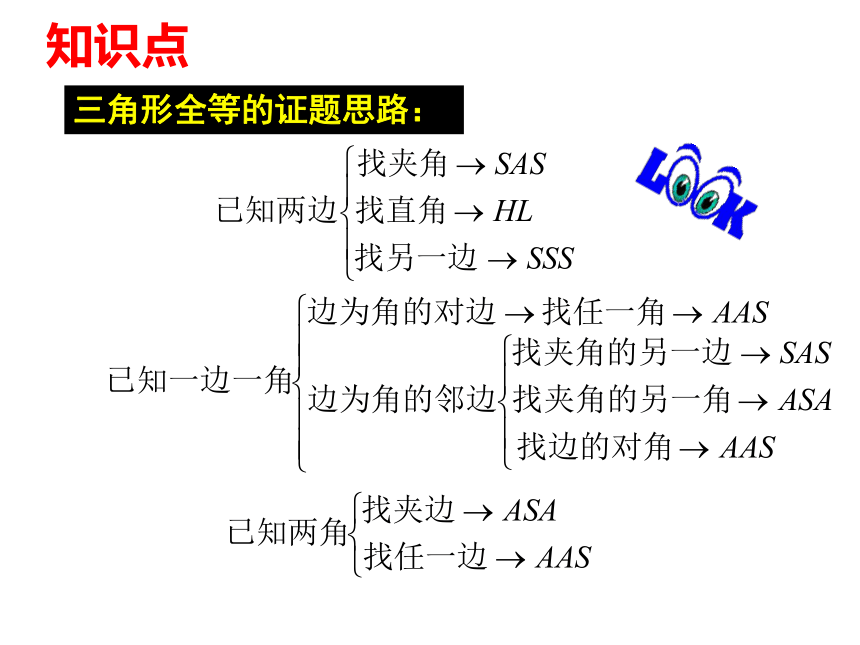
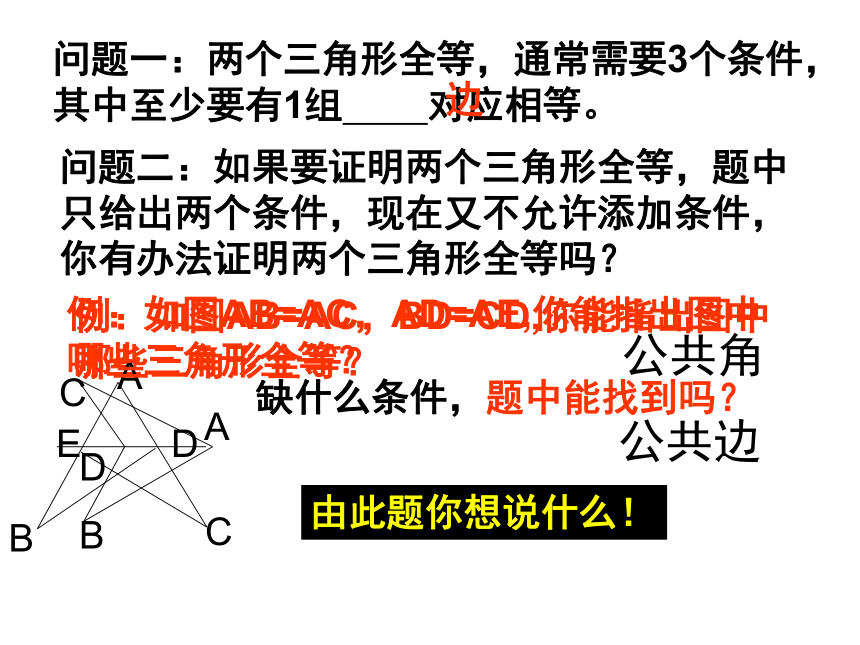
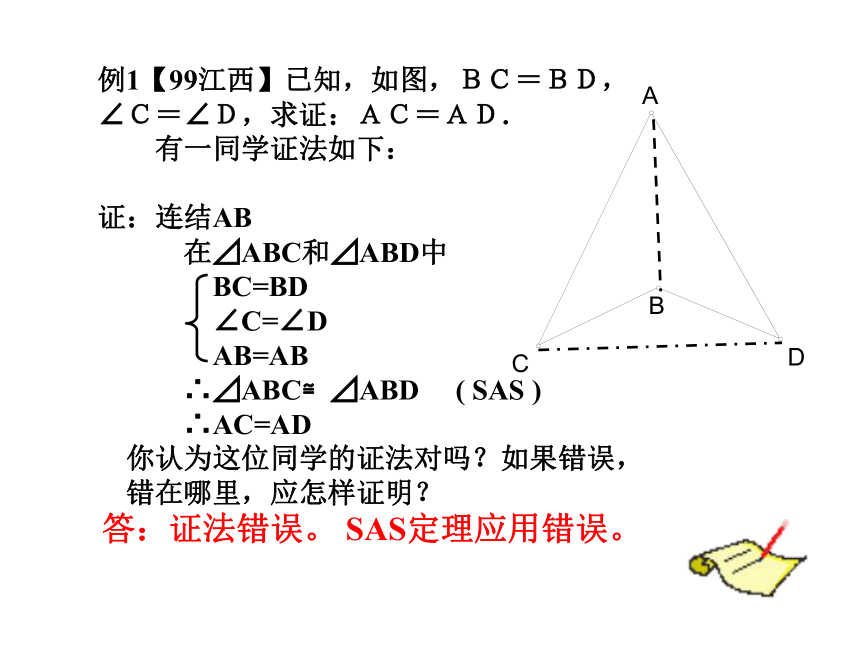
D、三边对应相等的两个三角形知识点三角形全等的证题思路:问题一:两个三角形全等,通常需要3个条件,其中至少要有1组 对应相等。边问题二:如果要证明两个三角形全等,题中只给出两个条件,现在又不允许添加条件,你有办法证明两个三角形全等吗?缺什么条件,题中能找到吗?公共角由此题你想说什么!例:如图AB=AC,BD=CD,你能指出图中哪些三角形全等?公共边基本图形演变答:证法错误。 SAS定理应用错误。试一试,你准行 2、已知:AB=AC,EB=EC,AE的延长线交BC于D,
试说明:BD=CD解:在△ABE和△ACE中
AB=AC,EB=EC,AE=AE
∴ △ABE≌△ACE (SSS)
∴∠BAE=∠CAE
在△ABD和△ACD中
∵AB=AC ∠BAE= ∠CAE AD=AD
∴ △ABD≌ △ACD (SAS )
∴ BD = CD如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,CD=1.7cm。求:BE的长。说一说: 在一次战役中,我军阵地与敌人碉堡隔河相望,需要知道碉堡与我军阵地的距离。在不能过河测量又没有任何测量工具的情况下,一个战士利用他头上的帽子就测出了我军阵地与敌人碉堡的距离。你知道他用的是什么方法?其中的原理是什么?试一试
已知:A、B两点之间被一个池塘隔开,无法直接测量A、B间的距离,请给出一个适合可行的方案,画出设计图,说明依据。ECDCDCD议一议如图,在△ABC中, ∠ACB=90°,AO是角平分线,点D在AC的延长线上,DE过点O且DE⊥AB,垂足为E.
(1) 请你找出图中一对相等的线段,并说明它们相等的理由; 解:∵∠ACB=90°
∴BC⊥AC
∵AO平分∠BAC
又DE⊥AB BC⊥AC
∴OE=OC(角平分线上的点到角两边的距离相等 (2)图中共有多少对相等线段,一一把它们找出来,
并说明理由
(A)1对 (B)2对 (C)3对 (D)4对6、下列条件中,不能判定两个直角三角形全等的是( )
(A)一锐角和斜边对应相等 (B)两条直角边对应相等
(C)斜边和一直角边对应相等 (D)两个锐角对应相等7、下列四组中一定是全等三角形的为 ( )
A.三内角分别对应相等的两三角形 B、斜边相等的两直角三角形
(C、两边和其中一条边的对角对应相等的两个三角形
D、三边对应相等的两个三角形知识点三角形全等的证题思路:问题一:两个三角形全等,通常需要3个条件,其中至少要有1组 对应相等。边问题二:如果要证明两个三角形全等,题中只给出两个条件,现在又不允许添加条件,你有办法证明两个三角形全等吗?缺什么条件,题中能找到吗?公共角由此题你想说什么!例:如图AB=AC,BD=CD,你能指出图中哪些三角形全等?公共边基本图形演变答:证法错误。 SAS定理应用错误。试一试,你准行 2、已知:AB=AC,EB=EC,AE的延长线交BC于D,
试说明:BD=CD解:在△ABE和△ACE中
AB=AC,EB=EC,AE=AE
∴ △ABE≌△ACE (SSS)
∴∠BAE=∠CAE
在△ABD和△ACD中
∵AB=AC ∠BAE= ∠CAE AD=AD
∴ △ABD≌ △ACD (SAS )
∴ BD = CD如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,CD=1.7cm。求:BE的长。说一说: 在一次战役中,我军阵地与敌人碉堡隔河相望,需要知道碉堡与我军阵地的距离。在不能过河测量又没有任何测量工具的情况下,一个战士利用他头上的帽子就测出了我军阵地与敌人碉堡的距离。你知道他用的是什么方法?其中的原理是什么?试一试
已知:A、B两点之间被一个池塘隔开,无法直接测量A、B间的距离,请给出一个适合可行的方案,画出设计图,说明依据。ECDCDCD议一议如图,在△ABC中, ∠ACB=90°,AO是角平分线,点D在AC的延长线上,DE过点O且DE⊥AB,垂足为E.
(1) 请你找出图中一对相等的线段,并说明它们相等的理由; 解:∵∠ACB=90°
∴BC⊥AC
∵AO平分∠BAC
又DE⊥AB BC⊥AC
∴OE=OC(角平分线上的点到角两边的距离相等 (2)图中共有多少对相等线段,一一把它们找出来,
并说明理由
