12.2.4三角形全等的判定-HL 课件(共18张PPT)
文档属性
| 名称 | 12.2.4三角形全等的判定-HL 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 21:47:03 | ||
图片预览





文档简介
(共18张PPT)
12.2.4三角形全等的判定-HL
人教版 八年级 上册
教学目标
教学目标:1.探索并理解直角三角形全等的判定方法“HL”.
2.会用直角三角形全等的判定方法“HL”判定两个直角三角形全等.
教学重点: 理解、掌握直角三角形全等的条件:HL.
教学难点:熟练选择判定方法,判定两个直角三角形全等.
新知导入
情境引入
如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.
(1)你能帮他想个办法吗?
方法一:测量斜边和一个对应的锐角. (AAS)
方法二:测量没遮住的一条直角边和一个对应的锐角. ASA或(AAS)
新知讲解
合作学习
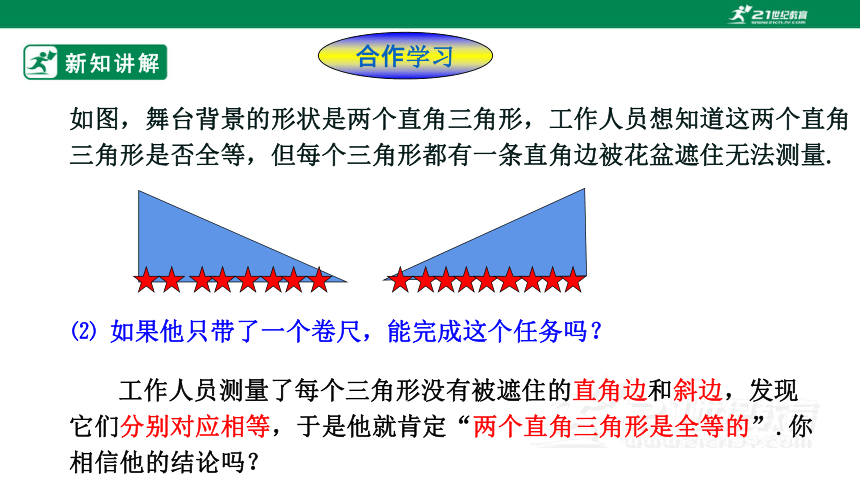
如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.
⑵ 如果他只带了一个卷尺,能完成这个任务吗?
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗?
问题:如何探究直角三角形专属的全等的判定方法呢?
类比最开始判定三角形全等的时候,我们是从 条件开始探究的,所以直角三角形全等,我们可以尝试从这个角度进行探究。
边
A
B
C
任意画一个Rt△ABC,使∠C=90°,再画一个Rt△A′B′C′使∠C′ =90°.B′C′=BC,A′B′=AB,然后把画好的Rt△A′ B′ C′剪下来放到Rt△ABC上,你发现了什么?
探究
A
B
C
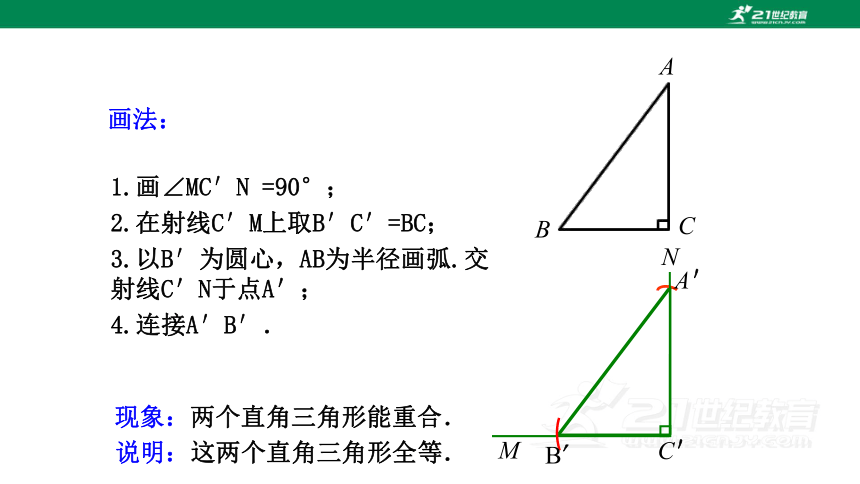
1.画∠MC′N =90°;
2.在射线C′M上取B′C′=BC;
3.以B′为圆心,AB为半径画弧.交射线C'N于点A';
4.连接A′B′.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
A'
N
M
C'
B′
画法:
提炼概念
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
“SSA”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.
AB=A′B′,
BC=B′C′,
巩固练习
判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等; ( )
(2)一个锐角和这个角的邻边对应相等; ( )
(3)一个锐角和斜边对应相等; ( )
(4)两直角边对应相等; ( )
(5)一条直角边和斜边对应相等 ( )
HL
AAS或ASA
SAS
AAS
AAS
判一判
典例精讲
例1 如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD.
证明: ∵ AC⊥BC, BD⊥AD, ∴∠C与∠D都是直角.
AB=BA,
AC=BD .
在 Rt△ABC 和Rt△BAD 中,
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD.
A
B
D
C
归纳概念
新知归纳
已知条件 可选择的判定方法 需寻找的条件
一锐角对应相等
斜边对应相等
一直角边对应相等
直角三角形全等方法大归纳
ASA或AAS
可证直角与已知锐角的夹边对应相等或者与锐角(或直角)的对边对应相等
HL或AAS
可证一直角边对应相等或证一锐角对应相等
HL或ASA或AAS
可证斜边对应相等或证已知边相邻的锐角对应相等或证已知边所对的锐角对应相等
A'
B'
C'
A
B
C
课堂练习
1.下列说法不正确的是( )
A.两条直角边对应相等的两个直角三角形全等
B.一锐角和斜边对应相等的两个直角三角形全等
C.斜边和一直角边对应相等的两个直角三角形全等
D.有两边相等的两个直角三角形全等
D
2. 如图,在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE.求证:△EBC≌△DCB.
A
B
C
E
D
证明: ∵ BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中,
CE=BD,
BC=CB .
∴ Rt△EBC≌Rt△DCB (HL).
典例讲解
3.如图,有两个长度相同的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系?为什么?
解:在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF .
∴ Rt△ABC≌Rt△DEF (HL).
∵ ∠DEF+∠F=90°,
∴∠B+∠F=90°.
4.已知:如图,在△ABC和△DEF中,AP、DQ分别是高,并且
AB=DE,AP=DQ,∠BAC=∠EDF,求证:△ABC≌△DEF
A
C
P
D
E
F
Q
B
证明:∵AP、DQ是△ABC和△DEF的高
∴∠APB=∠DQE=90°
在Rt△ABP和Rt△DEQ中
AB=DE
AP=DQ
∴Rt△ABP≌Rt△DEQ (HL)
∴ ∠B=∠E
在△ABC和△DEF中
∠BAC=∠EDF
AB=DE
∠B=∠E
∴△ABC≌△DEF (ASA)
课堂总结
“斜边、直角边”
内容
斜边和一条直角边对应相等的两个直角三角形全等.
前提条件
在直角三角形中
使用方法
只须找除直角外的两个条件即可(两个条件中至少有一个条件是一对对应边相等)
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
12.2.4三角形全等的判定-HL
人教版 八年级 上册
教学目标
教学目标:1.探索并理解直角三角形全等的判定方法“HL”.
2.会用直角三角形全等的判定方法“HL”判定两个直角三角形全等.
教学重点: 理解、掌握直角三角形全等的条件:HL.
教学难点:熟练选择判定方法,判定两个直角三角形全等.
新知导入
情境引入
如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.
(1)你能帮他想个办法吗?
方法一:测量斜边和一个对应的锐角. (AAS)
方法二:测量没遮住的一条直角边和一个对应的锐角. ASA或(AAS)
新知讲解
合作学习
如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.
⑵ 如果他只带了一个卷尺,能完成这个任务吗?
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗?
问题:如何探究直角三角形专属的全等的判定方法呢?
类比最开始判定三角形全等的时候,我们是从 条件开始探究的,所以直角三角形全等,我们可以尝试从这个角度进行探究。
边
A
B
C
任意画一个Rt△ABC,使∠C=90°,再画一个Rt△A′B′C′使∠C′ =90°.B′C′=BC,A′B′=AB,然后把画好的Rt△A′ B′ C′剪下来放到Rt△ABC上,你发现了什么?
探究
A
B
C
1.画∠MC′N =90°;
2.在射线C′M上取B′C′=BC;
3.以B′为圆心,AB为半径画弧.交射线C'N于点A';
4.连接A′B′.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
A'
N
M
C'
B′
画法:
提炼概念
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
“SSA”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.
AB=A′B′,
BC=B′C′,
巩固练习
判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等; ( )
(2)一个锐角和这个角的邻边对应相等; ( )
(3)一个锐角和斜边对应相等; ( )
(4)两直角边对应相等; ( )
(5)一条直角边和斜边对应相等 ( )
HL
AAS或ASA
SAS
AAS
AAS
判一判
典例精讲
例1 如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD.
证明: ∵ AC⊥BC, BD⊥AD, ∴∠C与∠D都是直角.
AB=BA,
AC=BD .
在 Rt△ABC 和Rt△BAD 中,
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD.
A
B
D
C
归纳概念
新知归纳
已知条件 可选择的判定方法 需寻找的条件
一锐角对应相等
斜边对应相等
一直角边对应相等
直角三角形全等方法大归纳
ASA或AAS
可证直角与已知锐角的夹边对应相等或者与锐角(或直角)的对边对应相等
HL或AAS
可证一直角边对应相等或证一锐角对应相等
HL或ASA或AAS
可证斜边对应相等或证已知边相邻的锐角对应相等或证已知边所对的锐角对应相等
A'
B'
C'
A
B
C
课堂练习
1.下列说法不正确的是( )
A.两条直角边对应相等的两个直角三角形全等
B.一锐角和斜边对应相等的两个直角三角形全等
C.斜边和一直角边对应相等的两个直角三角形全等
D.有两边相等的两个直角三角形全等
D
2. 如图,在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE.求证:△EBC≌△DCB.
A
B
C
E
D
证明: ∵ BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中,
CE=BD,
BC=CB .
∴ Rt△EBC≌Rt△DCB (HL).
典例讲解
3.如图,有两个长度相同的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系?为什么?
解:在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF .
∴ Rt△ABC≌Rt△DEF (HL).
∵ ∠DEF+∠F=90°,
∴∠B+∠F=90°.
4.已知:如图,在△ABC和△DEF中,AP、DQ分别是高,并且
AB=DE,AP=DQ,∠BAC=∠EDF,求证:△ABC≌△DEF
A
C
P
D
E
F
Q
B
证明:∵AP、DQ是△ABC和△DEF的高
∴∠APB=∠DQE=90°
在Rt△ABP和Rt△DEQ中
AB=DE
AP=DQ
∴Rt△ABP≌Rt△DEQ (HL)
∴ ∠B=∠E
在△ABC和△DEF中
∠BAC=∠EDF
AB=DE
∠B=∠E
∴△ABC≌△DEF (ASA)
课堂总结
“斜边、直角边”
内容
斜边和一条直角边对应相等的两个直角三角形全等.
前提条件
在直角三角形中
使用方法
只须找除直角外的两个条件即可(两个条件中至少有一个条件是一对对应边相等)
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
