13.3.1 第1课时 等腰三角形的性质 课件(共21张PPT)
文档属性
| 名称 | 13.3.1 第1课时 等腰三角形的性质 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1017.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 17:43:35 | ||
图片预览




文档简介
(共21张PPT)
13.3.1 第1课时
等腰三角形的性质
人教版 八年级上册
教学目标
【教学目标】
1.知识与技能
(1)理解并掌握等腰三角形的判定定理及推论;
(2)能利用其性质与判定证明线段或角的相等关系。
2.过程与方法
(1)通过实践、观察、证明等腰三角形的性质,培养学生的推理能力;
(2)通过运用等腰三角形的性质解决有关的问题,提高运用知识和技能解决问题的能力。
3.情感态度和价值观
在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心。
【重点】等腰三角形的性质及应用。
【难点】等腰三角形性质的探究及证明。
复习旧知
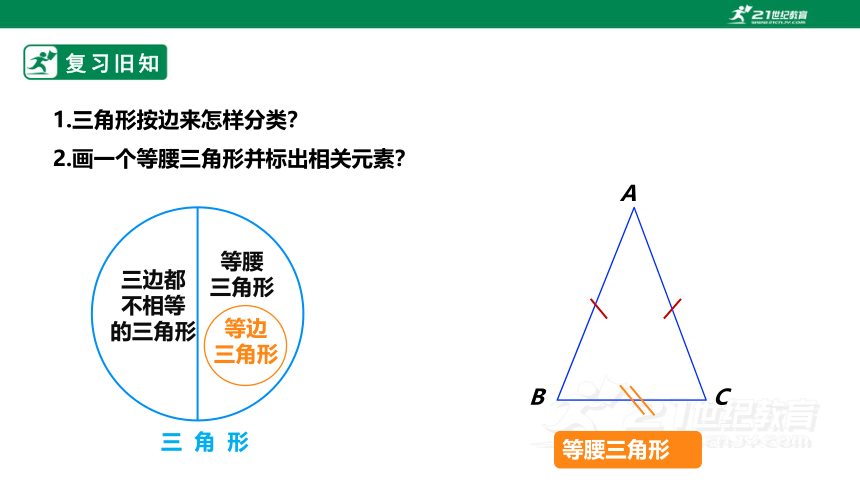
1.三角形按边来怎样分类?
2.画一个等腰三角形并标出相关元素?
三角形
三边都
不相等
的三角形
等腰
三角形
等边
三角形
等腰三角形
A
C
B
新知探究
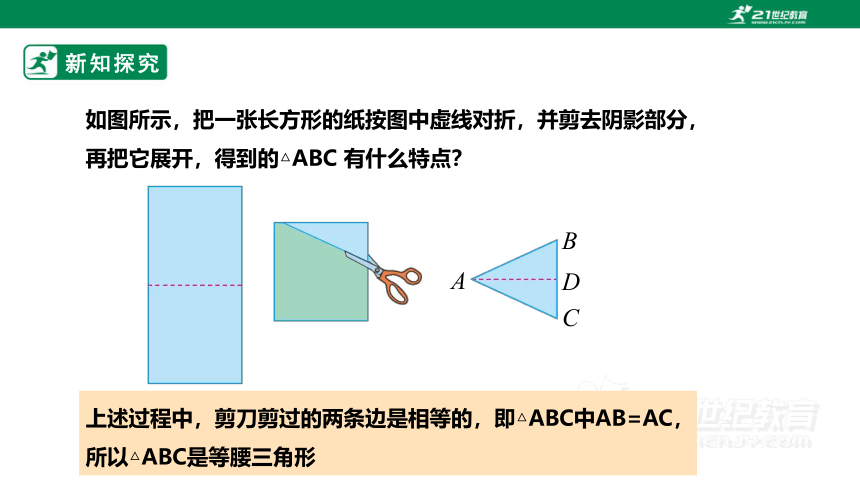
如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC 有什么特点?
A
B
C
D
上述过程中,剪刀剪过的两条边是相等的,即△ABC中AB=AC,所以△ABC是等腰三角形
新知探究
C
B
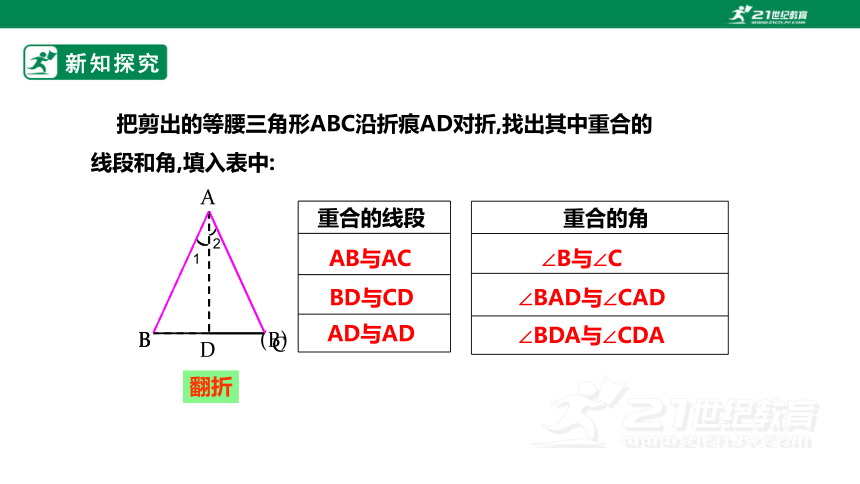
把剪出的等腰三角形ABC沿折痕AD对折,找出其中重合的线段和角,填入表中:
重合的角
重合的线段
∠B与∠C
∠BAD与∠CAD
∠BDA与∠CDA
(B)
A
B
D
翻折
BD与CD
AB与AC
AD与AD
1
2
新知探究
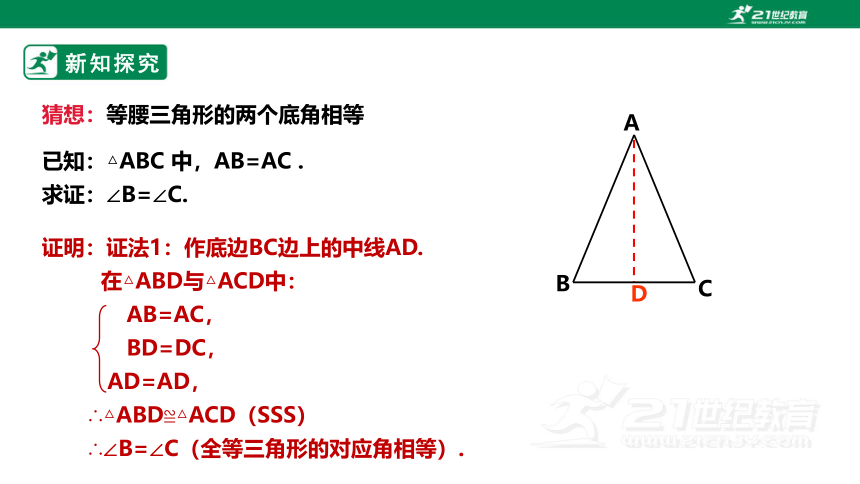
猜想:等腰三角形的两个底角相等
A
B
C
D
已知:△ABC 中,AB=AC .
求证:∠B=∠C.
证明:证法1:作底边BC边上的中线AD.
在△ABD与△ACD中:
AB=AC,
BD=DC,
AD=AD,
∴△ABD≌△ACD(SSS)
∴∠B=∠C(全等三角形的对应角相等).
新知探究
证法2:作顶角∠BAC的平分线AD,交BC于点D.
∵AD平分∠BAC ,
∴∠1=∠2.
在△ABD与△ACD中,
AB=AC(已知),
∠1=∠2(已证),
AD=AD(公共边),
∴ △ABD ≌ △ACD(SAS),
∴ ∠B=∠C.
A
B
C
D
1 2
新知探究
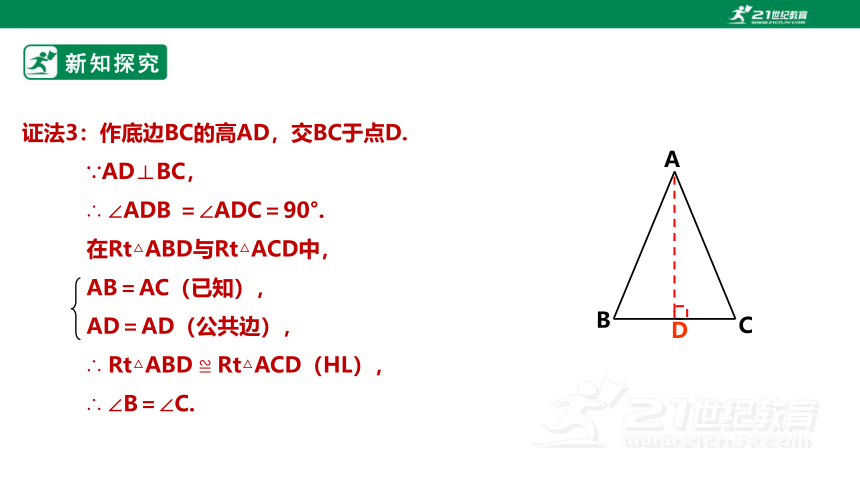
证法3:作底边BC的高AD,交BC于点D.
∵AD⊥BC,
∴ ∠ADB =∠ADC=90°.
在Rt△ABD与Rt△ACD中,
AB=AC(已知),
AD=AD(公共边),
∴ Rt△ABD ≌ Rt△ACD(HL),
∴ ∠B=∠C.
D
A
B
C
总结归纳
等腰三角形的两个底角相等.
简称:等边对等角
性质1
符号语言:
在△ABC中
∵ AC=AB(已知)
∴ ∠B=∠C(等边对等角)
新知探究
A
B
D
C
猜想:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。
新知探究
③作∠A的角平分线AD
∴∠BAD=∠CAD
在△ABD和△ACD 中 AB=AC ∠BAD=∠CAD AD=AD ∴△ABD≌△ACD (SAS)
∴BD=CD,∠ADB=∠ADC=90
∴AD是BC边上的中线,
也是底边BC上的高
①作BC上的中线AD
∴BD=CD
在△ABD和△ACD中
AB=AC
AD=AD
BD=CD
∴△ABD≌△ACD (SSS)
∴∠BAD=∠CAD,
∠ADB=∠ADC=90°
∴AD是∠BAC的平分线,
也是BC边上的高
②作AD⊥BC,垂足为D
∴ ∠ABD=∠ADC=90°
在△ABD和△ACD中
AB=AC
BD=CD
∴△ABD≌△ACD (HL)
∴BD=CD,
∠BAD=∠CAD
∴AD是BC边上的中线,
也是∠BAC的平分线
证明:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。
A
B
D
C
归纳总结
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
简称:三线合一
性质2
(1)∵AB=AC,AD平分∠BAC
∴BD=CD,AD⊥BC.
(2)∵AB=AC,BD=CD
∴AD平分∠BAC,AD⊥BC.
(3)∵AB=AC, AD⊥BC
∴ AD平分∠BAC ,BD=CD.
符号语言:
例题讲解
例1.在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ ABC各角的度数。
把∠A设为x的话,那么∠ABC,∠C 都可以用x来表示,这样过程就更简捷了.
解析:根据等边对等角的性质,我们可以得到∠A=∠ABD,∠ABC=∠C=∠BDC,
由∠BDC=∠A+∠ABD,就可得到∠ABC=∠C=∠BDC=2∠A.
再由三角形内角和为180°,就可求出△ABC 的三个内角.
例题讲解
解:AB=AC,BD=BC=AD,
∠ ABC= ∠ C= ∠ BDC
∠ A= ∠ ADD(等边对等角)
设A=x,则
∠ BDC= ∠ A+ ∠ ABD=2x
从而∠ ABC= ∠ C= ∠ BDC=2x
于是在△ ABC中,有
∠ A+ ∠ ABC+ ∠ C=x+2x+2x=1800.
解得x=360
在△ ABC中, ∠ A=360 ∠ABC= ∠ C=720
B
C
A
D
课堂练习
1.如图,在△ABC中,已知AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )
A.35° B.45° C.55° D.60°
C
2.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.
取AB边上的中点E,连接DE,则∠ADE =_______.
54°
课堂练习
4.已知:如图,在△ABC中,点D在边BC上,AB=AD=DC,∠C=35°,则∠BAD=________度.
40
3.如图,在△ABC中,AB=AC,BD平分∠ABC,BD=BE,∠A=100°,则∠DEC=( )
A.90° B.100° C.105° D.110°
B
5. 在等腰△ABC中,AB=AC,∠A=108°,那么∠B= ,∠C= ,一腰上的高与另一腰的夹角为 .
36°
36°
18°
课堂练习
解:∵AB=AC=CD,
∴∠B=∠C,∠1=∠2.
∵BD=AD,
∴∠B=∠3.
∵∠1=∠B+∠3,∠B+∠3+∠2+∠C=180°,
∴∠B=36°,∠C=36°,∠BAC=108°.
6.如图,在△ABC中,点D在BC上,且有AB=AC=CD,BD=AD,求△ABC中各内角的度数.
1
3
2
A
B
C
D
课堂练习
7.如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
解:∵AB=AD=DC,
∴ ∠B= ∠ADB,∠C= ∠DAC.
设 ∠C=x,则 ∠DAC=x,
∠B= ∠ADB= ∠C+ ∠DAC=2x,
在△ABC中, 根据三角形内角和定理,得
2x+x+26°+x=180°,
解得x=38.5°.
∴ ∠C= x=38.5°, ∠B=2x=77°.
课堂小结
等腰三角形的性质
边
两腰相等
三线合一
三线
角
等边对等角
证边相等
证角相等
对称轴
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.3.1 第1课时
等腰三角形的性质
人教版 八年级上册
教学目标
【教学目标】
1.知识与技能
(1)理解并掌握等腰三角形的判定定理及推论;
(2)能利用其性质与判定证明线段或角的相等关系。
2.过程与方法
(1)通过实践、观察、证明等腰三角形的性质,培养学生的推理能力;
(2)通过运用等腰三角形的性质解决有关的问题,提高运用知识和技能解决问题的能力。
3.情感态度和价值观
在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心。
【重点】等腰三角形的性质及应用。
【难点】等腰三角形性质的探究及证明。
复习旧知
1.三角形按边来怎样分类?
2.画一个等腰三角形并标出相关元素?
三角形
三边都
不相等
的三角形
等腰
三角形
等边
三角形
等腰三角形
A
C
B
新知探究
如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC 有什么特点?
A
B
C
D
上述过程中,剪刀剪过的两条边是相等的,即△ABC中AB=AC,所以△ABC是等腰三角形
新知探究
C
B
把剪出的等腰三角形ABC沿折痕AD对折,找出其中重合的线段和角,填入表中:
重合的角
重合的线段
∠B与∠C
∠BAD与∠CAD
∠BDA与∠CDA
(B)
A
B
D
翻折
BD与CD
AB与AC
AD与AD
1
2
新知探究
猜想:等腰三角形的两个底角相等
A
B
C
D
已知:△ABC 中,AB=AC .
求证:∠B=∠C.
证明:证法1:作底边BC边上的中线AD.
在△ABD与△ACD中:
AB=AC,
BD=DC,
AD=AD,
∴△ABD≌△ACD(SSS)
∴∠B=∠C(全等三角形的对应角相等).
新知探究
证法2:作顶角∠BAC的平分线AD,交BC于点D.
∵AD平分∠BAC ,
∴∠1=∠2.
在△ABD与△ACD中,
AB=AC(已知),
∠1=∠2(已证),
AD=AD(公共边),
∴ △ABD ≌ △ACD(SAS),
∴ ∠B=∠C.
A
B
C
D
1 2
新知探究
证法3:作底边BC的高AD,交BC于点D.
∵AD⊥BC,
∴ ∠ADB =∠ADC=90°.
在Rt△ABD与Rt△ACD中,
AB=AC(已知),
AD=AD(公共边),
∴ Rt△ABD ≌ Rt△ACD(HL),
∴ ∠B=∠C.
D
A
B
C
总结归纳
等腰三角形的两个底角相等.
简称:等边对等角
性质1
符号语言:
在△ABC中
∵ AC=AB(已知)
∴ ∠B=∠C(等边对等角)
新知探究
A
B
D
C
猜想:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。
新知探究
③作∠A的角平分线AD
∴∠BAD=∠CAD
在△ABD和△ACD 中 AB=AC ∠BAD=∠CAD AD=AD ∴△ABD≌△ACD (SAS)
∴BD=CD,∠ADB=∠ADC=90
∴AD是BC边上的中线,
也是底边BC上的高
①作BC上的中线AD
∴BD=CD
在△ABD和△ACD中
AB=AC
AD=AD
BD=CD
∴△ABD≌△ACD (SSS)
∴∠BAD=∠CAD,
∠ADB=∠ADC=90°
∴AD是∠BAC的平分线,
也是BC边上的高
②作AD⊥BC,垂足为D
∴ ∠ABD=∠ADC=90°
在△ABD和△ACD中
AB=AC
BD=CD
∴△ABD≌△ACD (HL)
∴BD=CD,
∠BAD=∠CAD
∴AD是BC边上的中线,
也是∠BAC的平分线
证明:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。
A
B
D
C
归纳总结
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
简称:三线合一
性质2
(1)∵AB=AC,AD平分∠BAC
∴BD=CD,AD⊥BC.
(2)∵AB=AC,BD=CD
∴AD平分∠BAC,AD⊥BC.
(3)∵AB=AC, AD⊥BC
∴ AD平分∠BAC ,BD=CD.
符号语言:
例题讲解
例1.在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ ABC各角的度数。
把∠A设为x的话,那么∠ABC,∠C 都可以用x来表示,这样过程就更简捷了.
解析:根据等边对等角的性质,我们可以得到∠A=∠ABD,∠ABC=∠C=∠BDC,
由∠BDC=∠A+∠ABD,就可得到∠ABC=∠C=∠BDC=2∠A.
再由三角形内角和为180°,就可求出△ABC 的三个内角.
例题讲解
解:AB=AC,BD=BC=AD,
∠ ABC= ∠ C= ∠ BDC
∠ A= ∠ ADD(等边对等角)
设A=x,则
∠ BDC= ∠ A+ ∠ ABD=2x
从而∠ ABC= ∠ C= ∠ BDC=2x
于是在△ ABC中,有
∠ A+ ∠ ABC+ ∠ C=x+2x+2x=1800.
解得x=360
在△ ABC中, ∠ A=360 ∠ABC= ∠ C=720
B
C
A
D
课堂练习
1.如图,在△ABC中,已知AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )
A.35° B.45° C.55° D.60°
C
2.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.
取AB边上的中点E,连接DE,则∠ADE =_______.
54°
课堂练习
4.已知:如图,在△ABC中,点D在边BC上,AB=AD=DC,∠C=35°,则∠BAD=________度.
40
3.如图,在△ABC中,AB=AC,BD平分∠ABC,BD=BE,∠A=100°,则∠DEC=( )
A.90° B.100° C.105° D.110°
B
5. 在等腰△ABC中,AB=AC,∠A=108°,那么∠B= ,∠C= ,一腰上的高与另一腰的夹角为 .
36°
36°
18°
课堂练习
解:∵AB=AC=CD,
∴∠B=∠C,∠1=∠2.
∵BD=AD,
∴∠B=∠3.
∵∠1=∠B+∠3,∠B+∠3+∠2+∠C=180°,
∴∠B=36°,∠C=36°,∠BAC=108°.
6.如图,在△ABC中,点D在BC上,且有AB=AC=CD,BD=AD,求△ABC中各内角的度数.
1
3
2
A
B
C
D
课堂练习
7.如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
解:∵AB=AD=DC,
∴ ∠B= ∠ADB,∠C= ∠DAC.
设 ∠C=x,则 ∠DAC=x,
∠B= ∠ADB= ∠C+ ∠DAC=2x,
在△ABC中, 根据三角形内角和定理,得
2x+x+26°+x=180°,
解得x=38.5°.
∴ ∠C= x=38.5°, ∠B=2x=77°.
课堂小结
等腰三角形的性质
边
两腰相等
三线合一
三线
角
等边对等角
证边相等
证角相等
对称轴
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
