13.3.1 第2课时 等腰三角形的判定 课件(共17张PPT)
文档属性
| 名称 | 13.3.1 第2课时 等腰三角形的判定 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 995.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 17:44:03 | ||
图片预览





文档简介
(共17张PPT)
13.3.1 第2课时
等腰三角形的判定
人教版 八年级上册
教学目标
【教学目标】
1.知识与技能
(1)理解并掌握等腰三角形的判定定理及推论;
(2)能利用其性质与判定证明线段或角的相等关系。
2.过程与方法
(1)通过实践、观察、证明等腰三角形的性质,培养学生的推理能力;
(2)通过运用等腰三角形的性质解决有关的问题,提高运用知识和技能解决问题的能力。
3.情感态度和价值观
在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心。
【重点】等腰三角形的性质及应用。
【难点】等腰三角形性质的探究及证明。
性质1:等腰三角形的两个底角相等
(简写成:等边对等角).
A
B
C
应用格式:
∵ AB=AC,
∴ ∠B=∠C(等边对等角).
复习回顾
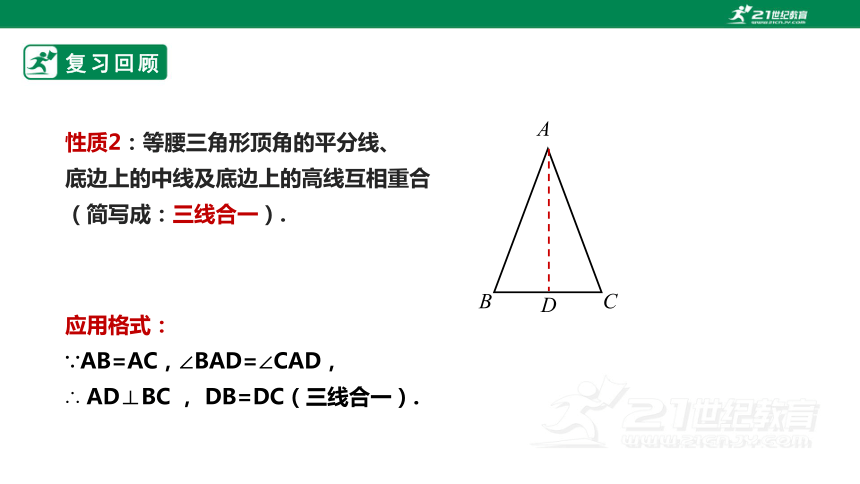
性质2:等腰三角形顶角的平分线、
底边上的中线及底边上的高线互相重合(简写成:三线合一).
A
B
C
D
应用格式:
∵AB=AC,AD⊥BC,
∴BD=CD, ∠BAD=∠CAD(三线合一).
复习回顾
性质2:等腰三角形顶角的平分线、
底边上的中线及底边上的高线互相重合(简写成:三线合一).
应用格式:
∵AB=AC,BD=CD,
∴ AD⊥BC , ∠BAD=∠CAD(三线合一).
A
B
C
D
复习回顾
性质2:等腰三角形顶角的平分线、
底边上的中线及底边上的高线互相重合(简写成:三线合一).
A
B
C
D
应用格式:
∵AB=AC,∠BAD=∠CAD,
∴ AD⊥BC , DB=DC(三线合一).
复习回顾
新知探究
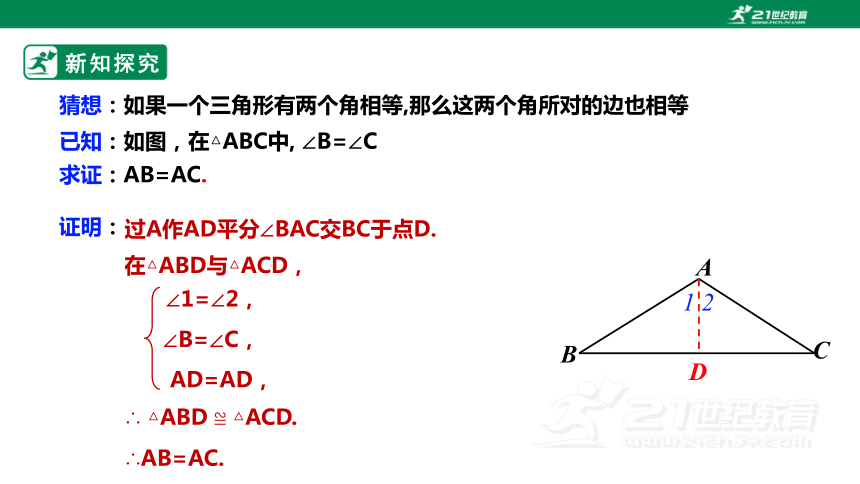
猜想:如果一个三角形有两个角相等,那么这两个角所对的边也相等
已知:如图,在△ABC中, ∠B=∠C
求证:AB=AC.
在△ABD与△ACD,
∠1=∠2,
∴ △ABD ≌ △ACD.
∠B=∠C,
AD=AD,
∴AB=AC.
过A作AD平分∠BAC交BC于点D.
证明:
C
A
B
2
1
D
∴ AC=AB. (等角对等边)
即△ABC为等腰三角形.
∵∠B=∠C,(已知)
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角对等边”).
应用格式:
B
C
A
(
(
等腰三角形的判定方法:
在△ABC中,
归纳总结
例题讲解
例2 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
分析:
从求证看:要证AB=AC,需证∠B=∠C,
从已知看:因为∠1=∠2,AD∥BC
可以找出∠B,∠C与的关系。
A
B
C
D
E
1
2
例题讲解
证明:
∵AD∥BC,
A
B
C
D
E
1
2
∴∠1=∠B(两直线平行, 同位角相等),
∠2=∠C(两直线平行,内错角相等)。
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等边对等角)
例题讲解
例3 已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形。
作法: (1) 作线段AB=a。
(2)作线段AB的垂直平分线MN,与AB相交于点D.
(3)在MN上取一点C,使DC=h。
(4)连接AC、BC,则ABC就是所求作的等腰三角形。
D
C
A
B
M
N
2.一个三角形的一个外角为130°,且它恰好等于一个不相邻的内角的2倍.这个三角形是( )
A.钝角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
1.如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )
A.5个 B.4个 C.3个 D.2个
课堂练习
C
A
3.在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是( )
A. ∠A=50°,∠B=70° B. ∠A=70°,∠B=40°
C. ∠A=30°,∠B=90° D. ∠A=80°,∠B=60°
B
4.如图,已知OC平分∠AOB,CD∥OB,若OD=3 cm,则CD等于______.
3 cm
课堂练习
5.如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
B
C
A
D
E
解:是等腰三角形,其理由如下
由折叠可知,∠EBD=∠CBD.
∵AD∥BC,∴∠EDB=∠CBD,
∴∠EDB=∠EBD,
∴BE=DE,
△EBD是等腰三角形.
课堂练习
课堂小结
等腰三角形
边
两腰相等
三线合一
三线
角
等边对等角
证边相等
证角相等
对称轴
性质
判定
边
两边相等
三线
角
等角对等边
证边相等
互逆
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.3.1 第2课时
等腰三角形的判定
人教版 八年级上册
教学目标
【教学目标】
1.知识与技能
(1)理解并掌握等腰三角形的判定定理及推论;
(2)能利用其性质与判定证明线段或角的相等关系。
2.过程与方法
(1)通过实践、观察、证明等腰三角形的性质,培养学生的推理能力;
(2)通过运用等腰三角形的性质解决有关的问题,提高运用知识和技能解决问题的能力。
3.情感态度和价值观
在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心。
【重点】等腰三角形的性质及应用。
【难点】等腰三角形性质的探究及证明。
性质1:等腰三角形的两个底角相等
(简写成:等边对等角).
A
B
C
应用格式:
∵ AB=AC,
∴ ∠B=∠C(等边对等角).
复习回顾
性质2:等腰三角形顶角的平分线、
底边上的中线及底边上的高线互相重合(简写成:三线合一).
A
B
C
D
应用格式:
∵AB=AC,AD⊥BC,
∴BD=CD, ∠BAD=∠CAD(三线合一).
复习回顾
性质2:等腰三角形顶角的平分线、
底边上的中线及底边上的高线互相重合(简写成:三线合一).
应用格式:
∵AB=AC,BD=CD,
∴ AD⊥BC , ∠BAD=∠CAD(三线合一).
A
B
C
D
复习回顾
性质2:等腰三角形顶角的平分线、
底边上的中线及底边上的高线互相重合(简写成:三线合一).
A
B
C
D
应用格式:
∵AB=AC,∠BAD=∠CAD,
∴ AD⊥BC , DB=DC(三线合一).
复习回顾
新知探究
猜想:如果一个三角形有两个角相等,那么这两个角所对的边也相等
已知:如图,在△ABC中, ∠B=∠C
求证:AB=AC.
在△ABD与△ACD,
∠1=∠2,
∴ △ABD ≌ △ACD.
∠B=∠C,
AD=AD,
∴AB=AC.
过A作AD平分∠BAC交BC于点D.
证明:
C
A
B
2
1
D
∴ AC=AB. (等角对等边)
即△ABC为等腰三角形.
∵∠B=∠C,(已知)
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角对等边”).
应用格式:
B
C
A
(
(
等腰三角形的判定方法:
在△ABC中,
归纳总结
例题讲解
例2 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
分析:
从求证看:要证AB=AC,需证∠B=∠C,
从已知看:因为∠1=∠2,AD∥BC
可以找出∠B,∠C与的关系。
A
B
C
D
E
1
2
例题讲解
证明:
∵AD∥BC,
A
B
C
D
E
1
2
∴∠1=∠B(两直线平行, 同位角相等),
∠2=∠C(两直线平行,内错角相等)。
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等边对等角)
例题讲解
例3 已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形。
作法: (1) 作线段AB=a。
(2)作线段AB的垂直平分线MN,与AB相交于点D.
(3)在MN上取一点C,使DC=h。
(4)连接AC、BC,则ABC就是所求作的等腰三角形。
D
C
A
B
M
N
2.一个三角形的一个外角为130°,且它恰好等于一个不相邻的内角的2倍.这个三角形是( )
A.钝角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
1.如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )
A.5个 B.4个 C.3个 D.2个
课堂练习
C
A
3.在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是( )
A. ∠A=50°,∠B=70° B. ∠A=70°,∠B=40°
C. ∠A=30°,∠B=90° D. ∠A=80°,∠B=60°
B
4.如图,已知OC平分∠AOB,CD∥OB,若OD=3 cm,则CD等于______.
3 cm
课堂练习
5.如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
B
C
A
D
E
解:是等腰三角形,其理由如下
由折叠可知,∠EBD=∠CBD.
∵AD∥BC,∴∠EDB=∠CBD,
∴∠EDB=∠EBD,
∴BE=DE,
△EBD是等腰三角形.
课堂练习
课堂小结
等腰三角形
边
两腰相等
三线合一
三线
角
等边对等角
证边相等
证角相等
对称轴
性质
判定
边
两边相等
三线
角
等角对等边
证边相等
互逆
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
