13.2 第1课时 作轴对称图形 课件(共19张PPT)
文档属性
| 名称 | 13.2 第1课时 作轴对称图形 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 17:42:33 | ||
图片预览





文档简介
(共19张PPT)
13.2 第1课时 作轴对称图形
人教版 八年级上册
教学目标
【教学目标】
1.知识与技能:
(1)通过实际操作,了解什么叫做轴对称变换。
(2)如何作出一个图形关于一条直线的轴对称图形。
(3)探究并归纳已知点关于坐标轴对称的点的坐标变化规律。
2.过程与方法:通过观察、操作、交流等活动发展空间观念和推理能力。
3.情感态度和价值观:通过师生共同活动,促进学生在学习活动中培养良好的情感,合作交流,主动参与的意识,在独立思考的同时能够认同他人。
【教学重点】(1)画轴对称图形。
(2)在平面直角坐标系中关于x轴或y轴对称的点的坐标的变化规律和作出与一个图形关于x轴或y轴对称的图形。
【教学难点】点的坐标变换规律的灵活运用
回顾复习
1.线段的垂直平分的性质:
线段的垂直平分线上的点到线段的两个端点的距离相等
作用:见垂直平分线,得线段相等
2.线段的垂直平分的判定:
到线段的两个端点距离相等的点在线段的垂直平分线上
作用:判断一个点是否在线段的垂直平分线上
新知探索
探究:轴对称变换
l
P
P'
(1)观察,这个图中两上小猪是什么关系?
(2)对称轴是折痕所在的直线,即直线l,它与图中的线段PP ′是什么关系?
总结归纳
轴对称的性质
由一个平面图形可以得到与它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全相同;
新图形上的每一点都是原图形上的某一点关于直线l的对称点;
连接任意一对对应点的线段被对称轴垂直平分.
新知探索
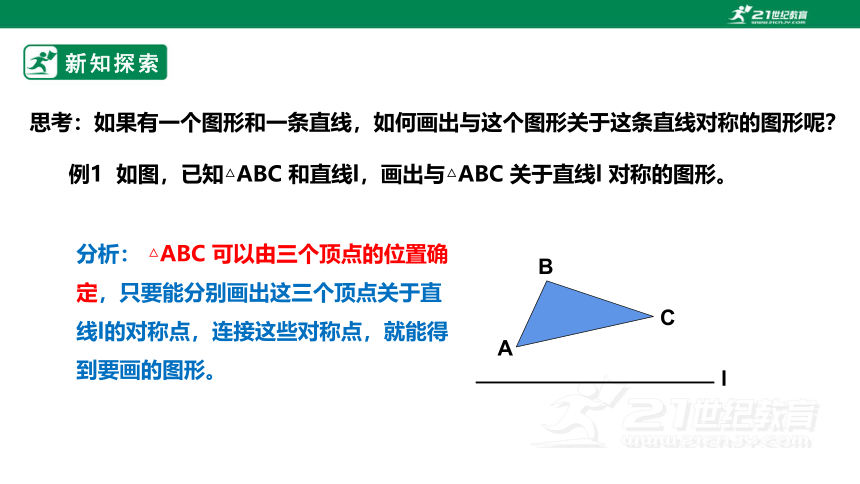
例1 如图,已知△ABC 和直线l,画出与△ABC 关于直线l 对称的图形。
B
A
C
l
分析: △ABC 可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形。
思考:如果有一个图形和一条直线,如何画出与这个图形关于这条直线对称的图形呢?
新知探索
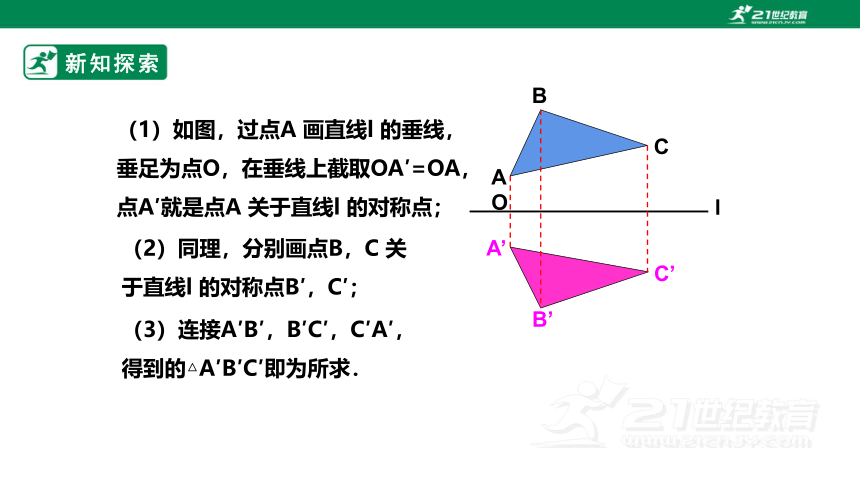
(1)如图,过点A 画直线l 的垂线,垂足为点O,在垂线上截取OA′=OA,点A′就是点A 关于直线l 的对称点;
B
A
C
l
A’
B’
C’
O
(2)同理,分别画点B,C 关于直线l 的对称点B′,C′;
(3)连接A′B′,B′C′,C′A′,得到的△A′B′C′即为所求.
新知探索
几何图形都可以看作由点组成,对于某些图形,只要画出图形中的一些特殊点的对称点,连接对称点,就可以得到原图形的轴对称图形。
想一想
由例1,你能总结出经验吗?
总结归纳
画轴对称图形的步骤
画轴对称图形要经历一找二作三连这三个步骤:
(1)找:在原图形上找特殊点(如线段的端点);
(2)作:作各个特殊点关于对称轴的对称点;
(3)连:按原图的顺序连接所作的各对称点.
课堂练习
1.下列各图分别以直线l为对称轴,所作轴对称图形错误的是( )
C
课堂练习
2.如图所示,将一个正方形纸片按下列顺序折叠,然 后将最后折叠的纸片沿虚线剪去一个三角形和一个 形 如“ ”的图形,将纸片展开,得到的图形是( )
D
课堂练习
3.如图,将长方形ABCD沿DE折叠,使A点落在BC上的F处,若∠EFB=50°,则∠CFD的度数为( )
A.20°
B.30°
C.40°
D.50°
C
课堂练习
4.如图,在3×3的方格图中,再将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,方法有( )
A.1种 B.2种 C.3种 D.4种
C
课堂练习
5.如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′两点处,若∠AOB′=70°,则∠B′OG的度数为________.
55°
课堂练习
6.如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC.
(1)在图中作出△ABC关于直线l对称的
△A1B1C1;
(2)在(1)问的结果下,连接BB1,CC1,
求四边形BB1C1C的面积.
解:(1)如图,△A1B1C1为所求;
(2)连接BB1,CC1.
S四边形BB1C1C=(2+4)×4÷2=12
课堂练习
7.如图,C、D、E、F是一个长方形台球桌的4个顶点,A、B是桌面上的两个球,怎样击打A球,才能使A球撞击桌面边缘CF后反弹能够撞击B球 请画出A球经过的路线,并写出作法.
解:如图,作点A关于直线CF对称的点A',连接A' B交CF于点P,则点P即为A球撞击桌面边缘CF的位置.连接AP,折线APB即为A球经过的路线.
课堂小结
画
轴
对
称
图
形
作图原理
作图方法
对称轴是对称点连线段的垂直平分线.
作垂线、取相等、连图形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.2 第1课时 作轴对称图形
人教版 八年级上册
教学目标
【教学目标】
1.知识与技能:
(1)通过实际操作,了解什么叫做轴对称变换。
(2)如何作出一个图形关于一条直线的轴对称图形。
(3)探究并归纳已知点关于坐标轴对称的点的坐标变化规律。
2.过程与方法:通过观察、操作、交流等活动发展空间观念和推理能力。
3.情感态度和价值观:通过师生共同活动,促进学生在学习活动中培养良好的情感,合作交流,主动参与的意识,在独立思考的同时能够认同他人。
【教学重点】(1)画轴对称图形。
(2)在平面直角坐标系中关于x轴或y轴对称的点的坐标的变化规律和作出与一个图形关于x轴或y轴对称的图形。
【教学难点】点的坐标变换规律的灵活运用
回顾复习
1.线段的垂直平分的性质:
线段的垂直平分线上的点到线段的两个端点的距离相等
作用:见垂直平分线,得线段相等
2.线段的垂直平分的判定:
到线段的两个端点距离相等的点在线段的垂直平分线上
作用:判断一个点是否在线段的垂直平分线上
新知探索
探究:轴对称变换
l
P
P'
(1)观察,这个图中两上小猪是什么关系?
(2)对称轴是折痕所在的直线,即直线l,它与图中的线段PP ′是什么关系?
总结归纳
轴对称的性质
由一个平面图形可以得到与它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全相同;
新图形上的每一点都是原图形上的某一点关于直线l的对称点;
连接任意一对对应点的线段被对称轴垂直平分.
新知探索
例1 如图,已知△ABC 和直线l,画出与△ABC 关于直线l 对称的图形。
B
A
C
l
分析: △ABC 可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形。
思考:如果有一个图形和一条直线,如何画出与这个图形关于这条直线对称的图形呢?
新知探索
(1)如图,过点A 画直线l 的垂线,垂足为点O,在垂线上截取OA′=OA,点A′就是点A 关于直线l 的对称点;
B
A
C
l
A’
B’
C’
O
(2)同理,分别画点B,C 关于直线l 的对称点B′,C′;
(3)连接A′B′,B′C′,C′A′,得到的△A′B′C′即为所求.
新知探索
几何图形都可以看作由点组成,对于某些图形,只要画出图形中的一些特殊点的对称点,连接对称点,就可以得到原图形的轴对称图形。
想一想
由例1,你能总结出经验吗?
总结归纳
画轴对称图形的步骤
画轴对称图形要经历一找二作三连这三个步骤:
(1)找:在原图形上找特殊点(如线段的端点);
(2)作:作各个特殊点关于对称轴的对称点;
(3)连:按原图的顺序连接所作的各对称点.
课堂练习
1.下列各图分别以直线l为对称轴,所作轴对称图形错误的是( )
C
课堂练习
2.如图所示,将一个正方形纸片按下列顺序折叠,然 后将最后折叠的纸片沿虚线剪去一个三角形和一个 形 如“ ”的图形,将纸片展开,得到的图形是( )
D
课堂练习
3.如图,将长方形ABCD沿DE折叠,使A点落在BC上的F处,若∠EFB=50°,则∠CFD的度数为( )
A.20°
B.30°
C.40°
D.50°
C
课堂练习
4.如图,在3×3的方格图中,再将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,方法有( )
A.1种 B.2种 C.3种 D.4种
C
课堂练习
5.如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′两点处,若∠AOB′=70°,则∠B′OG的度数为________.
55°
课堂练习
6.如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC.
(1)在图中作出△ABC关于直线l对称的
△A1B1C1;
(2)在(1)问的结果下,连接BB1,CC1,
求四边形BB1C1C的面积.
解:(1)如图,△A1B1C1为所求;
(2)连接BB1,CC1.
S四边形BB1C1C=(2+4)×4÷2=12
课堂练习
7.如图,C、D、E、F是一个长方形台球桌的4个顶点,A、B是桌面上的两个球,怎样击打A球,才能使A球撞击桌面边缘CF后反弹能够撞击B球 请画出A球经过的路线,并写出作法.
解:如图,作点A关于直线CF对称的点A',连接A' B交CF于点P,则点P即为A球撞击桌面边缘CF的位置.连接AP,折线APB即为A球经过的路线.
课堂小结
画
轴
对
称
图
形
作图原理
作图方法
对称轴是对称点连线段的垂直平分线.
作垂线、取相等、连图形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
