第十八章 平行四边形单元质量评估试题(含答案)
文档属性
| 名称 | 第十八章 平行四边形单元质量评估试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 175.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 20:55:15 | ||
图片预览



文档简介
第十八章 平行四边形本章质量评估 (时间:90分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列说法中,正确的是 ( )
A.相等的角一定是对顶角
B.四个角都相等的四边形一定是正方形
C.平行四边形的对角线互相平分
D.矩形的对角线一定互相垂直
2.如图,△ABC中,D,E分别是边AB,AC的中点.若DE=2,则BC等于 ( )
A.2 B.3 C.4 D.5
3.如图,在 ABCD中,BM是∠ABC的平分线,交CD于点M,且MC=2, ABCD的周长是14,则DM等于 ( )
A.1 B.2 C.3 D.4
4.在 ABCD中,AC,BD是对角线,如果添加一个条件,即可推出 ABCD是矩形,那么这个条件是 ( )
A.AB=BC B.AC=BD
C.AC⊥BD D.AB⊥BD
5.如图,在菱形ABCD中,对角线AC,BD相交于点O,H为AD的中点,菱形ABCD的周长为28,则OH的长等于 ( )
A.3.5 B.4 C.7 D.14
6.如图所示,∠MON=90°,矩形ABCD的顶点A,B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1.运动过程中,点D到点O的最大距离为( )
A.+1 B. C. D.
7.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于 ( )
A.50° B.60° C.70° D.80°
8.如图,在正方形ABCD的外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为 ( )
A.45° B.55° C.60° D.75°
9.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B'处,点A落在点A'处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是 ( )
A.12 B.24 C.12 D.16
10.如图,正方形 ABCD中,点E,F 分别在 BC,CD上,△AEF是等边三角形,连接AC 交 EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC 垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE .其中正确的结论有 ( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题4分,共32分)
11.如图,在四边形ABCD中,对角线AC,BD交于点O,AD∥BC,请添加一个条件: ,使四边形ABCD为平行四边形(不添加任何辅助线).
12.将矩形ABCD沿AE折叠,得到如图所示的图形.已知∠CEB'=50°,则∠AEB'= °.
13.如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED的度数为 .
14.如图,菱形ABCD中,E,F分别是BC,CD的中点,过点E作EG⊥AD于G,连接EF,GF,若∠A=80°,则∠DGF的度数为 .
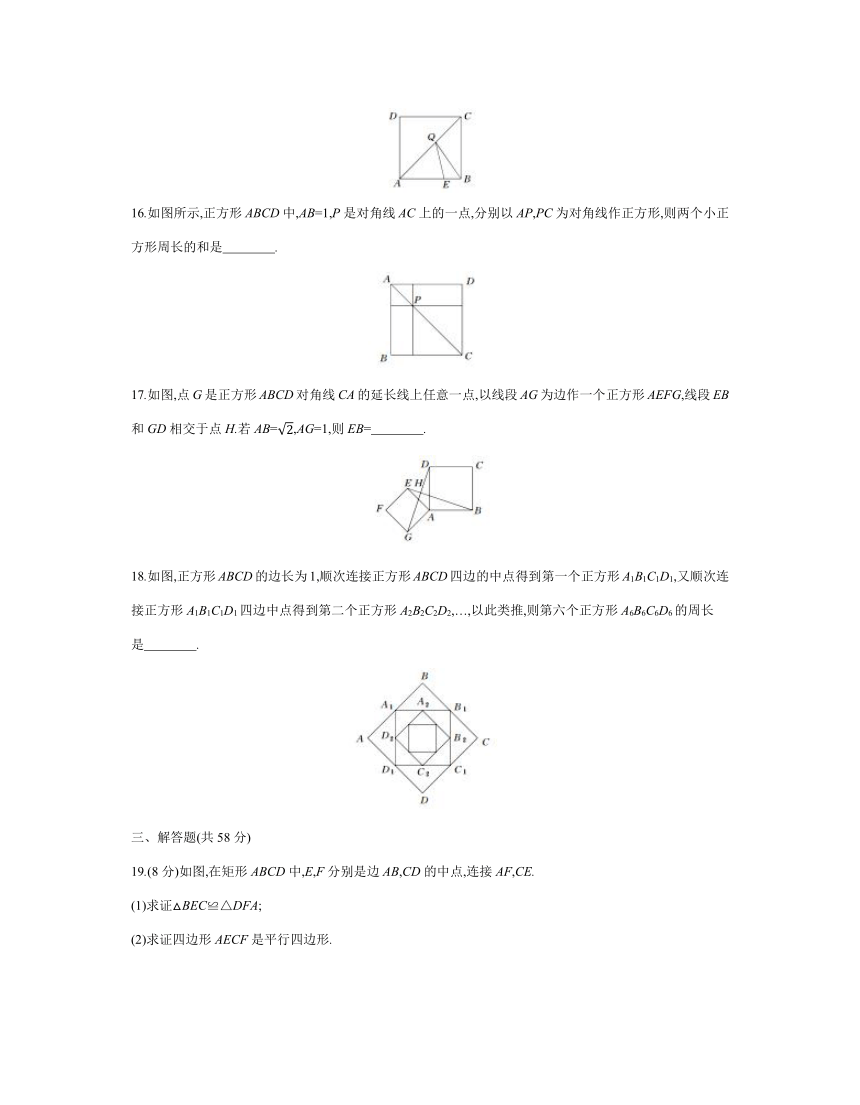
15.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为 .
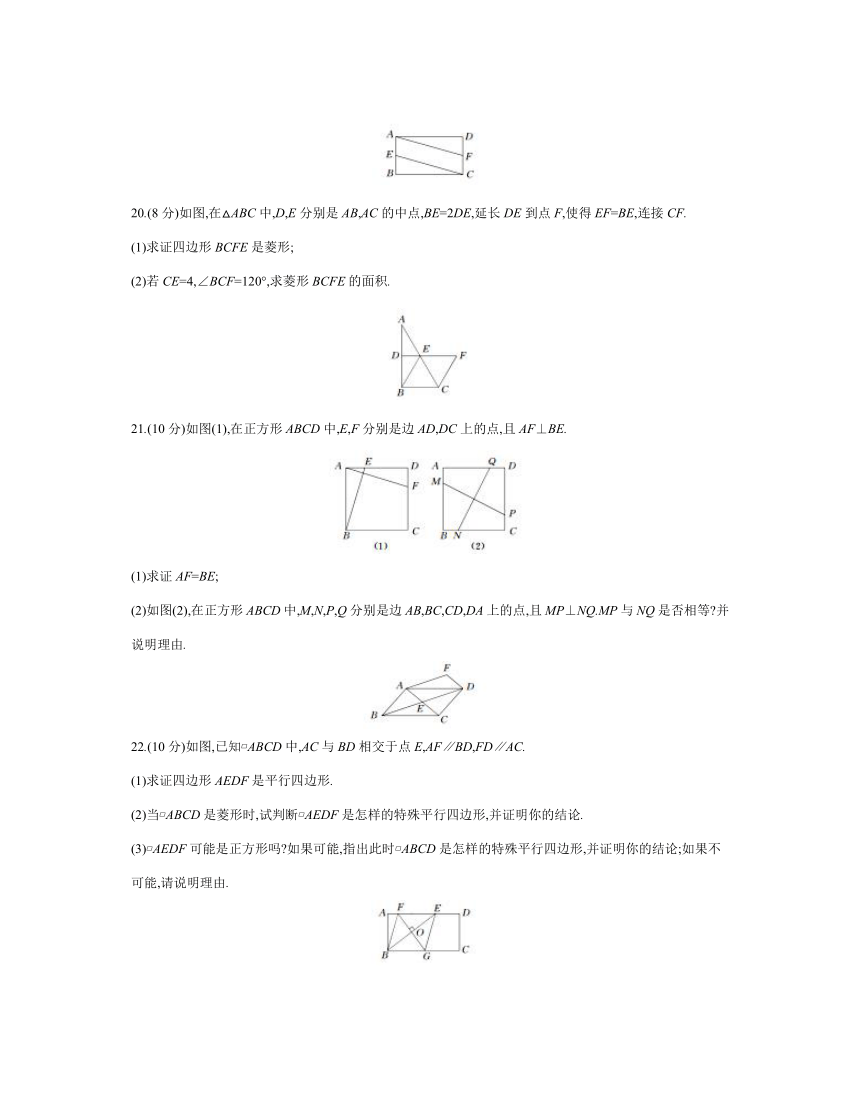
16.如图所示,正方形ABCD中,AB=1,P是对角线AC上的一点,分别以AP,PC为对角线作正方形,则两个小正方形周长的和是 .
17.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=,AG=1,则EB= .
18.如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,又顺次连接正方形A1B1C1D1四边中点得到第二个正方形A2B2C2D2,…,以此类推,则第六个正方形A6B6C6D6的周长是 .
三、解答题(共58分)
19.(8分)如图,在矩形ABCD中,E,F分别是边AB,CD的中点,连接AF,CE.
(1)求证△BEC≌△DFA;
(2)求证四边形AECF是平行四边形.
20.(8分)如图,在△ABC中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
21.(10分)如图(1),在正方形ABCD中,E,F分别是边AD,DC上的点,且AF⊥BE.
(1)求证AF=BE;
(2)如图(2),在正方形ABCD中,M,N,P,Q分别是边AB,BC,CD,DA上的点,且MP⊥NQ.MP与NQ是否相等 并说明理由.
22.(10分)如图,已知 ABCD中,AC与BD相交于点E,AF∥BD,FD∥AC.
(1)求证四边形AEDF是平行四边形.
(2)当 ABCD是菱形时,试判断 AEDF是怎样的特殊平行四边形,并证明你的结论.
(3) AEDF可能是正方形吗 如果可能,指出此时 ABCD是怎样的特殊平行四边形,并证明你的结论;如果不可能,请说明理由.
23.(10分)如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=AD(n为大于2的整数),连接BE,作BE的垂直平分线,分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=a(a为常数),n=3时,求FG的长;
(3)记四边形BFEG的面积为S1,矩形ABCD的面积为S2,当=时,求n的值.(直接写出结果,不必写出解答过程)
24.(12分)倡导研究性学习方式,着力教材研究,习题研究,是学生跳出题海,提高学习能力和创新能力的有效途径.下面是一案例,请同学们认真阅读、研究,完成“类比猜想”及后面的问题.
习题解答:
如图(1),点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.
解:正方形ABCD中,AB=AD,∠BAD=∠ADC=∠B=90°,
把△ABE绕点A逆时针旋转90°至△ADE',如图(1),则点F,D,E'在一条直线上.
∴∠E'AF=90°-45°=45°=∠EAF,
又∵AE'=AE,AF=AF,
∴△AE'F≌△AEF(SAS),
∴EF=E'F=DE'+DF=BE+DF.
习题研究:
观察分析:观察图(1),由解答可知该题有用的条件是:①ABCD是四边形,点E,F分别在边BC,CD上;②AB=AD;③∠B=∠ADC=90°;④∠EAF=∠BAD.
类比猜想:
(1)①在四边形ABCD中,点E,F分别在BC,CD上,当AB=AD,∠B=∠D,∠EAF=∠BAD时,还有EF=BE+DF吗
②研究一个问题,常从特例入手,请同学们研究:如图(2),在菱形ABCD中,点E,F分别在BC,CD上,当∠BAD=120°,∠EAF=60°时,还有EF=BE+DF吗
(2)在四边形ABCD中,点E,F分别在BC,CD上,当AB=AD,∠ABC+∠D=180°,∠EAF=∠BAD时,EF=BE+DF成立吗
归纳概括:
反思前面的解答,思考每个条件的作用,可以得到一个结论为“EF=BE+DF”的一般命题: .
【答案与解析】
1.C(解析:两条直线相交所得的四个角中没有公共边的两个角是对顶角,仅有相等是不够的,故A错误;四个角都相等的四边形只能保证是矩形,故B错误;矩形的对角线仅能保证相等和互相平分,故D错误;而平行四边形的对角线是互相平分的,故C正确.故选C.)
2.C(解析:∵D,E分别是边AB,AC的中点,∴DE是△ABC的中位线.∵DE=2,∴BC=2DE=4.故选C.)
3.C(解析:∵在 ABCD中,AB∥CD,BM是∠ABC的平分线,∴∠CBM=∠ABM=∠CMB,∴MC=BC=2,∵ ABCD的周长是14,∴AB=CD=5,∴DM=3.故选C.)
4.B(解析:根据对角线相等的平行四边形是矩形判定.A选项是邻边相等,可得到平行四边形ABCD是菱形,故不正确;B选项是对角线相等,可推出平行四边形ABCD是矩形,故正确;C选项是对角线互相垂直,可得到平行四边形ABCD是菱形,故不正确;D选项无法判断.故选B.)
5.A(解析:∵菱形ABCD的周长为28,∴AD=7,由题知∠AOD=90°,∵H为AD的中点,∴OH=AD=3.5.)
6.A(解析:如图所示,取AB的中点E,连接OE,DE,OD,则OE=AB=1,AE=1,∴DE=,当D,E,O三点共线时,OD=OE+DE,否则OD7.B(解析:连接BF,如图.在菱形ABCD中,∵∠BAD=80°,∴∠BAF=∠DAF=40°,∵四边形ABCD是菱形,∴AD=AB,又∵AF=AF,∴△BAF≌△DAF,∴BF=DF,∵EF垂直平分AB,∴AF=BF=DF.∴∠ADF=∠DAF=40°.由题意知∠ADC=100°,∴∠CDF=∠ADC-∠ADF=100°-40°=60°.)
8.C(解析:如图,正方形ABCD中,∠BAD=90°,∴∠3=∠BAD=45°.在等边三角形ADE中,∠4=60°,∴∠BAE=∠BAD+∠4=150°.∵AB=AD=AE,∴∠1=∠2=(180°-∠BAE)=15°,∴∠5=∠1+∠3=60°.故选C.)
9.D(解析:根据已知易得∠AEF=180°-∠EFB=120°,∠FEB'=∠EFB=60°,根据翻折变换的性质得∠FEA'=∠AEF=120°,∠A'=∠A=90°,A'E=AE=2,则∠A'EB'=∠FEA'-∠FEB'=120°-60°=60°,从而可知B'E=4,A'B'=2,则AB=A'B'=2,故矩形ABCD的面积=AD·AB=(AE+ED)·AB=(2+6)×2=16.)
10.C(解析:①∵△AEF是等边三角形,∴AE=AF,又∵AB=AD,∴Rt△ABE≌Rt△ADF,∴BE=DF,正确;②∵△ABE≌△ADF,∴∠DAF=∠BAE,又∵∠EAF=60°,∴∠DAF=∠BAE==15°,正确;③∵∠DAF=∠BAE=15°,∠BAC=∠DAC=45°,∴∠EAG=∠FAG=30°,又∵△AEF是等边三角形,∴AC 垂直平分EF,正确;④把△ADF绕点A顺时针旋转90°至△ABF'的位置(或延长EB至F',使BF'=DF,连接AF'),
如图,则∠F'AE=30°,∠F'=∠AEF'=75°,∴EF'≠AE,∵EF'=BE+DF,AE=EF,∴BE+DF≠EF,错误;⑤过点E作EN⊥AF',垂足为N,如图,∵∠NAE=30°,∴NE=AE,∵BE=DF,BC=CD,∴CE=CF,由题意知G为EF中点,∴CG=EF,又∵AE=EF,∴EN=CG,又∵AF'=AE=EF,∴S△AEF'=S△CEF,∴S△CEF=2S△ABE,正确.故选C.)
11.AD=BC(答案不唯一)(解析:本题是一道开放题,灵活利用已有条件AD∥BC,然后再增加另外一组对边平行或AD=BC等,就可以判定是平行四边形,故可填AD=BC.)
12.65(解析:因为∠CEB'=50°,所以∠BEB'=180°-∠CEB'=130°,由矩形ABCD沿AE折叠,可知EA平分∠BEB',即∠AEB'=∠BEB'=65°.)
13.45°(解析:根据正方形与等边三角形的性质,得出∠BAD=90°,∠DAE=∠AED=60°,∴∠BAE=∠BAD+∠DAE=150°,∵AB=AD=AE,∴∠ABE=∠AEB,∴∠AEB=×(180°-∠BAE)=15°,∴∠BED=∠AED-∠AEB=60°-15°=45°.)
14.50°(解析:方法1:如图,延长GF,BC相交于H.∵四边形ABCD是菱形,∴AD∥BC,∠3=∠A=80°,BC=DC.∴∠D=∠FCH.∵E,F分别是BC,DC的中点,∴DF=CF=CE.∴∠1=∠2=50°.又∵∠DFG=∠CFH,∴△DFG≌△CFH.∴∠DGF=∠H,GF=HF.又∵GE⊥AD,AD∥BC,∴GE⊥BC.∴FG=FE=FH.∴∠H=∠1=50°,∴∠DGF=∠H=50°.方法2:∵四边形ABCD为菱形,∴BC=CD,AD∥BC,∠C=∠A=80°.∵EG⊥AD,∴EG⊥BC.∴∠DGF与∠FGE互余,∠CEF与∠FEG互余.
∵E,F分别为BC,CD的中点,∴CE=CF.∴∠CEF=∠CFE=(180°-∠C)=50°.如图,过点F作FH⊥GE于H,则GD∥FH∥BC,从而可知H为EG的中点.可证得△FGH≌△FEH.∴∠FGE=∠FEG.∴∠DGF=∠CEF=50°(等角的余角相等).故填50°.)
15.6(解析:连接BD,DE,如图,∵四边形ABCD是正方形,∴点B与点D关于直线AC对称,∴DE的长即为BQ+QE的最小值,∵DE=BQ+QE===5,∴△BEQ周长的最小值=DE+BE=5+1=6.故填6.)
16.4(解析:两个小正方形周长的和恰好等于大正方形的周长.)
17.(解析:连接BD,AC交于点O,如图.∵四边形ABCD,AGFE是正方形,∴AB=AD,AE=AG,∠DAB=∠EAG=90°,∴∠DAB+∠DAE=∠EAG+∠DAE,∴∠EAB=∠GAD.∴△EAB≌△GAD(SAS).∴EB=GD.∵四边形ABCD是正方形,AB=,∴BD⊥AC,AC=BD=2,∴∠DOG=90°,OA=OD=BD=1.∵AG=1,∴OG=OA+AG=2,∴GD==,∴EB=.故填.)
18.(解析:连接BD,在Rt△ABD中,AB=AD=1,所以BD=.因为A1,D1分别是AB,AD的中点,所以A1D1=BD=.同理,可得A2D2=,A3D3=,A4D4=.所以正方形A1B1C1D1的周长为2,正方形A2B2C2D2的周长为2,正方形A3B3C3D3的周长为,正方形A4B4C4D4的周长为1,从而可知正方形A5B5C5D5的周长为,第六个正方形A6B6C6D6的周长是.)
19.证明:(1)∵四边形ABCD是矩形,∴∠B=∠D=90°,BC=DA,AB=CD,又∵E,F分别是边AB,CD的中点,∴BE=AB,DF=CD,∴BE=DF,∴△BEC≌△DFA. (2)∵四边形ABCD是矩形,∴AE∥CF,AB=CD,又∵E,F分别是边AB,CD的中点,∴AE=AB,CF=CD,∴AE=CF.∴四边形AECF是平行四边形.
20.(1)证明:∵D,E分别是AB,AC的中点,∴DE∥BC,2DE=BC,又∵BE=2DE,EF=BE,∴EF=BC,∵EF∥BC,∴四边形BCFE是平行四边形.又∵BE=EF,∴四边形BCFE是菱形. (2)解:∵∠BCF=120°,∴∠EBC=60°,由(1)知BC=BE,∴△EBC是等边三角形,∵CE=4,∴菱形的边长为4,从而可知高为2,∴菱形的面积为4×2=8.
21.(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°,∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF.在△ABE和△DAF中, ∴△ABE≌△DAF,∴AF=BE.
(2)解:MP与NQ相等.理由如下:如图,过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,从而可知BE=NQ,MP=AF,由(1)知AF=BE,∴MP=NQ.
22.(1)证明:∵AF∥BD,FD∥AC,∴AF∥ED,FD∥AE,∴四边形AEDF是平行四边形. (2)解:当 ABCD是菱形时, AEDF是矩形.证明如下:∵ ABCD是菱形,∴AC⊥BD,∴∠AED=90°,∴ AEDF是矩形. (3)解: AEDF有可能是正方形,此时 ABCD是正方形.证明如下:∵ AEDF是正方形,∴AE=ED,AE⊥ED.∵四边形ABCD是平行四边形,∴AE=EC,BE=ED,∴AC=BD,∴ ABCD是矩形.又∵AE⊥ED,∴ ABCD是正方形.
23.解:(1)四边形BFEG是菱形.理由如下:∵FG为BE的垂直平分线,∴BO=EO,∠BOG=∠EOF=90°,在矩形ABCD中,AD∥BC,∴∠GBO=∠FEO.∴△BOG≌△EOF(ASA).∴BG=EF,∴四边形BFEG是平行四边形.又∵FG⊥BE,∴平行四边形BFEG是菱形. (2)当AB=a,n=3时,AD=2a,DE=a,AE=a,BE= =a,OE=a,设菱形BFEG的边长为x,∵AB2+AF2=BF2,∴a2+=x2,解得x=a,∴OF= =a,∴FG=a. (3)n=6.
24.解:(1)①不一定成立. ②没有EF=BE+DF,而有BE+DF>EF.证明如下:如图(1)所示,作∠BAG=∠DAF,且AG=AF,连接BG,EG,在菱形ABCD中,AB=AD,∴△ABG≌△ADF,∴DF=BG.∵∠BAD=120°,∠EAF=60°,∴∠DAF+∠BAE=∠BAD-∠EAF=120°-60°=60°,∴∠BAG+∠BAE=60°,∴∠GAE=∠FAE.又∵AG=AF,AE=AE,∴△AGE≌△AFE,∴EG=EF.由三角形的三边关系,可知在△BEG中,BE+BG>EG,∴BE+DF>EF. (2)成立.证明如下:如图(2)所示,延长EB至点G,使BG=DF,连接AG.∵∠ABC+∠D=180°,∠ABC+∠ABG=180°,∴∠D=∠ABG.又∵AB=AD,∴△ABG≌△ADF,∴AG=AF,∠BAG=∠DAF.∵∠EAF=∠BAD,∴∠DAF+∠BAE=∠BAD=∠EAF,∴∠BAG+∠BAE=∠BAD,∴∠EAG=∠EAF,∵AE=AE,∴△EAG≌△EAF,∴EG=EF,即EF=BE+BG,∴EF=BE+DF. 在四边形ABCD中,点E,F分别在BC,CD上,当AB=AD,∠B+∠D=180°,∠EAF=∠BAD时,总有EF=BE+DF 成立
21世纪教育网(www.21cnjy.com)
一、选择题(每小题3分,共30分)
1.下列说法中,正确的是 ( )
A.相等的角一定是对顶角
B.四个角都相等的四边形一定是正方形
C.平行四边形的对角线互相平分
D.矩形的对角线一定互相垂直
2.如图,△ABC中,D,E分别是边AB,AC的中点.若DE=2,则BC等于 ( )
A.2 B.3 C.4 D.5
3.如图,在 ABCD中,BM是∠ABC的平分线,交CD于点M,且MC=2, ABCD的周长是14,则DM等于 ( )
A.1 B.2 C.3 D.4
4.在 ABCD中,AC,BD是对角线,如果添加一个条件,即可推出 ABCD是矩形,那么这个条件是 ( )
A.AB=BC B.AC=BD
C.AC⊥BD D.AB⊥BD
5.如图,在菱形ABCD中,对角线AC,BD相交于点O,H为AD的中点,菱形ABCD的周长为28,则OH的长等于 ( )
A.3.5 B.4 C.7 D.14
6.如图所示,∠MON=90°,矩形ABCD的顶点A,B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1.运动过程中,点D到点O的最大距离为( )
A.+1 B. C. D.
7.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于 ( )
A.50° B.60° C.70° D.80°
8.如图,在正方形ABCD的外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为 ( )
A.45° B.55° C.60° D.75°
9.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B'处,点A落在点A'处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是 ( )
A.12 B.24 C.12 D.16
10.如图,正方形 ABCD中,点E,F 分别在 BC,CD上,△AEF是等边三角形,连接AC 交 EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC 垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE .其中正确的结论有 ( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题4分,共32分)
11.如图,在四边形ABCD中,对角线AC,BD交于点O,AD∥BC,请添加一个条件: ,使四边形ABCD为平行四边形(不添加任何辅助线).
12.将矩形ABCD沿AE折叠,得到如图所示的图形.已知∠CEB'=50°,则∠AEB'= °.
13.如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED的度数为 .
14.如图,菱形ABCD中,E,F分别是BC,CD的中点,过点E作EG⊥AD于G,连接EF,GF,若∠A=80°,则∠DGF的度数为 .
15.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为 .
16.如图所示,正方形ABCD中,AB=1,P是对角线AC上的一点,分别以AP,PC为对角线作正方形,则两个小正方形周长的和是 .
17.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=,AG=1,则EB= .
18.如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,又顺次连接正方形A1B1C1D1四边中点得到第二个正方形A2B2C2D2,…,以此类推,则第六个正方形A6B6C6D6的周长是 .
三、解答题(共58分)
19.(8分)如图,在矩形ABCD中,E,F分别是边AB,CD的中点,连接AF,CE.
(1)求证△BEC≌△DFA;
(2)求证四边形AECF是平行四边形.
20.(8分)如图,在△ABC中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
21.(10分)如图(1),在正方形ABCD中,E,F分别是边AD,DC上的点,且AF⊥BE.
(1)求证AF=BE;
(2)如图(2),在正方形ABCD中,M,N,P,Q分别是边AB,BC,CD,DA上的点,且MP⊥NQ.MP与NQ是否相等 并说明理由.
22.(10分)如图,已知 ABCD中,AC与BD相交于点E,AF∥BD,FD∥AC.
(1)求证四边形AEDF是平行四边形.
(2)当 ABCD是菱形时,试判断 AEDF是怎样的特殊平行四边形,并证明你的结论.
(3) AEDF可能是正方形吗 如果可能,指出此时 ABCD是怎样的特殊平行四边形,并证明你的结论;如果不可能,请说明理由.
23.(10分)如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=AD(n为大于2的整数),连接BE,作BE的垂直平分线,分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=a(a为常数),n=3时,求FG的长;
(3)记四边形BFEG的面积为S1,矩形ABCD的面积为S2,当=时,求n的值.(直接写出结果,不必写出解答过程)
24.(12分)倡导研究性学习方式,着力教材研究,习题研究,是学生跳出题海,提高学习能力和创新能力的有效途径.下面是一案例,请同学们认真阅读、研究,完成“类比猜想”及后面的问题.
习题解答:
如图(1),点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.
解:正方形ABCD中,AB=AD,∠BAD=∠ADC=∠B=90°,
把△ABE绕点A逆时针旋转90°至△ADE',如图(1),则点F,D,E'在一条直线上.
∴∠E'AF=90°-45°=45°=∠EAF,
又∵AE'=AE,AF=AF,
∴△AE'F≌△AEF(SAS),
∴EF=E'F=DE'+DF=BE+DF.
习题研究:
观察分析:观察图(1),由解答可知该题有用的条件是:①ABCD是四边形,点E,F分别在边BC,CD上;②AB=AD;③∠B=∠ADC=90°;④∠EAF=∠BAD.
类比猜想:
(1)①在四边形ABCD中,点E,F分别在BC,CD上,当AB=AD,∠B=∠D,∠EAF=∠BAD时,还有EF=BE+DF吗
②研究一个问题,常从特例入手,请同学们研究:如图(2),在菱形ABCD中,点E,F分别在BC,CD上,当∠BAD=120°,∠EAF=60°时,还有EF=BE+DF吗
(2)在四边形ABCD中,点E,F分别在BC,CD上,当AB=AD,∠ABC+∠D=180°,∠EAF=∠BAD时,EF=BE+DF成立吗
归纳概括:
反思前面的解答,思考每个条件的作用,可以得到一个结论为“EF=BE+DF”的一般命题: .
【答案与解析】
1.C(解析:两条直线相交所得的四个角中没有公共边的两个角是对顶角,仅有相等是不够的,故A错误;四个角都相等的四边形只能保证是矩形,故B错误;矩形的对角线仅能保证相等和互相平分,故D错误;而平行四边形的对角线是互相平分的,故C正确.故选C.)
2.C(解析:∵D,E分别是边AB,AC的中点,∴DE是△ABC的中位线.∵DE=2,∴BC=2DE=4.故选C.)
3.C(解析:∵在 ABCD中,AB∥CD,BM是∠ABC的平分线,∴∠CBM=∠ABM=∠CMB,∴MC=BC=2,∵ ABCD的周长是14,∴AB=CD=5,∴DM=3.故选C.)
4.B(解析:根据对角线相等的平行四边形是矩形判定.A选项是邻边相等,可得到平行四边形ABCD是菱形,故不正确;B选项是对角线相等,可推出平行四边形ABCD是矩形,故正确;C选项是对角线互相垂直,可得到平行四边形ABCD是菱形,故不正确;D选项无法判断.故选B.)
5.A(解析:∵菱形ABCD的周长为28,∴AD=7,由题知∠AOD=90°,∵H为AD的中点,∴OH=AD=3.5.)
6.A(解析:如图所示,取AB的中点E,连接OE,DE,OD,则OE=AB=1,AE=1,∴DE=,当D,E,O三点共线时,OD=OE+DE,否则OD
8.C(解析:如图,正方形ABCD中,∠BAD=90°,∴∠3=∠BAD=45°.在等边三角形ADE中,∠4=60°,∴∠BAE=∠BAD+∠4=150°.∵AB=AD=AE,∴∠1=∠2=(180°-∠BAE)=15°,∴∠5=∠1+∠3=60°.故选C.)
9.D(解析:根据已知易得∠AEF=180°-∠EFB=120°,∠FEB'=∠EFB=60°,根据翻折变换的性质得∠FEA'=∠AEF=120°,∠A'=∠A=90°,A'E=AE=2,则∠A'EB'=∠FEA'-∠FEB'=120°-60°=60°,从而可知B'E=4,A'B'=2,则AB=A'B'=2,故矩形ABCD的面积=AD·AB=(AE+ED)·AB=(2+6)×2=16.)
10.C(解析:①∵△AEF是等边三角形,∴AE=AF,又∵AB=AD,∴Rt△ABE≌Rt△ADF,∴BE=DF,正确;②∵△ABE≌△ADF,∴∠DAF=∠BAE,又∵∠EAF=60°,∴∠DAF=∠BAE==15°,正确;③∵∠DAF=∠BAE=15°,∠BAC=∠DAC=45°,∴∠EAG=∠FAG=30°,又∵△AEF是等边三角形,∴AC 垂直平分EF,正确;④把△ADF绕点A顺时针旋转90°至△ABF'的位置(或延长EB至F',使BF'=DF,连接AF'),
如图,则∠F'AE=30°,∠F'=∠AEF'=75°,∴EF'≠AE,∵EF'=BE+DF,AE=EF,∴BE+DF≠EF,错误;⑤过点E作EN⊥AF',垂足为N,如图,∵∠NAE=30°,∴NE=AE,∵BE=DF,BC=CD,∴CE=CF,由题意知G为EF中点,∴CG=EF,又∵AE=EF,∴EN=CG,又∵AF'=AE=EF,∴S△AEF'=S△CEF,∴S△CEF=2S△ABE,正确.故选C.)
11.AD=BC(答案不唯一)(解析:本题是一道开放题,灵活利用已有条件AD∥BC,然后再增加另外一组对边平行或AD=BC等,就可以判定是平行四边形,故可填AD=BC.)
12.65(解析:因为∠CEB'=50°,所以∠BEB'=180°-∠CEB'=130°,由矩形ABCD沿AE折叠,可知EA平分∠BEB',即∠AEB'=∠BEB'=65°.)
13.45°(解析:根据正方形与等边三角形的性质,得出∠BAD=90°,∠DAE=∠AED=60°,∴∠BAE=∠BAD+∠DAE=150°,∵AB=AD=AE,∴∠ABE=∠AEB,∴∠AEB=×(180°-∠BAE)=15°,∴∠BED=∠AED-∠AEB=60°-15°=45°.)
14.50°(解析:方法1:如图,延长GF,BC相交于H.∵四边形ABCD是菱形,∴AD∥BC,∠3=∠A=80°,BC=DC.∴∠D=∠FCH.∵E,F分别是BC,DC的中点,∴DF=CF=CE.∴∠1=∠2=50°.又∵∠DFG=∠CFH,∴△DFG≌△CFH.∴∠DGF=∠H,GF=HF.又∵GE⊥AD,AD∥BC,∴GE⊥BC.∴FG=FE=FH.∴∠H=∠1=50°,∴∠DGF=∠H=50°.方法2:∵四边形ABCD为菱形,∴BC=CD,AD∥BC,∠C=∠A=80°.∵EG⊥AD,∴EG⊥BC.∴∠DGF与∠FGE互余,∠CEF与∠FEG互余.
∵E,F分别为BC,CD的中点,∴CE=CF.∴∠CEF=∠CFE=(180°-∠C)=50°.如图,过点F作FH⊥GE于H,则GD∥FH∥BC,从而可知H为EG的中点.可证得△FGH≌△FEH.∴∠FGE=∠FEG.∴∠DGF=∠CEF=50°(等角的余角相等).故填50°.)
15.6(解析:连接BD,DE,如图,∵四边形ABCD是正方形,∴点B与点D关于直线AC对称,∴DE的长即为BQ+QE的最小值,∵DE=BQ+QE===5,∴△BEQ周长的最小值=DE+BE=5+1=6.故填6.)
16.4(解析:两个小正方形周长的和恰好等于大正方形的周长.)
17.(解析:连接BD,AC交于点O,如图.∵四边形ABCD,AGFE是正方形,∴AB=AD,AE=AG,∠DAB=∠EAG=90°,∴∠DAB+∠DAE=∠EAG+∠DAE,∴∠EAB=∠GAD.∴△EAB≌△GAD(SAS).∴EB=GD.∵四边形ABCD是正方形,AB=,∴BD⊥AC,AC=BD=2,∴∠DOG=90°,OA=OD=BD=1.∵AG=1,∴OG=OA+AG=2,∴GD==,∴EB=.故填.)
18.(解析:连接BD,在Rt△ABD中,AB=AD=1,所以BD=.因为A1,D1分别是AB,AD的中点,所以A1D1=BD=.同理,可得A2D2=,A3D3=,A4D4=.所以正方形A1B1C1D1的周长为2,正方形A2B2C2D2的周长为2,正方形A3B3C3D3的周长为,正方形A4B4C4D4的周长为1,从而可知正方形A5B5C5D5的周长为,第六个正方形A6B6C6D6的周长是.)
19.证明:(1)∵四边形ABCD是矩形,∴∠B=∠D=90°,BC=DA,AB=CD,又∵E,F分别是边AB,CD的中点,∴BE=AB,DF=CD,∴BE=DF,∴△BEC≌△DFA. (2)∵四边形ABCD是矩形,∴AE∥CF,AB=CD,又∵E,F分别是边AB,CD的中点,∴AE=AB,CF=CD,∴AE=CF.∴四边形AECF是平行四边形.
20.(1)证明:∵D,E分别是AB,AC的中点,∴DE∥BC,2DE=BC,又∵BE=2DE,EF=BE,∴EF=BC,∵EF∥BC,∴四边形BCFE是平行四边形.又∵BE=EF,∴四边形BCFE是菱形. (2)解:∵∠BCF=120°,∴∠EBC=60°,由(1)知BC=BE,∴△EBC是等边三角形,∵CE=4,∴菱形的边长为4,从而可知高为2,∴菱形的面积为4×2=8.
21.(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°,∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF.在△ABE和△DAF中, ∴△ABE≌△DAF,∴AF=BE.
(2)解:MP与NQ相等.理由如下:如图,过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,从而可知BE=NQ,MP=AF,由(1)知AF=BE,∴MP=NQ.
22.(1)证明:∵AF∥BD,FD∥AC,∴AF∥ED,FD∥AE,∴四边形AEDF是平行四边形. (2)解:当 ABCD是菱形时, AEDF是矩形.证明如下:∵ ABCD是菱形,∴AC⊥BD,∴∠AED=90°,∴ AEDF是矩形. (3)解: AEDF有可能是正方形,此时 ABCD是正方形.证明如下:∵ AEDF是正方形,∴AE=ED,AE⊥ED.∵四边形ABCD是平行四边形,∴AE=EC,BE=ED,∴AC=BD,∴ ABCD是矩形.又∵AE⊥ED,∴ ABCD是正方形.
23.解:(1)四边形BFEG是菱形.理由如下:∵FG为BE的垂直平分线,∴BO=EO,∠BOG=∠EOF=90°,在矩形ABCD中,AD∥BC,∴∠GBO=∠FEO.∴△BOG≌△EOF(ASA).∴BG=EF,∴四边形BFEG是平行四边形.又∵FG⊥BE,∴平行四边形BFEG是菱形. (2)当AB=a,n=3时,AD=2a,DE=a,AE=a,BE= =a,OE=a,设菱形BFEG的边长为x,∵AB2+AF2=BF2,∴a2+=x2,解得x=a,∴OF= =a,∴FG=a. (3)n=6.
24.解:(1)①不一定成立. ②没有EF=BE+DF,而有BE+DF>EF.证明如下:如图(1)所示,作∠BAG=∠DAF,且AG=AF,连接BG,EG,在菱形ABCD中,AB=AD,∴△ABG≌△ADF,∴DF=BG.∵∠BAD=120°,∠EAF=60°,∴∠DAF+∠BAE=∠BAD-∠EAF=120°-60°=60°,∴∠BAG+∠BAE=60°,∴∠GAE=∠FAE.又∵AG=AF,AE=AE,∴△AGE≌△AFE,∴EG=EF.由三角形的三边关系,可知在△BEG中,BE+BG>EG,∴BE+DF>EF. (2)成立.证明如下:如图(2)所示,延长EB至点G,使BG=DF,连接AG.∵∠ABC+∠D=180°,∠ABC+∠ABG=180°,∴∠D=∠ABG.又∵AB=AD,∴△ABG≌△ADF,∴AG=AF,∠BAG=∠DAF.∵∠EAF=∠BAD,∴∠DAF+∠BAE=∠BAD=∠EAF,∴∠BAG+∠BAE=∠BAD,∴∠EAG=∠EAF,∵AE=AE,∴△EAG≌△EAF,∴EG=EF,即EF=BE+BG,∴EF=BE+DF. 在四边形ABCD中,点E,F分别在BC,CD上,当AB=AD,∠B+∠D=180°,∠EAF=∠BAD时,总有EF=BE+DF 成立
21世纪教育网(www.21cnjy.com)
