2022-2023学年高二数学人教A版(2019)选择性必修第一册教案:1.4.2用空间向量研究距离、夹角问题
文档属性
| 名称 | 2022-2023学年高二数学人教A版(2019)选择性必修第一册教案:1.4.2用空间向量研究距离、夹角问题 |

|
|
| 格式 | doc | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 18:37:23 | ||
图片预览




文档简介
第一章 空间向量与立体几何
1.4 空间向量的应用
1.4.2 用空间向量研究距离、夹角问题
教学设计
一、教学目标
1. 能用向量方法解决点到直线、点到平面、相互平行的直线、相互平行的直线与平面、相互平行的平面的距离问题和简单夹角问题;
2. 能描述解决这一类问题的程序,体会向量方法在研究几何问题中的作用.
二、教学重难点
1. 教学重点
理解并掌握用向量方法解决距离、夹角问题的方法和步骤.
2. 教学难点
辨析各种距离、夹角问题并能正确求出各种距离及夹角.
三、教学过程
(一)新课导入
复习:上节课我们学习了用空间向量研究直线、平面的位置关系,包含哪几部分?
(1)空间中点、直线和平面的向量表示;(2)空间中直线、平面的平行;(3)空间中直线、平面的垂直.
这节课我们继续学习用空间向量研究距离、夹角问题.
(二)探索新知
探究一 用空间向量解决距离问题
问题1 立体几何中的距离问题包括哪些?
(学生自主思考,举手回答,教师总结)
包括点到直线、点到平面、两条平行直线以及两个平行平面的距离向题等.
1. 点到直线的距离
问题2 已知直线l的单位方向向量为u,A是直线l上的定点,P是直线l外一点.如何利用这些条件求点P到直线l的距离?
如图,向量在直线l上的投影向量为,则是直角三角形.因为A,P都是定点,所以与u的夹角都是确定的.于是可求.再利用勾股定理,可以求出点P到直线l的距离PQ.
设,则向量在直线l上的投影向量.
在中,由勾股定理,得.
问题3 类比点到直线的距离的求法,如何求两条平行直线之间的距离?
(学生以小组为单位讨论,每组选出代表回答,教师最后总结)
答:在其中一条直线上取点P,将求两条平行直线之间的距离转化为求点P到另一条直线的距离.
2. 点到平面的距离
如图,已知平面α的法向量为n,A是平面α内的定点,P是平面α外一点.过点P作平面α的垂线l,交平面α于点Q,则n是直线l的方向向量,且点P到平面α的距离就是在直线l上的投影向量的长度.因此.
例1 如图,在棱长为1的正方体中,E为线段的中点,F为线段AB的中点.
(1)求点B到直线的距离;
(2)求直线FC到平面的距离.
解:以为原点,所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则,,,所以,,,.
(1)取,,则.
所以,点B到直线的距离为.
(2)因为,所以,所以平面.所以点F到平面的距离即为直线FC到平面的距离.
设平面的法向量为,则,
所以.
所以.
取,则.所以,是平面的一个法向量.
又因为,所以点F到平面的距离为.
即直线FC到平面的距离为.
用空间向量解决立体几何问题的“三步曲”:
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何向题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
探究二 用空间向量解决夹角问题
1. 异面直线所成的角及直线与平面所成的角
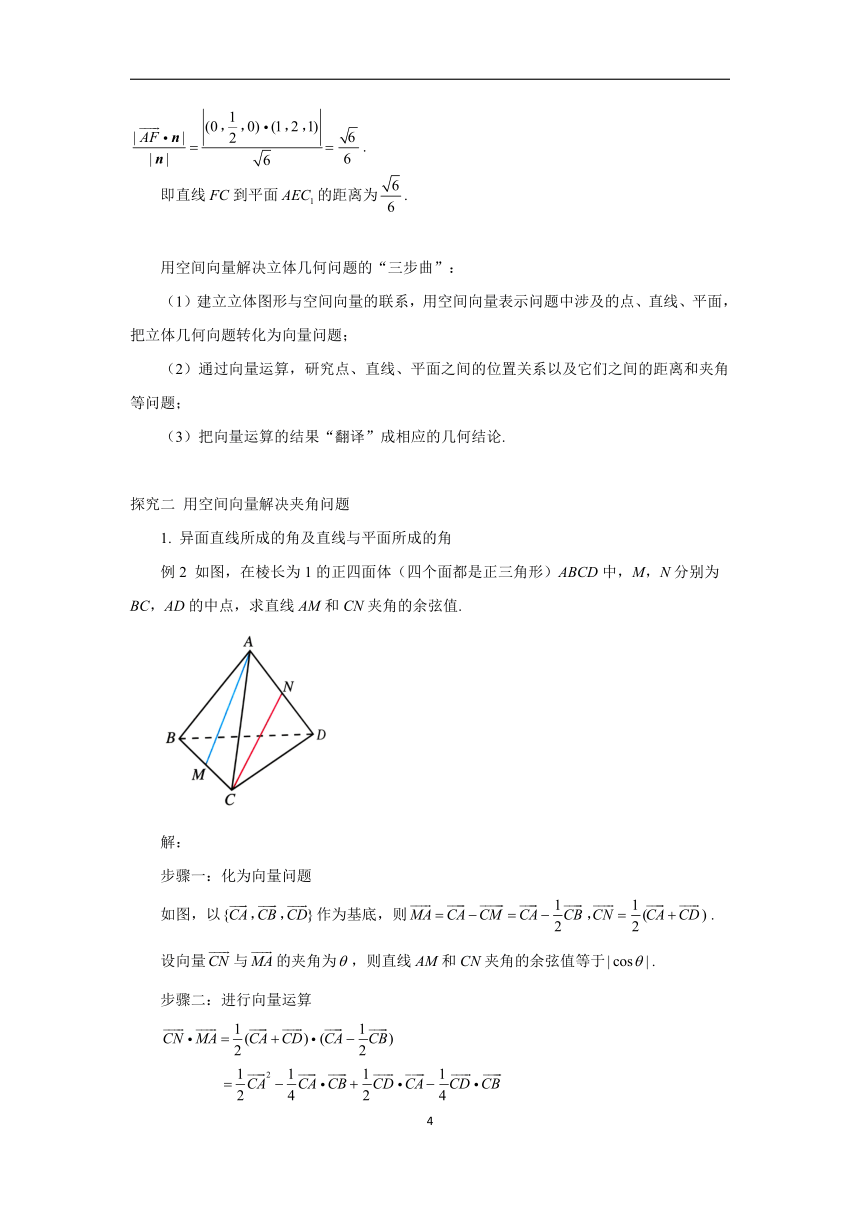
例2 如图,在棱长为1的正四面体(四个面都是正三角形)ABCD中,M,N分别为BC,AD的中点,求直线AM和CN夹角的余弦值.
解:
步骤一:化为向量问题
如图,以作为基底,则.
设向量与的夹角为,则直线AM和CN夹角的余弦值等于.
步骤二:进行向量运算
.
又和均为等边三角形,所以.
所以.
步骤三:回到图形问题
所以直线AM和CN夹角的余弦值为.
一般地,两条异面直线所成的角,可以转化为两条异面直线的方向向量的夹角来求得.也就是说,若异面直线所成的角为,其方向向量分别是u,v,则
.
类似地,直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.如下图,直线AB与平面α相交于点B,设直线AB与平面α所成的角为,直线AB的方向向量为u,平面α的法向量为n,则
.
2. 两平面的夹角
如下图,平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于的二面角称为平面α与平面β的夹角.
类似于两条异面直线所成的角,若平面α,β的法向量分别是和,则平面α与平面β的夹角即为向量和的夹角或其补角.设平面α与平面β的夹角为,则
.
例3 如图,在直三棱柱中,,P为BC的中点,点Q,R分别在棱上,.求平面PQR与平面夹角的余弦值.
解:
步骤一:化为向量问题
以为原点,所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系.设平面的法向量为,平面PQR的法向量为,则平面PQR与平面的夹角就是与的夹角或其补角.
步骤二:进行向量运算
因为平面,所以平面的一个法向量为.
根据所建立的空间直角坐标系,可知.
所以.设,
则,所以,所以.
取,则.
步骤三:回到图形问题
设平面PQR与平面的夹角为,则.
即平面PQR与平面的夹角的余弦值为.
探究三 用空间向量解决实际问题及综合应用
例4 下图为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为30°.已知礼物的质量为1 kg,每根绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度g取9.8 m/s ,精确到0.01 N).
解:如图,设水平面的单位法向量为n,其中每一根绳子的拉力均为F.
因为,所以F在n上的投影向量为.
所以8根绳子拉力的合力.
又因为降落伞匀速下落,所以.
所以.
所以.
例5 如图,在四棱锥中,底面ABCD是正方形,侧棱底面ABCD,,E是PC的中点,作交PB于点F.
(1)求证:平面EDB;
(2)求证:平面EFD;
(3)求平面CPB与平面PBD的夹角的大小.
解:以D为原点,DA,DC,DP所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.设.
(1)连接AC,交BD于点G,连接EG.
依题意得.
因为底面ABCD是正方形,所以点G是它的中心,故点G的坐标为,且.
所以,即.
而平面EDB,且平面EDB,因此平面EDB.
(2)证明:依题意得.
又,故.
所以.
由已知,且,所以平面EFD.
(3)解:已知,由(2)可知,故是平面CPB与平面PBD的夹角.
设点F的坐标为,则.
因为,所以,即.
设,则.
所以,点F的坐标为.
又点E的坐标为,所以.
所以.
所以,即平面CPB与平面PBD的夹角大小为60°.
探究四 解决立体几何问题的方法
解决立体几何中的问题,可用三种方法:
(1)综合法:以逻辑推理作为工具解决问题;
(2)向量法:利用向量的概念及其运算解决问题;
(3)坐标法:利用数及其运算来解决问题.
(三)课堂练习
1.已知平面的一个法向量,点在平面内,则点到平面的距离为( )
A.10 B.3 C. D.
答案:D
解析:由,得点到平面的距离.
2.如图所示,在三棱柱中,底面,点分别是棱的中点,则直线和的夹角是( )
A. B. C. D.
答案:C
解析:如图所示,建立空间直角坐标系,
由于,不妨取,则,
,
,
所以异面直线和的夹角为,故选C.
3.如图,在空间直角坐标系中,四棱柱为长方体,,点为的中点,则平面与平面夹角的余弦值为( )
A. B. C. D.
答案:C
解析:设,则,因为分别为,的中点,所以,所以,设是平面的法向量,则,所以,所以,取,则,所以平面的一个法向量为.又平面,所以是平面的一个法向量,因为,所以平面与平面夹角的余弦值为,故选C.
4.如图,在长方体中,,点分别是的中点,则点到直线的距离为_________.
答案:
解析:以为坐标原点,所在的直线分别为轴,轴,轴建立如图所示的空间直角坐标系,
则,于是有,所以,,所以点到直线的距离为.
5.在平行六面体中,以顶点为端点的三条棱两两夹角都为,且分别为的中点,则与所成角的余弦值为_________.
答案:
解析:连接,易知即与所成的角,设,则由条件,知,,,,因为,所以,,
又,故.
(四)小结作业
小结:用向量方法解决点到直线、点到平面、相互平行的直线、相互平行的直线与平面、相互平行的平面的距离问题和简单夹角问题.
作业:
四、板书设计
1.4.2 用空间向量研究距离、夹角问题
1. 用空间向量解决距离问题:
(1)点到直线的距离;
(2)点到平面的距离.
2. 用空间向量解决夹角问题:
(1)异面直线所成的角及直线与平面所成的角;
(2)两平面的夹角
3. 用空间向量解决实际问题及综合应用
4. 解决立体几何问题的方法
2
1.4 空间向量的应用
1.4.2 用空间向量研究距离、夹角问题
教学设计
一、教学目标
1. 能用向量方法解决点到直线、点到平面、相互平行的直线、相互平行的直线与平面、相互平行的平面的距离问题和简单夹角问题;
2. 能描述解决这一类问题的程序,体会向量方法在研究几何问题中的作用.
二、教学重难点
1. 教学重点
理解并掌握用向量方法解决距离、夹角问题的方法和步骤.
2. 教学难点
辨析各种距离、夹角问题并能正确求出各种距离及夹角.
三、教学过程
(一)新课导入
复习:上节课我们学习了用空间向量研究直线、平面的位置关系,包含哪几部分?
(1)空间中点、直线和平面的向量表示;(2)空间中直线、平面的平行;(3)空间中直线、平面的垂直.
这节课我们继续学习用空间向量研究距离、夹角问题.
(二)探索新知
探究一 用空间向量解决距离问题
问题1 立体几何中的距离问题包括哪些?
(学生自主思考,举手回答,教师总结)
包括点到直线、点到平面、两条平行直线以及两个平行平面的距离向题等.
1. 点到直线的距离
问题2 已知直线l的单位方向向量为u,A是直线l上的定点,P是直线l外一点.如何利用这些条件求点P到直线l的距离?
如图,向量在直线l上的投影向量为,则是直角三角形.因为A,P都是定点,所以与u的夹角都是确定的.于是可求.再利用勾股定理,可以求出点P到直线l的距离PQ.
设,则向量在直线l上的投影向量.
在中,由勾股定理,得.
问题3 类比点到直线的距离的求法,如何求两条平行直线之间的距离?
(学生以小组为单位讨论,每组选出代表回答,教师最后总结)
答:在其中一条直线上取点P,将求两条平行直线之间的距离转化为求点P到另一条直线的距离.
2. 点到平面的距离
如图,已知平面α的法向量为n,A是平面α内的定点,P是平面α外一点.过点P作平面α的垂线l,交平面α于点Q,则n是直线l的方向向量,且点P到平面α的距离就是在直线l上的投影向量的长度.因此.
例1 如图,在棱长为1的正方体中,E为线段的中点,F为线段AB的中点.
(1)求点B到直线的距离;
(2)求直线FC到平面的距离.
解:以为原点,所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则,,,所以,,,.
(1)取,,则.
所以,点B到直线的距离为.
(2)因为,所以,所以平面.所以点F到平面的距离即为直线FC到平面的距离.
设平面的法向量为,则,
所以.
所以.
取,则.所以,是平面的一个法向量.
又因为,所以点F到平面的距离为.
即直线FC到平面的距离为.
用空间向量解决立体几何问题的“三步曲”:
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何向题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
探究二 用空间向量解决夹角问题
1. 异面直线所成的角及直线与平面所成的角
例2 如图,在棱长为1的正四面体(四个面都是正三角形)ABCD中,M,N分别为BC,AD的中点,求直线AM和CN夹角的余弦值.
解:
步骤一:化为向量问题
如图,以作为基底,则.
设向量与的夹角为,则直线AM和CN夹角的余弦值等于.
步骤二:进行向量运算
.
又和均为等边三角形,所以.
所以.
步骤三:回到图形问题
所以直线AM和CN夹角的余弦值为.
一般地,两条异面直线所成的角,可以转化为两条异面直线的方向向量的夹角来求得.也就是说,若异面直线所成的角为,其方向向量分别是u,v,则
.
类似地,直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.如下图,直线AB与平面α相交于点B,设直线AB与平面α所成的角为,直线AB的方向向量为u,平面α的法向量为n,则
.
2. 两平面的夹角
如下图,平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于的二面角称为平面α与平面β的夹角.
类似于两条异面直线所成的角,若平面α,β的法向量分别是和,则平面α与平面β的夹角即为向量和的夹角或其补角.设平面α与平面β的夹角为,则
.
例3 如图,在直三棱柱中,,P为BC的中点,点Q,R分别在棱上,.求平面PQR与平面夹角的余弦值.
解:
步骤一:化为向量问题
以为原点,所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系.设平面的法向量为,平面PQR的法向量为,则平面PQR与平面的夹角就是与的夹角或其补角.
步骤二:进行向量运算
因为平面,所以平面的一个法向量为.
根据所建立的空间直角坐标系,可知.
所以.设,
则,所以,所以.
取,则.
步骤三:回到图形问题
设平面PQR与平面的夹角为,则.
即平面PQR与平面的夹角的余弦值为.
探究三 用空间向量解决实际问题及综合应用
例4 下图为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为30°.已知礼物的质量为1 kg,每根绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度g取9.8 m/s ,精确到0.01 N).
解:如图,设水平面的单位法向量为n,其中每一根绳子的拉力均为F.
因为,所以F在n上的投影向量为.
所以8根绳子拉力的合力.
又因为降落伞匀速下落,所以.
所以.
所以.
例5 如图,在四棱锥中,底面ABCD是正方形,侧棱底面ABCD,,E是PC的中点,作交PB于点F.
(1)求证:平面EDB;
(2)求证:平面EFD;
(3)求平面CPB与平面PBD的夹角的大小.
解:以D为原点,DA,DC,DP所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.设.
(1)连接AC,交BD于点G,连接EG.
依题意得.
因为底面ABCD是正方形,所以点G是它的中心,故点G的坐标为,且.
所以,即.
而平面EDB,且平面EDB,因此平面EDB.
(2)证明:依题意得.
又,故.
所以.
由已知,且,所以平面EFD.
(3)解:已知,由(2)可知,故是平面CPB与平面PBD的夹角.
设点F的坐标为,则.
因为,所以,即.
设,则.
所以,点F的坐标为.
又点E的坐标为,所以.
所以.
所以,即平面CPB与平面PBD的夹角大小为60°.
探究四 解决立体几何问题的方法
解决立体几何中的问题,可用三种方法:
(1)综合法:以逻辑推理作为工具解决问题;
(2)向量法:利用向量的概念及其运算解决问题;
(3)坐标法:利用数及其运算来解决问题.
(三)课堂练习
1.已知平面的一个法向量,点在平面内,则点到平面的距离为( )
A.10 B.3 C. D.
答案:D
解析:由,得点到平面的距离.
2.如图所示,在三棱柱中,底面,点分别是棱的中点,则直线和的夹角是( )
A. B. C. D.
答案:C
解析:如图所示,建立空间直角坐标系,
由于,不妨取,则,
,
,
所以异面直线和的夹角为,故选C.
3.如图,在空间直角坐标系中,四棱柱为长方体,,点为的中点,则平面与平面夹角的余弦值为( )
A. B. C. D.
答案:C
解析:设,则,因为分别为,的中点,所以,所以,设是平面的法向量,则,所以,所以,取,则,所以平面的一个法向量为.又平面,所以是平面的一个法向量,因为,所以平面与平面夹角的余弦值为,故选C.
4.如图,在长方体中,,点分别是的中点,则点到直线的距离为_________.
答案:
解析:以为坐标原点,所在的直线分别为轴,轴,轴建立如图所示的空间直角坐标系,
则,于是有,所以,,所以点到直线的距离为.
5.在平行六面体中,以顶点为端点的三条棱两两夹角都为,且分别为的中点,则与所成角的余弦值为_________.
答案:
解析:连接,易知即与所成的角,设,则由条件,知,,,,因为,所以,,
又,故.
(四)小结作业
小结:用向量方法解决点到直线、点到平面、相互平行的直线、相互平行的直线与平面、相互平行的平面的距离问题和简单夹角问题.
作业:
四、板书设计
1.4.2 用空间向量研究距离、夹角问题
1. 用空间向量解决距离问题:
(1)点到直线的距离;
(2)点到平面的距离.
2. 用空间向量解决夹角问题:
(1)异面直线所成的角及直线与平面所成的角;
(2)两平面的夹角
3. 用空间向量解决实际问题及综合应用
4. 解决立体几何问题的方法
2
