全等三角形条件(第一课时)[上学期]
文档属性
| 名称 | 全等三角形条件(第一课时)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 83.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-06 13:49:00 | ||
图片预览

文档简介
13.2 三角形全等的条件(第1课时)
【教学任务分析】
教学目标 知识技能 理解三边对应相等的两个三角形全等的内容.2.初步运用“边边边”条件证明两个三角形全等.
数学思考 使学生经历探索三角形全等的全过程,体验用操作,分类,归纳得出数学结论的过程.
解决问题 会运用“边边边”条件证明两个三角形全等.
情感态度 通过探索三角形全等的条件的活动,培养学生的合作交流的意识和发现问题的能力.2.通过分类,操作等活动培养学生乐于探究的良好品质.
重点 探究三角形全等的方法及运用“边边边”条件证明两个三角形全等.
难点 探究三角形全等的条件.
【教学过程设计】
问题与情景 师生行为 设计意图
活动1问题(1)学校有两块三角形装饰板如下图,小明想知道这两块板是否全等,这两块板很重又固定在墙上,小明只有刻度尺,你能帮小明想个办法吗?(2)三条边对应相等,三个角对应相等两个三角形全等,有没有更简单的办法呢 教师提出问题(1),引导学生思考,回答.教师提出问题(2),学生讨论并回答,教师板书课题.本次活动中教师应重点关注:(1)学生能否大胆的猜想;(2)学生是否积极的参与讨论;(3)学生能否明确两个三角形满足六个条件就能保证三角形全等;(4)学生是否有探究两个三角形全等所需条件的欲望. 通过实际问题为切入点,激发学生的好奇心和探究的欲望,引导学生主动参与数学活动,感知数学与生活密切相关.明确探究方向,培养学生勇于发现,敢于表达的探究意识.
问题与情景 师生行为 设计意图
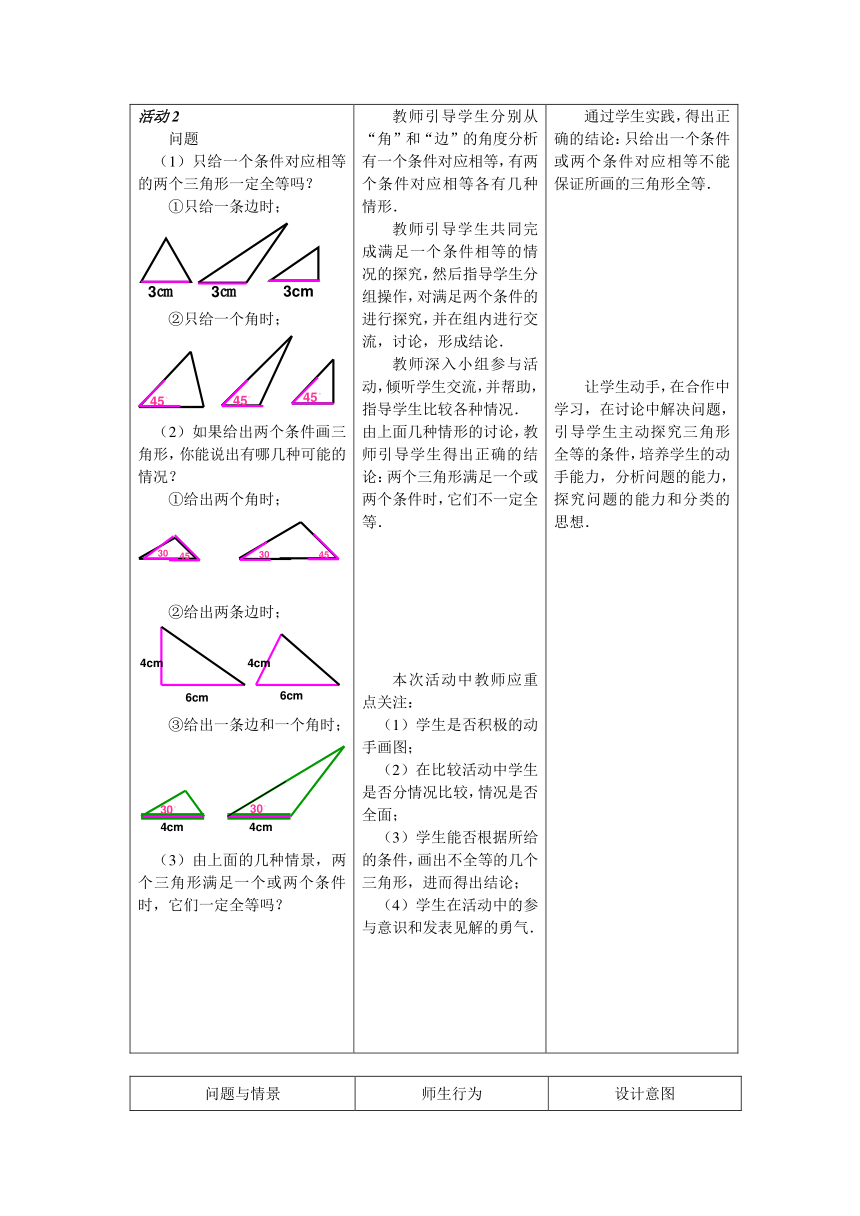
活动2问题(1)只给一个条件对应相等的两个三角形一定全等吗?①只给一条边时;②只给一个角时;(2)如果给出两个条件画三角形,你能说出有哪几种可能的情况?①给出两个角时;②给出两条边时;③给出一条边和一个角时;(3)由上面的几种情景,两个三角形满足一个或两个条件时,它们一定全等吗? 教师引导学生分别从“角”和“边”的角度分析有一个条件对应相等,有两个条件对应相等各有几种情形.教师引导学生共同完成满足一个条件相等的情况的探究,然后指导学生分组操作,对满足两个条件的进行探究,并在组内进行交流,讨论,形成结论.教师深入小组参与活动,倾听学生交流,并帮助,指导学生比较各种情况.由上面几种情形的讨论,教师引导学生得出正确的结论:两个三角形满足一个或两个条件时,它们不一定全等.本次活动中教师应重点关注:(1)学生是否积极的动手画图;(2)在比较活动中学生是否分情况比较,情况是否全面;(3)学生能否根据所给的条件,画出不全等的几个三角形,进而得出结论;(4)学生在活动中的参与意识和发表见解的勇气. 通过学生实践,得出正确的结论:只给出一个条件或两个条件对应相等不能保证所画的三角形全等.让学生动手,在合作中学习,在讨论中解决问题,引导学生主动探究三角形全等的条件,培养学生的动手能力,分析问题的能力,探究问题的能力和分类的思想.
问题与情景 师生行为 设计意图
活动3问题(1)如果两个三角形有三个条件对应相等,这两个三角形全等吗?我们也可以分情况讨论,有哪几种情况?①我们先来探究两个三角形三个角相等的情况:②画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?(2)上面的探究反映了什么规律? 教师先提出问题,引导学生回答出满足三个条件的四种情况,教师再明确探究的任务,指导学生画图探究,获取“SSS”的条件.在画图中,教师可让学生试着画图,在让学生发现存在的问题,最后给出正确的画法.本次活动中教师应重点关注:(1)学生能否根据条件正确的画出图形;(2)学生能否根据探究中发现的规律概括出结论“SSS”;(3)在阐述结论时,学生的语言是否规范;(4)学生是否掌握“SSS”的书写格式. 让学生明确满足条件中的三个有哪几种情形,为以后的学习埋下伏笔. 以学生的画图活动为主线开展探究活动,注重“SSS”条件的发生过程和学生的亲身体验,从实践中获取“SSS”的条件,培养学生探索,发现,概括规律的能力.
活动4问题三角形的三边长度固定,这个三角形的形状大小就完全确定,你能解释其中的道理吗? 你能说出生活中看到的例子吗 教师先提出问题,引导学生正确的回答问题.教师指出:三角形的三边长度固定,这个三角形的形状大小就完全确定,这个性质叫三角形的稳定性.让学生举出生活中的实例.本次活动中教师应重点关注:(1)学生对“SSS”的理解;(2)学生能否发现生活中三角形稳定性的实例;(3)学生是否积极的思考问题. 通过生活中的实例,让学生充分体验当三角形的三边确定后,三角形就唯一确定,加深对“SSS”的理解,使学生找到生活与数学之间的联系.
问题与情景 师生行为 设计意图
活动5问题例1.如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证: △ABD≌△ACD练习题:如图,AB=AD,BC=CD,求证:(1)△ABC≌△ADC(2)∠B=∠D 思考题:如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 教师引导学生分析问题中的已知条件,以及两个三角形全等还需要的条件.学生先独立思考,然后分析,讨论,小组间交流,教师板书过程.本次活动中教师应重点关注:(1)学生能否找到已知条件和隐含的条件;(2)学生能否掌握解题的过程.练习题学生独立分析,写出证明过程,教师点评.练习中教师应重点关注:(1)学生对新知识的掌握程度;(2)学生的证明过程是否规范.在独立思考的基础上,教师引导学生观察图形,寻找隐含条件,教师强调:已知条件包括两个部分,一是直接给出的,一是图形中隐含的. 通过例题的讲解,引导学生分析,解题,培养学生的逻辑推理能力,学会运用“SSS”条件判断三角形全等.通过练习,学生的板书,及时的发现存在的问题,培养的独立分析能力,会运用“SSS”条件判定三角形全等,规范学生的解题过程.通过学生的独立思考,培养学生观察问题的能力和分析问题德能力,会从问题的条件出发,获得运用“SSS”条件所需要的条件.
活动6小结从本节课的学习中你有何收获?布置作业教科书103页习题13.2第1题,第2题. 学生自我小结,相互补充,教师点评.本次活动中教师应重点关注:(1)不同层次的学生对知识的理解程度,有针对性地给予指导;(2)对学生在练习中存在的问题,有针对性地讲解. 通过小结,引导学生学会反思,通过独立思考,引导学生学会自我评价.通过学生练习,及时地了解学习效果,调整教学安排.
3cm
3㎝
3㎝
45
45
45
30
45
30
45
4cm
4cm
6cm
6cm
30
30
4cm
4cm
800
700
300
800
700
300
D
B
C
A
D
C
B
A
D
C
B
A
【教学任务分析】
教学目标 知识技能 理解三边对应相等的两个三角形全等的内容.2.初步运用“边边边”条件证明两个三角形全等.
数学思考 使学生经历探索三角形全等的全过程,体验用操作,分类,归纳得出数学结论的过程.
解决问题 会运用“边边边”条件证明两个三角形全等.
情感态度 通过探索三角形全等的条件的活动,培养学生的合作交流的意识和发现问题的能力.2.通过分类,操作等活动培养学生乐于探究的良好品质.
重点 探究三角形全等的方法及运用“边边边”条件证明两个三角形全等.
难点 探究三角形全等的条件.
【教学过程设计】
问题与情景 师生行为 设计意图
活动1问题(1)学校有两块三角形装饰板如下图,小明想知道这两块板是否全等,这两块板很重又固定在墙上,小明只有刻度尺,你能帮小明想个办法吗?(2)三条边对应相等,三个角对应相等两个三角形全等,有没有更简单的办法呢 教师提出问题(1),引导学生思考,回答.教师提出问题(2),学生讨论并回答,教师板书课题.本次活动中教师应重点关注:(1)学生能否大胆的猜想;(2)学生是否积极的参与讨论;(3)学生能否明确两个三角形满足六个条件就能保证三角形全等;(4)学生是否有探究两个三角形全等所需条件的欲望. 通过实际问题为切入点,激发学生的好奇心和探究的欲望,引导学生主动参与数学活动,感知数学与生活密切相关.明确探究方向,培养学生勇于发现,敢于表达的探究意识.
问题与情景 师生行为 设计意图
活动2问题(1)只给一个条件对应相等的两个三角形一定全等吗?①只给一条边时;②只给一个角时;(2)如果给出两个条件画三角形,你能说出有哪几种可能的情况?①给出两个角时;②给出两条边时;③给出一条边和一个角时;(3)由上面的几种情景,两个三角形满足一个或两个条件时,它们一定全等吗? 教师引导学生分别从“角”和“边”的角度分析有一个条件对应相等,有两个条件对应相等各有几种情形.教师引导学生共同完成满足一个条件相等的情况的探究,然后指导学生分组操作,对满足两个条件的进行探究,并在组内进行交流,讨论,形成结论.教师深入小组参与活动,倾听学生交流,并帮助,指导学生比较各种情况.由上面几种情形的讨论,教师引导学生得出正确的结论:两个三角形满足一个或两个条件时,它们不一定全等.本次活动中教师应重点关注:(1)学生是否积极的动手画图;(2)在比较活动中学生是否分情况比较,情况是否全面;(3)学生能否根据所给的条件,画出不全等的几个三角形,进而得出结论;(4)学生在活动中的参与意识和发表见解的勇气. 通过学生实践,得出正确的结论:只给出一个条件或两个条件对应相等不能保证所画的三角形全等.让学生动手,在合作中学习,在讨论中解决问题,引导学生主动探究三角形全等的条件,培养学生的动手能力,分析问题的能力,探究问题的能力和分类的思想.
问题与情景 师生行为 设计意图
活动3问题(1)如果两个三角形有三个条件对应相等,这两个三角形全等吗?我们也可以分情况讨论,有哪几种情况?①我们先来探究两个三角形三个角相等的情况:②画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?(2)上面的探究反映了什么规律? 教师先提出问题,引导学生回答出满足三个条件的四种情况,教师再明确探究的任务,指导学生画图探究,获取“SSS”的条件.在画图中,教师可让学生试着画图,在让学生发现存在的问题,最后给出正确的画法.本次活动中教师应重点关注:(1)学生能否根据条件正确的画出图形;(2)学生能否根据探究中发现的规律概括出结论“SSS”;(3)在阐述结论时,学生的语言是否规范;(4)学生是否掌握“SSS”的书写格式. 让学生明确满足条件中的三个有哪几种情形,为以后的学习埋下伏笔. 以学生的画图活动为主线开展探究活动,注重“SSS”条件的发生过程和学生的亲身体验,从实践中获取“SSS”的条件,培养学生探索,发现,概括规律的能力.
活动4问题三角形的三边长度固定,这个三角形的形状大小就完全确定,你能解释其中的道理吗? 你能说出生活中看到的例子吗 教师先提出问题,引导学生正确的回答问题.教师指出:三角形的三边长度固定,这个三角形的形状大小就完全确定,这个性质叫三角形的稳定性.让学生举出生活中的实例.本次活动中教师应重点关注:(1)学生对“SSS”的理解;(2)学生能否发现生活中三角形稳定性的实例;(3)学生是否积极的思考问题. 通过生活中的实例,让学生充分体验当三角形的三边确定后,三角形就唯一确定,加深对“SSS”的理解,使学生找到生活与数学之间的联系.
问题与情景 师生行为 设计意图
活动5问题例1.如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证: △ABD≌△ACD练习题:如图,AB=AD,BC=CD,求证:(1)△ABC≌△ADC(2)∠B=∠D 思考题:如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 教师引导学生分析问题中的已知条件,以及两个三角形全等还需要的条件.学生先独立思考,然后分析,讨论,小组间交流,教师板书过程.本次活动中教师应重点关注:(1)学生能否找到已知条件和隐含的条件;(2)学生能否掌握解题的过程.练习题学生独立分析,写出证明过程,教师点评.练习中教师应重点关注:(1)学生对新知识的掌握程度;(2)学生的证明过程是否规范.在独立思考的基础上,教师引导学生观察图形,寻找隐含条件,教师强调:已知条件包括两个部分,一是直接给出的,一是图形中隐含的. 通过例题的讲解,引导学生分析,解题,培养学生的逻辑推理能力,学会运用“SSS”条件判断三角形全等.通过练习,学生的板书,及时的发现存在的问题,培养的独立分析能力,会运用“SSS”条件判定三角形全等,规范学生的解题过程.通过学生的独立思考,培养学生观察问题的能力和分析问题德能力,会从问题的条件出发,获得运用“SSS”条件所需要的条件.
活动6小结从本节课的学习中你有何收获?布置作业教科书103页习题13.2第1题,第2题. 学生自我小结,相互补充,教师点评.本次活动中教师应重点关注:(1)不同层次的学生对知识的理解程度,有针对性地给予指导;(2)对学生在练习中存在的问题,有针对性地讲解. 通过小结,引导学生学会反思,通过独立思考,引导学生学会自我评价.通过学生练习,及时地了解学习效果,调整教学安排.
3cm
3㎝
3㎝
45
45
45
30
45
30
45
4cm
4cm
6cm
6cm
30
30
4cm
4cm
800
700
300
800
700
300
D
B
C
A
D
C
B
A
D
C
B
A
