13.2全等三角形的条件(2)[上学期]
文档属性
| 名称 | 13.2全等三角形的条件(2)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 274.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-14 11:09:00 | ||
图片预览



文档简介
课件11张PPT。1.5三角形全等的条件(2)学习目标
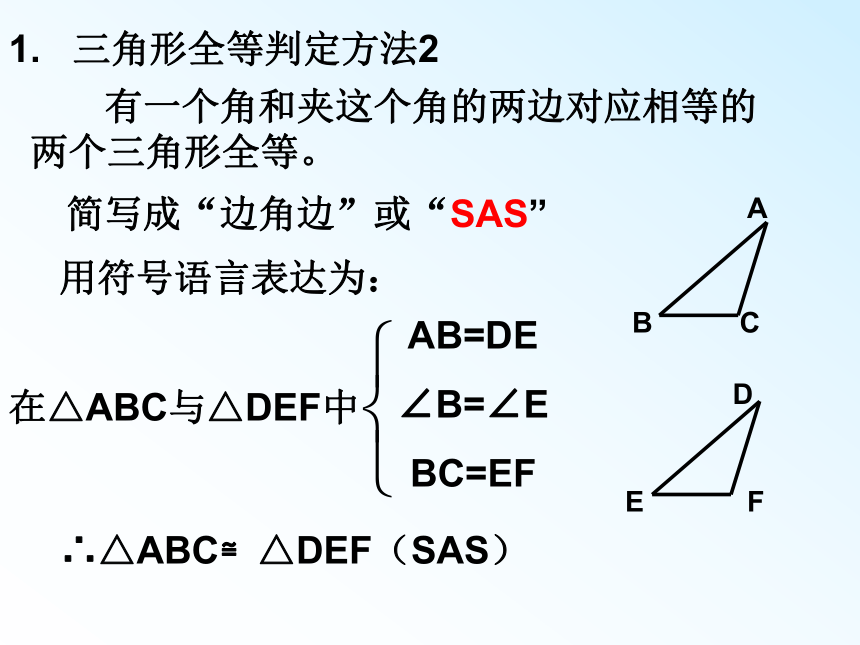
掌握三角形全等的“边角边”公里 ,能够进行有条理的思考并进行简单的推理。做一做:画△ABC,使AB=3cm,AC=4cm。画法:2. 在射线AM上截取AB= 3cm3. 在射线AN上截取AC=4cm提问: 上节课我们学习了判断两个三角形全等的条件是什么?(三个条件) 这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗?若再加一个条件,使∠A=45°,画出△ABC1. 画∠MAN= 45°4.连接BC∴△ABC就是所求的三角形把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?1. 三角形全等判定方法2用符号语言表达为:在△ABC与△DEF中AB=DE
∠B=∠E
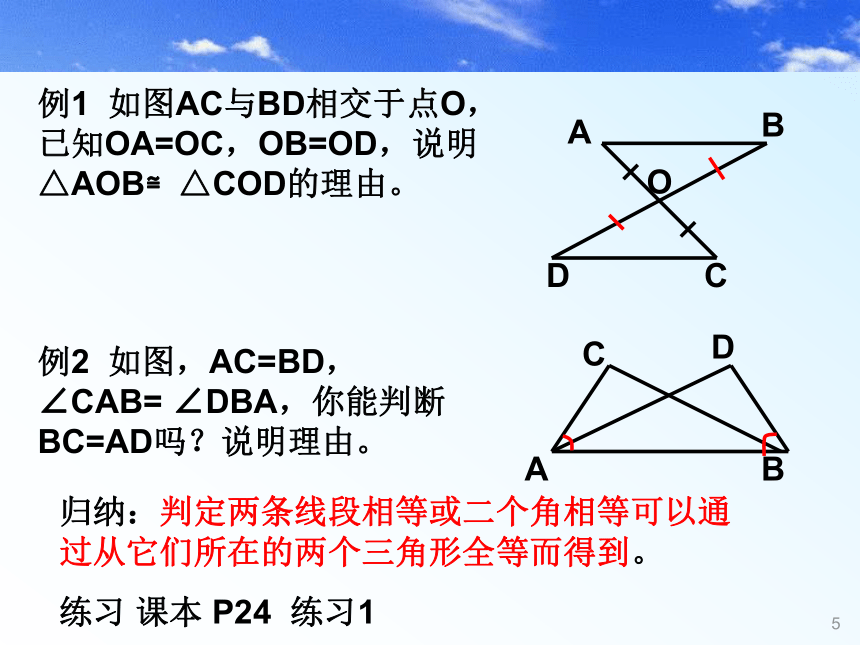
BC=EF∴△ABC≌△DEF(SAS) 有一个角和夹这个角的两边对应相等的两个三角形全等。简写成“边角边”或“SAS”例1 如图AC与BD相交于点O,已知OA=OC,OB=OD,说明△AOB≌△COD的理由。例2 如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?说明理由。归纳:判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到。练习 课本 P24 练习1猜一猜:是不是二条边和一个角对应相等,这样的两个三角形一定全等吗?你能举例说明吗?如图△ABC与△ABD中,AB=AB,AC=BD, ∠B=∠B他们全等吗?注:这个角一定要是这两边所夹的角OA=OB
∠COA=∠COB
OC=OCB解:已知OA=OB,当点C与点O重合时,显然CA=CB,当点C与点O不重合时,∴∠COA=∠BOC=90°在△COA与△COB中∴△COA≌△COB( SAS)∴CA=CB(全等三角形对应边相等)垂直平分线的定义:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线。垂直平分线的性质:线段的垂直平分线上的点到线段两端点的距离相等。式子表达为∴CA=CB补充练习:①. 如图(1), △ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.课堂小结:2. 用尺规作图,已知一角与夹角两边的三角形3. 线段垂直平分线的概念1. 三角形全等的判定方法二,有一个角和夹这个角的两边也对应相等的两个三角形全等(边角边或SAS)4. 线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等.作业:
阅读课本
作业本
同步练习
掌握三角形全等的“边角边”公里 ,能够进行有条理的思考并进行简单的推理。做一做:画△ABC,使AB=3cm,AC=4cm。画法:2. 在射线AM上截取AB= 3cm3. 在射线AN上截取AC=4cm提问: 上节课我们学习了判断两个三角形全等的条件是什么?(三个条件) 这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗?若再加一个条件,使∠A=45°,画出△ABC1. 画∠MAN= 45°4.连接BC∴△ABC就是所求的三角形把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?1. 三角形全等判定方法2用符号语言表达为:在△ABC与△DEF中AB=DE
∠B=∠E
BC=EF∴△ABC≌△DEF(SAS) 有一个角和夹这个角的两边对应相等的两个三角形全等。简写成“边角边”或“SAS”例1 如图AC与BD相交于点O,已知OA=OC,OB=OD,说明△AOB≌△COD的理由。例2 如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?说明理由。归纳:判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到。练习 课本 P24 练习1猜一猜:是不是二条边和一个角对应相等,这样的两个三角形一定全等吗?你能举例说明吗?如图△ABC与△ABD中,AB=AB,AC=BD, ∠B=∠B他们全等吗?注:这个角一定要是这两边所夹的角OA=OB
∠COA=∠COB
OC=OCB解:已知OA=OB,当点C与点O重合时,显然CA=CB,当点C与点O不重合时,∴∠COA=∠BOC=90°在△COA与△COB中∴△COA≌△COB( SAS)∴CA=CB(全等三角形对应边相等)垂直平分线的定义:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线。垂直平分线的性质:线段的垂直平分线上的点到线段两端点的距离相等。式子表达为∴CA=CB补充练习:①. 如图(1), △ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.课堂小结:2. 用尺规作图,已知一角与夹角两边的三角形3. 线段垂直平分线的概念1. 三角形全等的判定方法二,有一个角和夹这个角的两边也对应相等的两个三角形全等(边角边或SAS)4. 线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等.作业:
阅读课本
作业本
同步练习
