13.2.4全等三角形复习[上学期]
文档属性
| 名称 | 13.2.4全等三角形复习[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 153.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-20 22:45:00 | ||
图片预览


文档简介
课件10张PPT。全等三角形复习 1.什么样的图形是全等三角形?2.判定两个三角形全等有几种方法?复习引入公理1:三边对应相等的两个三角形全等
(SSS).
公理2:两边及其夹角对应相等的两个三角形全等
( SAS).
公理3:两角及其夹边对应相等的两个三角形全等
(ASA).
推论:两角及其中一角的对边对应相等的两个三角形全等
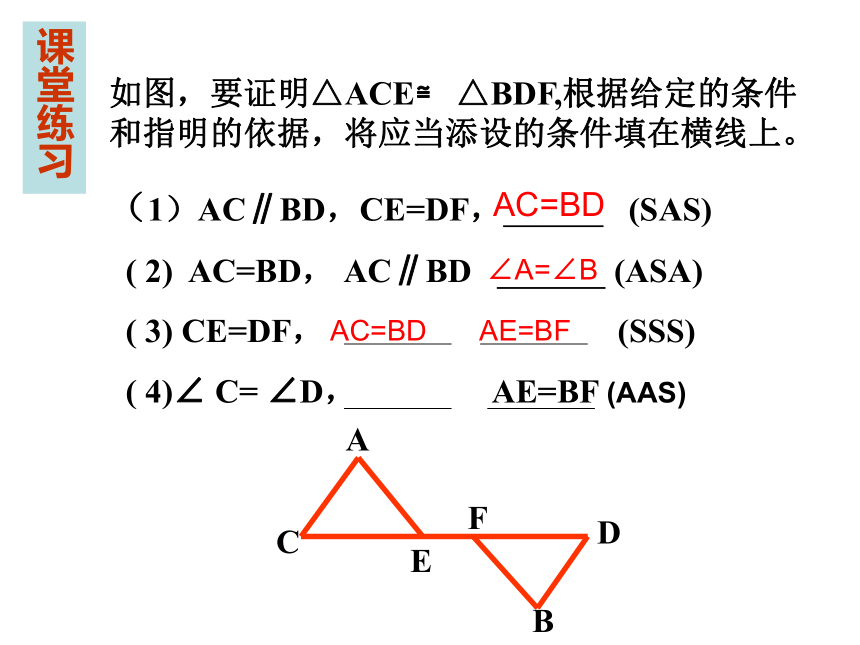
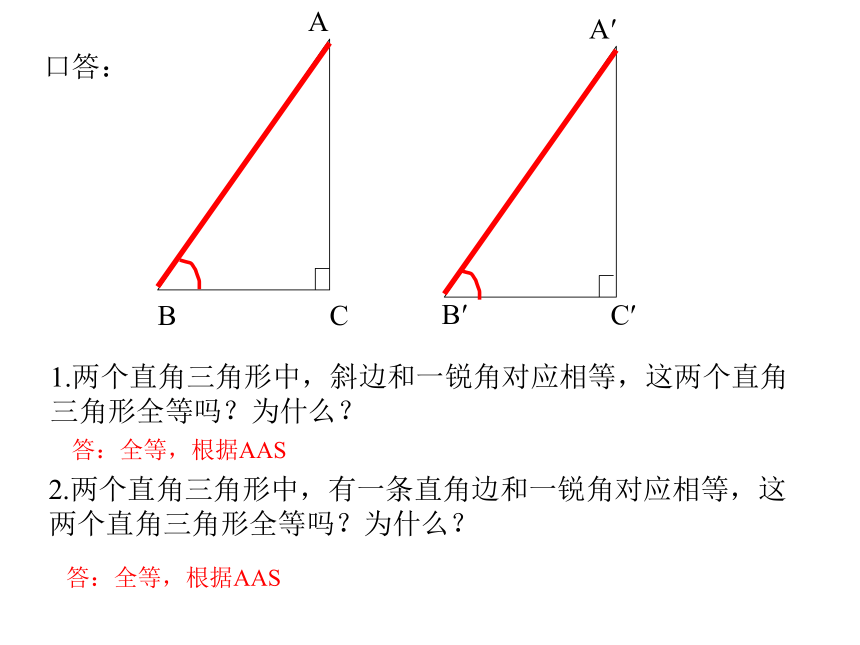
(AAS)如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。课堂练习AC=BD∠A=∠BAC=BDAE=BF 1.两个直角三角形中,斜边和一锐角对应相等,这两个直角
三角形全等吗?为什么?2.两个直角三角形中,有一条直角边和一锐角对应相等,这
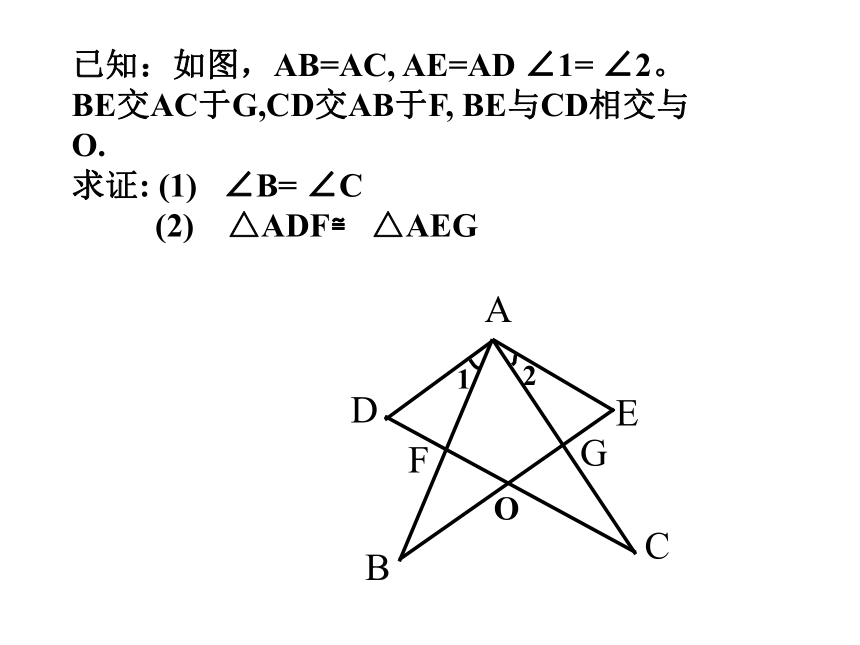
两个直角三角形全等吗?为什么?答:全等,根据AAS答:全等,根据AAS已知:如图,AB=AC, AE=AD ∠1= ∠2。BE交AC于G,CD交AB于F, BE与CD相交与O.
求证: (1) ∠B= ∠C
(2) △ADF≌ △AEG 例2 已知:如图,△ABC≌△A′B′C′,AD、A′D′
分别是△ABC和△A′B′C′的高.
求证:AD = A′D′证明:∵ △ABC≌△A′B′C′
∴AC = A′C′,∠C = ∠C′(?)∵AD⊥BC,A′D′⊥B′C′
∴∠ADC = ∠A′D′C′= 90°在△ADC和△A′D′C′中∠ADC = ∠A′D′C′
∠C = ∠C′
AC = A′C′∴ △ADC≌△A′D′C′
∴AD = A′D′全等三角形的对应边上的高线相等 已知:如图,△ABC≌△A′B′C′,AD、A′D′分别是△ABC和△A′B′C′的对应边上的中线.则AD与A′D′有什么关系?证明你的结论.全等三角形的对应边上的中线相等全等三角形的对应边上的角平分线相等吗?变式1 变式2 提高:
1、如右图:已知,AD、EF、BC交于O,且AO=OD,BO=OC,EO=OF
求证:△AEB≌△DFC
感悟与反思作业:作业本再见
(SSS).
公理2:两边及其夹角对应相等的两个三角形全等
( SAS).
公理3:两角及其夹边对应相等的两个三角形全等
(ASA).
推论:两角及其中一角的对边对应相等的两个三角形全等
(AAS)如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。课堂练习AC=BD∠A=∠BAC=BDAE=BF 1.两个直角三角形中,斜边和一锐角对应相等,这两个直角
三角形全等吗?为什么?2.两个直角三角形中,有一条直角边和一锐角对应相等,这
两个直角三角形全等吗?为什么?答:全等,根据AAS答:全等,根据AAS已知:如图,AB=AC, AE=AD ∠1= ∠2。BE交AC于G,CD交AB于F, BE与CD相交与O.
求证: (1) ∠B= ∠C
(2) △ADF≌ △AEG 例2 已知:如图,△ABC≌△A′B′C′,AD、A′D′
分别是△ABC和△A′B′C′的高.
求证:AD = A′D′证明:∵ △ABC≌△A′B′C′
∴AC = A′C′,∠C = ∠C′(?)∵AD⊥BC,A′D′⊥B′C′
∴∠ADC = ∠A′D′C′= 90°在△ADC和△A′D′C′中∠ADC = ∠A′D′C′
∠C = ∠C′
AC = A′C′∴ △ADC≌△A′D′C′
∴AD = A′D′全等三角形的对应边上的高线相等 已知:如图,△ABC≌△A′B′C′,AD、A′D′分别是△ABC和△A′B′C′的对应边上的中线.则AD与A′D′有什么关系?证明你的结论.全等三角形的对应边上的中线相等全等三角形的对应边上的角平分线相等吗?变式1 变式2 提高:
1、如右图:已知,AD、EF、BC交于O,且AO=OD,BO=OC,EO=OF
求证:△AEB≌△DFC
感悟与反思作业:作业本再见
