沪科版八年级数学上册试题 期末测试卷 (含答案)
文档属性
| 名称 | 沪科版八年级数学上册试题 期末测试卷 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 163.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 00:00:00 | ||
图片预览


文档简介
期末测试卷
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.在平面直角坐标系中,点(﹣2,﹣a2﹣3)一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知正比例函数y=(k+4)x且y随x的增大而减小,则k的取值范围是( )
A.k>4 B.k<4 C.k>4 D.k<﹣4
3.下列函数关系式:①y=﹣2x,②,③y=﹣2x2,④y=2,⑤y=2x﹣1.其中是一次函数的是( )
A.①⑤ B.①④⑤ C.②⑤ D.②④⑤
4.如图,把纸片△ABC的∠A沿DE折叠,点A落在四边形CBDE外,则∠1,∠2与∠A的关系是( )
A.∠2﹣∠1=2∠A B.∠2﹣∠A=2∠1 C.∠1+∠2=2∠A D.∠1+∠A=2∠2
5.若(a﹣1)2+|b﹣2|=0,则以a、b为边长的等腰三角形的周长为( )
A.5 B.4 C.3 D.4或5
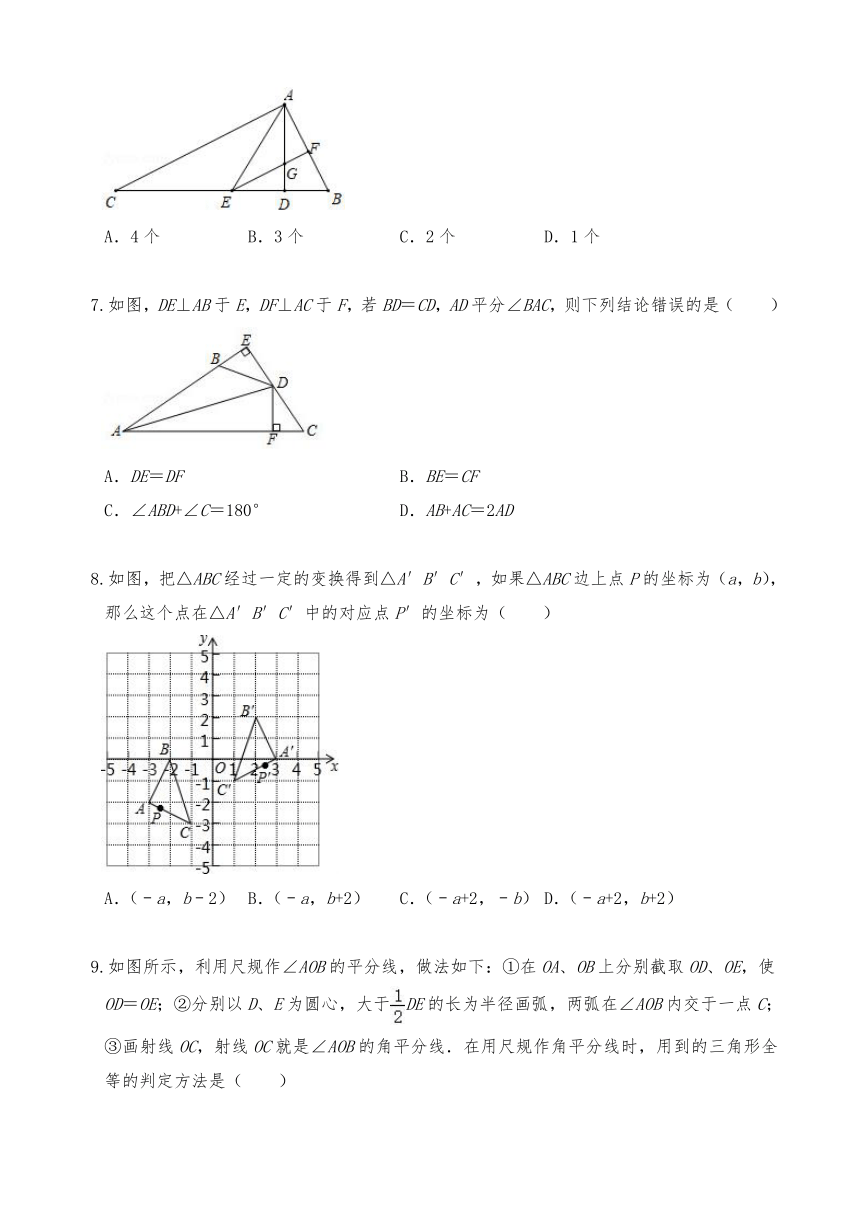
6.如图,在△ABC中,AD是BC边上的高,且∠ACB=∠BAD,AE平分∠CAD,交BC于点E,过点E作EF∥AC,分别交AB、AD于点F、G.则下列结论:①∠BAC=90°;②∠AEF=∠BEF;③∠BAE=∠BEA;④∠B=2∠AEF,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
7.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,AD平分∠BAC,则下列结论错误的是( )
A.DE=DF B.BE=CF
C.∠ABD+∠C=180° D.AB+AC=2AD
8.如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )
A.(﹣a,b﹣2) B.(﹣a,b+2) C.(﹣a+2,﹣b) D.(﹣a+2,b+2)
9.如图所示,利用尺规作∠AOB的平分线,做法如下:①在OA、OB上分别截取OD、OE,使OD=OE;②分别以D、E为圆心,大于DE的长为半径画弧,两弧在∠AOB内交于一点C;③画射线OC,射线OC就是∠AOB的角平分线.在用尺规作角平分线时,用到的三角形全等的判定方法是( )
A.SSS B.ASA C.AAS D.SAS
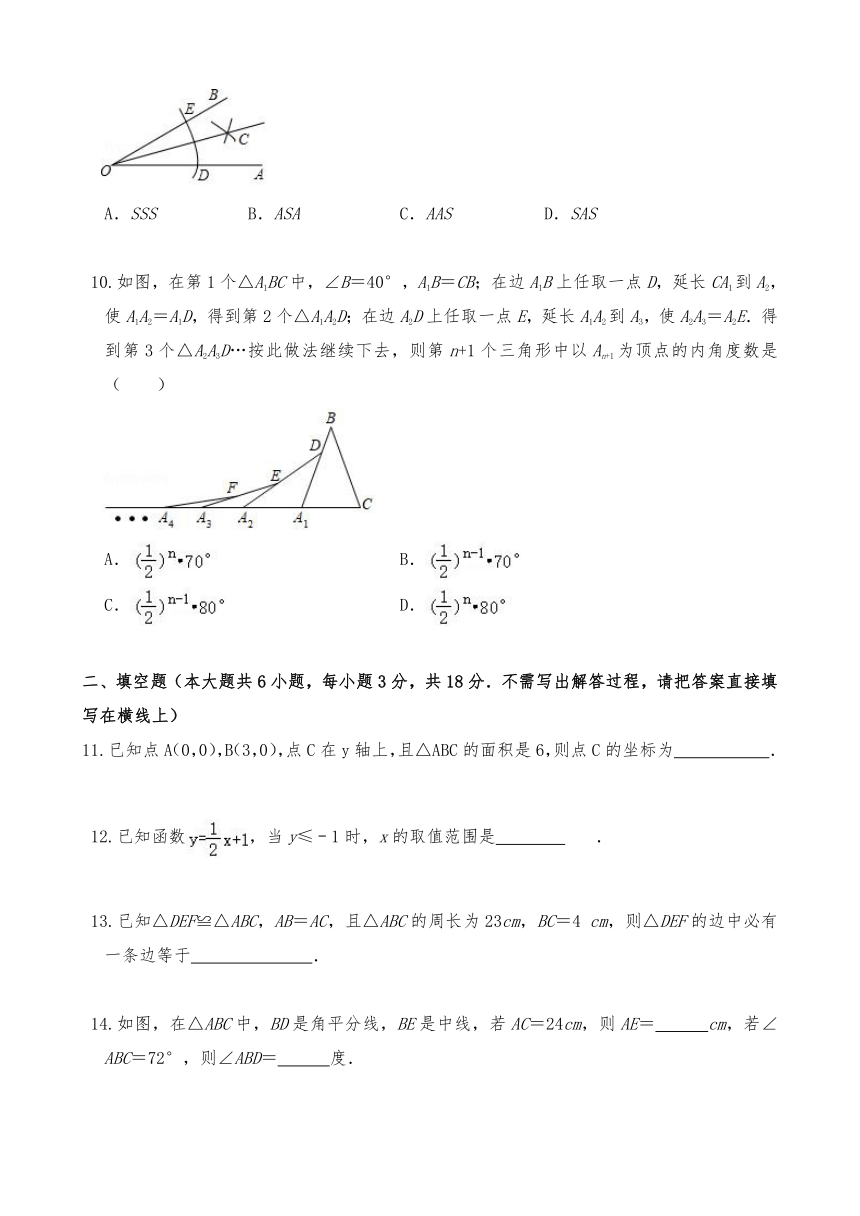
10.如图,在第1个△A1BC中,∠B=40°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E.得到第3个△A2A3D…按此做法继续下去,则第n+1个三角形中以An+1为顶点的内角度数是( )
A. B.
C. D.
二、填空题(本大题共6小题,每小题3分,共18分.不需写出解答过程,请把答案直接填写在横线上)
11.已知点A(0,0),B(3,0),点C在y轴上,且△ABC的面积是6,则点C的坐标为 .
12.已知函数,当y≤﹣1时,x的取值范围是 .
13.已知△DEF≌△ABC,AB=AC,且△ABC的周长为23cm,BC=4 cm,则△DEF的边中必有一条边等于 .
14.如图,在△ABC中,BD是角平分线,BE是中线,若AC=24cm,则AE= cm,若∠ABC=72°,则∠ABD= 度.
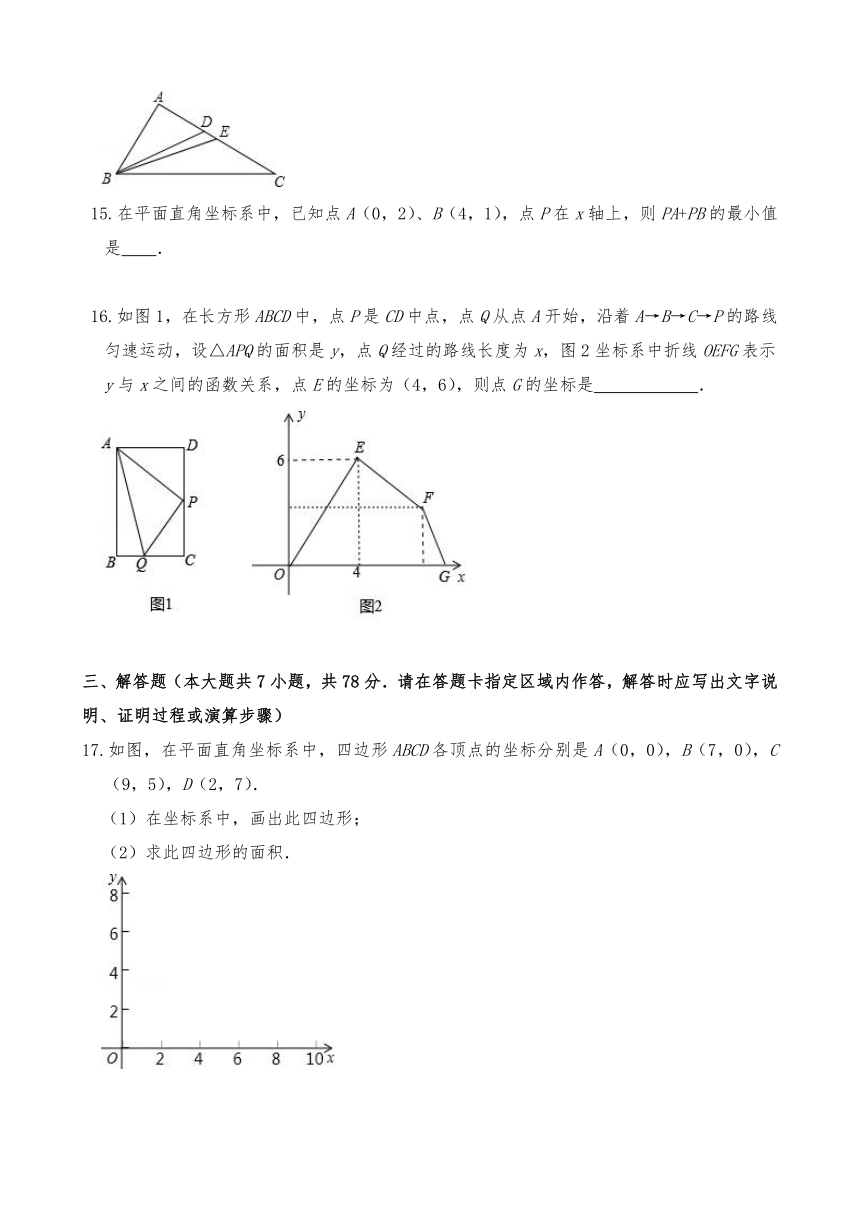
15.在平面直角坐标系中,已知点A(0,2)、B(4,1),点P在x轴上,则PA+PB的最小值是 .
16.如图1,在长方形ABCD中,点P是CD中点,点Q从点A开始,沿着A→B→C→P的路线匀速运动,设△APQ的面积是y,点Q经过的路线长度为x,图2坐标系中折线OEFG表示y与x之间的函数关系,点E的坐标为(4,6),则点G的坐标是 .
三、解答题(本大题共7小题,共78分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
17.如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别是A(0,0),B(7,0),C(9,5),D(2,7).
(1)在坐标系中,画出此四边形;
(2)求此四边形的面积.
18.若关于x,y的二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求m的值.
19.如图,∠A=∠B=50°,P为AB的中点,点E为射线AC上(不与点A重合)的任意一点,连结EP,并使EP的延长线交射线BD于点F.
(1)求证:△APE≌△BPF.
(2)当EF=2BF时,求∠BFP的度数.
20.如图,C,D是AB的垂直平分线上两点,延长AC,DB交于点E,AF∥BC交DE于点F.求证:
(1)AB是∠CAF的角平分线;
(2)∠FAD=∠E.
21.如图,在△ABC中,AB=AC,∠BAC=80°,D是AC上一点,E是BC延长线上一点,连接BD,DE,若∠ABD=20°,BD=DE,求∠CDE的度数.
22.如图,在平面直角坐标系中,直线l1:y=﹣x+b与直线l2:y=kx相交于点B(m,﹣4),直线l1与x轴交于点A(﹣6,0).
(1)求b,m,k的值;
(2)若第一象限内有一点P(3,2),连接AP,BP,求△ABP的面积;
(3)在直线l2上是否存在一点Q,使得以A,B,Q为顶点的三角形为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
23.如图,已知A(﹣3,2),B(2,0),点C为x轴负半轴上一点.
(1)若△ABC的面积为4,求C点的坐标;
(2)若将△ABC沿x轴折叠,使点A落在点D处;
①写出D点的坐标并求A、D两点之间的距离;
②延长DC交AB于点E,EF平分∠AED交x轴于点F,若∠ACF﹣∠AEF=15°,求∠EFB的度数;
(3)过点C作MN平行于AB交y轴于点H,CP、HP分别平行∠BCM和∠AHQ,当点C在x轴负半轴上运动时,∠CPH的度数是否发生变化?若不变求其度数;若变化,求其变化范围.
答案
一、选择题
C.D.A.A.A.B.D.B.A.A.
二、填空题
11.(0,4)(0,﹣4)
12.x≤﹣4.
13.4cm或9.5cm.
14.12,36.
15.5.
16.(9,0).
三、解答题
17.解:(1)四边形ABCD如图所示;
(2)四边形的面积=9×7﹣×2×7﹣×2×5﹣×2×7,
=63﹣7﹣5﹣7,
=63﹣19,
=44.
18.解:,
②×2﹣①得:x=m﹣1,
①×2﹣②得:y=2,
(1)当y=2为底,x为腰,x=3.5,可以组成三角形,m﹣1=(9﹣2)÷2,
m=4.5;
(2)x=m﹣1是底,y=2是腰
2y+x=9,得m=6,
x=5,y=2构不成三角形,
所以m=6舍去,
综上所述:m的值为4.5.
19.解:(1)证明:∵P是AB的中点,
∴PA=PB,
在△APE和△BPF中,
∴△APE≌△BPF(ASA);
(2)由(1)得:△APE≌△BPF,
∴PE=PF,
∴EF=2PF,
∵EF=2BF,
∴BF=PF,
∴α=∠B=50°.
20.证明:(1)∵点C是AB的垂直平分线上的点,
∴CB=CA,
∴∠CBA=∠CAB,
∵AF∥BC交DE于点F,
∴∠BAF=∠CBA,
∴∠BAF=∠CAB.
即 AB是∠CAF的角平分线.
(2)∵点D是AB的垂直平分线上的点,
∴DB=DA,
∴∠DBA=∠DAB,
∵∠DBA=∠E+∠CAB,∠DAB=∠FAD+∠BAF,∠CAB=∠BAF,
∴∠E=∠FAD.
21.解:∵在△ABC中,AB=AC,∠BAC=80°,
∴∠ABC=∠ACB=(180°﹣80°)=50°,
∵∠ABD=20°,
∴∠DBC=∠ABC﹣∠ABD=30°.
∵BD=DE,
∴∠E=∠DBC=30°,
∴∠CDE=∠ACB﹣∠E=20°.
22.解:(1)将点A坐标代入直线l1:0=﹣×(﹣6)+b,解得:b=﹣3,
直线l1:y=﹣x﹣3,
将点B的坐标代入上式并解得:m=2,即点B(2,﹣4),
将点B的坐标代入直线l2:y=kx并解得:k=﹣2,
直线l2:y=﹣2x,
故:b=﹣3,m=2,k=﹣2;
(2)设直线PB交x轴于点H,
由点PB的坐标,同理可得直线PB的表达式为:y=6x﹣16,
则点H(,0),
S△ABP=×AH×(yP﹣yB)=×(6+)×6=26;
(3)设点Q(n,﹣2n),
则AB2=80,BQ2=(n﹣2)2+(4﹣2n)2,AQ2=(n+6)2+4n2;
①当AB=BQ时,
即80=(n﹣2)2+(4﹣2n)2,解得:n=6或﹣2;
②当AB=AQ时,
同理可得:n=2或﹣;
③当AQ=BQ时,
同理可得:n=﹣,
综上,点Q的坐标为:(6,﹣12)或(﹣2,4)或(2,﹣4)或(﹣,)或(﹣,1).
23.解:(1)∵△ABC的面积为4,
∴ 2 BC=4,
∴BC=4,
而OB=2,
∴OC=2,
∴C点坐标为(﹣2,0);
(2)①∵△ABC沿x轴折叠,使点A落在点D处,
∴点D与点A关于x轴对称,
∴D点坐标为(﹣3,﹣2);
∴AD=2﹣(﹣2)=4;
②∵△ABC沿x轴折叠,使点A落在点D处,
∴∠DCF=∠ACF,
而∠DCF=∠EFB+∠DEF,
∴∠EFB=∠ACF﹣∠DEF,
∵EF平分∠AED,
∴∠DEF=∠AEF,
∴∠EFB=∠ACF﹣∠AEF=15°;
(3)∠CPH=45°.理由如下:
如图2,
∵MN∥AB,
∴∠MCP=∠1,∠AHQ=∠3,
∵CP、HP分别平行∠BCM和∠AHQ,
∴∠MCP=∠BCM,∠2=∠AHQ,
∴∠1=∠BCM,∠2=∠3,
∵∠BCM=90°+∠3,
∴2∠1=90°+2∠2,即∠1=45°+∠2,
∵∠1=∠CPH+∠2,
∴∠CPH=45°.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.在平面直角坐标系中,点(﹣2,﹣a2﹣3)一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知正比例函数y=(k+4)x且y随x的增大而减小,则k的取值范围是( )
A.k>4 B.k<4 C.k>4 D.k<﹣4
3.下列函数关系式:①y=﹣2x,②,③y=﹣2x2,④y=2,⑤y=2x﹣1.其中是一次函数的是( )
A.①⑤ B.①④⑤ C.②⑤ D.②④⑤
4.如图,把纸片△ABC的∠A沿DE折叠,点A落在四边形CBDE外,则∠1,∠2与∠A的关系是( )
A.∠2﹣∠1=2∠A B.∠2﹣∠A=2∠1 C.∠1+∠2=2∠A D.∠1+∠A=2∠2
5.若(a﹣1)2+|b﹣2|=0,则以a、b为边长的等腰三角形的周长为( )
A.5 B.4 C.3 D.4或5
6.如图,在△ABC中,AD是BC边上的高,且∠ACB=∠BAD,AE平分∠CAD,交BC于点E,过点E作EF∥AC,分别交AB、AD于点F、G.则下列结论:①∠BAC=90°;②∠AEF=∠BEF;③∠BAE=∠BEA;④∠B=2∠AEF,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
7.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,AD平分∠BAC,则下列结论错误的是( )
A.DE=DF B.BE=CF
C.∠ABD+∠C=180° D.AB+AC=2AD
8.如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )
A.(﹣a,b﹣2) B.(﹣a,b+2) C.(﹣a+2,﹣b) D.(﹣a+2,b+2)
9.如图所示,利用尺规作∠AOB的平分线,做法如下:①在OA、OB上分别截取OD、OE,使OD=OE;②分别以D、E为圆心,大于DE的长为半径画弧,两弧在∠AOB内交于一点C;③画射线OC,射线OC就是∠AOB的角平分线.在用尺规作角平分线时,用到的三角形全等的判定方法是( )
A.SSS B.ASA C.AAS D.SAS
10.如图,在第1个△A1BC中,∠B=40°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E.得到第3个△A2A3D…按此做法继续下去,则第n+1个三角形中以An+1为顶点的内角度数是( )
A. B.
C. D.
二、填空题(本大题共6小题,每小题3分,共18分.不需写出解答过程,请把答案直接填写在横线上)
11.已知点A(0,0),B(3,0),点C在y轴上,且△ABC的面积是6,则点C的坐标为 .
12.已知函数,当y≤﹣1时,x的取值范围是 .
13.已知△DEF≌△ABC,AB=AC,且△ABC的周长为23cm,BC=4 cm,则△DEF的边中必有一条边等于 .
14.如图,在△ABC中,BD是角平分线,BE是中线,若AC=24cm,则AE= cm,若∠ABC=72°,则∠ABD= 度.
15.在平面直角坐标系中,已知点A(0,2)、B(4,1),点P在x轴上,则PA+PB的最小值是 .
16.如图1,在长方形ABCD中,点P是CD中点,点Q从点A开始,沿着A→B→C→P的路线匀速运动,设△APQ的面积是y,点Q经过的路线长度为x,图2坐标系中折线OEFG表示y与x之间的函数关系,点E的坐标为(4,6),则点G的坐标是 .
三、解答题(本大题共7小题,共78分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
17.如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别是A(0,0),B(7,0),C(9,5),D(2,7).
(1)在坐标系中,画出此四边形;
(2)求此四边形的面积.
18.若关于x,y的二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求m的值.
19.如图,∠A=∠B=50°,P为AB的中点,点E为射线AC上(不与点A重合)的任意一点,连结EP,并使EP的延长线交射线BD于点F.
(1)求证:△APE≌△BPF.
(2)当EF=2BF时,求∠BFP的度数.
20.如图,C,D是AB的垂直平分线上两点,延长AC,DB交于点E,AF∥BC交DE于点F.求证:
(1)AB是∠CAF的角平分线;
(2)∠FAD=∠E.
21.如图,在△ABC中,AB=AC,∠BAC=80°,D是AC上一点,E是BC延长线上一点,连接BD,DE,若∠ABD=20°,BD=DE,求∠CDE的度数.
22.如图,在平面直角坐标系中,直线l1:y=﹣x+b与直线l2:y=kx相交于点B(m,﹣4),直线l1与x轴交于点A(﹣6,0).
(1)求b,m,k的值;
(2)若第一象限内有一点P(3,2),连接AP,BP,求△ABP的面积;
(3)在直线l2上是否存在一点Q,使得以A,B,Q为顶点的三角形为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
23.如图,已知A(﹣3,2),B(2,0),点C为x轴负半轴上一点.
(1)若△ABC的面积为4,求C点的坐标;
(2)若将△ABC沿x轴折叠,使点A落在点D处;
①写出D点的坐标并求A、D两点之间的距离;
②延长DC交AB于点E,EF平分∠AED交x轴于点F,若∠ACF﹣∠AEF=15°,求∠EFB的度数;
(3)过点C作MN平行于AB交y轴于点H,CP、HP分别平行∠BCM和∠AHQ,当点C在x轴负半轴上运动时,∠CPH的度数是否发生变化?若不变求其度数;若变化,求其变化范围.
答案
一、选择题
C.D.A.A.A.B.D.B.A.A.
二、填空题
11.(0,4)(0,﹣4)
12.x≤﹣4.
13.4cm或9.5cm.
14.12,36.
15.5.
16.(9,0).
三、解答题
17.解:(1)四边形ABCD如图所示;
(2)四边形的面积=9×7﹣×2×7﹣×2×5﹣×2×7,
=63﹣7﹣5﹣7,
=63﹣19,
=44.
18.解:,
②×2﹣①得:x=m﹣1,
①×2﹣②得:y=2,
(1)当y=2为底,x为腰,x=3.5,可以组成三角形,m﹣1=(9﹣2)÷2,
m=4.5;
(2)x=m﹣1是底,y=2是腰
2y+x=9,得m=6,
x=5,y=2构不成三角形,
所以m=6舍去,
综上所述:m的值为4.5.
19.解:(1)证明:∵P是AB的中点,
∴PA=PB,
在△APE和△BPF中,
∴△APE≌△BPF(ASA);
(2)由(1)得:△APE≌△BPF,
∴PE=PF,
∴EF=2PF,
∵EF=2BF,
∴BF=PF,
∴α=∠B=50°.
20.证明:(1)∵点C是AB的垂直平分线上的点,
∴CB=CA,
∴∠CBA=∠CAB,
∵AF∥BC交DE于点F,
∴∠BAF=∠CBA,
∴∠BAF=∠CAB.
即 AB是∠CAF的角平分线.
(2)∵点D是AB的垂直平分线上的点,
∴DB=DA,
∴∠DBA=∠DAB,
∵∠DBA=∠E+∠CAB,∠DAB=∠FAD+∠BAF,∠CAB=∠BAF,
∴∠E=∠FAD.
21.解:∵在△ABC中,AB=AC,∠BAC=80°,
∴∠ABC=∠ACB=(180°﹣80°)=50°,
∵∠ABD=20°,
∴∠DBC=∠ABC﹣∠ABD=30°.
∵BD=DE,
∴∠E=∠DBC=30°,
∴∠CDE=∠ACB﹣∠E=20°.
22.解:(1)将点A坐标代入直线l1:0=﹣×(﹣6)+b,解得:b=﹣3,
直线l1:y=﹣x﹣3,
将点B的坐标代入上式并解得:m=2,即点B(2,﹣4),
将点B的坐标代入直线l2:y=kx并解得:k=﹣2,
直线l2:y=﹣2x,
故:b=﹣3,m=2,k=﹣2;
(2)设直线PB交x轴于点H,
由点PB的坐标,同理可得直线PB的表达式为:y=6x﹣16,
则点H(,0),
S△ABP=×AH×(yP﹣yB)=×(6+)×6=26;
(3)设点Q(n,﹣2n),
则AB2=80,BQ2=(n﹣2)2+(4﹣2n)2,AQ2=(n+6)2+4n2;
①当AB=BQ时,
即80=(n﹣2)2+(4﹣2n)2,解得:n=6或﹣2;
②当AB=AQ时,
同理可得:n=2或﹣;
③当AQ=BQ时,
同理可得:n=﹣,
综上,点Q的坐标为:(6,﹣12)或(﹣2,4)或(2,﹣4)或(﹣,)或(﹣,1).
23.解:(1)∵△ABC的面积为4,
∴ 2 BC=4,
∴BC=4,
而OB=2,
∴OC=2,
∴C点坐标为(﹣2,0);
(2)①∵△ABC沿x轴折叠,使点A落在点D处,
∴点D与点A关于x轴对称,
∴D点坐标为(﹣3,﹣2);
∴AD=2﹣(﹣2)=4;
②∵△ABC沿x轴折叠,使点A落在点D处,
∴∠DCF=∠ACF,
而∠DCF=∠EFB+∠DEF,
∴∠EFB=∠ACF﹣∠DEF,
∵EF平分∠AED,
∴∠DEF=∠AEF,
∴∠EFB=∠ACF﹣∠AEF=15°;
(3)∠CPH=45°.理由如下:
如图2,
∵MN∥AB,
∴∠MCP=∠1,∠AHQ=∠3,
∵CP、HP分别平行∠BCM和∠AHQ,
∴∠MCP=∠BCM,∠2=∠AHQ,
∴∠1=∠BCM,∠2=∠3,
∵∠BCM=90°+∠3,
∴2∠1=90°+2∠2,即∠1=45°+∠2,
∵∠1=∠CPH+∠2,
∴∠CPH=45°.
同课章节目录
