全等三角形(复习)[上学期]
文档属性
| 名称 | 全等三角形(复习)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 669.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-16 00:00:00 | ||
图片预览




文档简介
课件12张PPT。三角形的复习
蒲元初中:蒲元初中:蒲元初中:全等三角形
(1)两个能够完全重合的三角形叫全等三角形,
(2)全等三角形的对应角相等,对应边相等。
(3)判定两个三角形全等的公理或定理:
①一般三角形有
SSS、SAS、ASA 、AAS②千万不要将SSA条件作为SAS条件来用。
1。证明两个三角形全等,要结合题目的条件和结论,选择恰当的判定方法 2。全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时 ①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
选择三角形全等的五种方法(“SSS”、“SAS”、“ASA”、“AAS”,“HL”)中,至少有一组相等的边,因此在应用时要养成先找边的习惯;如果先找到了一组对应边,再找第二组条件,若找到一组对应边则再找这两边的夹角用“SAS”或再找第三组对应边用“SSS”;若找到一组角则需找另一组角,(可能用“ASA”或“AAS”)或夹这个角的另一组对应边用“SAS”;若是判定两个直角三角形全等则优先考虑“HL”,上述思路可归纳为下面的思维图:总之,证明过程中能用简单方法的就不要绕弯路。SS
AA(用SAS)
S(用SSS)S(用SAS)
A
用AAS
或ASA
A D
E
F
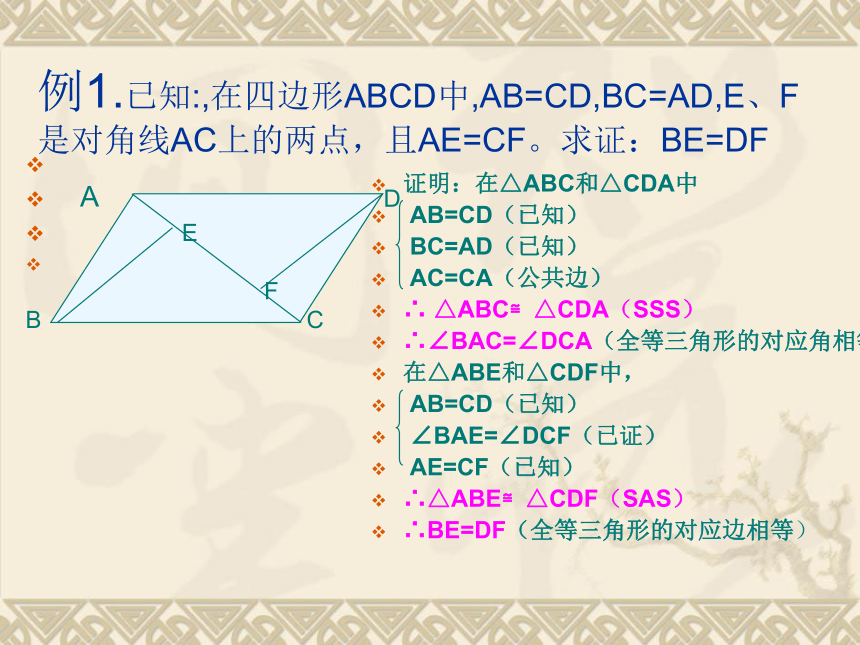
B C 例1.已知:,在四边形ABCD中,AB=CD,BC=AD,E、F 是对角线AC上的两点,且AE=CF。求证:BE=DF证明:在△ABC和△CDA中
AB=CD(已知)
BC=AD(已知)
AC=CA(公共边)
∴ △ABC≌△CDA(SSS)
∴∠BAC=∠DCA(全等三角形的对应角相等)
在△ABE和△CDF中,
AB=CD(已知)
∠BAE=∠DCF(已证)
AE=CF(已知)
∴△ABE≌△CDF(SAS)
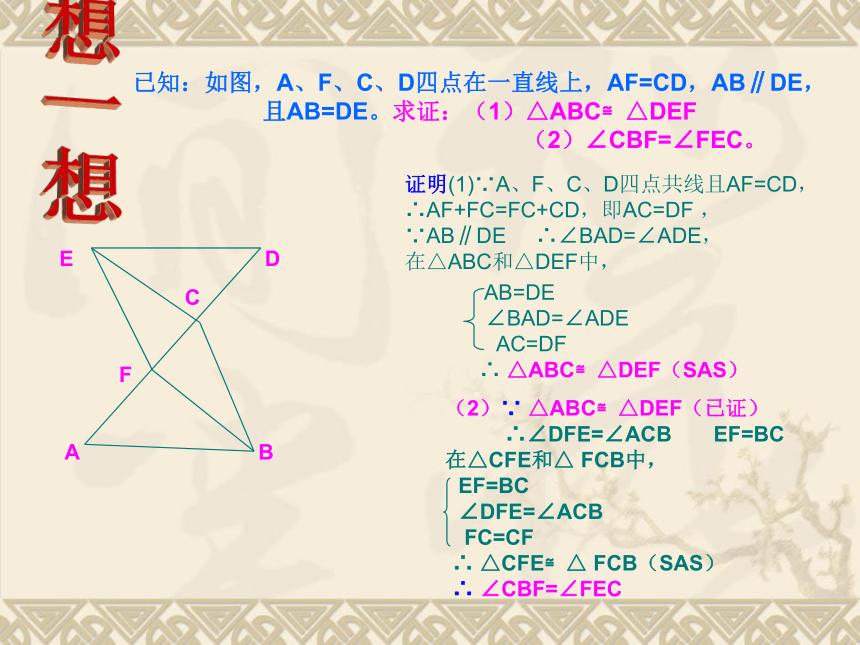
∴BE=DF(全等三角形的对应边相等)已知:如图,A、F、C、D四点在一直线上,AF=CD,AB∥DE,且AB=DE。求证:(1)△ABC≌△DEF (2)∠CBF=∠FEC。
想一想
证明(1)∵A、F、C、D四点共线且AF=CD, ∴AF+FC=FC+CD,即AC=DF ,
∵AB∥DE ∴∠BAD=∠ADE,
在△ABC和△DEF中,
AB=DE
∠BAD=∠ADE
AC=DF
∴ △ABC≌△DEF(SAS)(2)∵ △ABC≌△DEF(已证)
∴∠DFE=∠ACB EF=BC
在△CFE和△ FCB中,
E D
C
F
A B EF=BC
∠DFE=∠ACB
FC=CF
∴ △CFE≌△ FCB(SAS)
∴ ∠CBF=∠FEC
例2、如图,已知AB=AC,AD=AE,AB、DC相交于点M,AC、BE相交于点N,∠1=∠2,求证(1) △ABE ≌ △ADC (2)AM=AN
A
1
2
D E
M N
B C
1)证明:∵ ∠ 1=∠2(已知)
∴ ∠ 1+ ∠ BAC= ∠ 2+ ∠BAC
即∠ DAC= ∠BAE
在△ ABE和△ACD中
∴ △ABE ≌ △ACD(SAS)(2)∵ △ABE ≌ △ACD(已证)
∴∠D = ∠E(全等三角形的对应角相等)
∴ △ADM≌△AEN(ASA)
∴ AM=AN(全等三角形的对应边相等)如图,已知:AB=CD,AC=DB,求证(1)∠B=∠C (2)OA=OD
A D
O
B C练一练如图线段AB是一个池塘的长度,
现在想测量这个池塘的长度,在
水上测量不方便,你有什么好的
方法较方便地把池塘的长度测量
出来吗?想想看。AB探
究 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。 AC=DC?
∠ACB=∠DCE
BC=EC △ACB≌△DCE(SAS)
AB=DEECBAD解:在△ACB和△DCE中,(全等三角形对应边相等。)作业: A
E
O
B D C A
D E
B C1、如图:已知△ABC中,延长AC边上的中线BE到G,使EG=BE,延长AB边上的中线CD到F,使DF=CD,连接AF、AG。
①补全图形;
②AF与AG的大小关系如何?写出你的判断根据;
③F、A、G三点的位置关系如何?请说出理由。
2、如图:在△ABC中,∠ABC=60,AD、CE分别平分∠BAC,∠ACB,求证:AC=AE+CD
再 见祝同学们学习进步
蒲元初中:蒲元初中:蒲元初中:全等三角形
(1)两个能够完全重合的三角形叫全等三角形,
(2)全等三角形的对应角相等,对应边相等。
(3)判定两个三角形全等的公理或定理:
①一般三角形有
SSS、SAS、ASA 、AAS②千万不要将SSA条件作为SAS条件来用。
1。证明两个三角形全等,要结合题目的条件和结论,选择恰当的判定方法 2。全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时 ①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
选择三角形全等的五种方法(“SSS”、“SAS”、“ASA”、“AAS”,“HL”)中,至少有一组相等的边,因此在应用时要养成先找边的习惯;如果先找到了一组对应边,再找第二组条件,若找到一组对应边则再找这两边的夹角用“SAS”或再找第三组对应边用“SSS”;若找到一组角则需找另一组角,(可能用“ASA”或“AAS”)或夹这个角的另一组对应边用“SAS”;若是判定两个直角三角形全等则优先考虑“HL”,上述思路可归纳为下面的思维图:总之,证明过程中能用简单方法的就不要绕弯路。SS
AA(用SAS)
S(用SSS)S(用SAS)
A
用AAS
或ASA
A D
E
F
B C 例1.已知:,在四边形ABCD中,AB=CD,BC=AD,E、F 是对角线AC上的两点,且AE=CF。求证:BE=DF证明:在△ABC和△CDA中
AB=CD(已知)
BC=AD(已知)
AC=CA(公共边)
∴ △ABC≌△CDA(SSS)
∴∠BAC=∠DCA(全等三角形的对应角相等)
在△ABE和△CDF中,
AB=CD(已知)
∠BAE=∠DCF(已证)
AE=CF(已知)
∴△ABE≌△CDF(SAS)
∴BE=DF(全等三角形的对应边相等)已知:如图,A、F、C、D四点在一直线上,AF=CD,AB∥DE,且AB=DE。求证:(1)△ABC≌△DEF (2)∠CBF=∠FEC。
想一想
证明(1)∵A、F、C、D四点共线且AF=CD, ∴AF+FC=FC+CD,即AC=DF ,
∵AB∥DE ∴∠BAD=∠ADE,
在△ABC和△DEF中,
AB=DE
∠BAD=∠ADE
AC=DF
∴ △ABC≌△DEF(SAS)(2)∵ △ABC≌△DEF(已证)
∴∠DFE=∠ACB EF=BC
在△CFE和△ FCB中,
E D
C
F
A B EF=BC
∠DFE=∠ACB
FC=CF
∴ △CFE≌△ FCB(SAS)
∴ ∠CBF=∠FEC
例2、如图,已知AB=AC,AD=AE,AB、DC相交于点M,AC、BE相交于点N,∠1=∠2,求证(1) △ABE ≌ △ADC (2)AM=AN
A
1
2
D E
M N
B C
1)证明:∵ ∠ 1=∠2(已知)
∴ ∠ 1+ ∠ BAC= ∠ 2+ ∠BAC
即∠ DAC= ∠BAE
在△ ABE和△ACD中
∴ △ABE ≌ △ACD(SAS)(2)∵ △ABE ≌ △ACD(已证)
∴∠D = ∠E(全等三角形的对应角相等)
∴ △ADM≌△AEN(ASA)
∴ AM=AN(全等三角形的对应边相等)如图,已知:AB=CD,AC=DB,求证(1)∠B=∠C (2)OA=OD
A D
O
B C练一练如图线段AB是一个池塘的长度,
现在想测量这个池塘的长度,在
水上测量不方便,你有什么好的
方法较方便地把池塘的长度测量
出来吗?想想看。AB探
究 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。 AC=DC?
∠ACB=∠DCE
BC=EC △ACB≌△DCE(SAS)
AB=DEECBAD解:在△ACB和△DCE中,(全等三角形对应边相等。)作业: A
E
O
B D C A
D E
B C1、如图:已知△ABC中,延长AC边上的中线BE到G,使EG=BE,延长AB边上的中线CD到F,使DF=CD,连接AF、AG。
①补全图形;
②AF与AG的大小关系如何?写出你的判断根据;
③F、A、G三点的位置关系如何?请说出理由。
2、如图:在△ABC中,∠ABC=60,AD、CE分别平分∠BAC,∠ACB,求证:AC=AE+CD
再 见祝同学们学习进步
