4.1 函数 课件(共50张PPT）

(共50张PPT)
第四章 一次函数
第1课时 函数
1.在一个变化过程中，我们称数值发生变化的量为变量，数值始终不变的量为常量.
知识回顾
2.判断一个量是常量还是变量的方法:
看这个量在某一变化过程中的值是否发生改变（或者说是否会取不同的数值），若在变化过程中此量的数值不变，则此量是常量，若此量可以取不同的数值，则次量是变量.
在三角形ABC中，底边为 x，底边上的高为 y，面积为S=xy，当底边 x 为定值时，下列描述正确的是（ ）.
A. S，y，x是变量， 是常量.
B. S，y是变量， x， 是常量.
C. Y，x是变量，S 是常量.
D. S是变量， y ， x， 是常量.
B
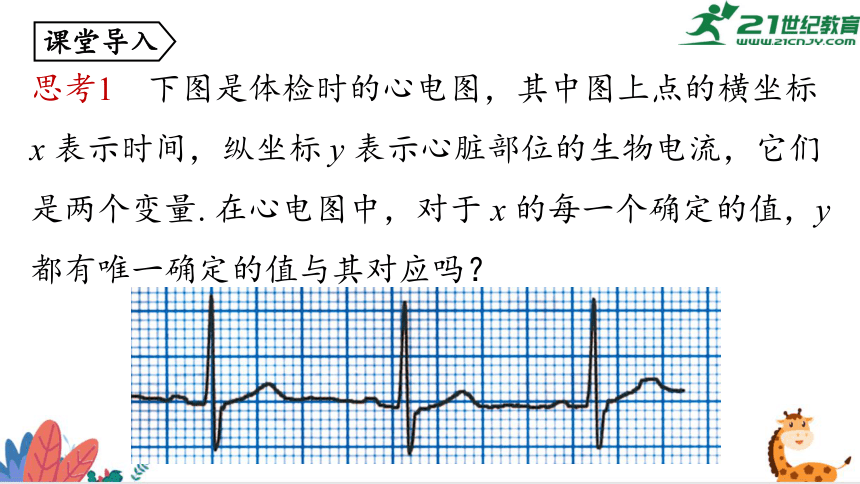
思考1 下图是体检时的心电图，其中图上点的横坐标 x 表示时间，纵坐标 y 表示心脏部位的生物电流，它们是两个变量. 在心电图中，对于 x 的每一个确定的值，y 都有唯一确定的值与其对应吗？
课堂导入
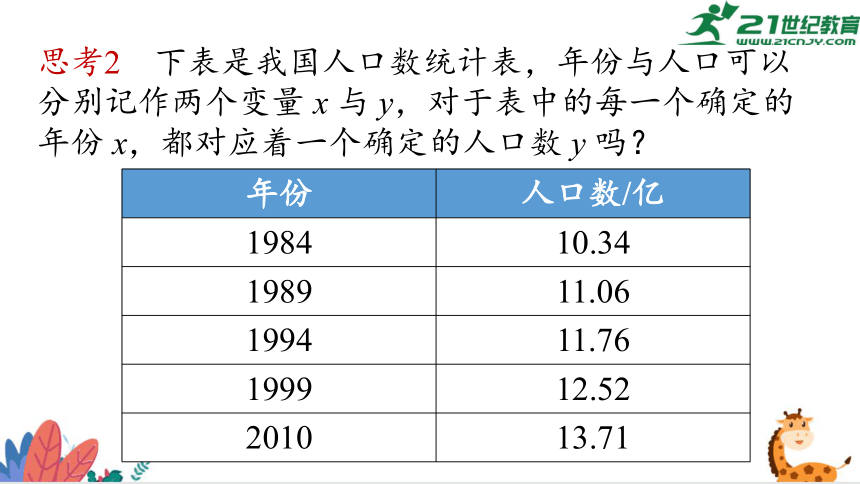
思考2 下表是我国人口数统计表，年份与人口可以分别记作两个变量 x 与 y，对于表中的每一个确定的年份 x，都对应着一个确定的人口数 y 吗？
年份 人口数/亿
1984 10.34
1989 11.06
1994 11.76
1999 12.52
2010 13.71
那么，对于这样的关系我们该怎样定义呢？x 和 y 又分别代表什么含义呢？
我们发现：在上述两个思考问题的变化过程中，都有两个变量 x 与 y ，并且对于x的每一个确定的值， y 都有唯一确定的值与其对应.
1.函数 一般地，在一个变化过程中，如果有两个变量 x与 y，并且对于 x 的每一个确定的值，y 都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数.
知识点01：函数的概念
新知探究
2.判断一个关系是否是函数关系的方法
（1）看是否在一个变化过程中；
（2）看是否存在两个变量；
（3）看每当变量取定一个值时，另外一个变量是否都有唯一确定的值与其相对应.
三个条件缺一不可！
注意：
（1）函数具有唯一对应性.判断两个变量是否具有函数关系，不能只看是否有关系式存在，还要看对于给定x的每一个值，y是否有唯一确定的值与其对应.如在y=± x中，y就不是x的函数.
（2）函数具有相互依存性.函数是一个变量相对于另一个变量而言的，如对于两个变量x与y，y是x的函数.
（3）函数具有顺序性.如y=x+3表示y是x的函数，而变化后的等式x=2y-6表示x是y的函数.
1.小明向平静的池塘水面扔一颗石头，在水面形成了圆形水波. 当圆形水波的半径从2cm扩大成6cm时，圆形水波的面积从 变成了 .在这一变化过程中， 是自变量， 是自变量的函数.
4π
36π
半径
面积
跟踪训练
新知探究
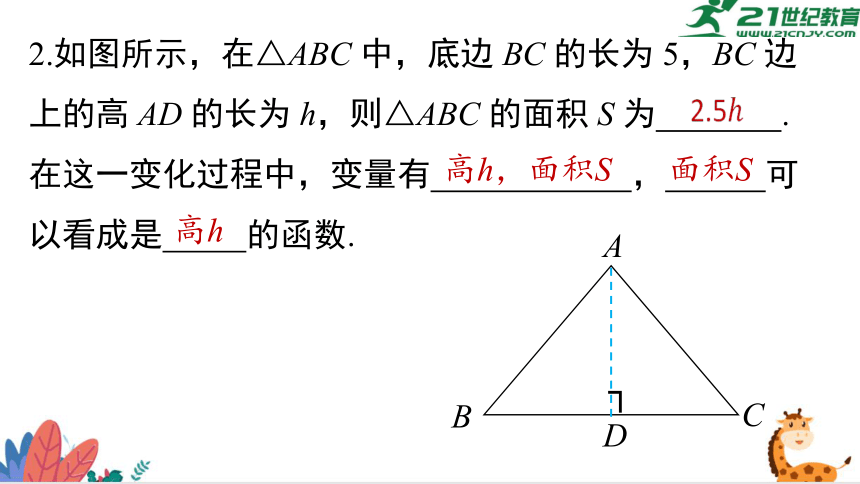
2.如图所示，在△ABC 中，底边 BC 的长为 5，BC 边上的高 AD 的长为 h，则△ABC 的面积 S 为 .在这一变化过程中，变量有 ， 可以看成是 的函数.
A
B
C
D
┐
2.5
高h，面积S
面积S
高h
函数自变量的取值范围 使函数关系式有意义的自变量取值的全体叫做自变量的取值范围.
注意：1.当用函数关系表示实际问题时，自变量的取值不仅要使函数关系式有意义，还应该使实际问题有意义.
2.当函数关系式中有分式、二次根式、零指数幂等情况时，自变量的取值范围一定要满足每一种情况.
知识点02：函数自变量的取值范围
新知探究
1.整式型 等号右边是整式，自变量的取值范围是全体实数，例如：.
2.分式型 等号右边的自变量在分母的位置上，自变量的取值范围是使分母不为0的实数，例如：.
不同类型函数自变量取值范围的确定
3.根式型 等号右边是开偶次方的式子，自变量的取值范围是使根号下的式子的值大于或等于0的实数，例如：.
4.零次型 等号右边是自变量的零次幂或负整数次幂，自变量的取值范围是使幂的底数不为0的实数，例如：
.
1.求下列函数的自变量的取值范围.
（1）
（2）
解：（1）函数式子无特殊情况，自变量 x 的取值范围是全体实数.
（2）函数式子含有分母，则分母不能为 0，自变量 x 的取值范围是 x≠0.
跟踪训练
新知探究
（3）
（4）.
解：（3）函数式子含有二次根式，则被开方数 ≥ 0，
x - 4 ≥ 0，解得 x ≥ 4.
（4）函数式子含有分母和二次根式，则分母不能为 0并且被开方数 ≥ 0，自变量x的取值范围是 x > -1.
2.希望高中今有1 000本图书借给学生阅读，每个学生可以借阅 5 本书，写出剩余的图书本数 y 和借阅学生人数 x 之间的函数关系式，并求出自变量的取值范围.
分析：每个学生可以借书5本，则x个学生可以借书5x本，根据剩余图书数量=图书的总数量-借出的图书总量,列出函数关系式.
解：每个学生可以借书 5 本, 则 x 个学生可以借书5x 本.
则y与x之间的函数关系式为 y=1 000-5x.
自变量的取值范围为：0≤x≤200，且 x 取整数.
1.函数解析式 用关于自变量的数学式子表示函数与自变量之间的关系，是描述函数的常用方法，这种式子叫做函数的解析式.
知识点03：函数解析式与函数值
新知探究
注意：通常函数解析式等号右边的代数式中的变量是自变量，等号左边的变量是因变量.
找
认真审题，根据题意找出各个量之间的数量关系.
根据数量关系写出含有两个变量的等式.
写
变
将等式变形为用含自变量的式子表示因变量的形式.
确定函数解析式的步骤
2.函数值 对于自变量 x 在取值范围内的某个确定的值 a，函数 y 所对应的值为 b，即当 x=a 时，y=b，则 b叫做当自变量的值为 a 时的函数值.
注意：当自变量的值确定时，函数值是唯一确定的；当函数值确定时，求相应的自变量的值，就是解方程，对应的自变量的值可以不止一个.
(1)写出表示 y 与 x 的函数关系的式子；
解: (1)行驶路程 x 是自变量，油箱中的油量 y 是 x 的函数，它们的关系为 y= 50-0.1x.
例 汽车油箱中有汽油 50 L. 如果不再加油，那么油箱中的油量 y (单位：L)随行驶路程 x(单位：km)的增加而减少，耗油量为 0.1 L/km.
(2)指出自变量 x 的取值范围；
解: (2) 仅从式子 y=50-0.1x 看，x 可以取任意实数. 但考虑到 x 代表的实际意义，因此 x 不能取负数.
行驶中的耗油量为 0.lx，它不能超过油箱中原有汽油量，即 0.l x ≤50，
因此，自变量 x 的取值范围是 0≤ x ≤500.
(3)汽车行驶 200 km 时，油箱中还有多少汽油？
解: (3)汽车行驶 200 km 时，油箱中的汽油量是函数 y=50-0.lx 在 x=200 时的函数值.
将 x=200 代入 y=50-0.1x，得 y=50-0.1×200=30.
汽车行驶 200 km 时，油箱中还有 30 L 汽油.
1.拖拉机开始工作时，油箱中有油 36 L，如果每小时耗油4 L，那么油箱中剩余油量 y L 与工作时间 x h 之间的函数解析式是 ，自变量 x 的取值范围是 ，当 x=4 时，函数值 y= .
跟踪训练
新知探究
y = 36- 4x
0 ≤ x ≤ 9
20
分析：x h的耗油量为4x，则
剩余油量=总油量-已经消耗的油量,即y = 36- 4x .
由题意知，0≤ 36- 4x ≤36.
当x=4 时， y= 36-4 ×4=20.
2.甲乙两地相距 150 公里，张三驾驶私家车从甲地开往乙地，并且以每小时 45 公里的速度匀速行驶，t 小时后张三距离乙地 s 公里，请写出 s 和 t 的函数解析式，并计算 3 小时后，s 的值为多少？
解：每小时行驶 45 公里，t 小时行驶了45t 公里.
函数解析式为 s = 150 - 45t(0≤t≤).
当 t =3 时，s =150-453 =15.
1. 在函数 中，自变量 x 的取值范围是（ ）.
A. x<4 B. x≥4 且 x≠-3 C. x>4 D. x≤4 且 x≠-3
解：由题意得 解得 x≤4 且 x≠-3.
D
随堂练习
2. 油箱中有油 50 L，油从管道中均匀流出，2.5小时能够全部流完. 油箱中剩余的油量 y 与流出时间 t 之间的函数关系式是什么？自变量的取值范围是多少？
分析：先求出每小时流出的油量，再根据剩余的油量 = 总油量 - 流出的油量,列出函数关系式.
解: 50 L的油2.5小时能够全部流完，则每小时流出油量为20 L,
则 y 与 t 之间的函数关系式为 y=50-20t,
自变量为 t，取值范围为0≤ t ≤2.5
①t从0开始
②最多流2.5小时
分析：根据等腰三角形的周长=腰长+腰长+底边长,列出函数关系式; 自变量是腰长, 取值范围要有实际意义.
3.等腰三角形的周长为15，底边长为 y，腰长为 x.
（1）写出 y 关于 x 的函数关系式；
（2）求出 x 的取值范围.
解：（1） ∵三角形的腰长为 x，底边长为 y.
∴三角形的周长=x+x+y，即15=2x+y，解得 y=15-2x.
（2）∵ x，y 是三角形的边长，∴ x>0，y>0，2x>y，∴ 自变量 x 的取值范围是 4.判断下列变量之间是否具有函数关系，并说明理由.
（1）y=x;（2）;
（3）;（4）
解：（1）（3）不具有函数关系.例如当 x=1 时，
（1）中 y =1和 y = -1，（3）中 y = 和 y =-.
（2）（4）符合函数定义,具有函数关系.
5.指出下列问题中的变量，并写出变量之间的关系.
（1）正方形的面积 S 与边长 a 之间的变化关系；
（2）圆的周长 C 与半径 r 之间的变化关系.
（3）高铁的速度为 250 km/h，则路程 S km与时间 t h之间的变化关系.
解：变量：S，a；.
解：变量：C，r；C= 2 r.
解：变量：S，t；S=250 t.
6.判断下列变量之间的关系是不是函数关系.
（1）矩形的长一定，宽与周长之间的关系；
（2）圆的面积与半径之间的关系.
解：是函数关系. 矩形的长一定时，其周长随着宽的长的变化而变化，并且给定的宽的值都有确定的周长值与之对应.
解：是函数关系. 圆的面积随着半径长度的变化而变化，并且给定的半径的值都有确定的面积值与之对应.
解：不是函数关系. 等腰三角形的高不确定，所以面积的变化不由底边的变化唯一决定.
（3）等腰三角形底边长与面积之间的关系.
7.某火力发电厂共储存煤1 000吨，每天发电用煤50吨，设发电天数为 x，该发电厂开始发电后，储存煤量为 y 吨. 请写出 y 与 x 之间的函数解析式及自变量 x 的取值范围.
分析：运用等量关系“储存煤量=总储存煤量-用煤量”列函数解析式.
解：由题意知，发电 x 天用煤量为 50x 吨，发电前共
储存煤1 000吨.
所以 y 与 x之间的函数解析式为 y=-50x+1000(0≤x≤20).
易错警示：
对自变量的的取值范围考虑不周致错
自变量的取值范围不仅要使所列函数解析式有意义，还要使实际问题有意义.本题中x表示天数，其值应为非负数，由题意可知1 000吨煤最多用20天，即x的最大值为20，所以x的取值范 围为0≤x≤20.
8.小明带着 100 元去超市买汽水，已知一瓶汽水为 5 元，那么小明剩余的钱数 y 与购买汽水的数量 x 之间的函数解析式是什么？自变量的取值范围是多少？
分析：根据“剩余的钱数 = 总钱数 - 购买汽水花费的钱数”列出函数解析式.
解：一瓶汽水 5 元，则购买 x 瓶汽水花费 5x 元.
函数解析式为 y = 100 - 5x.
根据实际问题有意义，得自变量 x 的取值范围是 0 ≤ x ≤ 20.
9.一盒中性笔有 10 支，价格为 15 元. 请写出购买中性笔支数 x 与花费的总钱数 y 之间的关系式.
解：根据题意，得 10 支中性笔的价格为 15 元，则 1 支中性笔的价格为 1.5 元.
花费的总钱数 = 单价购买中性笔数量，即 y =1.5x.
函数
概念
判断
方法
在一个变化过程中，如果有两个变量 x 与 y，并且对于 x 的每一个确定的值，y 都有唯一确定的值与其相对应.
1.看是否在一个变化过程中；
2.看是否存在两个变量；
3.看每当变量取定一个值时，另外一个变量是否都有唯一确定的值与其相对应.
课堂小结
函数自变量的取值范围
概念
不同类型函数自变量取值范围的确定
使函数关系式有意义的自变量取值的全体叫做自变量的取值范围.
①整式型（全体实数）；
②分式型（使分母不为0的实数）；③根式型（使根号下的式子的值大于或等于0的实数）；
④零次型（使幂的底数不为0的实数）
课堂小结
解析式
函数值
用关于自变量的数学式子表示函数与自变量之间的关系，是描述函数的常用方法，这种式子叫做函数的解析式.
对于自变量x在取值范围内的某个确定的值a，函数y所对应的值为b，b即为函数值.
函数解析式和函数值
课堂小结
1.观察下表中的数量关系，说法正确的是（ ）.
A. x是y的函数 B. y是x的函数
C. y不是x的函数 D. x是y的函数 ，y也是x的函数
x 1 2 3 4 5 6 7
y/元 1 1 2 2 3 3 3
（ x表示乘坐公共汽车的站数，y表示应付的票价.）
B
解析：对于每一个站数 x，都有唯一的票价 y . 但是对于每一个票价 y，有不同的公共汽车的站数 x 对应.
拓展提升
2.下列关系式中，b 不是 a 的函数的是（ ）.
A. b=2a B. b=5a
C. D.
D
解析：选项D中，对于一个确定的a ，不都是有唯一
确定的b与之对应.
3.如图所示的图象中,表示y是x的函数的个数是（ ）.
A. 1 B. 2 C. 3 D. 4
B
技巧点拨：作辅助线识别函数关系：过x轴上任意一点作x轴的垂线，若与图象有两个或两个以上的交点，则该图象不能表示函数关系.
解析：观察图象（1）（2）中，对于任意一个 x 的值， y 都有唯一确定的值与之对应，所以满足题意；而图象（3）（4）中，对可取范围内 x 的值， y与之对应的值不都是唯一的，所以不满足题意.
4.下列函数中，自变量的取值范围选取错误的是（ ）.
A. 中，x 取全体实数
B. 中，x 取 x≠-3 的全体实数
C. 中，x 取 x≥2 的全体实数
D. 中，x 取 x≥1 的全体实数
D
分母不能为零
5.某书定价 30 元，如果一次购书 20 本以上，超出 20本的部分打八折，请写出付款金额 y（单位：元）与购书数量 x（单位：本）之间的函数关系式并写出自变量的取值范围.
分析：①购书数量不超过 20 本， y = 30 x.
②购书数量超过 20 本， 20 本按照 30 元的单价，总共需要600 元；超过的数量为（x-20），超过部分的单价为 24 元，所以总价格为 y = 600 + 24(x-20).
6.某书定价 30 元，如果一次购书 20 本以上，超出 20本的部分打八折，请写出付款金额 y（单位：元）与购书数量 x（单位：本）之间的函数关系式并写出自变量的取值范围.
易错提醒：
此题要分情况讨论：
①购书数量不超过 20 本；
②购书数量超过 20 本.
解：
30x（0 ≤ x≤20）,
600+24（x-20）(x>20) .
y =
7.李老师带着学生去科技馆参观，李老师的票价为 40 元，每个学生的票价为 30 元，试写出李老师应带门票的总费用 y（元）和学生人数 x 之间的函数解析式.
分析：李老师去科技馆参观也是需要门票的，同时学生花费的门票总价=单价学生人数.
解：因为每个学生的票价为 30 元，所以 x 个学生的门票总费用是 30x.李老师应带的门票的总费用=李老师的门票费用 + 所有学生的门票总费用，即 y = 40+30x.
8.本市出租车的收费标准如下：乘坐公里数不超过 3 公里的，一律按照 10 元收费；超过 3 公里的部分，每公里加收 3 元. 设乘坐公里数为 x 公里，相对应的收费为 y 元.
（1）请分别写出 x>3 和 0分析：①当 0②当 x>3 时，超过 3 公里的部分，每公里加收 3元，则 y =10+3（x-3）=3x+1.
解：y =
10 (03x+1 (x>3).
9.本市出租车的收费标准如下：乘坐公里数不超过 3 公里的，一律按照 10 元收费；超过 3 公里的部分，每公里加收 3 元. 设乘坐公里数为 x 公里（x 为整数），相对应的收费为 y 元.
（2）直接写出当 x=2 和 x=5 时的函数值.
解：因为0< 2 < 3 ，所以当 x=3时，收费为 10 元.
因为 5 >3 ，所以当 x=5 时，收费为 16 元.
谢谢
21世纪教育网（www.21cnjy.com)
中小学教育资源网站
兼职招聘：
https://www.21cnjy.com/recruitment/home/admin