全等三角形复习1[上学期]
文档属性
| 名称 | 全等三角形复习1[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 142.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-16 23:09:00 | ||
图片预览


文档简介
课件18张PPT。
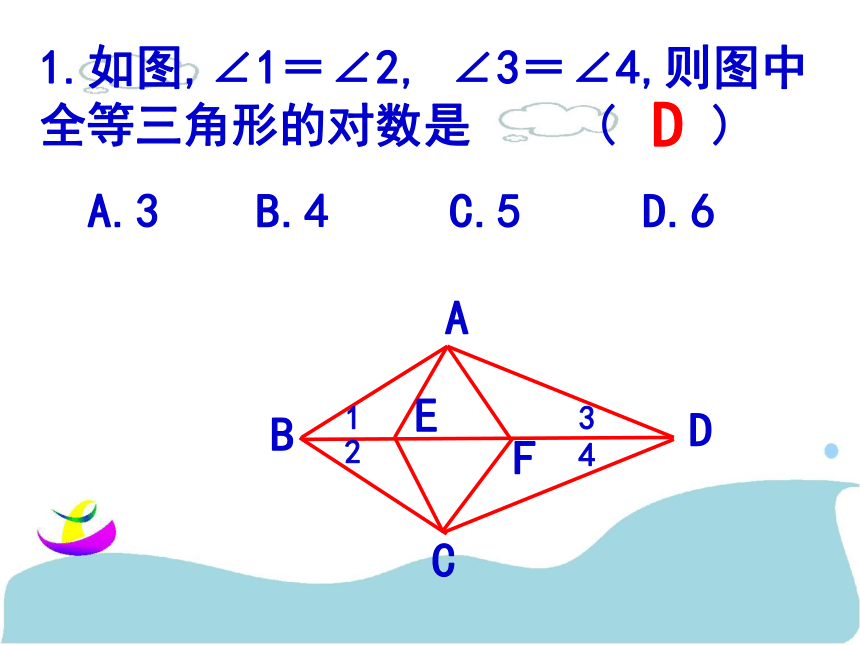
全等三角形复习 1全等图形:全等三角形:基础知识复习能够完全重合的两个图形能够完全重合的两个三角形探索三角形全等的条件SSS SAS ASA AAS HLSSS SAS(两边夹角) ASA (两角夹边) AAS1、两个三角形全等的条件:2、两个直角三角形全等的条件:至少有一个条件是边1.如图,∠1=∠2, ∠3=∠4,则图中全等三角形的对数是 ( )
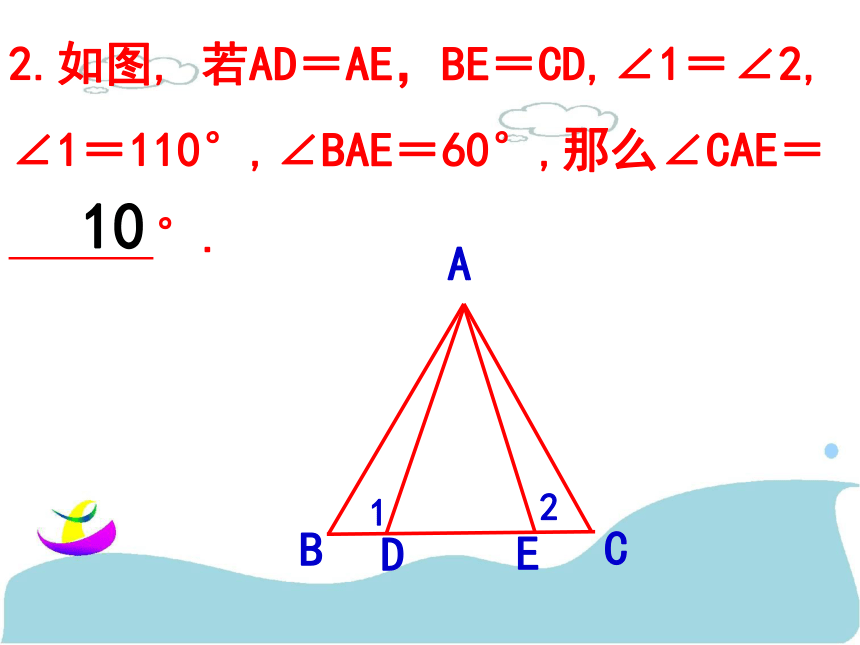
A.3 B.4 C.5 D.6D2.如图, 若AD=AE,BE=CD,∠1=∠2,
∠1=110°,∠BAE=60°,那么∠CAE=
°.
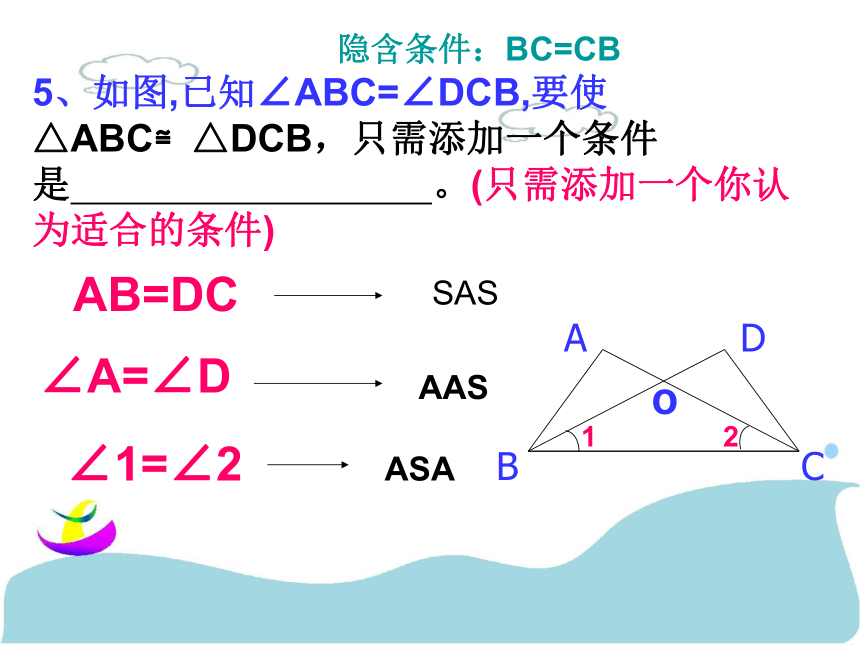
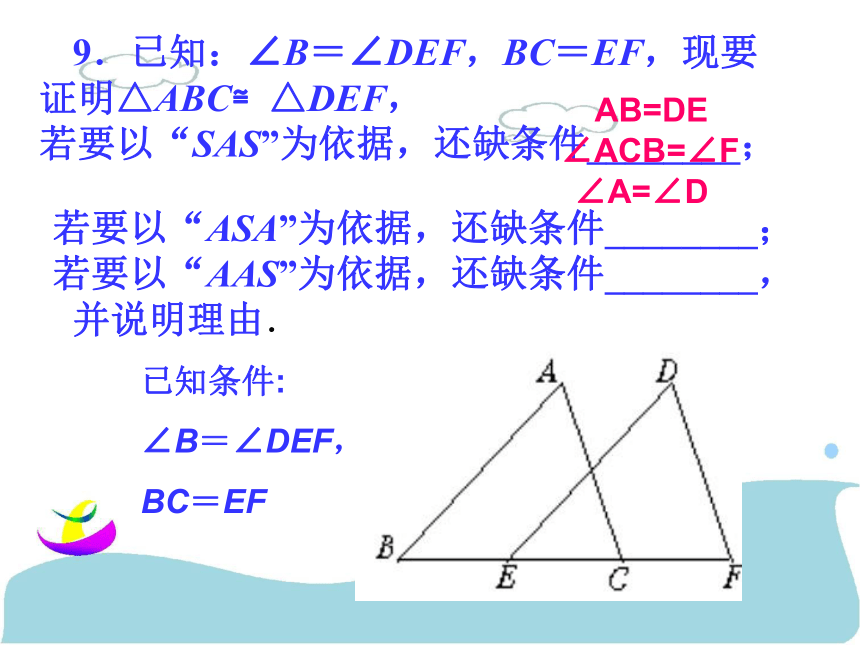
105、如图,已知∠ABC=∠DCB,要使△ABC≌△DCB,只需添加一个条件是 。(只需添加一个你认为适合的条件)AB=DC∠A=∠D∠1=∠212隐含条件:BC=CBSASAASASA 9.已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,
若要以“SAS”为依据,还缺条件________;
若要以“ASA”为依据,还缺条件________;
若要以“AAS”为依据,还缺条件________,
并说明理由.AB=DE∠ACB=∠F∠A=∠D已知条件:
∠B=∠DEF,
BC=EF3.在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,那么∠ABC= °.454. 如图,M是AB的中点 ,∠1 = ∠2 ,MC=MD.试说明ΔACM ≌ ΔBDM证明: ∵ M是AB的中点 (已知)
∴ MA=MB(中点定义)
∵ ∠1 = ∠2 (已知)
MC=MD(已知)
∴ΔACM ≌ ΔBDM (SAS)5.已知:如图,∠1=∠2,∠B=∠D。
求证:△ABC≌△ADC
在△ABC与△ADC中
∵ ∠1=∠2(已知)
∠B=∠D(已知)
AC=AC(公共边)
∴ △ABC≌△ADC(AAS)6.如图, AC⊥CB, BD⊥BC, AB=DC, 判断AB与CD是否平行?为什么?答: AB∥CD .
∵AC⊥CB,BD⊥BC(已知) ∴△ACB与△DBC是直角三角形∵AB=DC(已知)
BC=CB(公共边) ∴△ACB≌△DBC (HL)
∴∠1=∠2(全等三角形对应角相等)
∴ AB∥CD(内错角相等,两直线平行)7、如图,已知AB=AC,BD=CE。
求证:△ABE≌△ACD。
在△ABE与△ACD中
∵ AB=AC(已知)
AD=AE(已证)
∠A=∠A(公共角)
∴ △ABE≌△ACD(SAS)证明:∵ AB=AC,BD=CE(已知)
∴AD=AE(等式性质)
8、已知:AD⊥BC,D为垂足,AD=BD,DC=DE,那么,∠C=∠BED。为什么?ABCDE分析:要∠C=∠BED,只需证⊿ADC≌⊿BDE结合已知考虑“SAS”证之证明:∵AD⊥BC于D,∴∠ADC=∠BDE=90°在⊿ADC和⊿BDE 中AD=BD∠ADC=∠BDEDC=DE⊿ADC≌⊿BDE∠C=∠BED操作思考与10.如图,将长方形ABCD沿直线BD折叠一次 (折痕与折叠后得到的图形用虚线表示),请将得到的所有全等三角形(包括实线、虚线在内), 用符号表示出来.并说明理由.BCDAEF在△ABC中,AD平分∠BAC,CE⊥AD,垂足是G,EF∥BC.说明:EC平分∠FED. 探究:探究:
已知:ΔABC和ΔBDE是等边三角形, 点D在AE的延长线上。
求证:BD + DC = AD
分析:∵AD = AE + ED
∴只需证:BD + DC = AE + ED
∵BD = ED
∴只需证DC = AE即可。
●通过本节课的学习,你有哪些收获? ●本节课你还有哪些疑问? ●通过本节课的学习,你有哪些收获? ●本节课你还有哪些疑问?
全等三角形复习 1全等图形:全等三角形:基础知识复习能够完全重合的两个图形能够完全重合的两个三角形探索三角形全等的条件SSS SAS ASA AAS HLSSS SAS(两边夹角) ASA (两角夹边) AAS1、两个三角形全等的条件:2、两个直角三角形全等的条件:至少有一个条件是边1.如图,∠1=∠2, ∠3=∠4,则图中全等三角形的对数是 ( )
A.3 B.4 C.5 D.6D2.如图, 若AD=AE,BE=CD,∠1=∠2,
∠1=110°,∠BAE=60°,那么∠CAE=
°.
105、如图,已知∠ABC=∠DCB,要使△ABC≌△DCB,只需添加一个条件是 。(只需添加一个你认为适合的条件)AB=DC∠A=∠D∠1=∠212隐含条件:BC=CBSASAASASA 9.已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,
若要以“SAS”为依据,还缺条件________;
若要以“ASA”为依据,还缺条件________;
若要以“AAS”为依据,还缺条件________,
并说明理由.AB=DE∠ACB=∠F∠A=∠D已知条件:
∠B=∠DEF,
BC=EF3.在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,那么∠ABC= °.454. 如图,M是AB的中点 ,∠1 = ∠2 ,MC=MD.试说明ΔACM ≌ ΔBDM证明: ∵ M是AB的中点 (已知)
∴ MA=MB(中点定义)
∵ ∠1 = ∠2 (已知)
MC=MD(已知)
∴ΔACM ≌ ΔBDM (SAS)5.已知:如图,∠1=∠2,∠B=∠D。
求证:△ABC≌△ADC
在△ABC与△ADC中
∵ ∠1=∠2(已知)
∠B=∠D(已知)
AC=AC(公共边)
∴ △ABC≌△ADC(AAS)6.如图, AC⊥CB, BD⊥BC, AB=DC, 判断AB与CD是否平行?为什么?答: AB∥CD .
∵AC⊥CB,BD⊥BC(已知) ∴△ACB与△DBC是直角三角形∵AB=DC(已知)
BC=CB(公共边) ∴△ACB≌△DBC (HL)
∴∠1=∠2(全等三角形对应角相等)
∴ AB∥CD(内错角相等,两直线平行)7、如图,已知AB=AC,BD=CE。
求证:△ABE≌△ACD。
在△ABE与△ACD中
∵ AB=AC(已知)
AD=AE(已证)
∠A=∠A(公共角)
∴ △ABE≌△ACD(SAS)证明:∵ AB=AC,BD=CE(已知)
∴AD=AE(等式性质)
8、已知:AD⊥BC,D为垂足,AD=BD,DC=DE,那么,∠C=∠BED。为什么?ABCDE分析:要∠C=∠BED,只需证⊿ADC≌⊿BDE结合已知考虑“SAS”证之证明:∵AD⊥BC于D,∴∠ADC=∠BDE=90°在⊿ADC和⊿BDE 中AD=BD∠ADC=∠BDEDC=DE⊿ADC≌⊿BDE∠C=∠BED操作思考与10.如图,将长方形ABCD沿直线BD折叠一次 (折痕与折叠后得到的图形用虚线表示),请将得到的所有全等三角形(包括实线、虚线在内), 用符号表示出来.并说明理由.BCDAEF在△ABC中,AD平分∠BAC,CE⊥AD,垂足是G,EF∥BC.说明:EC平分∠FED. 探究:探究:
已知:ΔABC和ΔBDE是等边三角形, 点D在AE的延长线上。
求证:BD + DC = AD
分析:∵AD = AE + ED
∴只需证:BD + DC = AE + ED
∵BD = ED
∴只需证DC = AE即可。
●通过本节课的学习,你有哪些收获? ●本节课你还有哪些疑问? ●通过本节课的学习,你有哪些收获? ●本节课你还有哪些疑问?
