全等三角形复习2[上学期]
文档属性
| 名称 | 全等三角形复习2[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 897.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-17 21:07:00 | ||
图片预览



文档简介
课件20张PPT。
全等三角形复习 2教学目标:
1:掌握三角形的基本要素及基本性质、全等。
2:灵活运用三角形的基本性质和全等条件。
重点:
掌握三角形全等的条件。
难点:
在直观认识和操作活动的基础上,运用自己的语言表达,发展推理能力。1、三角形的边角关系(1)任意两边之和大于第三边,任意两边之差小于第三边(2)三角形的内角和等于1802、三角形分类三角形按角分为锐角三角形
直角三角形
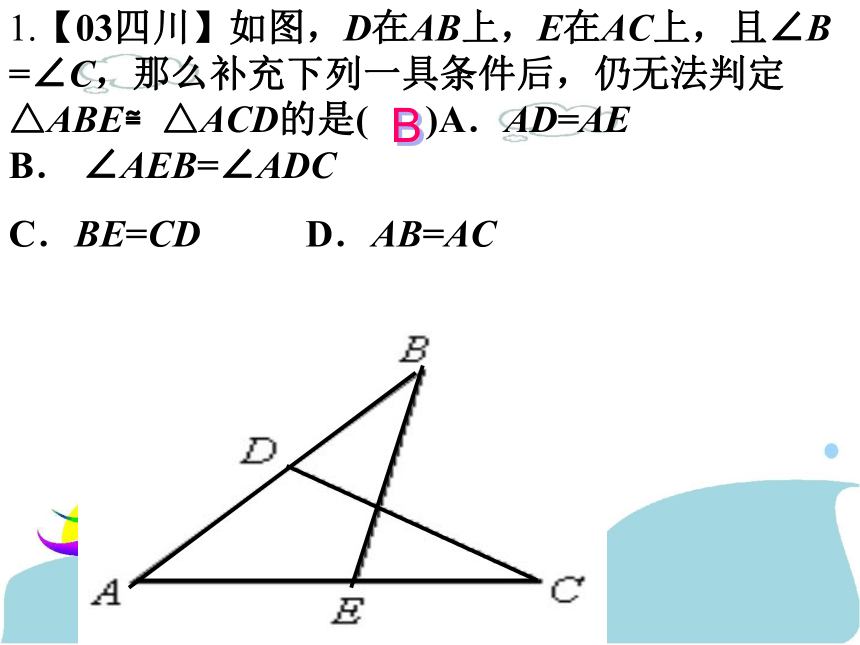
钝角三角形3、三角形全等的条件(1)一般三角形:SAS、ASA、AAS、SSS1.【03四川】如图,D在AB上,E在AC上,且∠B =∠C,那么补充下列一具条件后,仍无法判定△ABE≌△ACD的是( )A.AD=AE B. ∠AEB=∠ADC
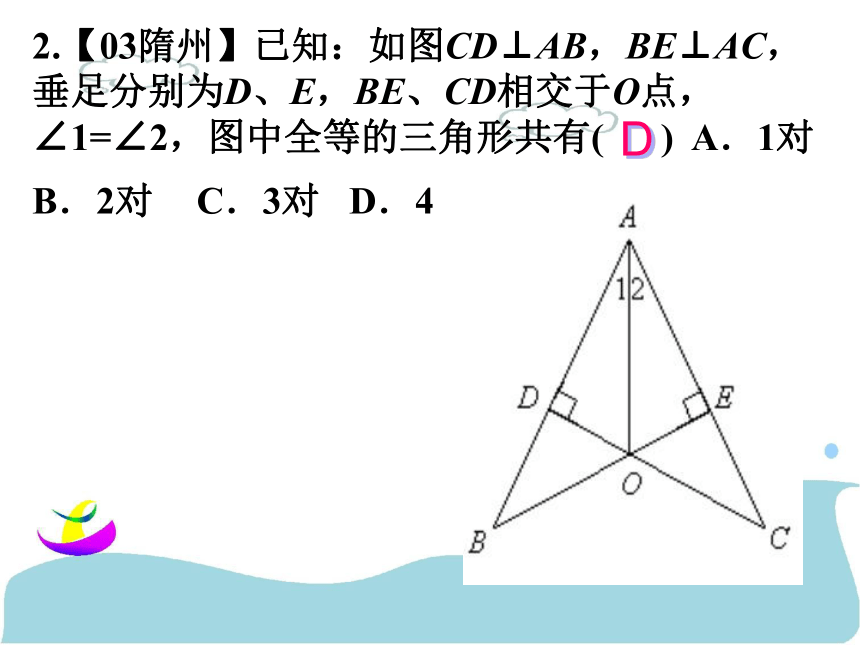
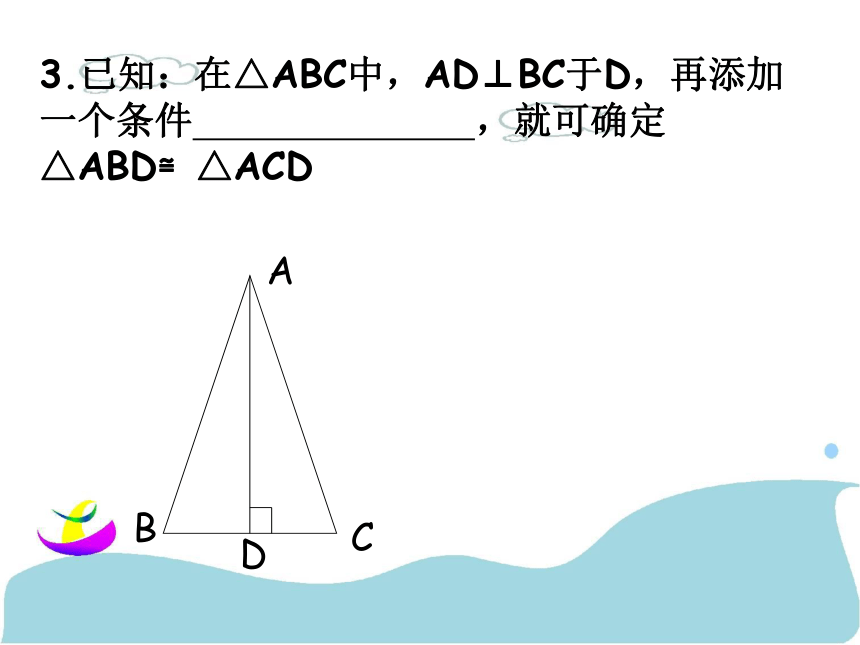
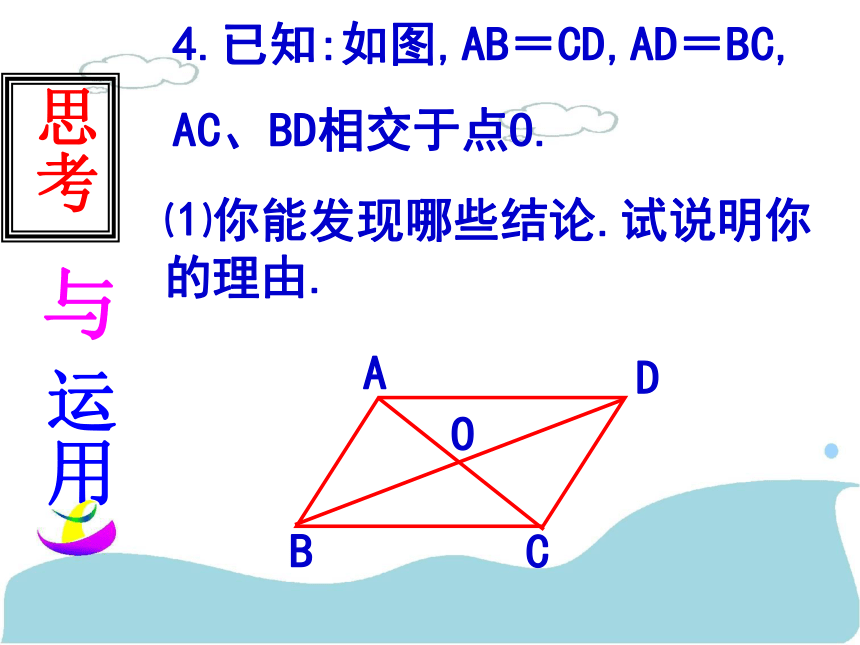
C.BE=CD D.AB=ACB2.【03隋州】已知:如图CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2,图中全等的三角形共有( ) A.1对 B.2对 C.3对 D.4 D3.已知:在△ABC中,AD⊥BC于D,再添加一个条件 ,就可确定△ABD≌△ACD运用思考与4.已知:如图,AB=CD,AD=BC,
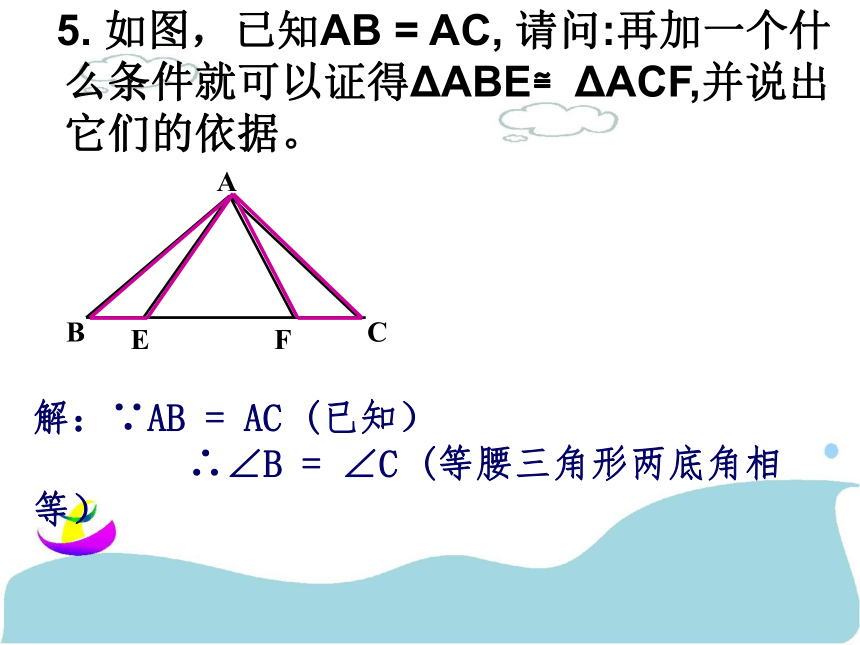
AC、BD相交于点O.⑴你能发现哪些结论.试说明你的理由. 5. 如图,已知AB = AC, 请问:再加一个什么条件就可以证得ΔABE≌ΔACF,并说出它们的依据。
解:∵AB = AC (已知)
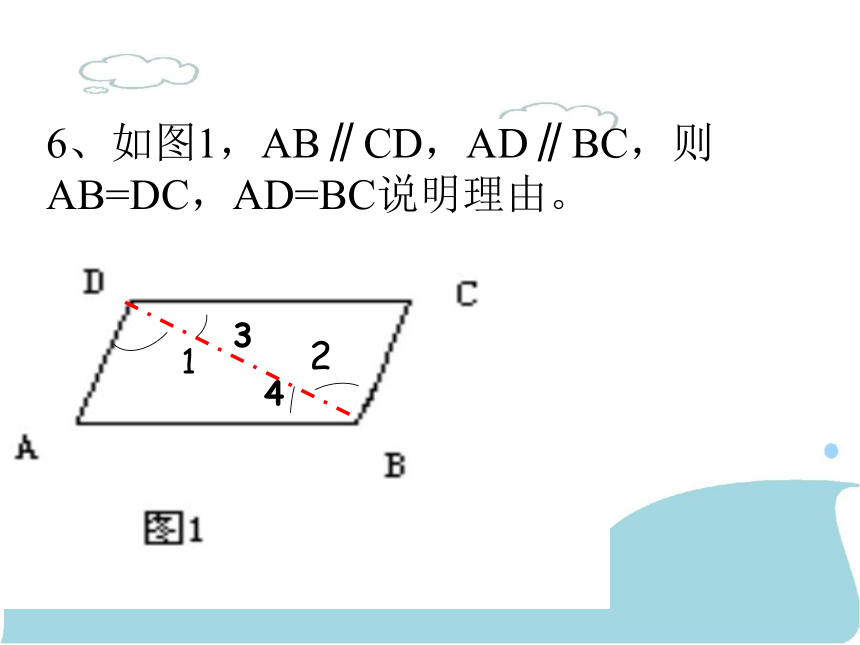
∴∠B = ∠C (等腰三角形两底角相等)6、如图1,AB∥CD,AD∥BC,则AB=DC,AD=BC说明理由。 7.如图,在四边形ABCD中,已知
AB=AD,CD=CB,则图形中哪些角
必定相等?请说明理由。解: ∴∠ADC=∠ABC在△ABC与△ADC中
∵ AB=AD,(已知)
CD=CB(已知)
AC=AC(公共边)
∴ △ABC≌△ADC(SSS)
∴∠ADC=∠ABC(≌△对应角相等)连结AC
8.如图,AB=DC,AC=DB,
你能说明图中∠1=∠2的理由吗?9.如图,AB=AC,∠ B=∠C,
点D、E在BC上,且BD=CE,
那么图中又哪些三角形全等?请选择
其中一对说明理由。9.如图,AB=CD,AD=BC,O为AC
中点,过O点的直线分别交AD、BC
于M、N,你能说明∠1=∠2吗?拓展练习1.①.已知如图1 AB=CD AD=BC,求证:∠A= ∠C②.已知如图2 AB=DC AD=CB,F为AD的中点连结BF并延长交CD的延长线于E , 求证:DE= DC③.已知如图3 AB=DC AD=CB,延长AB于F,延长CD于E使BF=DE 。
求证:BE=DF2. 已知:如图,在平形四边形ABCD中,
E、F是对角线AC上的两点,且AE=CF。
??? 求证:DE=BF
???
北京丰台3.如图,在△ABE和△ACD中,给出以下四个论断:⑴ AB = AC; ⑵ AD = AE; ⑶ AD⊥DC, AE⊥BE; ⑷ AM = AN .能否以其中三个论断为条件,另一个论断为结论,使之组成一个正确的推断?说明理由.【99江西】已知,如图,BC=BD,∠C=∠D,
求证:AC=AD.
4.已知:ΔABC和ΔBDE是等边三角形, 点D在AE的延长线上。
求证:BD + DC = AD
分析:∵AD = AE + ED
∴只需证:BD + DC = AE + ED
∵BD = ED
∴只需证DC = AE即可。
思考题 .如图,D为等边△ABC外一点,且BD=CD,∠BDC= 120°,M、N分别 在AB、AC上,若BM+CN=MN,
求证: ∠MDN=60°。 ●通过本节课的学习,你有哪些收获? ●本节课你还有哪些疑问?
全等三角形复习 2教学目标:
1:掌握三角形的基本要素及基本性质、全等。
2:灵活运用三角形的基本性质和全等条件。
重点:
掌握三角形全等的条件。
难点:
在直观认识和操作活动的基础上,运用自己的语言表达,发展推理能力。1、三角形的边角关系(1)任意两边之和大于第三边,任意两边之差小于第三边(2)三角形的内角和等于1802、三角形分类三角形按角分为锐角三角形
直角三角形
钝角三角形3、三角形全等的条件(1)一般三角形:SAS、ASA、AAS、SSS1.【03四川】如图,D在AB上,E在AC上,且∠B =∠C,那么补充下列一具条件后,仍无法判定△ABE≌△ACD的是( )A.AD=AE B. ∠AEB=∠ADC
C.BE=CD D.AB=ACB2.【03隋州】已知:如图CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2,图中全等的三角形共有( ) A.1对 B.2对 C.3对 D.4 D3.已知:在△ABC中,AD⊥BC于D,再添加一个条件 ,就可确定△ABD≌△ACD运用思考与4.已知:如图,AB=CD,AD=BC,
AC、BD相交于点O.⑴你能发现哪些结论.试说明你的理由. 5. 如图,已知AB = AC, 请问:再加一个什么条件就可以证得ΔABE≌ΔACF,并说出它们的依据。
解:∵AB = AC (已知)
∴∠B = ∠C (等腰三角形两底角相等)6、如图1,AB∥CD,AD∥BC,则AB=DC,AD=BC说明理由。 7.如图,在四边形ABCD中,已知
AB=AD,CD=CB,则图形中哪些角
必定相等?请说明理由。解: ∴∠ADC=∠ABC在△ABC与△ADC中
∵ AB=AD,(已知)
CD=CB(已知)
AC=AC(公共边)
∴ △ABC≌△ADC(SSS)
∴∠ADC=∠ABC(≌△对应角相等)连结AC
8.如图,AB=DC,AC=DB,
你能说明图中∠1=∠2的理由吗?9.如图,AB=AC,∠ B=∠C,
点D、E在BC上,且BD=CE,
那么图中又哪些三角形全等?请选择
其中一对说明理由。9.如图,AB=CD,AD=BC,O为AC
中点,过O点的直线分别交AD、BC
于M、N,你能说明∠1=∠2吗?拓展练习1.①.已知如图1 AB=CD AD=BC,求证:∠A= ∠C②.已知如图2 AB=DC AD=CB,F为AD的中点连结BF并延长交CD的延长线于E , 求证:DE= DC③.已知如图3 AB=DC AD=CB,延长AB于F,延长CD于E使BF=DE 。
求证:BE=DF2. 已知:如图,在平形四边形ABCD中,
E、F是对角线AC上的两点,且AE=CF。
??? 求证:DE=BF
???
北京丰台3.如图,在△ABE和△ACD中,给出以下四个论断:⑴ AB = AC; ⑵ AD = AE; ⑶ AD⊥DC, AE⊥BE; ⑷ AM = AN .能否以其中三个论断为条件,另一个论断为结论,使之组成一个正确的推断?说明理由.【99江西】已知,如图,BC=BD,∠C=∠D,
求证:AC=AD.
4.已知:ΔABC和ΔBDE是等边三角形, 点D在AE的延长线上。
求证:BD + DC = AD
分析:∵AD = AE + ED
∴只需证:BD + DC = AE + ED
∵BD = ED
∴只需证DC = AE即可。
思考题 .如图,D为等边△ABC外一点,且BD=CD,∠BDC= 120°,M、N分别 在AB、AC上,若BM+CN=MN,
求证: ∠MDN=60°。 ●通过本节课的学习,你有哪些收获? ●本节课你还有哪些疑问?
