全等三角形复习3[上学期]
文档属性
| 名称 | 全等三角形复习3[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 94.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-17 21:09:00 | ||
图片预览

文档简介
课件14张PPT。
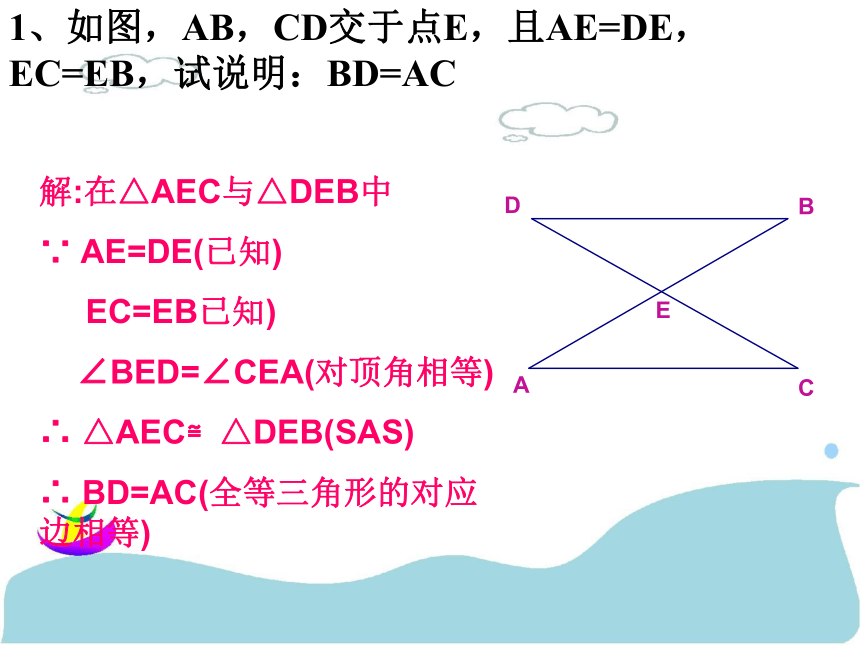
全等三角形复习 31、如图,AB,CD交于点E,且AE=DE,EC=EB,试说明:BD=AC解:在△AEC与△DEB中
∵ AE=DE(已知)
EC=EB已知)
∠BED=∠CEA(对顶角相等)
∴ △AEC≌△DEB(SAS)
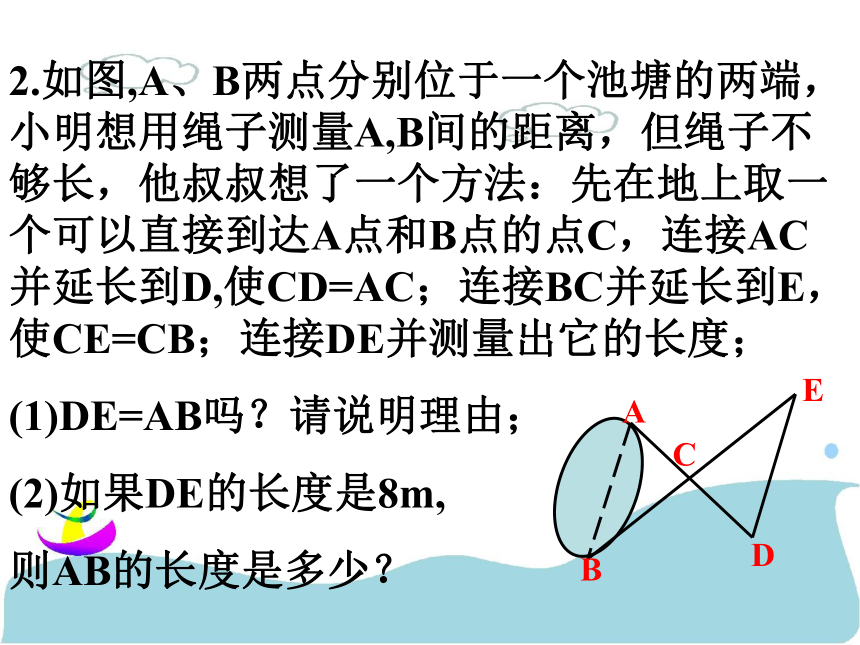
∴ BD=AC(全等三角形的对应边相等)2.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,他叔叔想了一个方法:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度;
(1)DE=AB吗?请说明理由;
(2)如果DE的长度是8m,
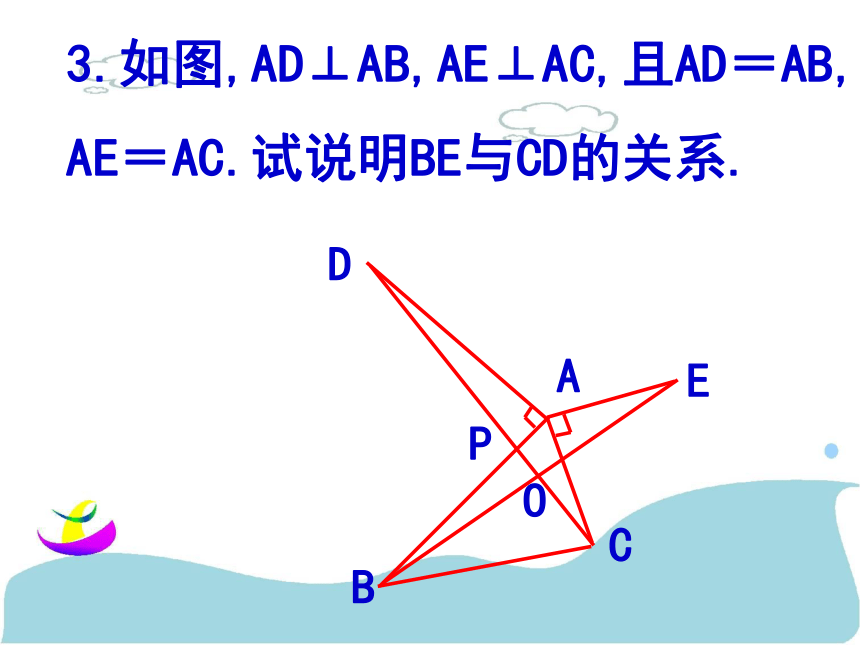
则AB的长度是多少?ACDBE3.如图,AD⊥AB,AE⊥AC,且AD=AB,
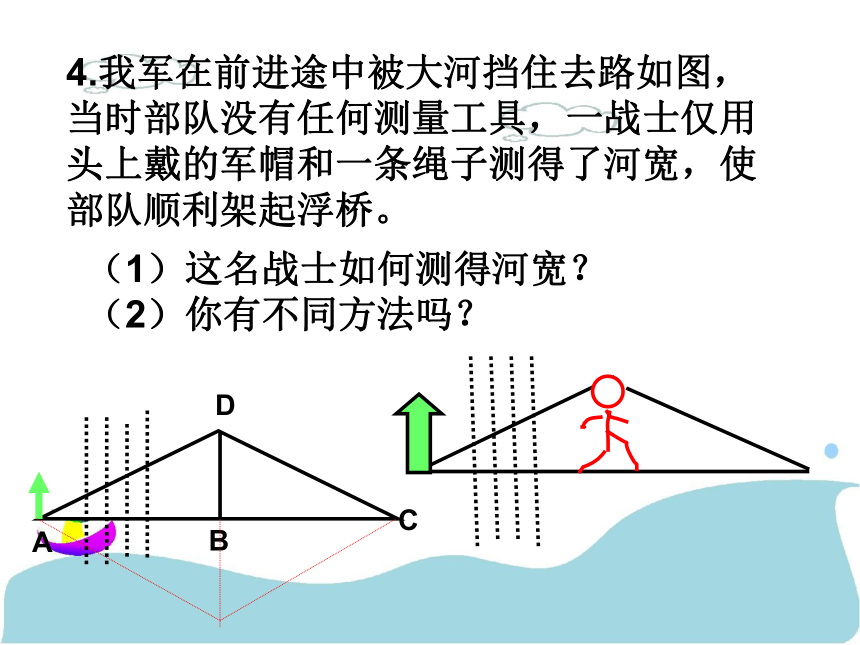
AE=AC.试说明BE与CD的关系.4.我军在前进途中被大河挡住去路如图,当时部队没有任何测量工具,一战士仅用头上戴的军帽和一条绳子测得了河宽,使部队顺利架起浮桥。(1)这名战士如何测得河宽?
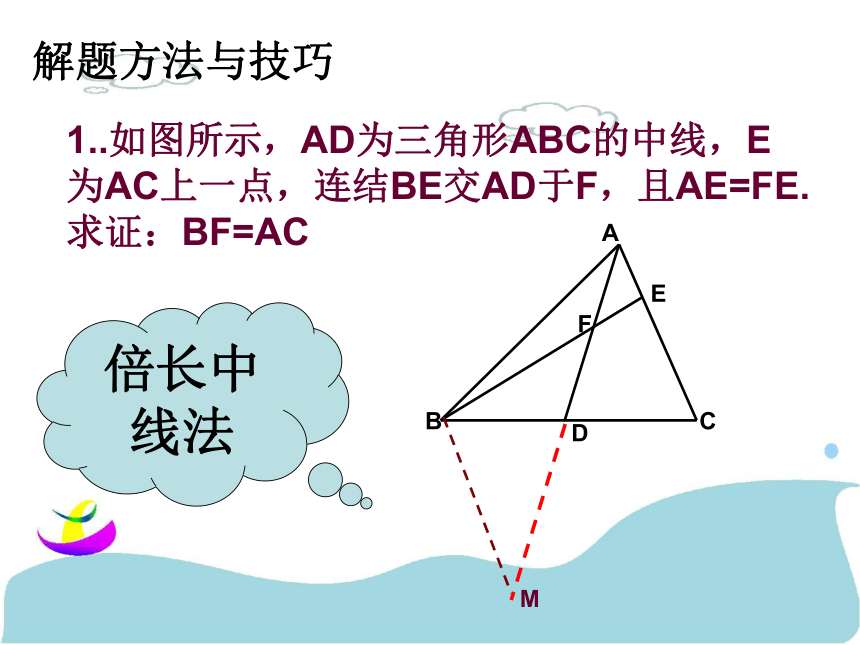
(2)你有不同方法吗?A B CD解题方法与技巧1..如图所示,AD为三角形ABC的中线,E为AC上一点,连结BE交AD于F,且AE=FE.
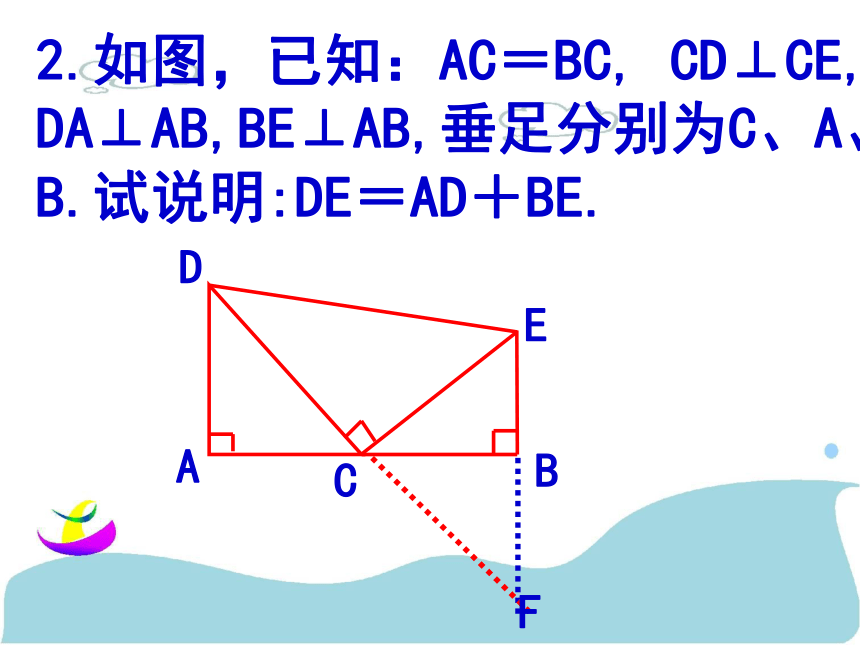
求证:BF=ACM倍长中线法2.如图,已知:AC=BC, CD⊥CE, DA⊥AB,BE⊥AB,垂足分别为C、A、B.试说明:DE=AD+BE.F3.已知,如图,在三角形ABC中,AB求证:AC=AB+BDE截长补短综合应用:1.如图是某城市部分街道示意图,AB=BC= AC,CD= CE=DE,A、 B、C、D、E、F 、G、H为“中巴”停靠点,“中巴甲”从A站出发,按照A→H→G→D→E→C→F的顺序到达F站,“中巴乙”从B站出发,沿F→H→E→D→C→G 的顺序到达G站,若甲、乙分别从A、B站出发,在各站停的时间、车速均一样,试问哪一辆先到达指定站,为什么?ACDBEFHG 思路:看图可知:⊿ACD≌⊿BEC,∴AD=BE,ED=DE=EC=DC,
又⊿AGC≌⊿BFC,∴GC=FC,∴他们是同时到达。甲乙1.已知,如图,AB=14,AC=10,AD平分∠BAC,CE⊥AD于点E,M为BC边中点
求:线段ME的长F如果有与角平分线垂直的线段时,常把它延长与角的边相交构造等腰三角形
2.如图△ABC中,AB=AC,∠A=108°,BD平分∠ABC交AC于D,
求证:BC=AB+CD。 C 注意利用全等三角形解决实际问题的步骤:
(1)先明确实际问题应用哪些几何知识解决。
(2)根据实际抽象出几何图形。
(3)结合图形和题意分析已知条件。
(4)找到解决问题的途径并表达清楚。 ●通过本节课的学习,你有哪些收获? ●本节课你还有哪些疑问?
全等三角形复习 31、如图,AB,CD交于点E,且AE=DE,EC=EB,试说明:BD=AC解:在△AEC与△DEB中
∵ AE=DE(已知)
EC=EB已知)
∠BED=∠CEA(对顶角相等)
∴ △AEC≌△DEB(SAS)
∴ BD=AC(全等三角形的对应边相等)2.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,他叔叔想了一个方法:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度;
(1)DE=AB吗?请说明理由;
(2)如果DE的长度是8m,
则AB的长度是多少?ACDBE3.如图,AD⊥AB,AE⊥AC,且AD=AB,
AE=AC.试说明BE与CD的关系.4.我军在前进途中被大河挡住去路如图,当时部队没有任何测量工具,一战士仅用头上戴的军帽和一条绳子测得了河宽,使部队顺利架起浮桥。(1)这名战士如何测得河宽?
(2)你有不同方法吗?A B CD解题方法与技巧1..如图所示,AD为三角形ABC的中线,E为AC上一点,连结BE交AD于F,且AE=FE.
求证:BF=ACM倍长中线法2.如图,已知:AC=BC, CD⊥CE, DA⊥AB,BE⊥AB,垂足分别为C、A、B.试说明:DE=AD+BE.F3.已知,如图,在三角形ABC中,AB
又⊿AGC≌⊿BFC,∴GC=FC,∴他们是同时到达。甲乙1.已知,如图,AB=14,AC=10,AD平分∠BAC,CE⊥AD于点E,M为BC边中点
求:线段ME的长F如果有与角平分线垂直的线段时,常把它延长与角的边相交构造等腰三角形
2.如图△ABC中,AB=AC,∠A=108°,BD平分∠ABC交AC于D,
求证:BC=AB+CD。 C 注意利用全等三角形解决实际问题的步骤:
(1)先明确实际问题应用哪些几何知识解决。
(2)根据实际抽象出几何图形。
(3)结合图形和题意分析已知条件。
(4)找到解决问题的途径并表达清楚。 ●通过本节课的学习,你有哪些收获? ●本节课你还有哪些疑问?
