第二十三章 旋转单元测试题(含解析)
图片预览


文档简介
本章综合检测
(时间:60分钟 满分:100分)
、选择题(每小题3分,共30分)
1.(黑龙江鸡西中考)下列图形中,既是轴对称图形又是中心对称图形的个数为( )
A.1 B.2 C.3 D.4
2.如图23-12,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,在同一条直线上,那么旋转角等于( )
A.55° B.70° C.125° D.145°
3.在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到,若点B的坐标为,则点B的对应点的坐标为( )
A. B. C. D.
4.(江苏泰州中考)下列图案中,既是轴对称图形,又是中心对称图形的是( )
5.如图23-13,若正方形EFGH由正方形ABCD绕某点旋转得到,则可以作为旋转中心的是( )
A.点M或点O或点N B.点E或点O或点C
C.点E或点O或点N D.点M或点O或点C
6.图23-14是某个万花筒内部的图案,图中的小三角形均是全等的等边三角形,那么图中的菱形AEFG可以看成是把菱形ABCD以点A为旋转中心( )
A.顺时针旋转60°得到的
B.顺时针旋转120°得到的
C.逆时针旋转60°得到的
D.逆时针旋转120°得到的
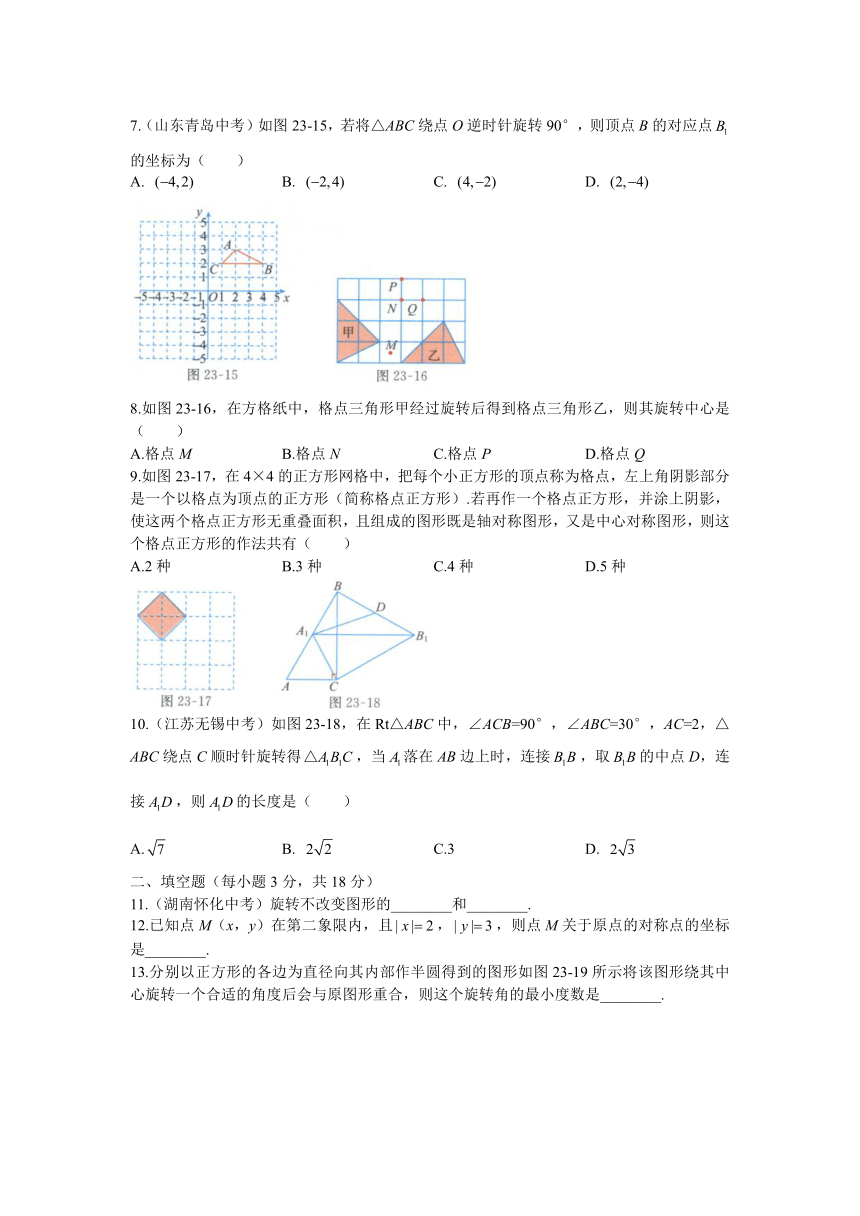
7.(山东青岛中考)如图23-15,若将△ABC绕点O逆时针旋转90°,则顶点B的对应点的坐标为( )
A. B. C. D.
8.如图23-16,在方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A.格点M B.格点N C.格点P D.格点Q
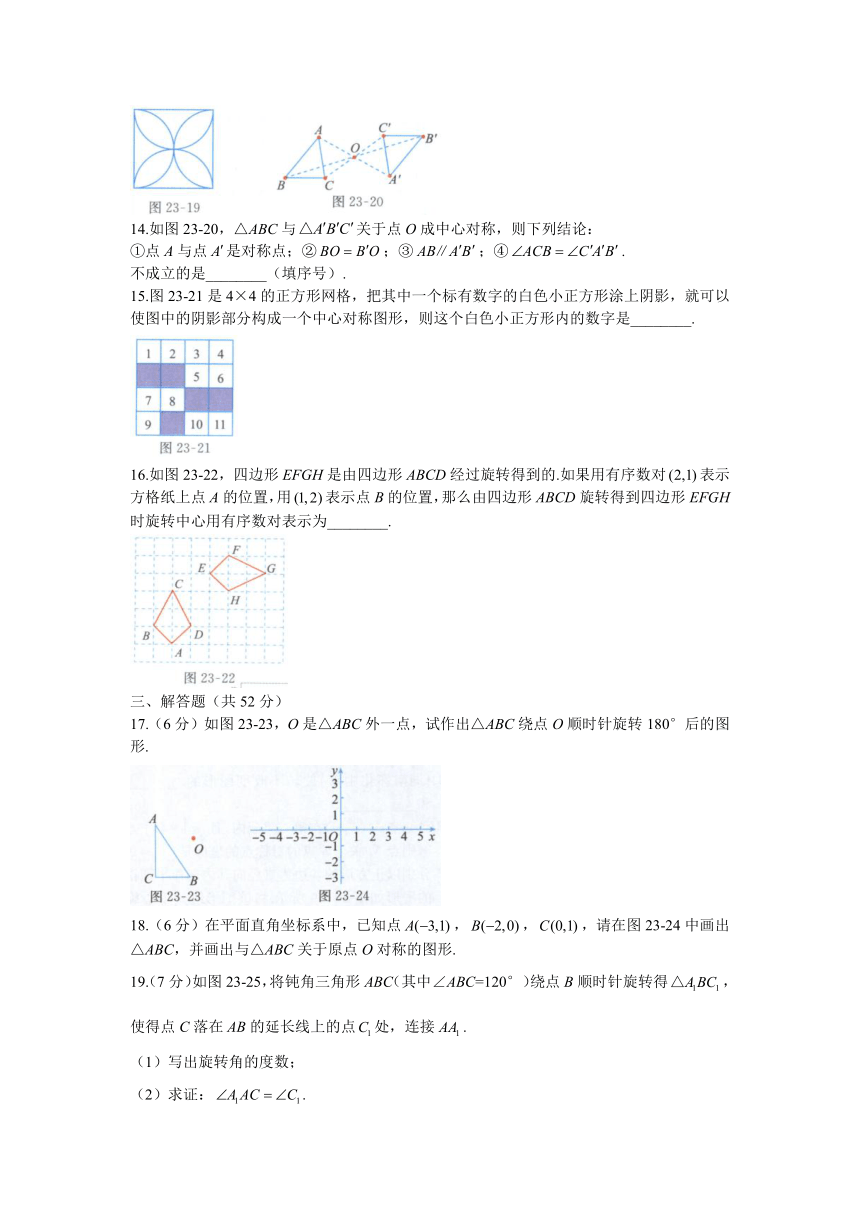
9.如图23-17,在4×4的正方形网格中,把每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种 B.3种 C.4种 D.5种
10.(江苏无锡中考)如图23-18,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得,当落在AB边上时,连接,取的中点D,连接,则的长度是( )
A. B. C.3 D.
二、填空题(每小题3分,共18分)
11.(湖南怀化中考)旋转不改变图形的________和________.
12.已知点M(x,y)在第二象限内,且,,则点M关于原点的对称点的坐标是________.
13.分别以正方形的各边为直径向其内部作半圆得到的图形如图23-19所示将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是________.
14.如图23-20,△ABC与关于点O成中心对称,则下列结论:
①点A与点是对称点;②;③;④.
不成立的是________(填序号).
15.图23-21是4×4的正方形网格,把其中一个标有数字的白色小正方形涂上阴影,就可以使图中的阴影部分构成一个中心对称图形,则这个白色小正方形内的数字是________.
16.如图23-22,四边形EFGH是由四边形ABCD经过旋转得到的.如果用有序数对表示方格纸上点A的位置,用表示点B的位置,那么由四边形ABCD旋转得到四边形EFGH时旋转中心用有序数对表示为________.
三、解答题(共52分)
17.(6分)如图23-23,O是△ABC外一点,试作出△ABC绕点O顺时针旋转180°后的图形.
18.(6分)在平面直角坐标系中,已知点,,,请在图23-24中画出△ABC,并画出与△ABC关于原点O对称的图形.
19.(7分)如图23-25,将钝角三角形ABC(其中∠ABC=120°)绕点B顺时针旋转得,使得点C落在AB的延长线上的点处,连接.
(1)写出旋转角的度数;
(2)求证:.
20.(7分)为了美化校园,学校准备在如图23-26所示的一块圆形空地上建花坛,现征集设计方案要求设计的图案由圆和等边三角形组成(圆和等边三角形的大小、个数不限),并且使整个圆形场地是一个中心对称图形.请画出你的设计方案.
21.(7分)(四川攀枝花中考)如图23-27,在平面直角坐标系中,直角三角形ABC的三个顶点分别是,,.
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△;
(2)分别连接,后,求四边形的面积.
22.(9分)如图23-28,P是矩形ABCD下方一点,将△PCD绕点P顺时针旋转60°后恰好点D与点A重合,得到△PEA,连接EB,△ABE是什么特殊三角形?请说明理由.
23.(10分)如图23-29所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转角,得到矩形FCDE,设FC与AB交于点H,且,.
(1)当时,△CBD的形状是什么?(直接写出答案)
(2)当AH=HC时,求直线HC对应的函数解析式.
参考答案
本章综合检测
1.B 解析:第1个图形和第3个图形既是轴对称图形,又是中心对称图形,共2个故选B.
2.C 解析:根据旋转的定义,可以得到旋转角为,因为是的外角,所以.
3.D 解析:因为是将绕原点顺时针旋转180°后得到的图形,所以点和点关于原点对称.又因为点的坐标为,所以点的坐标为.故选D.
4.B 解析:根据轴对称图形和中心对称图形的概念和性质逐一进行判断,选项A是中心对称图形,不是轴对称图形;选项B既是轴对称图形,又是中心对称图形;选项C是轴对称图形,不是中心对称图形选项D是轴对称图形,不是中心对称图形故选B
5.A 解析:正方形可由正方形绕点顺时针旋转180°得到;也可由正方形绕点顺时针旋转90°得到;也可由正方形绕点顺时针旋转270°得到故选A.
6.D 解析:旋转中心是点,点与点是一对对应点,旋转角是.因为和都是等边三角形,所以,所以,所以菱形可以看成是把菱形以点为旋转中心逆时针旋转120°得到的.
7.B 解析:如答图23-1,利用网格特征和旋转的性质,分别作出点的对应点,于是得到点的坐标为.故选B.
8.B 解析:如答图23-2,连接一组对应点,作对应点连线的垂直平分线,此垂直平分线过点.故点为旋转中心.
9.C 解析:如答图23-3,①②③④都分别和原来的格点正方形成的图形既是轴对称图形,又是中心对称图形,所以这个格点正方形的作法共有4种,故选C.
10.A 解析:如答图23-4,过点作,设与的交点为.
因为,,,所以,,所以.
因为,所以为等边三角形,所以,,所以,点为的中点,所以是的中位线,所以,.
由旋转的性质,知,,所以为等边三角形.
因为为中点,所以为等边三角形的高,且.
所以.
因为为的中点,且易证,所以为的中点,所以,.所以.
在中,,故选A.
11.形状 大小 解析:旋转不改变图形的形状和大小,只改变图形的位置.
12. 解析:因为点在第二象限内,所以,.又因为,,所以,.所以点关于原点的对称点的坐标是.
13.90°.
14.④ 解析:根据中心对称的性质可知,①②成立;根据,,,得,则,所以,故③成立;④中的两个角不是对应角,故④不成立.
15.3 解析:把标有数字3的白色小正方形涂上阴影,就可以使图中的阴影部分构成一个中心对称图形.
16. 解析:首先根据画出平面直角坐标系,然后用尺规作图作出线段,的垂直平分线(图略),垂直平分线的交点即为旋转中心.
17.解:①如答图23-5,连接并延长至,使,得的对应点;
②同样作法可得点,的对应点,;
③顺次连接,,,即为所求.
18.解:如答图23-6,就是所求作的三角形,,,三点关于原点的对称点分别为,,,是与关于原点对称的图形.
19.(1)解:旋转角的度数为60°.
(2)证明:因为点,,在同一条直线上,所以.
因为,所以,所以.
又因为,所以是等边三角形,所以,所以,所以.
由旋转的性质,得,所以.
20.解:设计的图形的特征为具有中心对称性,由于圆是中心对称图形,因此等边三角形的个数是偶数个时满足题意设计图形如答图23-7(答案不唯一)
21.解:(1)如答图23-8,为所求作的三角形.
(2)四边形的面积.
22.解:是等边三角形理由如下:
绕点顺时针旋转60°得到,的对应边是,的对应边是,旋转角为60°,即,所以是等边三角形,所以,所以,所以,所以,即.
又因为,所以是等边三角形.
23.解:(1)等边三角形.
(2)由题意,知,设点的坐标为,则,.
在中,,解得,所以点的坐标为.
设直线对应的函数解析式为,则有解得所以直线对应的函数解析式为.
(时间:60分钟 满分:100分)
、选择题(每小题3分,共30分)
1.(黑龙江鸡西中考)下列图形中,既是轴对称图形又是中心对称图形的个数为( )
A.1 B.2 C.3 D.4
2.如图23-12,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,在同一条直线上,那么旋转角等于( )
A.55° B.70° C.125° D.145°
3.在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到,若点B的坐标为,则点B的对应点的坐标为( )
A. B. C. D.
4.(江苏泰州中考)下列图案中,既是轴对称图形,又是中心对称图形的是( )
5.如图23-13,若正方形EFGH由正方形ABCD绕某点旋转得到,则可以作为旋转中心的是( )
A.点M或点O或点N B.点E或点O或点C
C.点E或点O或点N D.点M或点O或点C
6.图23-14是某个万花筒内部的图案,图中的小三角形均是全等的等边三角形,那么图中的菱形AEFG可以看成是把菱形ABCD以点A为旋转中心( )
A.顺时针旋转60°得到的
B.顺时针旋转120°得到的
C.逆时针旋转60°得到的
D.逆时针旋转120°得到的
7.(山东青岛中考)如图23-15,若将△ABC绕点O逆时针旋转90°,则顶点B的对应点的坐标为( )
A. B. C. D.
8.如图23-16,在方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A.格点M B.格点N C.格点P D.格点Q
9.如图23-17,在4×4的正方形网格中,把每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种 B.3种 C.4种 D.5种
10.(江苏无锡中考)如图23-18,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得,当落在AB边上时,连接,取的中点D,连接,则的长度是( )
A. B. C.3 D.
二、填空题(每小题3分,共18分)
11.(湖南怀化中考)旋转不改变图形的________和________.
12.已知点M(x,y)在第二象限内,且,,则点M关于原点的对称点的坐标是________.
13.分别以正方形的各边为直径向其内部作半圆得到的图形如图23-19所示将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是________.
14.如图23-20,△ABC与关于点O成中心对称,则下列结论:
①点A与点是对称点;②;③;④.
不成立的是________(填序号).
15.图23-21是4×4的正方形网格,把其中一个标有数字的白色小正方形涂上阴影,就可以使图中的阴影部分构成一个中心对称图形,则这个白色小正方形内的数字是________.
16.如图23-22,四边形EFGH是由四边形ABCD经过旋转得到的.如果用有序数对表示方格纸上点A的位置,用表示点B的位置,那么由四边形ABCD旋转得到四边形EFGH时旋转中心用有序数对表示为________.
三、解答题(共52分)
17.(6分)如图23-23,O是△ABC外一点,试作出△ABC绕点O顺时针旋转180°后的图形.
18.(6分)在平面直角坐标系中,已知点,,,请在图23-24中画出△ABC,并画出与△ABC关于原点O对称的图形.
19.(7分)如图23-25,将钝角三角形ABC(其中∠ABC=120°)绕点B顺时针旋转得,使得点C落在AB的延长线上的点处,连接.
(1)写出旋转角的度数;
(2)求证:.
20.(7分)为了美化校园,学校准备在如图23-26所示的一块圆形空地上建花坛,现征集设计方案要求设计的图案由圆和等边三角形组成(圆和等边三角形的大小、个数不限),并且使整个圆形场地是一个中心对称图形.请画出你的设计方案.
21.(7分)(四川攀枝花中考)如图23-27,在平面直角坐标系中,直角三角形ABC的三个顶点分别是,,.
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△;
(2)分别连接,后,求四边形的面积.
22.(9分)如图23-28,P是矩形ABCD下方一点,将△PCD绕点P顺时针旋转60°后恰好点D与点A重合,得到△PEA,连接EB,△ABE是什么特殊三角形?请说明理由.
23.(10分)如图23-29所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转角,得到矩形FCDE,设FC与AB交于点H,且,.
(1)当时,△CBD的形状是什么?(直接写出答案)
(2)当AH=HC时,求直线HC对应的函数解析式.
参考答案
本章综合检测
1.B 解析:第1个图形和第3个图形既是轴对称图形,又是中心对称图形,共2个故选B.
2.C 解析:根据旋转的定义,可以得到旋转角为,因为是的外角,所以.
3.D 解析:因为是将绕原点顺时针旋转180°后得到的图形,所以点和点关于原点对称.又因为点的坐标为,所以点的坐标为.故选D.
4.B 解析:根据轴对称图形和中心对称图形的概念和性质逐一进行判断,选项A是中心对称图形,不是轴对称图形;选项B既是轴对称图形,又是中心对称图形;选项C是轴对称图形,不是中心对称图形选项D是轴对称图形,不是中心对称图形故选B
5.A 解析:正方形可由正方形绕点顺时针旋转180°得到;也可由正方形绕点顺时针旋转90°得到;也可由正方形绕点顺时针旋转270°得到故选A.
6.D 解析:旋转中心是点,点与点是一对对应点,旋转角是.因为和都是等边三角形,所以,所以,所以菱形可以看成是把菱形以点为旋转中心逆时针旋转120°得到的.
7.B 解析:如答图23-1,利用网格特征和旋转的性质,分别作出点的对应点,于是得到点的坐标为.故选B.
8.B 解析:如答图23-2,连接一组对应点,作对应点连线的垂直平分线,此垂直平分线过点.故点为旋转中心.
9.C 解析:如答图23-3,①②③④都分别和原来的格点正方形成的图形既是轴对称图形,又是中心对称图形,所以这个格点正方形的作法共有4种,故选C.
10.A 解析:如答图23-4,过点作,设与的交点为.
因为,,,所以,,所以.
因为,所以为等边三角形,所以,,所以,点为的中点,所以是的中位线,所以,.
由旋转的性质,知,,所以为等边三角形.
因为为中点,所以为等边三角形的高,且.
所以.
因为为的中点,且易证,所以为的中点,所以,.所以.
在中,,故选A.
11.形状 大小 解析:旋转不改变图形的形状和大小,只改变图形的位置.
12. 解析:因为点在第二象限内,所以,.又因为,,所以,.所以点关于原点的对称点的坐标是.
13.90°.
14.④ 解析:根据中心对称的性质可知,①②成立;根据,,,得,则,所以,故③成立;④中的两个角不是对应角,故④不成立.
15.3 解析:把标有数字3的白色小正方形涂上阴影,就可以使图中的阴影部分构成一个中心对称图形.
16. 解析:首先根据画出平面直角坐标系,然后用尺规作图作出线段,的垂直平分线(图略),垂直平分线的交点即为旋转中心.
17.解:①如答图23-5,连接并延长至,使,得的对应点;
②同样作法可得点,的对应点,;
③顺次连接,,,即为所求.
18.解:如答图23-6,就是所求作的三角形,,,三点关于原点的对称点分别为,,,是与关于原点对称的图形.
19.(1)解:旋转角的度数为60°.
(2)证明:因为点,,在同一条直线上,所以.
因为,所以,所以.
又因为,所以是等边三角形,所以,所以,所以.
由旋转的性质,得,所以.
20.解:设计的图形的特征为具有中心对称性,由于圆是中心对称图形,因此等边三角形的个数是偶数个时满足题意设计图形如答图23-7(答案不唯一)
21.解:(1)如答图23-8,为所求作的三角形.
(2)四边形的面积.
22.解:是等边三角形理由如下:
绕点顺时针旋转60°得到,的对应边是,的对应边是,旋转角为60°,即,所以是等边三角形,所以,所以,所以,所以,即.
又因为,所以是等边三角形.
23.解:(1)等边三角形.
(2)由题意,知,设点的坐标为,则,.
在中,,解得,所以点的坐标为.
设直线对应的函数解析式为,则有解得所以直线对应的函数解析式为.
同课章节目录
