21.2 解一元二次方程 学案(含答案)
文档属性
| 名称 | 21.2 解一元二次方程 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 20:13:31 | ||
图片预览




文档简介
21.2 解一元二次方程
21.2.1 配方法
基础知识·细解读
知识点一 直接开平方法
1 直接开平方法的依据及实质
依据 实质
直接开平方法是解一元二次方程的最基本的方法,其依据是平方根的意义 解一元二次方程的基本思想是“降次”,通过“降次”把一元二次方程转化为一元一次方程.直接开平方法的实质就是把一个一元二次方程通过“降次”,转化为两个一元一次方程
2方程的根的情况
p的取值 方程的根的情况
有两个不相等的实数根,
有两个相等的实数根
没有实数根
【例1】用直接开平方法解下列方程:
(1); (2);
(3); (4).
解:(1)移项,得.
根据平方根的意义,得,即,.
(2)移项,得.二次项系数化为1,得.根据平方根的意义,得,即,.
(3)根据平方根的意义,得,即,.
(4)根据平方根的意义,得,即,.
知识点二 配方法
1 配方的目的和依据
目的 依据
降次,把一个一元二次方程转化成两个一元一次方程来解 完全平方公式:
2 用配方法解一元二次方程的一般步骤
示例 解题模板
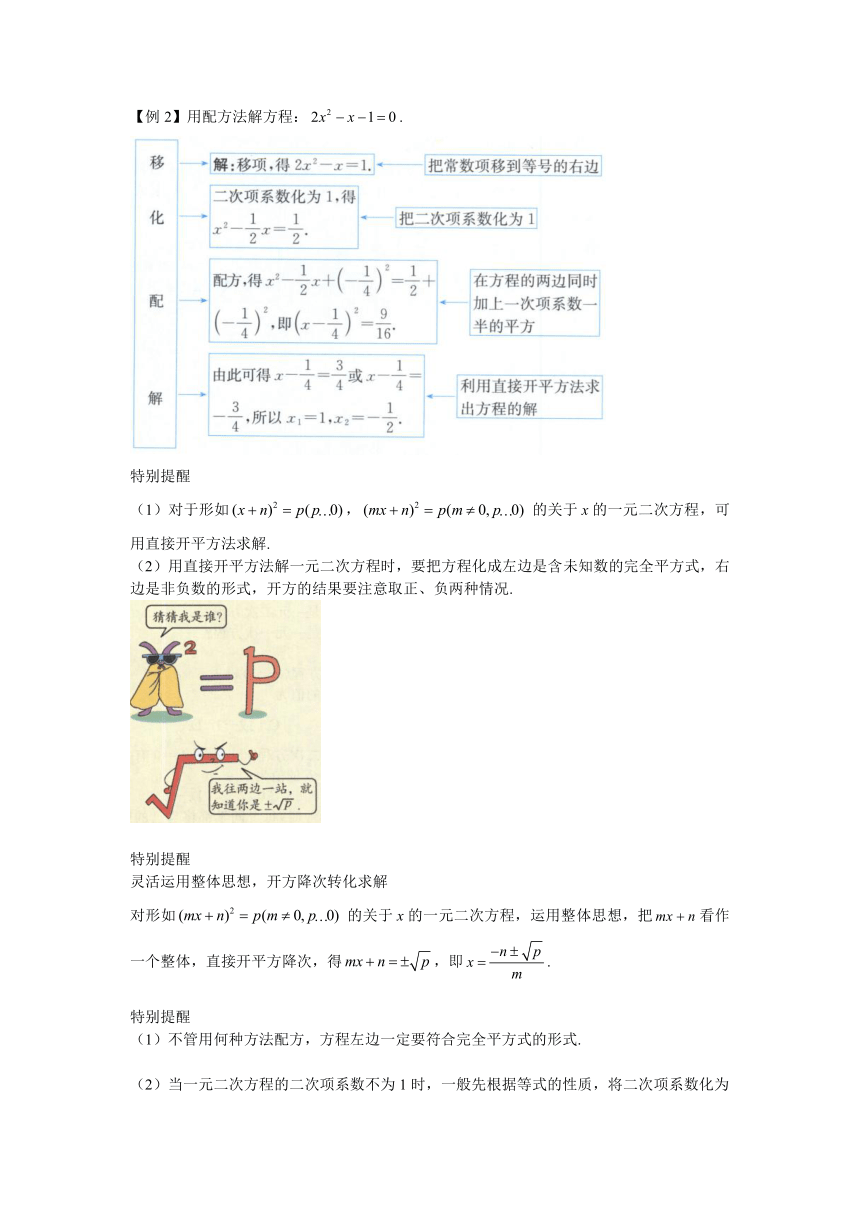
【例2】用配方法解方程:.
特别提醒
(1)对于形如,的关于x的一元二次方程,可用直接开平方法求解.
(2)用直接开平方法解一元二次方程时,要把方程化成左边是含未知数的完全平方式,右边是非负数的形式,开方的结果要注意取正、负两种情况.
特别提醒
灵活运用整体思想,开方降次转化求解
对形如的关于x的一元二次方程,运用整体思想,把看作一个整体,直接开平方降次,得,即.
特别提醒
(1)不管用何种方法配方,方程左边一定要符合完全平方式的形式.
(2)当一元二次方程的二次项系数不为1时,一般先根据等式的性质,将二次项系数化为1,再配方求解.
特别提醒
配方时易出现的错误
(1)移项忘记变号.
(2)系数化为1时漏项.
(3)方程两边没有同时加上一次项系数一半的平方.
应用能力·巧提升
题型一 用配方法解一元二次方程
【例1】用配方法解方程:.
审题关键:根据配方法的步骤解方程.
破题思路:移项→二次项系数化为1→配方→直接开平方解方程
解:移项,得.
二次项系数化为1,得.
配方,得,
即.
由此可得,
所以,.
新思路
亦可先把二次项系数化为1,再移项.
方法技巧
抓住关键点,配方变简单
用配方法解一元二次方程的关键步骤是方程两边同时加上一次项系数一半的平方.抓住此关键点,配方显得更简单.
题型二 配方法的应用
【例2】用配方法求的最小值.
审题关键:求一个代数式的最值,可用配方法,但要注意代数式中的配方与解方程中的配方的不同之处.
破题思路:先提出二次项系数,再加上一次项系数一半的平方,最后减去一个同样的数,配成完全平方形式,利用完全平方式的非负性,可求代数式的最值.
解:
.
因为,
所以的最小值为0,
所以的最小值是.
一题多变
当y取何实数时,式子有最大值?最大值是多少?
解后反思
配方法求代数式最值,“两点注意”别忘掉
(1)先把二次三项式配方成的形式.
①当时,该二次三项式有最大值k;
②当时,该二次三项式有最小值k.
(2)因为要求代数式中的配方是恒等变形,所以在加上一次项系数一半的平方后,应减去一个同样的数,使代数式的值保持不变.
变式训练
1.用配方法解方程:
(1);
(2).
变式训练
2.当x取何实数时,式子有最小值?最小值是多少?
3.试用配方法证明的值恒小于0.
易误易混·精辨析
易错点一 把握不好配方法的某些关键步骤而出错
【例1】用配方法解方程:.
解:移项,得.
配方,得,
即.
直接开平方,得,2
即.
所以,.
防错警示
在配方时,易因只在方程左边加上一次项系数一半的平方而方程右边不加,导致方程的两边不相等,出现错误.
由平方根的意义开平方时,应该是正、负两种情况,不要漏掉其中一种.
易错点二 用配方法时,二次项系数没有化为1而致错
【例2】用配方法解方程:.
解:移项,得.
二次项系数化为1,得.
配方,得,即.
直接开平方,得.
所以,.
防错警示
用配方法解一元二次方程时,为了便于配方,需将二次项系数化为1,如果未将二次项系数化为1就进行配方,方程的两边还是加上一次项系数一半的平方,那么方程的左边不能配成完全平方式.
真题解密·探源头
中考真题 教材原型
(安徽中考·8分)解方程:. 解:配方,得,………2分 即.……………………………4分 开平方,得,…………………6分 所以,.…………8分 教材第9页练习第2题(1) 解方程:. 解:移项,得. 配方,得, 即. 开平方,得. 所以,.
命题人解密:教材习题很典型地考查了用配方法解一元二次方程,中考题就是针对一元二次方程的解法这一考点进行设置的,不同的是中考题不用移项,可以直接配方求解. 阅卷人解密:解答此类题时的两处失分点:(1)配方时,易忽视在方程的两边同时加上一次项系数一半的平方,只把方程的一边变形;(2)开平方时漏掉负值,只取正值.
高效训练·速提能
【基础达标】
1.已知一元二次方程可转化为两个一元一次方程,其中一个一元一次方程是,则另一个一元一次方程是()
A. B. C. D.
2.一元二次方程的根是()
A. , B. ,
C. D.
3.一元二次方程配方后可变形为()
A. B.
C. D.
4.若是完全平方式,则m的值为________.
5.解下列方程:
(1);
(2);
(3).
【能力提升】
6.若关于x的方程的左边可以写成一个完全平方式,则k的值为()
A.10 B.10或14 C.-10或14 D.10或一14
7.将方程化为的形式,其中m,n是常数,则________.
8.当________时,式子有最大值,最大值是________.
9.用两种方法解方程:.
10.证明:关于x的方程,无论m取何值,该方程都是一元二次方程.
【拓展创新】
11.在实数范围内定义运算“”,其法则为,求方程的根.
12.选取二次三项式中的两项,配成完全平方式的过程叫做配方.例如:
①选取二次项和一次项配方:;
②选取二次项和常数项配方:或;
③选取一次项和常数项配方:.
根据上述材料,解决下面的问题:
(1)写出的两种不同形式的配方;
(2)已知,求x的值.
21.2.2 公式法
基础知识·细解读
知识点一 一元二次方程根的判别式
1 根的判别式及其表示
(1)根的判别式:一元二次方程根的判别式是.
(2)表示:通常用希腊字母“”表示,即.
2 一元二次方程实数根的情况
的符号 方程实数根的情况
有两个不相等的实数根
有两个相等的实数根
无实数根
注意:(1)一元二次方程有实数根包括一元二次方程有两个不相等的实数根和有两个相等的实数根.此时,切勿丢掉等号.
(2)当一元二次方程有两个相等的实数根时,一般不说方程只有一个实数根.
(3)当a,c异号时,一元二次方程一定有两个不相等的实数根.
【例1】下列一元二次方程没有实数根的是()
A. B. C. D.
解析:A选项,,方程有两个相等的实数根;B选项,方程可化为,,方程没有实数根;C选项,方程有两个不相等的实数根;D选项,方程可化为,,方程有两个不相等的实数根.故选B.
答案:B
总结
判别式的作用大,与0的大小关系的应用别弄错
根据一元二次方程根的判别式与0的大小关系可以判断根的情况,反之根的情况也可反映根的判别式与0的大小关系.解决问题时要注意区分与0的大小关系是条件还是结论.
知识点二 一元二次方程的求根公式及公式法
1 一元二次方程的求根公式
对一元二次方程进行配方,可得到一元二次方程的求根公式:.
2 一元二次方程的求根公式的推导过程(配方法)
↓移项
↓二次项系数化为1
↓配方
,
即
↓开平方
,
即
注意:(1)一元二次方程的求根公式的应用条件是,且.
(2)用求根公式可求出任何有解的一元二次方程的根.
3 用公式法解一元二次方程的一般步骤
示例 解题模板
【例2】用公式法解方程:.
特别提醒
区分“方程有实数根”与“一元二次方程有实数根”
(1)“方程有实数根”中的方程可以是一元一次方程,还可以是其他方程,只要有实数根即可.
(2)“一元二次方程有实数根”隐含两个条件:二次项系数不为0,且判别式为非负数.
特别提醒
一元二次方程求根公式的推导过程中,在最后开平方时,,式子前面有双重符号“±”,所以无论还是,等式右边最终结果仍为.
特别提醒
用公式法解一元二次方程的两点注意
(1)一定要先把方程化为一般形式,再确定a,b,c的值,注意不要出现符号错误.
(2)先计算的值,再确定是否代入求根公式求解.
巧记口诀
要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数a,b,c,计算根的判别式.判别式值与零比,有无实根便可知.若有实根套公式,若无实根要告之.
应用能力·巧提升
题型一 一元二次方程根的判别式的应用
角度1 不解方程,判断方程根的情况
【例1】已知一次函数,且当时,y随x的增大而增大,则关于x的方程的根的情况是()
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
审题关键:本题首先要由已知判断方程是否为关于x的一元二次方程,再计算一元二次方程根的判别式,最后根据与0的大小关系确定一元二次方程根的情况.
解析:因为对于一次函数,当时,y随x的增大而增大,所以,所以,所以是关于x的一元二次方程,所以,所以方程有两个不相等的实数根,故选A.
答案:A
解后反思
应用判别式的两点注意
(1)判别式只适合一元二次方程,不适合其他方程.
(2)注意隐含条件,即二次项系数.
角度2 根据一元二次方程根的情况,确定字母的取值范围
【例2】(山东聊城中考)如果关于x的一元二次方程有两个不相等的实数根,那么k的取值范围是________.
审题关键:根据关于x的一元二次方程有两个不相等的实数根,可知.由此可以构造出关于k的不等式,要注意二次项系数不等于0.
解析:由方程有两个不相等的实数根,得,则有,解得.由方程是一元二次方程,得.所以,且.
答案:,且.
方法技巧
应用“”,列出不等式(组)
在利用根的判别式求待定字母的取值范围时,首先要根据方程的根的情况判断与0的大小关系,然后利用题目中的条件列出关于所求字母的不等式(组),最后求解.
角度3 应用根的判别式证明方程一定有实数根
【例3】(甘肃白银中考)已知关于x的方程.
(1)若此方程的一个根为1,求m的值;
(2)求证:不论m取何实数,此方程都有两个不相等的实数根.
审题关键:本题考查的是方程的根的定义及一元二次方程根的判别式,解题的关键是配方法的熟练应用.
破题思路:(1)把x=1代入方程即可得到一个关于m的一元一次方程,解该方程即可.
(2)要证明一元二次方程有两个不相等的实数根,只要证明该一元二次方程根的判别式恒为正数即可.
(1)解:把x=1代入方程,得,解得.
(2)证明:.
因为(,所以,
即,
所以不论m取何实数,此方程都有两个不相等的实数根.
一题多变
若此方程的一个根为2,求m的值,并求此时方程的另一个根
方法技巧
利用根的判别式证明一元二次方程有实数根的技巧
在利用根的判别式证明一元二次方程有实数根时,首先找到判别式,并将判别式配方,然后利用配方的结果判定根的判别式恒大于等于0,即可得证.
题型二 用公式法解一元二次方程
【例4】用公式法解一元二次方程:
(1);
(2).
审题关键:按照用公式法解一元二次方程的方法与步骤解方程.
破题思路:
把方程化为一般形式→确定a,b,c的值→算出的值→代入公式求解
解:(1)因为,,,
所以,
所以,所以,.
(2)将方程去分母后整理成一般形式,
得,
这里,,.
因为,
所以.
所以原方程的根是.
过程释疑:
原方程移项,得.两边同乘8,得.
因为,所以原方程有两个相等的实数根.
一题多变
你能解方程吗?
解后反思
用公式法解一元二次方程的两点注意
(1)用公式法解一元二次方程的关键是对a,b,c的确定.
(2)判断与0的大小关系是求解中的重要一步,是用求根公式解一元二次方程的前提条件.
题型三 解含字母系数的一元二次方程
【例5】解关于x的方程.
审题关键:关于x的方程是指x是未知数,m,n是已知数,注意二次项的系数含字母时,要考虑其是否为0.
破题思路:分和两种情况讨论.当时,转化为一元一次方程求解;当时,按照一元二次方程的求解方
法求解.
解:当,且,时,,原方程可化为,即.
因为,所以.
当,且,时,因为,,,
所以,
所以,不论m是正数,还是负数,都有,.
方法技巧
类比数字系数方程,巧解字母系数方程
解含有字母系数的方程的方法就是把字母看作已知常数,解题方法与步骤和系数为数字时相同,不同的是有时要对系数进行讨论:先判断二次项的系数是否为0,若为0,则按一元一次方程来求解;若不为0,再确定a,b,c的值,求出的值,当时,套用求根公式进行求解.
变式训练
1.下列方程中,没有实数根的是()
A.
B.
C.
D.
2.(山东潍坊中考)关于x的一元二次方程根的情况,下列说法正确的是()
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.无法确定
3.(广西桂林中考)若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是()
A.
B. ,且
C. ,且
D.
4.若关于x的一元二次方程有实数根,则k的取值范围是()
A. B. C. D.
5.已知关于x的一元二次方程.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
变式训练
6.用公式法解方程:
(1);
(2);
(3);
(4).
变式训练
7.解关于x的方程:
.
8.解关于x的方程:
(其中,).
易误易混·精辨析
易错点一 因考虑不全而出错
【例1】已知关于x的一元二次方程有两个实数根,求k的取值范围.
解:
.
因为原方程有两个实数根,
所以,
即,解得.
防错警示
本题易因错把方程“有两个实数根”看作“有两个不相等的实数根”,导致列出错误的不等式.在解答问题时只有认真审题,考虑全面,才能避免出现错误.
易错点二 因未讨论方程中字母系数的取值而出错
【例2】(辽宁锦州中考)若关于x的方程有实数根,则k的取值范围是________.
解析:当时,原方程可化为,解得;当时,原方程为一元二次方程,.令,解得.所以当时,原方程有实数根.
答案:
防错警示
当二次项系数含有字母时,若方程未指明是一元二次方程,不能直接利用一元二次方程根的判别式解题,要认真审题,当已知条件不明确时,应分类讨论.
真题解密·探源头
中考真题 教材原型
(湖南怀化中考)一元二次方程的根的情况为() A.有两个不相等的实数根 B.有两个相等的实数根 C.只有一个实数根 D.没有实数根 解析:由题意,得,所以 方程有两个不相等的实数根.故选A. 答案:A 教材第17页习题21.2第4题(4) 利用判别式判断方程的根的情况: . 解:原方程可化为. 因为, 所以方程有两个不相等的实数根.
命题人解密:教材习题考查了直接利用一元二次方程根的判别式判断方程根的情况,中考题也是针对这一知识点进行命题的,只是题型有所改变. 阅卷人解密:解答此类题时的主要失分点:易因弄错a,b,c的符号,导致计算的值时出错.
中考真题 教材原型
(四川成都中考·6分)已知关于x的方程没有实数根,求实数m的取值范围. 解:因为关于x的方程没有实数根, 所以,…………………2分 所以,………………4分 即,解得. 所以实数m的取值范围是.……6分 教材第17页习题21.2第13题 无论p取何值,方程总有两个不等的实数根吗?给出答案并说明理由. 解:方程总有两个不等的实数根.理由如下: 原方程可化为,.因为不论p取何值,均成立,所以,所以方程总有两个不等的实数根.
命题人解密:教材习题和中考题均是利用判别式解决问题的题目,不同的是教材习题考查了利用判别式恒大于0证明一元二次方程总有两个不等的实数根,中考题是已知一元二次方程有无实数根的情况来确定判别式与0的大小关系,进而确定字母的取值范围. 阅卷人解密:在解答此类题时,要注意正确计算判别式,合理地将判别式合并变形,以达到解决问题的目的.
高效训练·速提能
【基础达标】
1.下列关于x的一元二次方程中,没有实数根的方程是()
A. B. C. D.
2.一元二次方程的解是()
A. , B. , C. , D. ,
3.若关于x的方程的一个根为1,则m的值为()
A.1 B. C.1或 D.1或
4.(湖南长沙中考)若关于x的一元二次方程有两个不相等的实数根,则实数m的取值范围是________.
5.(湖南张家界中考)若关于x的一元二次方程无实数根,则实数k的取值范围是________.
6.解下列方程:(1);
(2).
7.已知关于x的方程有两个相等的实数根,求m的值.
【能力提升】
8.(河北中考)已知a,b,c为常数,且,则关于x的方程的根的情况是()
A.有两个相等的实数根
B.有两个不相等的实数根
C.无实数根
D.有一个根为0
9.若关于x的方程有实数根,则a满足()
A. B.,且 C.,且 D.
10.(山东枣庄中考)若关于x的一元二次方程有两个不相等的实数根,则一次函数的图象可能是()
11.已知关于x的方程.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以这两根为边长的直角三角形的周长.
【拓展创新】
12.(四川巴中中考)定义新运算:对于任意实数m,n,都有.等式右边是常用的加法、减法、乘法及乘方运算.例如,.根据上述知识解决问题:若的值小于0,请判断方程2 的根的情况.
21.2.3 因式分解法
基础知识·细解读
知识点一 因式分解法
1 因式分解法
描述 利用因式分解来解一元二次方程的方法
理论依据 若两个因式的积为0,则这两个因式至少有一个为0,即若,则或
实质 将一个一元二次方程降次,转化为两个一元一次方程
2 适合用因式分解法求解的一元二次方程的特点
方程一边为0,另一边易于分解成两个一次因式乘积的形式.
3 利用因式分解解一元二次方程的常用方法
(1)提公因式法:把多项式各项的公因式提到括号外面,将多项式写成因式乘积的形式.
(2)逆用平方差公式和完全平方公式来分解因式.
4 利用因式分解法解一元二次方程的一般步骤
示例 解题模板
【例】用因式分解法解方程:.
总结
两种常见的用因式分解法求解的方程
(1)解形如的一元二次方程时,将方程的左边运用提公因式法因式分解为,则或,即,.
(2)解形如的一元二次方程时,将方程的左边运用平方差公式因式分解为,则或,即,.
知识点二 灵活选用合适的方法解一元二次方程
求解一元二次方程的各种方法的特点及举例
方法 特点 举例
直接开平方法 解一元二次方程最简单的方法.若方程可化为 的形式,则宜选用直接开平方法求解 . 解:直接开平方,得 或, 所以,
配方法 解一元二次方程最基本的方法,它适用于解所有的一元二次方程.配方法要先配方,再降次.通过配方法可以推出求根公式 . 解:移项、配方,得. 开平方,得或, 所以,
公式法 解一元二次方程最通用的方法,它适用于解所有的一元二次方程.公式法是直接利用求根公式解方程 . 解:移项,得, 所以,,. 因为 ,所以, 所以,
因式分 解法 解一元二次方程较简单的方法.当方程的一边为0,另一边易化为两个一次因式的积时,就可优先选用因式分解法求解 . 解:移项,得. 因式分解,得. 于是得或, 所以,
特别提醒
(1)因式分解法只能解某些特殊的一元二次方程,不是所有的一元二次方程都能用因式分解法求解.
(2)用因式分解法解一元二次方程时,一定要把方程的右边化为0,否则会出现错误.
(3)用因式分解法解方程时,不要将方程两边同时除以含有未知数的式子,这样容易丢根.
巧记口诀
利用因式分解法解一元二次方程的12字口诀
右化零,左分解,
两因式,各求解.
拓展
解形如的一元二次方程时,将其左边因式分解,则方程化为,所以或,即,.
特别提醒
求解一元二次方程的方法的灵活选择
(1)直接开平方法只适用于一些特殊结构的一元二次方程.如,,等形式的方程.
(2)当一元二次方程的二次项系数为1,一次项系数为偶数时,用配方法比较简单.
(3)公式法是由配方法推导出来的,故能用公式法求解的一元二次方程一定可以用配方法来求解.
当解一个一元二次方程用其他方法都不简单时,可选用公式法.
(4)因式分解法只适用于方程一边等于0,另一边易于分解因式的一些特殊方程.
应用能力·巧提升
题型一 用因式分解法解一元二次方程
角度1 运用提公因式法分解因式解一元二次方程
【例1】用因式分解法解下列方程:
(1); (2)(甘肃兰州中考);
(3).
审题关键:用因式分解法解一元二次方程,一般先把方程移项整理化成右边为0的形式,观察方程的特点,通过变形,能提公因式的要提公因式.
破题思路:(1)移项变形,可提公因式x进行分解因式求解.(2)把原方程变形,可把y+2看作一个整体,提公因式进行因式分解求解.(3)把原方程变形,可把x-2看作一个整体,提公因式进行因式分解求解,注意符号变化.
解:(1)移项,得.因式分解,得.于是得或,解得,.
(2)将原方程变形为.移项,得.因式分解,得.于是得或,解得,.
(3)将原方程移项变形为.因式分解,得.
于是得或,
解得,.
新思路
此处也可把看作一个整体,把方程变形,提公因式进行因式分解来求解.
解后反思
在用因式分解法解一元二次方程时,千万不要急于把方程化成一般形式,要先观察方程的特点,能提公因式进行因式分解的就提公因式进行因式分解.如本例(3),把看作一个整体提公因式进行因式分解的方法比较简单.
角度2 运用平方差公式(或完全平方公式)分解因式解一元二次方程
【例2】用因式分解法解下列方程:
(1);
(2).
审题关键:观察方程特点,可用公式法分解因式的应先用公式法分解因式,再解方程.
破题思路:(1)可把写成,利用平方差公式分解因式求解.(2)先将移项、变号,再用平方差公式对因式分解,最后提公因式分解因式求解.
解:(1)原方程可化为.
因式分解,得.
整理,得,
于是得或,解得,.
(2)整理,得,
即.
因式分解,得,
即.
整理,得,
于是得或,所以,.
解后反思
分解因式时可以利用如,等式子,把互为相反数的两个代数式进行转换,进而可以运用公式较容易地找到公因式,使问题得解.
角度3 利用因式分解法解型的一元二次方程
【例3】用因式分解法解方程:.
审题关键:可利用进行因式分解.
破题思路:要设法找到两个数p,q,使,.
解:原方程可化为,
于是得或,
所以,.
方法技巧
利用因式分解法解型一元二次方程的技巧
形如的一元二次方程可尝试利用因式分解法求解,进行因式分解时,必须保证常数项拆成的两个因数的和为一次项系数,两个因数的积为常数项,另外两根的符号与拆成的两因数的符号正好分别相反.
题型二 用适当的方法解一元二次方程
【例4】选择适当的方法解下列方程:
(1);
(2);
(3);
(4).
审题关键:已知解一元二次方程的四种方法:直接开平方法、因式分解法、配方法和公式法.应根据方程特点,选择适当的方法求得方程的解.
破题思路:(1)先化为一般形式,根据方程的特点,可用公式法求解.(2)根据方程的特点,可先移项,用因式分解法求解,也可用直接开平方法求解.(3)先化为一般形式,根据方程的特点,可用因式分解法求解.(4)先化为一般形式,根据方程的特点,可用配方法求解.
解:(1)移项,得.
故,,,.
所以.
所以,.
(2)方法1:移项,得.
因式分解,得.
所以或.
所以,.
方法2:直接开平方,得,
所以,.
(3)原方程可化为,
即,所以.
(4)原方程可化为,
即.所以.所以,.
方法技巧
选择合适方法,轻巧求解一元二次方程
解一元二次方程要根据方程特点,合理变形,采用合适的方法.方法选择的一般顺序:直接开平方法→因式分解法→公式法→配方法.
变式训练
1.方程的解是()
A.
B.
C.,
D.,
2.解方程:
(1);
(2).
3.用因式分解法解方程:
.
4.(山西中考)解方程:
.
5.(辽宁沈阳中考)一元二次方程的根是()
A.,
B.,
C.,
D.,
6.解方程:
.
变式训练
7.选择适当的方法解下列方程:
(1);
(2);
(3);
(4).
易误易混·精辨析
易错点一 错用等式的性质
【例1】解方程:.
解:移项,得.所以.所以或.
所以,.
防错警示
本题易出现方程的两边同除以得的错误.这是因为当时,不符合等式的性质,因此,方程的两边不能同除以含未知数的式子.
易错点二 用因式分解法求解方程时,方程右边未化为0而出错
【例2】解方程:.
解:将方程整理,得.
因式分解,得.
所以或.
所以,.
防错警示
①用因式分解法解一元二次方程时,必须先使方程的右边为0才可将另一边的多项式分解因式求解.
真题解密·探源头
中考真题 教材原型
(四川巴中中考)解方程:. 解:移项,得. 整理,得. 所以或. 解得,. 教材第17页习题21.2第6题(3) 用因式分解法解方程: . 解:原方程可化为, 所以或, 所以,.
命题人解密:教材习题很典型地考查了用因式分解法解一元二次方程,中考题就是针对因式分解法解一元二次方程这一考点进行设置的,方程形式非常相近,解题方法也相同. 阅卷人解密:解答此类题时的两处失分点:(1)移项时忘记变号;(2)转化为两个一元一次方程时漏掉一个.
高效训练·速提能
【基础达标】
1.一元二次方程的解是()
A. B. C., D.,
2.方程的根为()
A. B. C., D.
3.解方程①;②;③时,解法选择较为恰当的是()
A.全部用公式法
B.①用直接开平方法,其余都用公式法
C.全部用配方法
D.分别用直接开平方法、公式法、因式分解法
4.(1)方程的解是________;
(2)方程的解是________.
5.用因式分解法解下列方程:
(1);
(2);
(3).
6.先阅读材料,再解答问题.
小聪和小明在解一元二次方程时,采用了不同的方法.
小聪:移项,得.
直接开平方,得.
解得,.
小明:将原方程变形,得.
整理,得________________.
所以或.
所以,.
小聪和小明解方程分别运用的什么方法?横线上应填什么?
【能力提升】
7.(青海中考)已知等腰三角形的腰和底的长分别是一元二次方程的根,则该三角形的周长为()
A.8 B.10 C.8或10 D.12
8.已知关于x的一元二次方程的一个实数根为1,那么它的另一个实数根是()
A.-2 B.0 C.1 D.2
9.设a,b为方程的两根,,则的值为________.
10.用适当的方法解下列方程:
(1);(2);
(3);(4).
11.(一题多解)至少用两种方法解方程:.
【拓展创新】
12.定义新运算“”如下:当时,;当时,.若,则x的值是________.
13.探究下表中的奥秘,并完成填空:
一元二次方程 两个根 二次三项式因式分解
,
,
,
,
______, ______
将你发现的结论一般化,并写出来.
*21.2.4一元二次方程的根与系数的关系
基础知识·细解读
知识点一 元二次方程的根与系数的关系
方程的根与系数的关系
数学语言 设的两个根为,,则,
文字语言 一元二次方程的两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比
使用条件 (1)方程是一元二次方程,即二次项系数; (2)方程有实数根,即
重要推论 设一元二次方程的两根为,, 则,
常见变形 (1); (2); (3); (4); (5); (6)
【例】根据一元二次方程的根与系数的关系,求下列方程的两根,的和与积.
(1);(2);(3).
解:(1),.
(2)整理,得,
所以,.
(3),.
总结
利用一元二次方程的根与系数的关系求两根的和与积的两点注意
(1)一元二次方程必须有两个实数根().
(2)中的负号与方程中a,b的符号不要混淆.
拓展
利用一元二次方程的根与系数的关系进一步讨论根的符号
设一元二次方程的两根为,,则
,且 两根同为正数
两根同为负数
,且 两根异号且正根的绝对值较大
两根异号且负根的绝对值较大
应用能力·巧提升
题型一 一元二次方程根与系数关系的应用
角度1 已知一个根,利用根与系数的关系求另一个根
【例1】(山东潍坊中考改编)已知关于x的方程有一个根是,求另一个根.
审题关键:本题考查了一元二次方程的根与系数的关系及根的定义,解题的关键是记住一元二次方程的根与系数的关系及熟练掌握一元二次方程的解法,并能灵活运用.
破题思路:思路1:利用根与系数的关系直接列出关于另一个根的方程号求解即可;思路2:先把代入原方程,求得m的值,再解方程求出另一个根.
解:方法1:设方程的另一个根是,由一元二次方程的根与系数的关系,得,解得.
所以方程的另一个根是-4.
方法2:把代入原方程,得,解得.
所以原方程为,解得,.
所以方程的另一个根是-4.
方法技巧
已知一元二次方程的一个根,求另一个根的方法
(1)方法1(利用根与系数的关系):当方程的二次项系数、一次项系数已知,常数项未知时,利用两根的和求另一个根;当方程的二次项系数、常数项已知,一次项系数未知时,利用两根的积求另一个根
(2)方法2(利用根的定义):先把方程的已知根代入方程求出未知系数或常数项,再解方程求另一个根.
角度2 利用根与系数的关系求某些代数式的值
【例2】(山东德州中考)若方程的两根为,,则________.
审题关键:本题求解的关键是利用根与系数的关系,,将所求的代数式变形为含和的式子.
解析:因为方程的两根为,,所以,,所以.
答案:
方法技巧
巧用根与系数的关系,求特殊代数式的值
算→计算出,的值
↓
变→将所求的代数式变形为用和表示的式子
↓
代→代入所求的代数式计算
角度3 利用根与系数的关系确定待定字母的值
【例3】(湖北鄂州中考)已知关于x的一元二次方程有两个不等实根,.
(1)求实数k的取值范围;
(2)若方程两实根,满足,求k的值.
审题关键:根据判别式的符号可求得k的取值范围;由,可考虑利用一元二次方程的根与系数的关系求解.
破题思路:(1)由于方程有两个不等实根,故其根的判别式,列不等式可确定实数k的取值范围.(2)先讨论两根的符号,再去掉中的绝对值符号,最后根据根与系数的关系,可得关于k的一元二次方程,求得k的值.
解:(1)因为原方程有两个不相等的实数根,所以
,解得
(2)因为,所以.
因为,所以,.
所以.
因为,所以.
所以或.因为,所以.
解后反思
使用根与系数的关系的前提——
利用一元二次方程根与系数的关系求方程的系数时,千万不要忘记将系数代回验证是否成立,因为根与系数的关系是在一元二次方程中的前提下使用的.
题型二 已知两数的和与积,构造一元二次方程解决问题
【例4】已知两个数的和是8,积为15,求这两个数.
审题关键:可利用一元二次方程的根与系数的关系,根据两个数的和与积构造一元二次方程求这两个数.
破题思路:根据一元二次方程的根与系数的关系,可用一8作为一次项系数,15作为常数项,构造一个二次项系数是1的一元二次方程,则这个一元二次方程的根就是所要求的两个数.
解:根据一元二次方程的根与系数的关系,知要求的两个数是方程的两个根,解这个方程得,.所以这两个数是3,5.
方法技巧
已知两数和与积,巧构一元二次方程求两数
把已知两个数的和与积分别看成一元二次方程两个根的和与积,则可根据“方程能化为”构造一个符合要求的一元二次方程来求这两个数.
变式训练
1.(山东枣庄中考)已知关于x的方程有一个根为-2,则另一个根为()
A.5 B.-1 C.2 D.-5
2.若是关于x的方程的一个根,试求方程的另一个根.
3.已知m,n是方程的两个实数根,则的值为()
A.-1 B. C. D.1
4.(广西玉林中考)若关于x的一元二次方程有两个实数根,,则()
A. B. C.4 D.-4
5.已知关于x的一元二次方程.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根为,,且满足,求实数m的值.
变式训练
6.已知实数,满足,,则以,为根的一元二次方程是()
A.
B.
C.
D.
易误易混·精辨析
易错点一 用根与系数的关系解题时,忽视对判别式的检验而致错
【例1】已知关于x的方程,下列说法正确的是()
A.若两根是,,则
B.若两根是,,则
C.若两根是,,则
D.以上说法都不对
解析:因为,
所以方程没有实数根.
故选D.
答案:D
防错警示
本题易因忽视一元二次方程的根与系数的关系使用的前提条件,而错选A或C.使用一元二次方程的根与系数的关系解题时,要注意检验是否成立.
易错点二 忽视题干中的隐含条件而致错
【例2】已知关于x的方程的两个根互为相反数,求k的值.
解:由题意可知,,即,
解得.
由于,
当时,,不合题意,舍去;
当时,,
又因为,符合题意.
所以.
防错警示
应用一元二次方程的根与系数的关系解题时,要关注已知中的隐含条件.本题易因未检验方程的判别式及忽视与互为相反数,未舍去不合题意的而出错.
真题解密·探源头
中考真题 教材原型
(四川凉山州中考)已知,是一元二次方程的两根,则的值是 A. B. C. D. 解析:把一元二次方程化为一般形式为,于是,,因此 .故选D. 答案:D 教材第16页练习(1) 不解方程,求方程两个根的和与积: . 解:设方程的两个根为和. 移项,得. 根据根与系数的关系,得, .
命题人解密:教材习题考查了直接利用一元二次方程的根与系数的关系求两根的和与积.中考题是针对一元二次方程的根与系数的关系,求与两根的和与积有关的简单代数式的值,难度稍高于教材习题. 阅卷人解密:在解答此类题时的两处失分点:(1)易弄错两根的和或积的符号;(2)易把代数式变形错误
高效训练·速提能
【基础达标】
1.(湖北黄冈中考)若方程的两个实数根分别为,,则()
A.-4 B.3 C. D.
2.(江西中考)设,是一元二次方程的两个根,则的值是()
A.2 B.1 C.-2 D.-1
3.(浙江金华中考)一元二次方程的两根为,,则下列结论正确的是()
A. , B. , C. D.
4.(山东威海中考)已知,是关于x的方程的两实数根,且,则的值是()
A. B. C.4 D.-1
5.(湖北黄石中考)若关于x的一元二次方程的两实数根之积为负数,则实数m的取值范围是________.
6.(湖北恩施州中考)已知一元二次方程的两根为m,n,则________.
7.已知两个数的和是10,积为21,求这两个数.
【能力提升】
8.(山东烟台中考)若,是一元二次方程的两个根,则的值为()
A.-1 B.0 C.2 D.3
9.已知关于x的一元二次方程的两个实数根为,,若,则m的值为________.
10.如果m,n是两个不相等的实数,且满足,,那么代数式________.
11.已知关于x的方程.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)当该方程的一个根为1时,求a的值及方程的另一根.
【拓展创新】
12.关于x的方程有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使方程的两个实数根的倒数
和等于0?若存在,求出k的值;若不存在,说明理由.
本书参考答案
21.2 解一元二次方程
21.2.1 配方法
应用能力·巧提升
1.解:(1)移项,得.配方,得,即.由此可得,所以,.
(2)二次项系数化为1,得.移项、配方,得,即,所以.
所以,.
【例2】一题多变
解:
.
因为,所以的最大值为0,所以当时,原代数式有最大值,最大值是.
2.解:因为可配方为,无论x取何实数,,所以当时,有最小值1.
3.证明:
.
因为
所以,
所以.
因此,的值恒小于0.
高效训练·速提能
1.D 解析:,直接开平方,得,则或.故选D.
2.D 解析:原方程可变形为.根据平
方根的意义,得.故选D.
3.A 解析:移项,得.配方,得,即.故选A.
4. 解析:根据完全平方式的结构特征,知,所以.
5.解:(1)原方程可化为.开平方,得,所以,.
(2)二次项系数化为1,得,即.开平方,得.所以,.
(3)移项,得.
配方,得,即.
开平方,得或,所以,.
6.D 解析:方程的左边变形为,所以,即或,解得或.故选D.
7.55 解析:将移项,得.配方,得,即,所以,,所以.
8.4 21 解析:.
当时,有最大值21.
9.解:方法1(配方法):展开,得.
移项、合并同类项,得.
二次项系数化为1,得.
配方,得.
直接开平方,得,
所以,.
方法2(直接开平方法):原方程可化为.
直接开平方,得或,解得,.
10.证明:二次项系数.
因为,所以,
即.
所以无论m取何值,该方程都是一元二次方程
11.解:因为,
所以.
所以.所以.
所以,即,.
12.解:(1)
.
(2)因为,
所以,
所以,,
所以,,所以.
21.2.2 公式法
应用能力·巧提升
1.B 解析:方程的根的判别式等于,所以方程没有实数根.
2.A 解析:
,
因为,即,
所以方程有两个不相等的实数根,故选A.
3.B 解析:因为关于x的一元二次方程(有两个不相等的实数根,所以
即所以,且.
故选B
4.D 解析:因为一元二次方程有实数根,所以,解得.故选D.
【例3】一题多变
解:把代入方程,得,解得.
所以原方程为,
即.
解得,.
所以此时方程的另一个根是.
5.(1)证明:原方程可化为,
所以.
因为,所以,即.
所以对于任意实数m,方程总有两个不相等的实数根.
(2)解:把代入原方程得.解得
.所以原方程可化为.解得
,.所以方程的另一个根是4.
【例4】一题多变
解:因为,,,所以,所以方程没有实数根.
6.解:(1)因为,,,
所以.
所以,
所以,.
(2)方程化为.
因为,,,
所以,
所以,
所以.
(3)方程化为.
因为,,,
所以,
所以原方程无实数根,
(4)方程化为3.
因为,,,
所以,
所以,
所以,.
7.解:①当,即时,原方程化为,所以.
②当,即时,.
当,即,且时,方程有两个不相等的实数根,
,;
当时,方程有两个相等的实数根,
;
当时,方程没有实数根.
8.解:将原方程化为一般形式为.
因为,,,
所以
,
所以,
所以,.
高效训练·速提能
1.C 2.A
3.D 解析:把代入方程可得,所以,
,所以,
即,故选D.
4. 解析:由题意,得,解得.
5. 解析:因为关于x的一元二次方程无实数根,所以.因为,,,
所以,即.所以.
6.解:(1)方法1:移项,得.
配方,得,即,
由此可得,
即,.
方法2:因为,,,
所以.
所以,
所以,.
(2)原方程可化为,
所以,,,
所以,
所以,
所以,.
7.解:因为关于x的方程有两个相等的实数根,
所以.
所以.
所以,.
8.B 解析:因为,即,
所以,,.所以关于x的方程是一元二次方程,且,
故该方程有两个不相等的实数根.当方程有一个根为0时,将代入方程,得,这与矛盾,D项错误.故选B.
9.A 解析:当时,有实数解,此时;当时,应满足,解得.综上所述,
.故选A
10.B 解析:因为关于x的一元二次方程有两个不相等的实数根,所以,即,所以.所以k,b异号,选项A中,,,所以选项A错误;选项B中,,.所以选项B正确:选项C中...所以选项C错误;选项D中,,所以选项D错误,故选B
11.(1)证明:
.
因为,所以,所以方程恒有两个不相等的实数根.
(2)解:把代入方程,得,所以方程为,解得,.
所以方程的另一个根是3.
①当1和3都是直角三角形的直角边长时,由勾股定理,知斜边长为,所以直角三角形的周长为;
②当3为直角三角形的斜边长时,由勾股定理,知另一条直角边长为,所以直角三角形的周长为.
综合①②,知以这两根为边长的直角三角形的周长为或.
12.解:由定义新运算的法则,知.
2☆a的值小于0,即,解得.
方程的根的判别式.
因为,,所以,所以,故方程有两个不相等的实数根.
21.2.3 因式分解法
应用能力·巧提升
1.D 解析:因为,
所以,
所以,
所以,.
2.解:(1)移项,得.
因式分解,得.
于是得或,
解得,.
(2)移项,得.
因式分解,得.
于是得或,
解得,.
3.解:移项,得,
即.
因式分解,得.
整理,得,于是得或,解得,.
4.解:原方程可化为.
移项,得.
提公因式,得.
整理,得.
所以或.
所以,.
5.B 解析:方程整理,得.因式分解,得.解得,.故选B
6.解:原方程可化为,
因式分解,得.
解得,.
7.解:(1),由求根公式,
得.
所以,.
(2)直接开平方,得.
所以,.
(3)移项,得.
因式分解,得.
于是得或.
所以,.
(4)配方,得.所以.
所以,.
高效训练·速提能
1.C 解析:原方程为,所以或,所以,.故选C.
2.C 解析:方程整理,得.所以.解得,.
3.D 解析:根据方程的特征可知选D.
4.(1), 解析:由因式分解法可将原方程化为.所以或.所以,.
(2), 解析:原方程可化为.所以或.
解得,.
5.解:(1)因式分解,得.
整理,得.所以或.所以,.
(2)因式分解,得.于是有或.所以,.
(3)因式分解,得.
整理,得.所以或.
所以,.
6.解:由小聪将方程先移项再开平方,知他用的是直接开平方法;
小明将方程分解为两个因式的乘积,他用的是因式
分解法.故应填.
7.B 解析:因为,所以,,故三角形三边长可能为2,2,4或2,4,4,但由于,所以2,2,4不能构成三角形,所以该三角形的周长为.
8.A 解析:因为关于x的一元二次方程的一个实数根为1,所以把代入一元二次方程,得,解得.所以原方程为,所以,所以,.故选A.
9.-6 解析:原方程变形,得.因式分解,得.所以,.因为,所以,,故.
10.解:(1)方程整理,得.
所以,所以,.
(2)因为,,,
所以,
所以,
所以,.
(3)方程整理,得,
即.
所以或,
所以,.
(4)移项,得.
配方,得,
即.
所以,所以,.
11.解:方法1(配方法):配方,得
,
即,所以,
所以,.
方法2(公式法):整理,得,
因为,,,
所以,
所以,
所以,.
方法3(因式分解法):整理,得.
分解因式,得,
所以或,
所以,.
12.-1或 解析:若,即,根据定义,得
,解得,,这两个解均符合题意;若,即,根据定义,得,解得,,这两个解均不符合题意.综上所述,,.
13.解:依次填:,-3,,3.
发现的结论:若一元二次方程的
两个根为,,则.
21.2.4 一元二次方程的根与系数的关系
应用能力·巧提升
1.B 解析:方法1:设另一个根为x1.因为关于x的方程有一个根为-2,所以,解得,所以另一个根为-1.故选B.
方法2:把代入方程,得,解得,所以原方程为,解得,.故选B.
2.解:方法1:因为关于x的方程有一个根,所以,所以.
方法2:把代入方程,得,解得,所以原方程为,解得,.
3.A 解析:因为m,n是方程的两个实数根,所以,,所以.故选A.
4.D 解析:因为,,
所以.故选D.
5.解:(1)因为方程有实数根,所以,所以.
(2)因为方程的两实数根为,,所以.①
又因为,②
联立①②并解方程组,得
所以.
6.A 解析:以,为根的一元二次方程是,所以满足条件的是.
高效训练·速提能
1.D 解析:因为方程的两个实数根分别为,,,,所以.故选D.
2.D 解析:.故选D.
3.C 解析:将代入,得,所以不是方程的根,故A选项错误;将代入,得,所以不是方程的根,故B选项错误;由一元二次方程的根与系数的关系,得,,故C选项正确,D选项错误.故选C.
4.A 解析:由根与系数的关系,得,,所以,,所以,,所以的值是.故选A.
5. 解析;设,为方程的两个实数根,由已知,得,即,解得.
6. 解析:由题意,得,由一元二次方程根与系数的关系,得,,所以.
7.解:根据根与系数的关系,知两个数是方程的两个根,解这个方程,得,
.所以这两个数是3,7.
8.D 解析:因为,是一元二次方程的两个根,所以,,所以.故选D.
9.2或-6 解析:根据题意,得,.又因为,
所以,解得,,并且当或-6时方程都有解,所以m的值为2或-6.
10.2032 解析:由题意可知,m,n是的两个不相等的实数根.根据根与系数的关系,知..又因为,
所以
.
11.解:(1)根据题意,得0,解得.
(2)方法1:设原方程的另一根为,由根与系数的关系,得
解得
所以a的值是-1,原方程的另一根为-3.
方法2:把代入原方程,得,解得,所以原方程为,解得,.
所以,原方程的另一根为-3.
12.解:(1)根据题意,得,所以.又因为,所以k的取值范围是,且.
(2)不存在符合条件的实数k,理由如下:
假设存在符合条件的实数k,设方程的两根分别为,,由根与系数的关系,得,.因为,所以,所以.
由(1),知当时,,原方程无实数根.
所以不存在符合条件的实数k.
教材参考答案
21.2 解一元二次方程
练习(第6页)
解:(1),所以,所以,.
(2),移项,得,,所以,.
(3),移项,得
所以,所以,.
(4),移项,整理,得,
所以,所以,.
(5)可化为,
所以,所以,.
(6),移项,得,所以,所以.
因为,所以原方程无实数根.
问题(第7页)
两边加9,可以将方程左边配成完全平方形式,若加其他数则不行
练习(第9页)
1.(1)25 5(2)36 6(3) (4)
2解:(1),,,,
故,.
(2),,,,
故,.
(3),,,,,,故,.
(4),,,,
所以,.
(5),,,故原方程无实数根.
(6),,,,故,.
练习(第12页)
1.解:(1),因为,,,
所以,
所以,所以,.
(2),因为,,,
所以,所以.
所以,.
(3),因为,,,
所以,所以,
所以,.
(4),因为,,,所以,所以,所以,.
(5),整理,得,
因为,,,
所以,所以,
所以,.(当得出时,也可移项后,直接开平方得结果)
(6),整理,得,因为,,,
所以,
所以,所以,.
2.解:,因为,,,
所以,所以,所以,(不符合题意,舍去).
答:铁皮各角应切去边长为5cm的正方形.
练习(第14页)
1.解:(1),,所以或,所以,.
(2),,所以或,所以,.
(3),,,所以.
(4),,
所以或,所以,.
(5),,,所以或,所以,.
(6),,,,所以或,解得,.
2.解:设小圆形场地的半径为Rm,则大圆形场地的半径为(R+5)m.由题意,得,,.
因为,所以.
所以(舍去),.
答:小圆形场地的半径为m.
练习(第16页)
解:设原方程的两根为,.
(1)原方程可化为,所以,.
(2)原方程可化为,所以,.
(3)原方程可化为,所以,.
(4)原方程可化为,所以,.
习题21.2(第16页)
1.解:(1),移项,得,直接开平方,得,所以或,所以原方程的解是,.
(2),直接开平方,得,所以或,所以原方程的解是,.
(3),直接开平方,得,所以或,所以原方程的解是,.
(4),原方程可化为,直接开平方,得,所以或,所以原方程的解是,.
2.(1)9 3(2) (3)1 1(4)
3.解:(1),移项,得,配方,得,即,开平方,得,所以或,所以原方程的解为,.
(2),移项,得,配方,得,即,开平方,得,所以原方程的解为,.
(3),二次项系数化为1,得,移项,得,配方,得,即,开平方,得,所以或,所以原方程的解为或.
(4),二次项系数化为1,得,移项,得,配方,得,即,开平方,得,所以或,所以原方程的解为,.
4.解:(1)因为,所以原方程有两个不相等的实数根.
(2)因为,所以原方程有两个相等的实数根.
(3)因为,所以原方程没有实数根.
(4)原方程可化为.因为,所以原方程有两个不相等的实数根.
5.解:(1),因为,,,
所以,
所以,所以原方程的根为,.
(2),因为,,.
所以,所以
所以原方程的根为,.
(3),原方程化为,因为,,,所以,所以,所以原方程的根为,.
(4),原方程化为,因为,,,
所以,所以,
所以原方程的根为,.
(5),因为,,,
所以,所以,
所以原方程的根为,.
(6),因为,,,
所以,所以原方程无实数根
6.解:(1),原方程可化为,即,所以原方程的根为.
(2),原方程可化为,所以或,所以原方程的根为,.
(3),原方程可化为,所以或,所以原方程的根为,.
(4),原方程可化为,即,所以或,所以原方程的根为,.
7.解:设原方程的两根为,.
(1)原方程可化为.所以,.
(2),.
(3)原方程可化为,所以,.
(4)原方程可化为,所以,.
8.解:设这个直角三角形的较短直角边长为xcm,则较长直角边长为(x+5)cm,根据题意,得,即,解得,.因为直角三角形的边长为正数,所以不符合题意,舍去,所以.当时,,由勾股定理,得直角三角形的斜边长为.
答:斜边的长为cm.
9.解:设共有x家公司参加商品交易会,由题意,得,
所以,解得,.因为x必须是正整数,
所以不符合题意,舍去,所以.答:共有10家公司参加商品交易会
10.解:方法1(公式法):原方程可化为,因为,,,所以,所以,所以原方程的根为,.
方法2(因式分解法):原方程可化为,即,所以或,所以原方程的根为,.
11.解:设这个矩形的一边长为x m,则与其相邻的一边长为(10-x)m,根据题意,得,整理,得,解得,.当时,;当时,.故这个矩形相邻两边的长分别为6m和4m.
答:使得矩形相邻两边的长分别为4m和6m,即可围成一个面积为的矩形.
12.解:设这个凸多边形的边数为n,由题意可知,解得或.因为凸多边形的边数不能为负数,所以不合题意,舍去,所以.所以这个凸多边形是八边形.
假设存在有18条对角线的多边形,设其边数为x,由题意,得,解得.因为x的值必须是正整数,所以这个方程不存在符合题意的解故不存在有18条对角线
的凸多边形.
13.解:无论p取何值,方程总有两个不等的实数根理由如下:
原方程可以化为,
.
因为,所以,即,所以无论p取何值,原方程总有两个不等的实数根.
21.2.1 配方法
基础知识·细解读
知识点一 直接开平方法
1 直接开平方法的依据及实质
依据 实质
直接开平方法是解一元二次方程的最基本的方法,其依据是平方根的意义 解一元二次方程的基本思想是“降次”,通过“降次”把一元二次方程转化为一元一次方程.直接开平方法的实质就是把一个一元二次方程通过“降次”,转化为两个一元一次方程
2方程的根的情况
p的取值 方程的根的情况
有两个不相等的实数根,
有两个相等的实数根
没有实数根
【例1】用直接开平方法解下列方程:
(1); (2);
(3); (4).
解:(1)移项,得.
根据平方根的意义,得,即,.
(2)移项,得.二次项系数化为1,得.根据平方根的意义,得,即,.
(3)根据平方根的意义,得,即,.
(4)根据平方根的意义,得,即,.
知识点二 配方法
1 配方的目的和依据
目的 依据
降次,把一个一元二次方程转化成两个一元一次方程来解 完全平方公式:
2 用配方法解一元二次方程的一般步骤
示例 解题模板
【例2】用配方法解方程:.
特别提醒
(1)对于形如,的关于x的一元二次方程,可用直接开平方法求解.
(2)用直接开平方法解一元二次方程时,要把方程化成左边是含未知数的完全平方式,右边是非负数的形式,开方的结果要注意取正、负两种情况.
特别提醒
灵活运用整体思想,开方降次转化求解
对形如的关于x的一元二次方程,运用整体思想,把看作一个整体,直接开平方降次,得,即.
特别提醒
(1)不管用何种方法配方,方程左边一定要符合完全平方式的形式.
(2)当一元二次方程的二次项系数不为1时,一般先根据等式的性质,将二次项系数化为1,再配方求解.
特别提醒
配方时易出现的错误
(1)移项忘记变号.
(2)系数化为1时漏项.
(3)方程两边没有同时加上一次项系数一半的平方.
应用能力·巧提升
题型一 用配方法解一元二次方程
【例1】用配方法解方程:.
审题关键:根据配方法的步骤解方程.
破题思路:移项→二次项系数化为1→配方→直接开平方解方程
解:移项,得.
二次项系数化为1,得.
配方,得,
即.
由此可得,
所以,.
新思路
亦可先把二次项系数化为1,再移项.
方法技巧
抓住关键点,配方变简单
用配方法解一元二次方程的关键步骤是方程两边同时加上一次项系数一半的平方.抓住此关键点,配方显得更简单.
题型二 配方法的应用
【例2】用配方法求的最小值.
审题关键:求一个代数式的最值,可用配方法,但要注意代数式中的配方与解方程中的配方的不同之处.
破题思路:先提出二次项系数,再加上一次项系数一半的平方,最后减去一个同样的数,配成完全平方形式,利用完全平方式的非负性,可求代数式的最值.
解:
.
因为,
所以的最小值为0,
所以的最小值是.
一题多变
当y取何实数时,式子有最大值?最大值是多少?
解后反思
配方法求代数式最值,“两点注意”别忘掉
(1)先把二次三项式配方成的形式.
①当时,该二次三项式有最大值k;
②当时,该二次三项式有最小值k.
(2)因为要求代数式中的配方是恒等变形,所以在加上一次项系数一半的平方后,应减去一个同样的数,使代数式的值保持不变.
变式训练
1.用配方法解方程:
(1);
(2).
变式训练
2.当x取何实数时,式子有最小值?最小值是多少?
3.试用配方法证明的值恒小于0.
易误易混·精辨析
易错点一 把握不好配方法的某些关键步骤而出错
【例1】用配方法解方程:.
解:移项,得.
配方,得,
即.
直接开平方,得,2
即.
所以,.
防错警示
在配方时,易因只在方程左边加上一次项系数一半的平方而方程右边不加,导致方程的两边不相等,出现错误.
由平方根的意义开平方时,应该是正、负两种情况,不要漏掉其中一种.
易错点二 用配方法时,二次项系数没有化为1而致错
【例2】用配方法解方程:.
解:移项,得.
二次项系数化为1,得.
配方,得,即.
直接开平方,得.
所以,.
防错警示
用配方法解一元二次方程时,为了便于配方,需将二次项系数化为1,如果未将二次项系数化为1就进行配方,方程的两边还是加上一次项系数一半的平方,那么方程的左边不能配成完全平方式.
真题解密·探源头
中考真题 教材原型
(安徽中考·8分)解方程:. 解:配方,得,………2分 即.……………………………4分 开平方,得,…………………6分 所以,.…………8分 教材第9页练习第2题(1) 解方程:. 解:移项,得. 配方,得, 即. 开平方,得. 所以,.
命题人解密:教材习题很典型地考查了用配方法解一元二次方程,中考题就是针对一元二次方程的解法这一考点进行设置的,不同的是中考题不用移项,可以直接配方求解. 阅卷人解密:解答此类题时的两处失分点:(1)配方时,易忽视在方程的两边同时加上一次项系数一半的平方,只把方程的一边变形;(2)开平方时漏掉负值,只取正值.
高效训练·速提能
【基础达标】
1.已知一元二次方程可转化为两个一元一次方程,其中一个一元一次方程是,则另一个一元一次方程是()
A. B. C. D.
2.一元二次方程的根是()
A. , B. ,
C. D.
3.一元二次方程配方后可变形为()
A. B.
C. D.
4.若是完全平方式,则m的值为________.
5.解下列方程:
(1);
(2);
(3).
【能力提升】
6.若关于x的方程的左边可以写成一个完全平方式,则k的值为()
A.10 B.10或14 C.-10或14 D.10或一14
7.将方程化为的形式,其中m,n是常数,则________.
8.当________时,式子有最大值,最大值是________.
9.用两种方法解方程:.
10.证明:关于x的方程,无论m取何值,该方程都是一元二次方程.
【拓展创新】
11.在实数范围内定义运算“”,其法则为,求方程的根.
12.选取二次三项式中的两项,配成完全平方式的过程叫做配方.例如:
①选取二次项和一次项配方:;
②选取二次项和常数项配方:或;
③选取一次项和常数项配方:.
根据上述材料,解决下面的问题:
(1)写出的两种不同形式的配方;
(2)已知,求x的值.
21.2.2 公式法
基础知识·细解读
知识点一 一元二次方程根的判别式
1 根的判别式及其表示
(1)根的判别式:一元二次方程根的判别式是.
(2)表示:通常用希腊字母“”表示,即.
2 一元二次方程实数根的情况
的符号 方程实数根的情况
有两个不相等的实数根
有两个相等的实数根
无实数根
注意:(1)一元二次方程有实数根包括一元二次方程有两个不相等的实数根和有两个相等的实数根.此时,切勿丢掉等号.
(2)当一元二次方程有两个相等的实数根时,一般不说方程只有一个实数根.
(3)当a,c异号时,一元二次方程一定有两个不相等的实数根.
【例1】下列一元二次方程没有实数根的是()
A. B. C. D.
解析:A选项,,方程有两个相等的实数根;B选项,方程可化为,,方程没有实数根;C选项,方程有两个不相等的实数根;D选项,方程可化为,,方程有两个不相等的实数根.故选B.
答案:B
总结
判别式的作用大,与0的大小关系的应用别弄错
根据一元二次方程根的判别式与0的大小关系可以判断根的情况,反之根的情况也可反映根的判别式与0的大小关系.解决问题时要注意区分与0的大小关系是条件还是结论.
知识点二 一元二次方程的求根公式及公式法
1 一元二次方程的求根公式
对一元二次方程进行配方,可得到一元二次方程的求根公式:.
2 一元二次方程的求根公式的推导过程(配方法)
↓移项
↓二次项系数化为1
↓配方
,
即
↓开平方
,
即
注意:(1)一元二次方程的求根公式的应用条件是,且.
(2)用求根公式可求出任何有解的一元二次方程的根.
3 用公式法解一元二次方程的一般步骤
示例 解题模板
【例2】用公式法解方程:.
特别提醒
区分“方程有实数根”与“一元二次方程有实数根”
(1)“方程有实数根”中的方程可以是一元一次方程,还可以是其他方程,只要有实数根即可.
(2)“一元二次方程有实数根”隐含两个条件:二次项系数不为0,且判别式为非负数.
特别提醒
一元二次方程求根公式的推导过程中,在最后开平方时,,式子前面有双重符号“±”,所以无论还是,等式右边最终结果仍为.
特别提醒
用公式法解一元二次方程的两点注意
(1)一定要先把方程化为一般形式,再确定a,b,c的值,注意不要出现符号错误.
(2)先计算的值,再确定是否代入求根公式求解.
巧记口诀
要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数a,b,c,计算根的判别式.判别式值与零比,有无实根便可知.若有实根套公式,若无实根要告之.
应用能力·巧提升
题型一 一元二次方程根的判别式的应用
角度1 不解方程,判断方程根的情况
【例1】已知一次函数,且当时,y随x的增大而增大,则关于x的方程的根的情况是()
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
审题关键:本题首先要由已知判断方程是否为关于x的一元二次方程,再计算一元二次方程根的判别式,最后根据与0的大小关系确定一元二次方程根的情况.
解析:因为对于一次函数,当时,y随x的增大而增大,所以,所以,所以是关于x的一元二次方程,所以,所以方程有两个不相等的实数根,故选A.
答案:A
解后反思
应用判别式的两点注意
(1)判别式只适合一元二次方程,不适合其他方程.
(2)注意隐含条件,即二次项系数.
角度2 根据一元二次方程根的情况,确定字母的取值范围
【例2】(山东聊城中考)如果关于x的一元二次方程有两个不相等的实数根,那么k的取值范围是________.
审题关键:根据关于x的一元二次方程有两个不相等的实数根,可知.由此可以构造出关于k的不等式,要注意二次项系数不等于0.
解析:由方程有两个不相等的实数根,得,则有,解得.由方程是一元二次方程,得.所以,且.
答案:,且.
方法技巧
应用“”,列出不等式(组)
在利用根的判别式求待定字母的取值范围时,首先要根据方程的根的情况判断与0的大小关系,然后利用题目中的条件列出关于所求字母的不等式(组),最后求解.
角度3 应用根的判别式证明方程一定有实数根
【例3】(甘肃白银中考)已知关于x的方程.
(1)若此方程的一个根为1,求m的值;
(2)求证:不论m取何实数,此方程都有两个不相等的实数根.
审题关键:本题考查的是方程的根的定义及一元二次方程根的判别式,解题的关键是配方法的熟练应用.
破题思路:(1)把x=1代入方程即可得到一个关于m的一元一次方程,解该方程即可.
(2)要证明一元二次方程有两个不相等的实数根,只要证明该一元二次方程根的判别式恒为正数即可.
(1)解:把x=1代入方程,得,解得.
(2)证明:.
因为(,所以,
即,
所以不论m取何实数,此方程都有两个不相等的实数根.
一题多变
若此方程的一个根为2,求m的值,并求此时方程的另一个根
方法技巧
利用根的判别式证明一元二次方程有实数根的技巧
在利用根的判别式证明一元二次方程有实数根时,首先找到判别式,并将判别式配方,然后利用配方的结果判定根的判别式恒大于等于0,即可得证.
题型二 用公式法解一元二次方程
【例4】用公式法解一元二次方程:
(1);
(2).
审题关键:按照用公式法解一元二次方程的方法与步骤解方程.
破题思路:
把方程化为一般形式→确定a,b,c的值→算出的值→代入公式求解
解:(1)因为,,,
所以,
所以,所以,.
(2)将方程去分母后整理成一般形式,
得,
这里,,.
因为,
所以.
所以原方程的根是.
过程释疑:
原方程移项,得.两边同乘8,得.
因为,所以原方程有两个相等的实数根.
一题多变
你能解方程吗?
解后反思
用公式法解一元二次方程的两点注意
(1)用公式法解一元二次方程的关键是对a,b,c的确定.
(2)判断与0的大小关系是求解中的重要一步,是用求根公式解一元二次方程的前提条件.
题型三 解含字母系数的一元二次方程
【例5】解关于x的方程.
审题关键:关于x的方程是指x是未知数,m,n是已知数,注意二次项的系数含字母时,要考虑其是否为0.
破题思路:分和两种情况讨论.当时,转化为一元一次方程求解;当时,按照一元二次方程的求解方
法求解.
解:当,且,时,,原方程可化为,即.
因为,所以.
当,且,时,因为,,,
所以,
所以,不论m是正数,还是负数,都有,.
方法技巧
类比数字系数方程,巧解字母系数方程
解含有字母系数的方程的方法就是把字母看作已知常数,解题方法与步骤和系数为数字时相同,不同的是有时要对系数进行讨论:先判断二次项的系数是否为0,若为0,则按一元一次方程来求解;若不为0,再确定a,b,c的值,求出的值,当时,套用求根公式进行求解.
变式训练
1.下列方程中,没有实数根的是()
A.
B.
C.
D.
2.(山东潍坊中考)关于x的一元二次方程根的情况,下列说法正确的是()
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.无法确定
3.(广西桂林中考)若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是()
A.
B. ,且
C. ,且
D.
4.若关于x的一元二次方程有实数根,则k的取值范围是()
A. B. C. D.
5.已知关于x的一元二次方程.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
变式训练
6.用公式法解方程:
(1);
(2);
(3);
(4).
变式训练
7.解关于x的方程:
.
8.解关于x的方程:
(其中,).
易误易混·精辨析
易错点一 因考虑不全而出错
【例1】已知关于x的一元二次方程有两个实数根,求k的取值范围.
解:
.
因为原方程有两个实数根,
所以,
即,解得.
防错警示
本题易因错把方程“有两个实数根”看作“有两个不相等的实数根”,导致列出错误的不等式.在解答问题时只有认真审题,考虑全面,才能避免出现错误.
易错点二 因未讨论方程中字母系数的取值而出错
【例2】(辽宁锦州中考)若关于x的方程有实数根,则k的取值范围是________.
解析:当时,原方程可化为,解得;当时,原方程为一元二次方程,.令,解得.所以当时,原方程有实数根.
答案:
防错警示
当二次项系数含有字母时,若方程未指明是一元二次方程,不能直接利用一元二次方程根的判别式解题,要认真审题,当已知条件不明确时,应分类讨论.
真题解密·探源头
中考真题 教材原型
(湖南怀化中考)一元二次方程的根的情况为() A.有两个不相等的实数根 B.有两个相等的实数根 C.只有一个实数根 D.没有实数根 解析:由题意,得,所以 方程有两个不相等的实数根.故选A. 答案:A 教材第17页习题21.2第4题(4) 利用判别式判断方程的根的情况: . 解:原方程可化为. 因为, 所以方程有两个不相等的实数根.
命题人解密:教材习题考查了直接利用一元二次方程根的判别式判断方程根的情况,中考题也是针对这一知识点进行命题的,只是题型有所改变. 阅卷人解密:解答此类题时的主要失分点:易因弄错a,b,c的符号,导致计算的值时出错.
中考真题 教材原型
(四川成都中考·6分)已知关于x的方程没有实数根,求实数m的取值范围. 解:因为关于x的方程没有实数根, 所以,…………………2分 所以,………………4分 即,解得. 所以实数m的取值范围是.……6分 教材第17页习题21.2第13题 无论p取何值,方程总有两个不等的实数根吗?给出答案并说明理由. 解:方程总有两个不等的实数根.理由如下: 原方程可化为,.因为不论p取何值,均成立,所以,所以方程总有两个不等的实数根.
命题人解密:教材习题和中考题均是利用判别式解决问题的题目,不同的是教材习题考查了利用判别式恒大于0证明一元二次方程总有两个不等的实数根,中考题是已知一元二次方程有无实数根的情况来确定判别式与0的大小关系,进而确定字母的取值范围. 阅卷人解密:在解答此类题时,要注意正确计算判别式,合理地将判别式合并变形,以达到解决问题的目的.
高效训练·速提能
【基础达标】
1.下列关于x的一元二次方程中,没有实数根的方程是()
A. B. C. D.
2.一元二次方程的解是()
A. , B. , C. , D. ,
3.若关于x的方程的一个根为1,则m的值为()
A.1 B. C.1或 D.1或
4.(湖南长沙中考)若关于x的一元二次方程有两个不相等的实数根,则实数m的取值范围是________.
5.(湖南张家界中考)若关于x的一元二次方程无实数根,则实数k的取值范围是________.
6.解下列方程:(1);
(2).
7.已知关于x的方程有两个相等的实数根,求m的值.
【能力提升】
8.(河北中考)已知a,b,c为常数,且,则关于x的方程的根的情况是()
A.有两个相等的实数根
B.有两个不相等的实数根
C.无实数根
D.有一个根为0
9.若关于x的方程有实数根,则a满足()
A. B.,且 C.,且 D.
10.(山东枣庄中考)若关于x的一元二次方程有两个不相等的实数根,则一次函数的图象可能是()
11.已知关于x的方程.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以这两根为边长的直角三角形的周长.
【拓展创新】
12.(四川巴中中考)定义新运算:对于任意实数m,n,都有.等式右边是常用的加法、减法、乘法及乘方运算.例如,.根据上述知识解决问题:若的值小于0,请判断方程2 的根的情况.
21.2.3 因式分解法
基础知识·细解读
知识点一 因式分解法
1 因式分解法
描述 利用因式分解来解一元二次方程的方法
理论依据 若两个因式的积为0,则这两个因式至少有一个为0,即若,则或
实质 将一个一元二次方程降次,转化为两个一元一次方程
2 适合用因式分解法求解的一元二次方程的特点
方程一边为0,另一边易于分解成两个一次因式乘积的形式.
3 利用因式分解解一元二次方程的常用方法
(1)提公因式法:把多项式各项的公因式提到括号外面,将多项式写成因式乘积的形式.
(2)逆用平方差公式和完全平方公式来分解因式.
4 利用因式分解法解一元二次方程的一般步骤
示例 解题模板
【例】用因式分解法解方程:.
总结
两种常见的用因式分解法求解的方程
(1)解形如的一元二次方程时,将方程的左边运用提公因式法因式分解为,则或,即,.
(2)解形如的一元二次方程时,将方程的左边运用平方差公式因式分解为,则或,即,.
知识点二 灵活选用合适的方法解一元二次方程
求解一元二次方程的各种方法的特点及举例
方法 特点 举例
直接开平方法 解一元二次方程最简单的方法.若方程可化为 的形式,则宜选用直接开平方法求解 . 解:直接开平方,得 或, 所以,
配方法 解一元二次方程最基本的方法,它适用于解所有的一元二次方程.配方法要先配方,再降次.通过配方法可以推出求根公式 . 解:移项、配方,得. 开平方,得或, 所以,
公式法 解一元二次方程最通用的方法,它适用于解所有的一元二次方程.公式法是直接利用求根公式解方程 . 解:移项,得, 所以,,. 因为 ,所以, 所以,
因式分 解法 解一元二次方程较简单的方法.当方程的一边为0,另一边易化为两个一次因式的积时,就可优先选用因式分解法求解 . 解:移项,得. 因式分解,得. 于是得或, 所以,
特别提醒
(1)因式分解法只能解某些特殊的一元二次方程,不是所有的一元二次方程都能用因式分解法求解.
(2)用因式分解法解一元二次方程时,一定要把方程的右边化为0,否则会出现错误.
(3)用因式分解法解方程时,不要将方程两边同时除以含有未知数的式子,这样容易丢根.
巧记口诀
利用因式分解法解一元二次方程的12字口诀
右化零,左分解,
两因式,各求解.
拓展
解形如的一元二次方程时,将其左边因式分解,则方程化为,所以或,即,.
特别提醒
求解一元二次方程的方法的灵活选择
(1)直接开平方法只适用于一些特殊结构的一元二次方程.如,,等形式的方程.
(2)当一元二次方程的二次项系数为1,一次项系数为偶数时,用配方法比较简单.
(3)公式法是由配方法推导出来的,故能用公式法求解的一元二次方程一定可以用配方法来求解.
当解一个一元二次方程用其他方法都不简单时,可选用公式法.
(4)因式分解法只适用于方程一边等于0,另一边易于分解因式的一些特殊方程.
应用能力·巧提升
题型一 用因式分解法解一元二次方程
角度1 运用提公因式法分解因式解一元二次方程
【例1】用因式分解法解下列方程:
(1); (2)(甘肃兰州中考);
(3).
审题关键:用因式分解法解一元二次方程,一般先把方程移项整理化成右边为0的形式,观察方程的特点,通过变形,能提公因式的要提公因式.
破题思路:(1)移项变形,可提公因式x进行分解因式求解.(2)把原方程变形,可把y+2看作一个整体,提公因式进行因式分解求解.(3)把原方程变形,可把x-2看作一个整体,提公因式进行因式分解求解,注意符号变化.
解:(1)移项,得.因式分解,得.于是得或,解得,.
(2)将原方程变形为.移项,得.因式分解,得.于是得或,解得,.
(3)将原方程移项变形为.因式分解,得.
于是得或,
解得,.
新思路
此处也可把看作一个整体,把方程变形,提公因式进行因式分解来求解.
解后反思
在用因式分解法解一元二次方程时,千万不要急于把方程化成一般形式,要先观察方程的特点,能提公因式进行因式分解的就提公因式进行因式分解.如本例(3),把看作一个整体提公因式进行因式分解的方法比较简单.
角度2 运用平方差公式(或完全平方公式)分解因式解一元二次方程
【例2】用因式分解法解下列方程:
(1);
(2).
审题关键:观察方程特点,可用公式法分解因式的应先用公式法分解因式,再解方程.
破题思路:(1)可把写成,利用平方差公式分解因式求解.(2)先将移项、变号,再用平方差公式对因式分解,最后提公因式分解因式求解.
解:(1)原方程可化为.
因式分解,得.
整理,得,
于是得或,解得,.
(2)整理,得,
即.
因式分解,得,
即.
整理,得,
于是得或,所以,.
解后反思
分解因式时可以利用如,等式子,把互为相反数的两个代数式进行转换,进而可以运用公式较容易地找到公因式,使问题得解.
角度3 利用因式分解法解型的一元二次方程
【例3】用因式分解法解方程:.
审题关键:可利用进行因式分解.
破题思路:要设法找到两个数p,q,使,.
解:原方程可化为,
于是得或,
所以,.
方法技巧
利用因式分解法解型一元二次方程的技巧
形如的一元二次方程可尝试利用因式分解法求解,进行因式分解时,必须保证常数项拆成的两个因数的和为一次项系数,两个因数的积为常数项,另外两根的符号与拆成的两因数的符号正好分别相反.
题型二 用适当的方法解一元二次方程
【例4】选择适当的方法解下列方程:
(1);
(2);
(3);
(4).
审题关键:已知解一元二次方程的四种方法:直接开平方法、因式分解法、配方法和公式法.应根据方程特点,选择适当的方法求得方程的解.
破题思路:(1)先化为一般形式,根据方程的特点,可用公式法求解.(2)根据方程的特点,可先移项,用因式分解法求解,也可用直接开平方法求解.(3)先化为一般形式,根据方程的特点,可用因式分解法求解.(4)先化为一般形式,根据方程的特点,可用配方法求解.
解:(1)移项,得.
故,,,.
所以.
所以,.
(2)方法1:移项,得.
因式分解,得.
所以或.
所以,.
方法2:直接开平方,得,
所以,.
(3)原方程可化为,
即,所以.
(4)原方程可化为,
即.所以.所以,.
方法技巧
选择合适方法,轻巧求解一元二次方程
解一元二次方程要根据方程特点,合理变形,采用合适的方法.方法选择的一般顺序:直接开平方法→因式分解法→公式法→配方法.
变式训练
1.方程的解是()
A.
B.
C.,
D.,
2.解方程:
(1);
(2).
3.用因式分解法解方程:
.
4.(山西中考)解方程:
.
5.(辽宁沈阳中考)一元二次方程的根是()
A.,
B.,
C.,
D.,
6.解方程:
.
变式训练
7.选择适当的方法解下列方程:
(1);
(2);
(3);
(4).
易误易混·精辨析
易错点一 错用等式的性质
【例1】解方程:.
解:移项,得.所以.所以或.
所以,.
防错警示
本题易出现方程的两边同除以得的错误.这是因为当时,不符合等式的性质,因此,方程的两边不能同除以含未知数的式子.
易错点二 用因式分解法求解方程时,方程右边未化为0而出错
【例2】解方程:.
解:将方程整理,得.
因式分解,得.
所以或.
所以,.
防错警示
①用因式分解法解一元二次方程时,必须先使方程的右边为0才可将另一边的多项式分解因式求解.
真题解密·探源头
中考真题 教材原型
(四川巴中中考)解方程:. 解:移项,得. 整理,得. 所以或. 解得,. 教材第17页习题21.2第6题(3) 用因式分解法解方程: . 解:原方程可化为, 所以或, 所以,.
命题人解密:教材习题很典型地考查了用因式分解法解一元二次方程,中考题就是针对因式分解法解一元二次方程这一考点进行设置的,方程形式非常相近,解题方法也相同. 阅卷人解密:解答此类题时的两处失分点:(1)移项时忘记变号;(2)转化为两个一元一次方程时漏掉一个.
高效训练·速提能
【基础达标】
1.一元二次方程的解是()
A. B. C., D.,
2.方程的根为()
A. B. C., D.
3.解方程①;②;③时,解法选择较为恰当的是()
A.全部用公式法
B.①用直接开平方法,其余都用公式法
C.全部用配方法
D.分别用直接开平方法、公式法、因式分解法
4.(1)方程的解是________;
(2)方程的解是________.
5.用因式分解法解下列方程:
(1);
(2);
(3).
6.先阅读材料,再解答问题.
小聪和小明在解一元二次方程时,采用了不同的方法.
小聪:移项,得.
直接开平方,得.
解得,.
小明:将原方程变形,得.
整理,得________________.
所以或.
所以,.
小聪和小明解方程分别运用的什么方法?横线上应填什么?
【能力提升】
7.(青海中考)已知等腰三角形的腰和底的长分别是一元二次方程的根,则该三角形的周长为()
A.8 B.10 C.8或10 D.12
8.已知关于x的一元二次方程的一个实数根为1,那么它的另一个实数根是()
A.-2 B.0 C.1 D.2
9.设a,b为方程的两根,,则的值为________.
10.用适当的方法解下列方程:
(1);(2);
(3);(4).
11.(一题多解)至少用两种方法解方程:.
【拓展创新】
12.定义新运算“”如下:当时,;当时,.若,则x的值是________.
13.探究下表中的奥秘,并完成填空:
一元二次方程 两个根 二次三项式因式分解
,
,
,
,
______, ______
将你发现的结论一般化,并写出来.
*21.2.4一元二次方程的根与系数的关系
基础知识·细解读
知识点一 元二次方程的根与系数的关系
方程的根与系数的关系
数学语言 设的两个根为,,则,
文字语言 一元二次方程的两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比
使用条件 (1)方程是一元二次方程,即二次项系数; (2)方程有实数根,即
重要推论 设一元二次方程的两根为,, 则,
常见变形 (1); (2); (3); (4); (5); (6)
【例】根据一元二次方程的根与系数的关系,求下列方程的两根,的和与积.
(1);(2);(3).
解:(1),.
(2)整理,得,
所以,.
(3),.
总结
利用一元二次方程的根与系数的关系求两根的和与积的两点注意
(1)一元二次方程必须有两个实数根().
(2)中的负号与方程中a,b的符号不要混淆.
拓展
利用一元二次方程的根与系数的关系进一步讨论根的符号
设一元二次方程的两根为,,则
,且 两根同为正数
两根同为负数
,且 两根异号且正根的绝对值较大
两根异号且负根的绝对值较大
应用能力·巧提升
题型一 一元二次方程根与系数关系的应用
角度1 已知一个根,利用根与系数的关系求另一个根
【例1】(山东潍坊中考改编)已知关于x的方程有一个根是,求另一个根.
审题关键:本题考查了一元二次方程的根与系数的关系及根的定义,解题的关键是记住一元二次方程的根与系数的关系及熟练掌握一元二次方程的解法,并能灵活运用.
破题思路:思路1:利用根与系数的关系直接列出关于另一个根的方程号求解即可;思路2:先把代入原方程,求得m的值,再解方程求出另一个根.
解:方法1:设方程的另一个根是,由一元二次方程的根与系数的关系,得,解得.
所以方程的另一个根是-4.
方法2:把代入原方程,得,解得.
所以原方程为,解得,.
所以方程的另一个根是-4.
方法技巧
已知一元二次方程的一个根,求另一个根的方法
(1)方法1(利用根与系数的关系):当方程的二次项系数、一次项系数已知,常数项未知时,利用两根的和求另一个根;当方程的二次项系数、常数项已知,一次项系数未知时,利用两根的积求另一个根
(2)方法2(利用根的定义):先把方程的已知根代入方程求出未知系数或常数项,再解方程求另一个根.
角度2 利用根与系数的关系求某些代数式的值
【例2】(山东德州中考)若方程的两根为,,则________.
审题关键:本题求解的关键是利用根与系数的关系,,将所求的代数式变形为含和的式子.
解析:因为方程的两根为,,所以,,所以.
答案:
方法技巧
巧用根与系数的关系,求特殊代数式的值
算→计算出,的值
↓
变→将所求的代数式变形为用和表示的式子
↓
代→代入所求的代数式计算
角度3 利用根与系数的关系确定待定字母的值
【例3】(湖北鄂州中考)已知关于x的一元二次方程有两个不等实根,.
(1)求实数k的取值范围;
(2)若方程两实根,满足,求k的值.
审题关键:根据判别式的符号可求得k的取值范围;由,可考虑利用一元二次方程的根与系数的关系求解.
破题思路:(1)由于方程有两个不等实根,故其根的判别式,列不等式可确定实数k的取值范围.(2)先讨论两根的符号,再去掉中的绝对值符号,最后根据根与系数的关系,可得关于k的一元二次方程,求得k的值.
解:(1)因为原方程有两个不相等的实数根,所以
,解得
(2)因为,所以.
因为,所以,.
所以.
因为,所以.
所以或.因为,所以.
解后反思
使用根与系数的关系的前提——
利用一元二次方程根与系数的关系求方程的系数时,千万不要忘记将系数代回验证是否成立,因为根与系数的关系是在一元二次方程中的前提下使用的.
题型二 已知两数的和与积,构造一元二次方程解决问题
【例4】已知两个数的和是8,积为15,求这两个数.
审题关键:可利用一元二次方程的根与系数的关系,根据两个数的和与积构造一元二次方程求这两个数.
破题思路:根据一元二次方程的根与系数的关系,可用一8作为一次项系数,15作为常数项,构造一个二次项系数是1的一元二次方程,则这个一元二次方程的根就是所要求的两个数.
解:根据一元二次方程的根与系数的关系,知要求的两个数是方程的两个根,解这个方程得,.所以这两个数是3,5.
方法技巧
已知两数和与积,巧构一元二次方程求两数
把已知两个数的和与积分别看成一元二次方程两个根的和与积,则可根据“方程能化为”构造一个符合要求的一元二次方程来求这两个数.
变式训练
1.(山东枣庄中考)已知关于x的方程有一个根为-2,则另一个根为()
A.5 B.-1 C.2 D.-5
2.若是关于x的方程的一个根,试求方程的另一个根.
3.已知m,n是方程的两个实数根,则的值为()
A.-1 B. C. D.1
4.(广西玉林中考)若关于x的一元二次方程有两个实数根,,则()
A. B. C.4 D.-4
5.已知关于x的一元二次方程.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根为,,且满足,求实数m的值.
变式训练
6.已知实数,满足,,则以,为根的一元二次方程是()
A.
B.
C.
D.
易误易混·精辨析
易错点一 用根与系数的关系解题时,忽视对判别式的检验而致错
【例1】已知关于x的方程,下列说法正确的是()
A.若两根是,,则
B.若两根是,,则
C.若两根是,,则
D.以上说法都不对
解析:因为,
所以方程没有实数根.
故选D.
答案:D
防错警示
本题易因忽视一元二次方程的根与系数的关系使用的前提条件,而错选A或C.使用一元二次方程的根与系数的关系解题时,要注意检验是否成立.
易错点二 忽视题干中的隐含条件而致错
【例2】已知关于x的方程的两个根互为相反数,求k的值.
解:由题意可知,,即,
解得.
由于,
当时,,不合题意,舍去;
当时,,
又因为,符合题意.
所以.
防错警示
应用一元二次方程的根与系数的关系解题时,要关注已知中的隐含条件.本题易因未检验方程的判别式及忽视与互为相反数,未舍去不合题意的而出错.
真题解密·探源头
中考真题 教材原型
(四川凉山州中考)已知,是一元二次方程的两根,则的值是 A. B. C. D. 解析:把一元二次方程化为一般形式为,于是,,因此 .故选D. 答案:D 教材第16页练习(1) 不解方程,求方程两个根的和与积: . 解:设方程的两个根为和. 移项,得. 根据根与系数的关系,得, .
命题人解密:教材习题考查了直接利用一元二次方程的根与系数的关系求两根的和与积.中考题是针对一元二次方程的根与系数的关系,求与两根的和与积有关的简单代数式的值,难度稍高于教材习题. 阅卷人解密:在解答此类题时的两处失分点:(1)易弄错两根的和或积的符号;(2)易把代数式变形错误
高效训练·速提能
【基础达标】
1.(湖北黄冈中考)若方程的两个实数根分别为,,则()
A.-4 B.3 C. D.
2.(江西中考)设,是一元二次方程的两个根,则的值是()
A.2 B.1 C.-2 D.-1
3.(浙江金华中考)一元二次方程的两根为,,则下列结论正确的是()
A. , B. , C. D.
4.(山东威海中考)已知,是关于x的方程的两实数根,且,则的值是()
A. B. C.4 D.-1
5.(湖北黄石中考)若关于x的一元二次方程的两实数根之积为负数,则实数m的取值范围是________.
6.(湖北恩施州中考)已知一元二次方程的两根为m,n,则________.
7.已知两个数的和是10,积为21,求这两个数.
【能力提升】
8.(山东烟台中考)若,是一元二次方程的两个根,则的值为()
A.-1 B.0 C.2 D.3
9.已知关于x的一元二次方程的两个实数根为,,若,则m的值为________.
10.如果m,n是两个不相等的实数,且满足,,那么代数式________.
11.已知关于x的方程.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)当该方程的一个根为1时,求a的值及方程的另一根.
【拓展创新】
12.关于x的方程有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使方程的两个实数根的倒数
和等于0?若存在,求出k的值;若不存在,说明理由.
本书参考答案
21.2 解一元二次方程
21.2.1 配方法
应用能力·巧提升
1.解:(1)移项,得.配方,得,即.由此可得,所以,.
(2)二次项系数化为1,得.移项、配方,得,即,所以.
所以,.
【例2】一题多变
解:
.
因为,所以的最大值为0,所以当时,原代数式有最大值,最大值是.
2.解:因为可配方为,无论x取何实数,,所以当时,有最小值1.
3.证明:
.
因为
所以,
所以.
因此,的值恒小于0.
高效训练·速提能
1.D 解析:,直接开平方,得,则或.故选D.
2.D 解析:原方程可变形为.根据平
方根的意义,得.故选D.
3.A 解析:移项,得.配方,得,即.故选A.
4. 解析:根据完全平方式的结构特征,知,所以.
5.解:(1)原方程可化为.开平方,得,所以,.
(2)二次项系数化为1,得,即.开平方,得.所以,.
(3)移项,得.
配方,得,即.
开平方,得或,所以,.
6.D 解析:方程的左边变形为,所以,即或,解得或.故选D.
7.55 解析:将移项,得.配方,得,即,所以,,所以.
8.4 21 解析:.
当时,有最大值21.
9.解:方法1(配方法):展开,得.
移项、合并同类项,得.
二次项系数化为1,得.
配方,得.
直接开平方,得,
所以,.
方法2(直接开平方法):原方程可化为.
直接开平方,得或,解得,.
10.证明:二次项系数.
因为,所以,
即.
所以无论m取何值,该方程都是一元二次方程
11.解:因为,
所以.
所以.所以.
所以,即,.
12.解:(1)
.
(2)因为,
所以,
所以,,
所以,,所以.
21.2.2 公式法
应用能力·巧提升
1.B 解析:方程的根的判别式等于,所以方程没有实数根.
2.A 解析:
,
因为,即,
所以方程有两个不相等的实数根,故选A.
3.B 解析:因为关于x的一元二次方程(有两个不相等的实数根,所以
即所以,且.
故选B
4.D 解析:因为一元二次方程有实数根,所以,解得.故选D.
【例3】一题多变
解:把代入方程,得,解得.
所以原方程为,
即.
解得,.
所以此时方程的另一个根是.
5.(1)证明:原方程可化为,
所以.
因为,所以,即.
所以对于任意实数m,方程总有两个不相等的实数根.
(2)解:把代入原方程得.解得
.所以原方程可化为.解得
,.所以方程的另一个根是4.
【例4】一题多变
解:因为,,,所以,所以方程没有实数根.
6.解:(1)因为,,,
所以.
所以,
所以,.
(2)方程化为.
因为,,,
所以,
所以,
所以.
(3)方程化为.
因为,,,
所以,
所以原方程无实数根,
(4)方程化为3.
因为,,,
所以,
所以,
所以,.
7.解:①当,即时,原方程化为,所以.
②当,即时,.
当,即,且时,方程有两个不相等的实数根,
,;
当时,方程有两个相等的实数根,
;
当时,方程没有实数根.
8.解:将原方程化为一般形式为.
因为,,,
所以
,
所以,
所以,.
高效训练·速提能
1.C 2.A
3.D 解析:把代入方程可得,所以,
,所以,
即,故选D.
4. 解析:由题意,得,解得.
5. 解析:因为关于x的一元二次方程无实数根,所以.因为,,,
所以,即.所以.
6.解:(1)方法1:移项,得.
配方,得,即,
由此可得,
即,.
方法2:因为,,,
所以.
所以,
所以,.
(2)原方程可化为,
所以,,,
所以,
所以,
所以,.
7.解:因为关于x的方程有两个相等的实数根,
所以.
所以.
所以,.
8.B 解析:因为,即,
所以,,.所以关于x的方程是一元二次方程,且,
故该方程有两个不相等的实数根.当方程有一个根为0时,将代入方程,得,这与矛盾,D项错误.故选B.
9.A 解析:当时,有实数解,此时;当时,应满足,解得.综上所述,
.故选A
10.B 解析:因为关于x的一元二次方程有两个不相等的实数根,所以,即,所以.所以k,b异号,选项A中,,,所以选项A错误;选项B中,,.所以选项B正确:选项C中...所以选项C错误;选项D中,,所以选项D错误,故选B
11.(1)证明:
.
因为,所以,所以方程恒有两个不相等的实数根.
(2)解:把代入方程,得,所以方程为,解得,.
所以方程的另一个根是3.
①当1和3都是直角三角形的直角边长时,由勾股定理,知斜边长为,所以直角三角形的周长为;
②当3为直角三角形的斜边长时,由勾股定理,知另一条直角边长为,所以直角三角形的周长为.
综合①②,知以这两根为边长的直角三角形的周长为或.
12.解:由定义新运算的法则,知.
2☆a的值小于0,即,解得.
方程的根的判别式.
因为,,所以,所以,故方程有两个不相等的实数根.
21.2.3 因式分解法
应用能力·巧提升
1.D 解析:因为,
所以,
所以,
所以,.
2.解:(1)移项,得.
因式分解,得.
于是得或,
解得,.
(2)移项,得.
因式分解,得.
于是得或,
解得,.
3.解:移项,得,
即.
因式分解,得.
整理,得,于是得或,解得,.
4.解:原方程可化为.
移项,得.
提公因式,得.
整理,得.
所以或.
所以,.
5.B 解析:方程整理,得.因式分解,得.解得,.故选B
6.解:原方程可化为,
因式分解,得.
解得,.
7.解:(1),由求根公式,
得.
所以,.
(2)直接开平方,得.
所以,.
(3)移项,得.
因式分解,得.
于是得或.
所以,.
(4)配方,得.所以.
所以,.
高效训练·速提能
1.C 解析:原方程为,所以或,所以,.故选C.
2.C 解析:方程整理,得.所以.解得,.
3.D 解析:根据方程的特征可知选D.
4.(1), 解析:由因式分解法可将原方程化为.所以或.所以,.
(2), 解析:原方程可化为.所以或.
解得,.
5.解:(1)因式分解,得.
整理,得.所以或.所以,.
(2)因式分解,得.于是有或.所以,.
(3)因式分解,得.
整理,得.所以或.
所以,.
6.解:由小聪将方程先移项再开平方,知他用的是直接开平方法;
小明将方程分解为两个因式的乘积,他用的是因式
分解法.故应填.
7.B 解析:因为,所以,,故三角形三边长可能为2,2,4或2,4,4,但由于,所以2,2,4不能构成三角形,所以该三角形的周长为.
8.A 解析:因为关于x的一元二次方程的一个实数根为1,所以把代入一元二次方程,得,解得.所以原方程为,所以,所以,.故选A.
9.-6 解析:原方程变形,得.因式分解,得.所以,.因为,所以,,故.
10.解:(1)方程整理,得.
所以,所以,.
(2)因为,,,
所以,
所以,
所以,.
(3)方程整理,得,
即.
所以或,
所以,.
(4)移项,得.
配方,得,
即.
所以,所以,.
11.解:方法1(配方法):配方,得
,
即,所以,
所以,.
方法2(公式法):整理,得,
因为,,,
所以,
所以,
所以,.
方法3(因式分解法):整理,得.
分解因式,得,
所以或,
所以,.
12.-1或 解析:若,即,根据定义,得
,解得,,这两个解均符合题意;若,即,根据定义,得,解得,,这两个解均不符合题意.综上所述,,.
13.解:依次填:,-3,,3.
发现的结论:若一元二次方程的
两个根为,,则.
21.2.4 一元二次方程的根与系数的关系
应用能力·巧提升
1.B 解析:方法1:设另一个根为x1.因为关于x的方程有一个根为-2,所以,解得,所以另一个根为-1.故选B.
方法2:把代入方程,得,解得,所以原方程为,解得,.故选B.
2.解:方法1:因为关于x的方程有一个根,所以,所以.
方法2:把代入方程,得,解得,所以原方程为,解得,.
3.A 解析:因为m,n是方程的两个实数根,所以,,所以.故选A.
4.D 解析:因为,,
所以.故选D.
5.解:(1)因为方程有实数根,所以,所以.
(2)因为方程的两实数根为,,所以.①
又因为,②
联立①②并解方程组,得
所以.
6.A 解析:以,为根的一元二次方程是,所以满足条件的是.
高效训练·速提能
1.D 解析:因为方程的两个实数根分别为,,,,所以.故选D.
2.D 解析:.故选D.
3.C 解析:将代入,得,所以不是方程的根,故A选项错误;将代入,得,所以不是方程的根,故B选项错误;由一元二次方程的根与系数的关系,得,,故C选项正确,D选项错误.故选C.
4.A 解析:由根与系数的关系,得,,所以,,所以,,所以的值是.故选A.
5. 解析;设,为方程的两个实数根,由已知,得,即,解得.
6. 解析:由题意,得,由一元二次方程根与系数的关系,得,,所以.
7.解:根据根与系数的关系,知两个数是方程的两个根,解这个方程,得,
.所以这两个数是3,7.
8.D 解析:因为,是一元二次方程的两个根,所以,,所以.故选D.
9.2或-6 解析:根据题意,得,.又因为,
所以,解得,,并且当或-6时方程都有解,所以m的值为2或-6.
10.2032 解析:由题意可知,m,n是的两个不相等的实数根.根据根与系数的关系,知..又因为,
所以
.
11.解:(1)根据题意,得0,解得.
(2)方法1:设原方程的另一根为,由根与系数的关系,得
解得
所以a的值是-1,原方程的另一根为-3.
方法2:把代入原方程,得,解得,所以原方程为,解得,.
所以,原方程的另一根为-3.
12.解:(1)根据题意,得,所以.又因为,所以k的取值范围是,且.
(2)不存在符合条件的实数k,理由如下:
假设存在符合条件的实数k,设方程的两根分别为,,由根与系数的关系,得,.因为,所以,所以.
由(1),知当时,,原方程无实数根.
所以不存在符合条件的实数k.
教材参考答案
21.2 解一元二次方程
练习(第6页)
解:(1),所以,所以,.
(2),移项,得,,所以,.
(3),移项,得
所以,所以,.
(4),移项,整理,得,
所以,所以,.
(5)可化为,
所以,所以,.
(6),移项,得,所以,所以.
因为,所以原方程无实数根.
问题(第7页)
两边加9,可以将方程左边配成完全平方形式,若加其他数则不行
练习(第9页)
1.(1)25 5(2)36 6(3) (4)
2解:(1),,,,
故,.
(2),,,,
故,.
(3),,,,,,故,.
(4),,,,
所以,.
(5),,,故原方程无实数根.
(6),,,,故,.
练习(第12页)
1.解:(1),因为,,,
所以,
所以,所以,.
(2),因为,,,
所以,所以.
所以,.
(3),因为,,,
所以,所以,
所以,.
(4),因为,,,所以,所以,所以,.
(5),整理,得,
因为,,,
所以,所以,
所以,.(当得出时,也可移项后,直接开平方得结果)
(6),整理,得,因为,,,
所以,
所以,所以,.
2.解:,因为,,,
所以,所以,所以,(不符合题意,舍去).
答:铁皮各角应切去边长为5cm的正方形.
练习(第14页)
1.解:(1),,所以或,所以,.
(2),,所以或,所以,.
(3),,,所以.
(4),,
所以或,所以,.
(5),,,所以或,所以,.
(6),,,,所以或,解得,.
2.解:设小圆形场地的半径为Rm,则大圆形场地的半径为(R+5)m.由题意,得,,.
因为,所以.
所以(舍去),.
答:小圆形场地的半径为m.
练习(第16页)
解:设原方程的两根为,.
(1)原方程可化为,所以,.
(2)原方程可化为,所以,.
(3)原方程可化为,所以,.
(4)原方程可化为,所以,.
习题21.2(第16页)
1.解:(1),移项,得,直接开平方,得,所以或,所以原方程的解是,.
(2),直接开平方,得,所以或,所以原方程的解是,.
(3),直接开平方,得,所以或,所以原方程的解是,.
(4),原方程可化为,直接开平方,得,所以或,所以原方程的解是,.
2.(1)9 3(2) (3)1 1(4)
3.解:(1),移项,得,配方,得,即,开平方,得,所以或,所以原方程的解为,.
(2),移项,得,配方,得,即,开平方,得,所以原方程的解为,.
(3),二次项系数化为1,得,移项,得,配方,得,即,开平方,得,所以或,所以原方程的解为或.
(4),二次项系数化为1,得,移项,得,配方,得,即,开平方,得,所以或,所以原方程的解为,.
4.解:(1)因为,所以原方程有两个不相等的实数根.
(2)因为,所以原方程有两个相等的实数根.
(3)因为,所以原方程没有实数根.
(4)原方程可化为.因为,所以原方程有两个不相等的实数根.
5.解:(1),因为,,,
所以,
所以,所以原方程的根为,.
(2),因为,,.
所以,所以
所以原方程的根为,.
(3),原方程化为,因为,,,所以,所以,所以原方程的根为,.
(4),原方程化为,因为,,,
所以,所以,
所以原方程的根为,.
(5),因为,,,
所以,所以,
所以原方程的根为,.
(6),因为,,,
所以,所以原方程无实数根
6.解:(1),原方程可化为,即,所以原方程的根为.
(2),原方程可化为,所以或,所以原方程的根为,.
(3),原方程可化为,所以或,所以原方程的根为,.
(4),原方程可化为,即,所以或,所以原方程的根为,.
7.解:设原方程的两根为,.
(1)原方程可化为.所以,.
(2),.
(3)原方程可化为,所以,.
(4)原方程可化为,所以,.
8.解:设这个直角三角形的较短直角边长为xcm,则较长直角边长为(x+5)cm,根据题意,得,即,解得,.因为直角三角形的边长为正数,所以不符合题意,舍去,所以.当时,,由勾股定理,得直角三角形的斜边长为.
答:斜边的长为cm.
9.解:设共有x家公司参加商品交易会,由题意,得,
所以,解得,.因为x必须是正整数,
所以不符合题意,舍去,所以.答:共有10家公司参加商品交易会
10.解:方法1(公式法):原方程可化为,因为,,,所以,所以,所以原方程的根为,.
方法2(因式分解法):原方程可化为,即,所以或,所以原方程的根为,.
11.解:设这个矩形的一边长为x m,则与其相邻的一边长为(10-x)m,根据题意,得,整理,得,解得,.当时,;当时,.故这个矩形相邻两边的长分别为6m和4m.
答:使得矩形相邻两边的长分别为4m和6m,即可围成一个面积为的矩形.
12.解:设这个凸多边形的边数为n,由题意可知,解得或.因为凸多边形的边数不能为负数,所以不合题意,舍去,所以.所以这个凸多边形是八边形.
假设存在有18条对角线的多边形,设其边数为x,由题意,得,解得.因为x的值必须是正整数,所以这个方程不存在符合题意的解故不存在有18条对角线
的凸多边形.
13.解:无论p取何值,方程总有两个不等的实数根理由如下:
原方程可以化为,
.
因为,所以,即,所以无论p取何值,原方程总有两个不等的实数根.
同课章节目录
